超声波测距信号小波阈值去噪参数的选定方法*

陈文会,丁晓鸿,陈江宁,刘小民

(1.西北工业大学电子信息学院,西安 710129;2.陕西脉航交通测控有限公司,西安 710061)



超声波测距信号小波阈值去噪参数的选定方法*

陈文会1*,丁晓鸿1,陈江宁2,刘小民2

(1.西北工业大学电子信息学院,西安 710129;2.陕西脉航交通测控有限公司,西安 710061)

讨论了超声波测距信号小波阈值去噪参数的选定方法和最优选取原则。在超声波测距回波信号中加入10 dB的噪声信号,在MATLAB仿真环境下,用硬阈值函数、软阈值函数、半软阈值函数,分别对超声波回波信号进行处理,通过实验分析得出,在选取2层分解、消失矩阶数为5时,选择Sym7小波基、半软阈值函数降噪时,信号SNR改善较大,为5.35 dB,RMSE最小,为0.094 dB,说明在有效去除信号噪声的同时,重构后的失真最小。

超声回波信号;小波去噪;参数选定

在非接触测量方式中,超声波测距因其传播速度慢、纵向分辨率强、测距精度高及不易受干扰等优良特点,应用领域广泛。超声波在介质中传播时其振幅会产生衰减,衰减程度随着频率和距离的增大而增大,信号信噪比也会越来越低。利用超声波信号测距时,为了得到精确的测量结果,必须对超声波信号进行去噪处理。硬件上超声去噪方法是将信号通过一个低通或带通滤波器,但是在噪声污染严重的环境、探测远距离的目标时,信号信噪比很低,采用滤波器进行滤波,不仅信噪比得不到改善,信号的有用信息也有可能被模糊化,导致信号有用信息的丢失而产生失真,从而影响回波时间的测量准确度和精度。本论文针对超声波测距回波信号中存在噪声的问题,采用小波阈值法进行去噪。根据超声波信号特点,讨论了小波阈值去噪的步骤和核心参数的选取原则,通过研究小波阈值去噪法在超声波信号中的实际降噪效果,分析得出适合于超声波信号的小波降噪参数[1]。

目前,信号去噪的方法很多,比如传统的Fourier变换去噪、Wiener滤波、Kalman滤波、时间序列分析、同态滤波、中值滤波、小波变换等方法。但是,传统的Fourier变换去噪只能用于信号和噪声频带重叠非常小或者是完全分开的情况,通过滤波器将有用信号和噪声分开,实际中信号谱和噪声谱是任意重叠的,用此方法不能达到理想的去噪效果[2];Wiener滤波器是一种频域分析方法,缺点是要求信号是一维平稳随机过程,要求求解Wiener-Hopf方程和存储全部历史数据,计算量和存储量大,不便于实时应用;Kalman滤波器缺点是要求模型参数和噪声统计是精确已知的,如果采用不精确的模型设计,Kalman滤波器会导致滤波发散;时间序列分析方法是以白噪声估计理论为基础,以ARMA信息模型作为最优滤波工具,虽然计算量小,但仅适用于处理时不变系统[3];同态滤波和中值滤波多用于图像处理领域[4]。

因此,传统的去噪方法已经不能满足现代数字信号处理中对信号去噪效果的要求。小波变换因时域、频域方面的优越性以及多分辨率的特性,应用前景广阔,降噪效果比采用传统方法好[5]。

小波去噪的方法主要有4种[5]:(1)小波分解与重构去噪。适用于有用信号和噪声的频带相互分离的情况;(2)平移不变量小波去噪。适用于信号中混有白噪声且含有若干不连续点的情况;(3)小波变换模极大值法去噪。适用于信号中混有白噪声且含有较多奇异点的情况;(4)小波阈值法去噪。适用于信号中混有白噪声的情况,使用这种方法,几乎可以完全抑制噪声,且很好地保存原始信号的特征峰值点。

1 小波阈值去噪的基本步骤

小波阈值去噪法的基本原理是:系统设置固定的临界阈值,当小波的系数小于它的时候,将有关联的小波系数设置成0;其他情况时,将有关联的小波系数予以保留或者按照某个规律收缩,最后利用处理后的小波系数进行小波重构得到去噪信号。

设一夹有噪声的信号表达式为:

x(i)=s(i)+n(i)

(1)

式中:中i=0,1,…,N-1,x(i)为含噪信号,s(i)为有用信号,n(i)为噪声。

小波阈值法去噪的基本步骤是[6]:

第1步 筛选恰当的小波基。Dbn、Symn和Coifn都是比较常用的小波基,其中n是小波基的消失矩,要根据具体情况给N赋予恰当的值。

第2步 选择分解层数J。分解的层数J确定下来后,利用式(2)对信号做正交小波变换,得到各层的尺度系数cj,k和小波系数dj,k。设含噪信号的初值为x(i)=c0,k。

(2)

式中:k=0,1,…,N-1,j=0,1,…,J,J为分解层数,N为信号采样点数,h和g互为正交滤波器组。

第3步 选取合适的阈值和阈值函数。由于尺度系数一般为低频有用信号,而小波系数一般为高频噪声信号,通过选定合理的阈值函数和阈值,量化处理各层小波系数dj,k,不改变尺度系数cj,k的值。

第4步 重新构造信号。根据式(3),选用新的小波系数重构信号,重构后的信号就是去噪后的信号。

(3)

根据以上基本步骤可知,影响小波阈值去噪效果的4个核心因素是:小波基(包含消失矩)、分解层数J、阈值函数及阈值。只有根据信号的特点,合理的选取以上影响因素,才能取得理想的去噪效果。

2 小波去噪效果评价指标

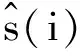
(4)

(5)

SNR反映了信号和噪声之间的能量比,SNR越大,表明具有更好地去噪效果;RMSE表示原始信号与去噪后信号两者之间的差别情况,如果均方误差得到缩小,表示重构后的信号失真较小,去噪效果有显著的提高。

3 小波阈值去噪参数的选定

小波阈值去噪的参数选择会随着信号的不同而变化,由于信号不同,其具有的噪声强度也不同,对阈值的选定也是不尽相同的,选择合理的参数既能够达到更好的降噪效果,去除信号噪声,又能够保证重构的信号不丢失原始信号的信息。

通过仿真实验,对理想的超声波回波信号加信噪比为10dB的噪声后,选用合适的参数进行去噪,并分析对比选择不同参数对超声波去噪带来的影响,为实际回波信号的处理提供依据。

3.1 超声回波信号模型的建立

一般地,理想状态下的回波信号为纯净信号,混有噪声的信号为加噪信号。根据超声波波动方程

式中:h、φ为超声换能器参数;f为超声波频率;m为不同介质条件下的取值(1～3)。

选用发射频率f为40kHz的T/R40-16型超声波传感器,设计一个采样频率为480kHz的超声波测距系统,测量一个2米远的目标,由此得到的回波信号作为理想条件下的超声波信号[8],如图1(a)。对理想信号加信噪比为10dB的高斯白噪声,做归一化处理后的波形如图1(b)所示。

从图1看出,加噪声后的信号波形失真严重。

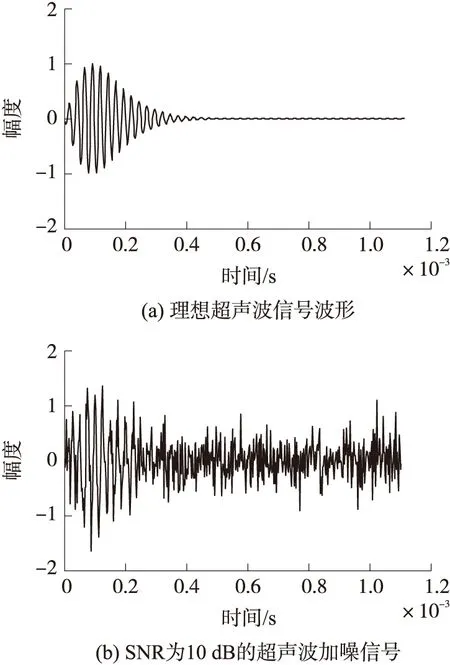
图1 理想超声波信号和SNR为10 dB的超声波加噪信号波形

3.2 分解层数的选取

理论上,小波分解的最大分解层数为J=⎣log2N」,⎣ 」代表向下取最近邻的整数。分解层数越大,噪声和信号的不匹配特征就越明显,这样就更加容易进行信号和噪声的分离[9-10],但重构与分解层数呈正相关性,分解层数越多,重构后的失真就越大,重构误差也随之增大。所以,不是J越大越好,要根据信号的具体特点选择合适的分解层数。

当SNR较大时,噪声比较小,则J稍微小一点即可把噪声分离出去;当SNR较小时,噪声干扰比较严重,则J要取大一点才能有效的区分噪声和信号,从而抑制噪声。因此,J的选取一般取决于SNR的大小,一般而言,SNR<=20dB,取J的取值范围为2层～4层,在同一条件下,对超声信号进行层数分解后重构观察波形,分解2层时,重构信号与理想超声信号最接近,失真最小。

图2是分解层数为2和3时的超声波加噪信号的波形。

图2 不同分解层数下的超声波加噪信号

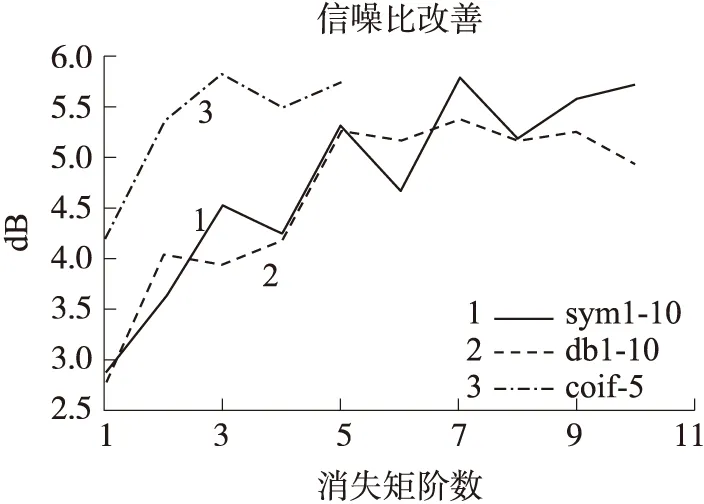
图3 不同小波基去噪后的SNR改善效果

3.3 小波基的选取

图3和图4中的曲线1 Sym7、曲线2 Db7、曲线3 Coif4分别表示在各自的小波族[11]中取得最大的SNR和最小的RMSE。可以看出,选用Coifn小波基,消失矩阶数为5时,SNR改善最好,为5.75 dB,优于其他两个小波基;但RMSE也随着消失矩的增加而增大,为1.109 dB。综合分析可得出,Sym7小波基能够得到较大的SNR和最小的RMSE,消失矩阶数为5时,SNR改善较好,为5.35 dB,接近Coifn小波基;RMSE改善最好,为0.094 dB,优于其他两个小波基,即Sym7小波基得到了最好的去噪效果。

因此,实验选取Sym7小波基对采集的超声波加噪信号进行分解降噪,重构后的波形如图5所示。

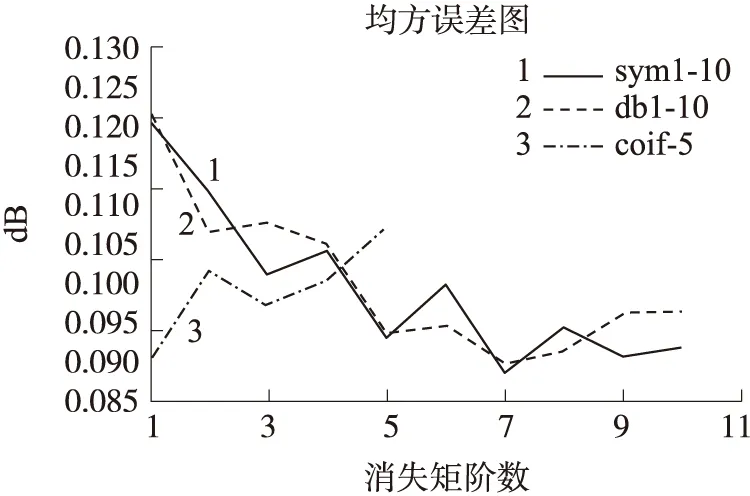
图4 不同小波基去噪后的的RMSE改善效果

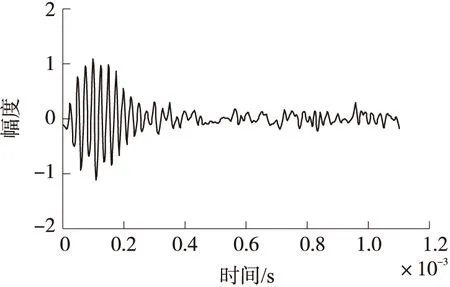
图5 选用Sym7小波基降噪后的重构效果

4 仿真结果及分析

利用Sym7小波基对加噪后的采集信号进行2层小波分解,依次按照硬阈值函数、软阈值函数[14]、半软阈值函数[12]进行处理。采用3种阈值函数去噪后的信号时域波形图对比如图6所示。

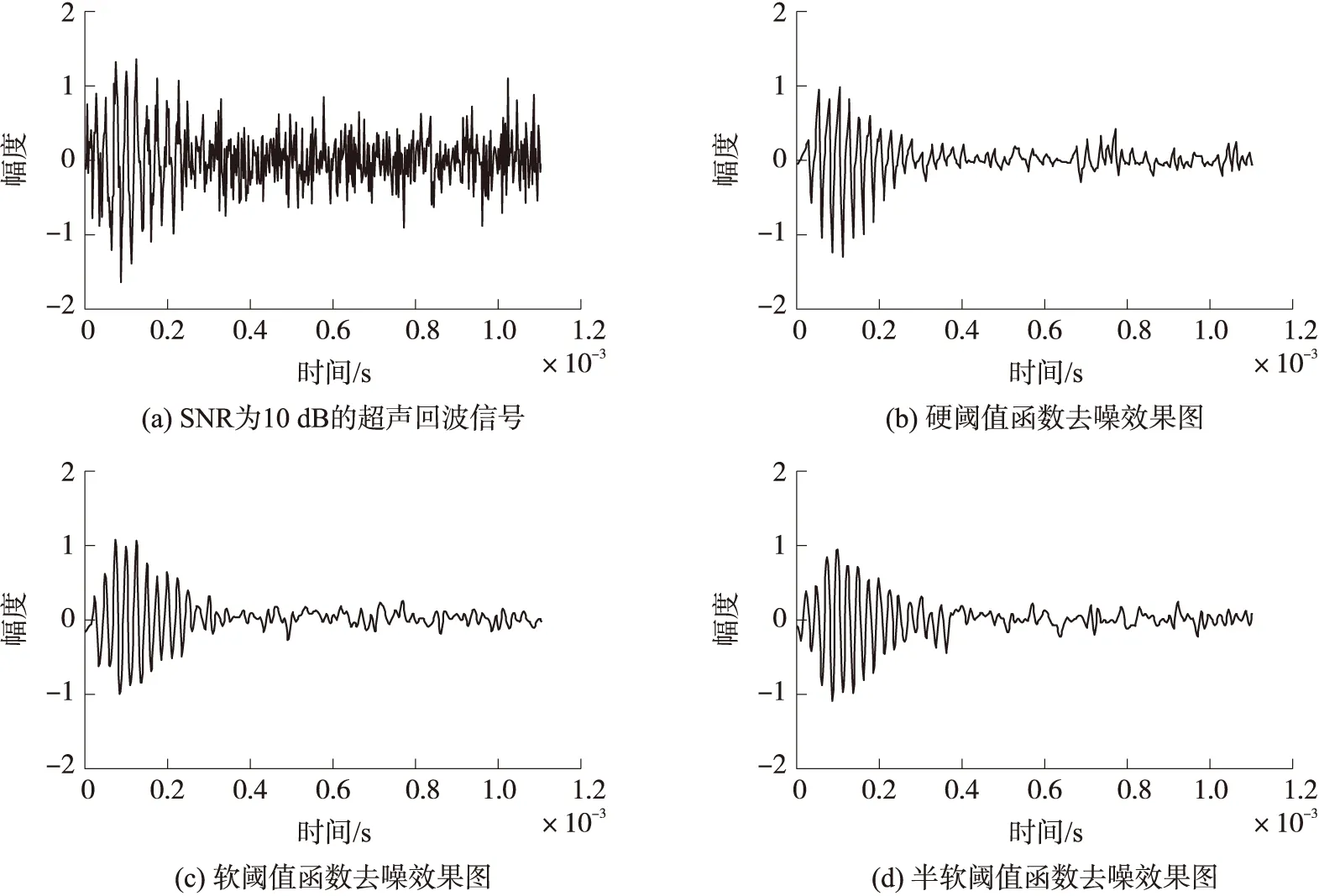
图6 3种阈值函数的去噪效果对比

从实验分析得出,在超声测距较远(2 m)、噪声污染严重(SNR为10 dB)的情况下,采用小波阈值法降噪有很明显的效果。在选取2层分解、消失矩阶数为5,选择Sym7小波基、半软阈值函数降噪时,信号SNR改善较大,为5.35 dB,RMSE最小,为0.094 dB,说明在有效去除信号噪声的同时,重构后的失真最小。

5 结束语

针对超声波测距的回波信号,提出了采用小波阈值去噪的降噪算法,在MATLAB仿真环境下,用硬阈值函数、软阈值函数、半软阈值函数,分别对超声波回波信号进行处理。实验结果证明,在选取2层分解、Sym7小波基、半软阈值函数核心参数后,信号的SNR和RMSE改善最佳,可以得到最好的去噪效果。

[1] 陈文会,刘芹,刘小民. 小波阈值去噪在FMCW雷达信号处理中的应用[J]. 计算机工程与应用,2015,51(8):195-199.

[2] 司祯祯. 傅里叶变换域小波变换在信号去噪中的应用[J]. 电子设计工程,2011,19(4):155-157.

[3] 黄贤源,隋立芬,范澎湃. 几种最优滤波方法的分析和比较[J]. 测绘工程,2007,24(3):35-39.

[4] 姜建国,王缇,孙磊. 基于小波变换和中值滤波的岩心图像去噪[J]. 科技传播,2009,7(9):77-78.

[5] Choi H,Baraniuk R G. Multiple Wavelet Basis Image Denoising Using Besov Ball Projections[J]. IEEE Signal Procession Letters,2004,11(9):717-720.

[6] 李冰祥,樊超,张维娜. 基于小波变换的稠油出砂信号去噪分析[J]. 电子测试,2011,22(11):1-4.

[7] 陶珂,朱建军. 小波去噪质量评价方法的对比研究[J]. 大地测量与地球动力学,2012,36(2):128-133.

[8] 张祥,杨飞鹏,黄宝莹. 基于包络拟合法的FPGA超声测距系统设计[J]. 电子技术应用,2012,41(7):14-16.

[9] 刘昕. 基于STM32单片机的高精度超声波测距系统的设计[J]. 电子制作,2013,46(16):10-10.

[10] 邓玉娟. 基于小波变换的语音阈值去噪算法研究[D]. 重庆:重庆大学,2009.

[11] 曹京京,胡辽林,赵瑞. 一种改进小波阈值函数的光纤光栅传感信号去噪方法[J]. 传感技术学报,2015,28(4):521-525.

[12] 郭晓霞,杨慧中. 小波去噪中软硬阈值的一种改良折衷法[J]. 智能系统学报,2008,3(3):222-225.

陈文会(1963-),男,通讯作者,陕西武功人,副教授、硕士生导师,主要研究领域为传感信号处理与自动检测。1986年从河北工业大学精密仪器专业大学本科毕业后在陕西省计量测试研究所从事精密测试技术研究和智能测试仪器的设计开发工作。1995年从西安理工大学测试计量技术及仪器专业硕士毕业。2006年从西安交通大学电子科学与技术专业博士毕业,whchen@139.com;

陈江宁(1991-),男,西安市人,硬件开发工程师,主要从事嵌入式系统设计工作。

The Parameter Selection Method of Wavelet Threshold Denoising in Ultrasonic Ranging Signal Process*

CHENWenhui1*,DINGXiaohong1,CHENJiangning2,LIUXiaomin2

(1.School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710129,China;2.Shanxi Maihang Traffic Control Ltd. Co.,Xi’an 710061,China)

Discuss the parameter selection and optimal by researching the de-noising problem of wavelet transform in ultrasonic echo signal. The detailed research about the parameters optimal including how to select the wavelet base,decomposition layers,threshold value and threshold function were fully discussed. Under the MATLAB environment,the hard threshold function,soft threshold function and semi-soft threshold function are utilized to deal with the ultrasonic echo signal of SNR 10 dB respectively. Experimental result shows that the semi-soft threshold function can reach SNR 5.35 dB and RMSE 0.094d B.

ultrasonic echo signal;wavelet de-noising;parameter selection

项目来源:2015年江苏省科委基金项目(0800/N2015KE0006)

2016-07-05 修改日期:2016-11-24

TV698.1+5

A

1004-1699(2017)03-0407-05

C:7230

10.3969/j.issn.1004-1699.2017.03.013