布谷鸟算法优化小波神经网络的短时交通流预测

黄晓慧 张翠芳

(西南交通大学信息科学与技术学院 四川 成都 611756)

布谷鸟算法优化小波神经网络的短时交通流预测

黄晓慧 张翠芳

(西南交通大学信息科学与技术学院 四川 成都 611756)

针对目前短时交通流的预测精度不够高这一问题，提出一种布谷鸟算法优化小波神经网络(CS-WNN)的短时交通流预测模型。首先采用小波变换对数据进行降噪，并进行归一化处理，然后使用复自相关法对具有混沌特性的短时交通流进行相空间重构，将交通流数据拆分为训练数据组和测试数据组，使用布谷鸟算法优化小波神经网络的各项参数，并根据训练数据组来训练优化后的小波神经网络模型。最后使用测试数据组的数据对CS-WNN模型进行有效性验证。仿真结果表明，相比几种主流的优化预测模型， CS-WNN短时交通流预测模型具有更高的预测精度。

短时交通流 复自相关 布谷鸟算法 小波神经网络

0 引 言

准确、实时的短时交通流预测是智能交通系统的基础和关键。短时交通流预测一般是指间隔时间不超过15分钟的车流量预测。用道路实时和历史检测数据，通过各种模型和方法预测下一时段的交通量，既可作为智能交通系统信号控制的设计依据，也可为出行者的路径选择提供参考[1]。

近几十年来，各国研究学者提出了众多的短时交通流预测方法。总的来看，有以下几类：基于线性理论，如文献[2]中提到的统计的方法；基于非线性理论，如小波分析、混沌理论[3]等；智能理论，如神经网络[4]、支持向量机；其他模型，如动态交通分配模型[5]。其中，神经网络由于自适应、自学习能力强而被广泛应用，典型的代表就是BP神经网络。

小波神经网络(WNN)是用非线性小波基取代通常的神经元非线性激励函数的一类新型前馈网络。对于非平稳的输入，小波神经网络有着比BP神经网络更好的时频局部特性和变焦能力[6]，所以本文选取小波神经网络作为预测模型。然而，小波神经网络仍然具有容易陷入局部最小值的缺点。为此，本文采用布谷鸟算法(CS)优化小波神经网络的各项初始化参数。由于实际的交通流数据具有一定的噪声，因此，本文采用小波变换进行数据降噪[7]，这样既提高了模型的预测精度，又保证预测模型可靠性。对于交通流序列，在模型训练开始前，还应考虑序列的混沌性，将数据映射到多维，以更好地挖掘数据中的隐藏信息[8]。

基于以上思想，本文提出了布谷鸟算法优化小波神经网络(CS-WNN)的短时交通流预测模型，仿真实验表明，相比其他模型，CS-WNN模型具有更好的预测精度。

1 短时交通流数据预处理

由于实际数据受影响因素较多，在模型训练之前，对数据进行预处理，有助于提高模型的预测精度。

1.1 小波降噪

数据有噪声是指数据中有错误或偏离期望的值。为了保证预测模型训练的可靠性，本文采用小波变换对数据进行降噪。小波变换是以非线性函数为基，通过伸缩和平移，将数据变换为低频和高频部分，低频显示其轮廓，高频显示其细节[9]。

可用信号和噪声信号的区别通常在于平滑程度和频率高低。其中，可用信号表现平稳，且为低频信号。本文的小波降噪的大致过程如下：(1) 分解一维信号。以某个母小波为基准，定义分解的层次N，对一维信号进行N层小波分解。本文使用小波工具箱中的sym4小波执行3层分解。(2) 阈值量化高频系数。使用设定的阈值进行软阈值量化处理。(3) 恢复一维信号。根据小波分解的第3层的低频系数和经过量化处理后的3层的高频系数，进行一维信号的小波重构[10]。本文的数据降噪效果如图1所示，可见，降噪后的数据走势更加平滑。

图1 原始数据与小波降噪后的数据对比图

1.2 归一化处理

由于数值波动范围较大，为了仿真执行的效率更高，本文对实测的交通流数据进行归一化处理，待数据预测完毕再进行反归一化处理。使用的归一化函数如式(1)所示：

(1)

其中，ymax默认为1，ymin默认为-1，x为当前要处理的原始数据项，xmax为所有要处理的原始数据项中的最大值，xmin为所有要处理的原始数据项中的最小值。

1.3 相空间重构

相空间重构由Packard等人[11]于1980年提出，它是混沌时间序列预测的基础。交通流正是具有混沌特性的一组一维时间序列，因此有必要对它进行相空间重构，将一维数据映射到多维。根据Packard提出的延迟坐标法对数据进行相空间重构，对交通流序列x1,x2,…,xn中的各项xi重构后为：

Xi=(xi,xi+τ,…,xi+(m-1)τ)

(2)

其中，i=1,2,…,n-(m-1)τ，τ为延迟时间，m为嵌入维，n为交通流序列的长度。由式(2)可知，要完成相空间重构，关键是确定延迟时间τ和嵌入维m。本文采用复自相关法[12]计算τ和m，并将数据拆分为训练数据组和测试数据组。

2 CS优化WNN的短时交通流预测算法

2.1 布谷鸟搜索算法简介

布谷鸟搜索算法是一种新兴的群智能算法，由YANG等人于2009年提出。它利用布谷鸟巢寄生的特点，将寻窝产卵这一方式运用到寻优过程中[13]。

布谷鸟搜索算法最重要的两个原理是寄生繁殖和莱维飞行。概括来说，它有以下3个规则[14]：

(1) 一只布谷鸟一次产一个卵，并随机选择一个鸟巢存放；

(2) 在一组鸟巢中，含有最优秀的鸟蛋的巢自动保留到下一代；

(3) 鸟巢数量是固定的，并假设布谷鸟的蛋被寄生的鸟巢主人发现的概率为P，且P∈[0,1]，这时鸟巢主人会抛弃外来鸟蛋或者重新建立一个鸟巢。

可以认为一个布谷鸟蛋就是一个解，鸟巢或者布谷鸟更新的过程即代表新解产生的过程。在以上3种理想的状态下，布谷鸟的寻优位置和路径更新式公式如式(3)所示：

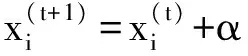
(3)

L(s,λ)～u=t-λ1<λ≤3

(4)

在搜索寻优的过程中，莱维飞行的短步长搜索有利于得到更优的局部最优点。而偶尔的大步长探索，又使算法不容易陷入局部极值点。

2.2 小波神经网络

本文选用的是紧密结合类的小波神经网络，又称小波与神经网络的有机式结合。用小波基函数代替前馈神经网络的激励函数，在小波基函数中的平移因子代替隐含层阈值，并使用了伸缩因子，改变了传统神经网络的模型结构。

本文所选用的3层小波神经网络的拓扑结构如图2所示。输入层有n个节点，n的值等于相空间重构所得到的嵌入维m，隐含层神经元个数为m，根据Kolmogorov定理，本文选取m=2n+1，输出层神经元1个。w和v分别表示输入层和隐含层之间的连接权值、隐含层和输出层之间的连接权值。Φ(x)为小波基函数。

图2 紧密结合类小波神经网络的拓扑结构图

由于Morlet小波基较强的抗干扰能力，广泛应用于预测领域，因此本文选用它来替代神经网络的传递函数。Morlet的数学公式为：

(5)

小波神经网络隐含层的输出计算公式为：

(6)

式中，p(j)为隐含层第j个输出，wij为输入层第i个神经元与第j个神经元之间的连接权值，h为式(5)中的Morlet小波基函数，aj为小波基的伸缩因子，bj为小波基的平移因子。

小波神经网络输出层的输出计算式为：

(7)

其中，vjk为隐含层与输出层之间的连接权值，p(j)为隐含层输出。

2.3CS-WNN短时交通流预测算法

算法的基本步骤如下所示：

Step1 导入交通流数据，并对数据进行去噪。使用复自相关法求得适合本次数据的时延τ和嵌入维m，完成相空间重构，并将数据拆分为训练数据组和测试数据组。

Step2 初始化小波神经网络，输入层节点m个，隐含层节点2m+1个，输出层节点1个。随机产生权值、小波基的平移因子和伸缩因子，并确定网络学习率和迭代次数等。本次实验选取的学习率为0.1，迭代次数为100，预测精度0.99。

Step3 设鸟巢个数Nnest为25，鸟蛋被鸟巢主人发现的概率Pa为0.25，迭代次数为N为200，随机生成Nnest个鸟巢位置W=(W1,W2,…,WNnest)T，每一个鸟巢Wi均有s个参数(s=输入层与隐含层权值个数+隐含层与输出层权值个数+平移因子个数+伸缩因子个数)。小波神经网络根据每个鸟巢初始的各项参数进行训练，计算每个鸟巢下的预测值，并根据预测误差找到这25个鸟巢中误差最小的鸟巢标记为鸟巢Wbest，并保留至下一代。

Step4 根据位置和路径更新式(3)对除Wbest以外的其他鸟巢进行更新，并通过小波神经网络计算预测误差，与Step3中的除Wbest以外的其他鸟巢的预测误差进行对比，以误差较小的鸟巢替代误差较大的鸟巢，从而得到当前代的较优鸟巢位置。Wnew=(Wnew1,Wnew2,…,WNnewnest)T。

Step7 训练数据输入小波神经网络，进行训练，若未达到迭代次数或预测精度，则不断学习，若达到迭代次数或预测精度，则小波神经网络停止学习，保存此时的各项参数值。

Step8 输入测试数据，进行实际预测。在预测的过程中，加入在线学习，根据前面预测的误差，动态地调整参数。最后，作图，并与真实值进行对比。

为了评价本文所提出算法的性能，选取3个评价参数：平均绝对百分比误差MAPE，平均绝对误差MAE，均等系数EC。

3 短时交通流仿真实验分析

实验选用的数据来源于美国明尼苏达州双子城交通管理中心(http://www.d.umn.edu/～tkwon/TMCdata/TMCarchive.html)，数据采自双子城高速公路，选取ID为10的探测器数据。原系统提供的数据为每隔30秒一组，并以专有格式进行了压缩，本文将其处理为间隔时间5分钟的车流量数据。数据的时间跨度为2015年11月16日至2015年11月20日，共1 440组数据。拆分数据的前960组数据作为模型训练数据组，后480组数据作为测试数据组。

实验硬件环境为双核英特尔酷睿处理器，2 GB DDR2内存。软件环境为MATLAB2011b。为了评价CS-WNN算法的优劣性，仿真实验中还引入了粒子群算法优化小波神经网络预测模型(PSO-WNN)、遗传算法优化小波神经网络预测模型(GA-WNN)、布谷鸟算法优化BP神经网络预测模型(CS-BP)的验证。这4种模型的各项评价指标(MAPE、 MAE、EC)见表1所示。

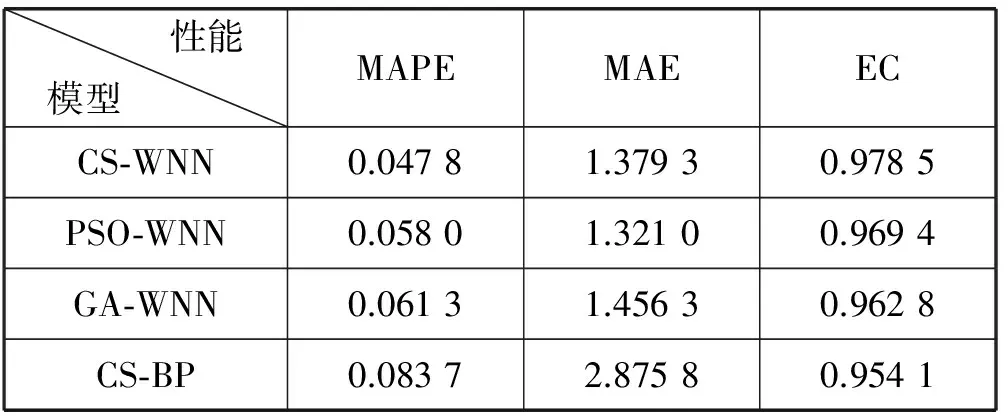
表1 不同模型短时交通流预测性能对比

由表1所示，对比CS-WNN和PSO-WNN 、GA-WNN，布谷鸟搜索算法比传统群智能算法平均绝对百分比误差、拟合度更高，布谷鸟算法优化后的小波神经网络对短时交通流预测有着更高的精度。对比CS-WNN和CS-BP，可知小波神经网络比BP神经网络的预测精度有明显的提升。考虑到间隔时间为5分钟的预测，三种算法的运行时间都较短，均在1分钟以内，因此都在可接受的时间范围，这种情况下预测的准确度越高越好。图3和图4为各模型短时交通流预测结果和实际交通流数据的仿真图。其中，图4 是将图3的仿真结果局部放大后的细节图。由图3和图4可看出，4种模型整体预测效果都很好，而CS-WNN模型预测效果尤佳，PSO-WNN模型预测效果次之，GA-WNN模型的预测效果略差于PSO-WNN，CS-BP最差。由表1和图3、图4可知，CS-WNN算法在整体性能上优于其他三种算法。

图3 各模型实际交通流预测结果图

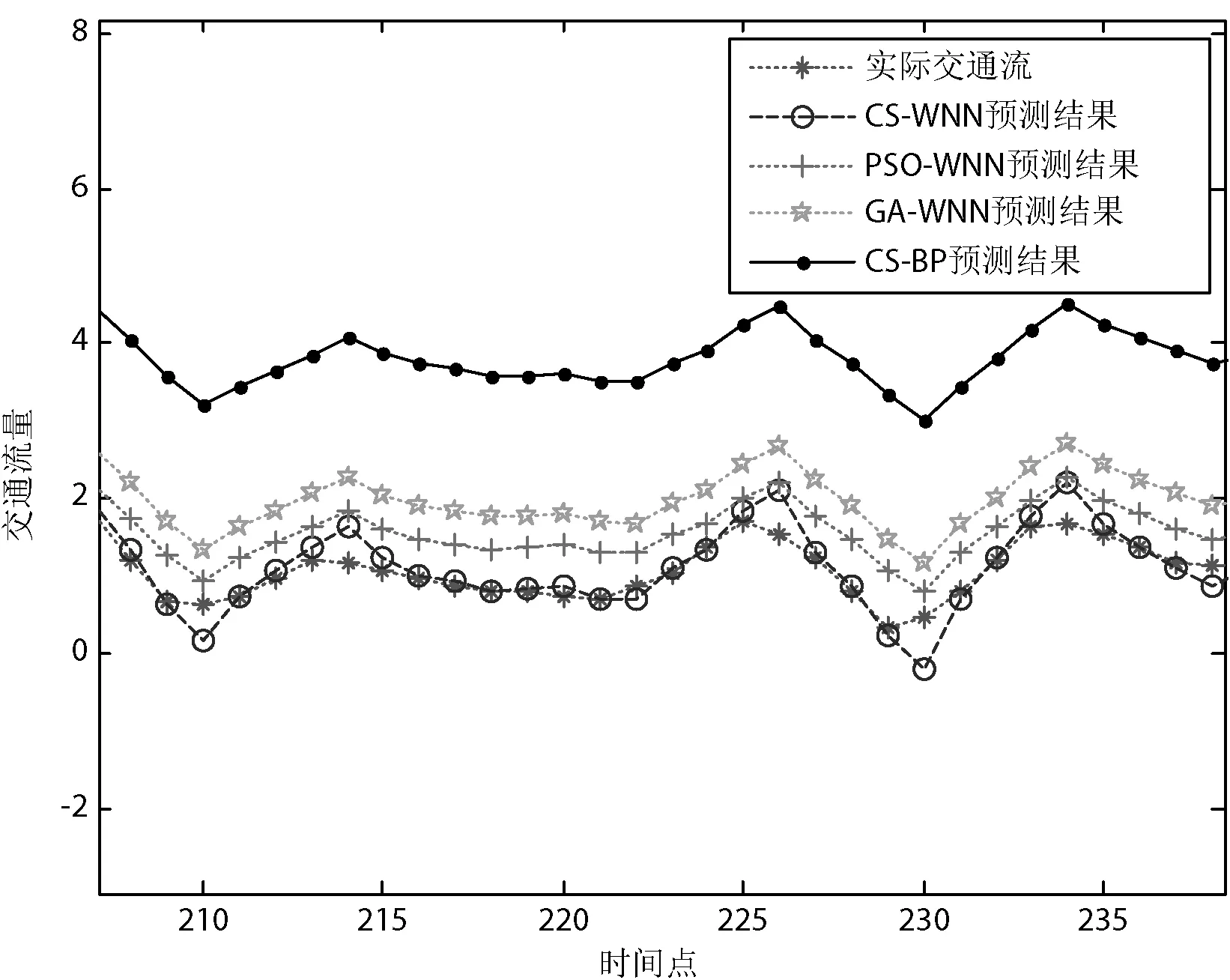
图4 各模型实际交通流预测结果局部图

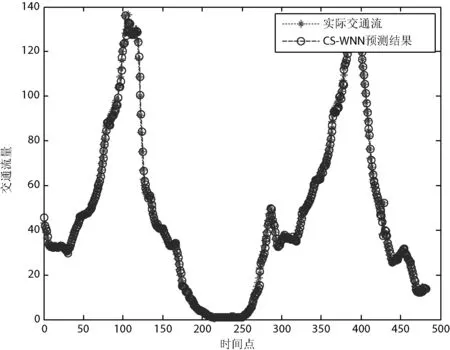
图5 实际交通流与CS-WNN预测结果图

图5表示单独运行实际交通流和CS-WNN预测结果的仿真图。相较图3和图4，图5能更清晰地看出，CS-WNN模型预测短时交通流的精确度较高，能较好地把握该实验路段车流量的走势，有着良好的应用前景。

4 结 语

首先从BP神经网络的结构上进行改进，使用小波基函数替代BP神经网络的激励函数，建立小波神经网络模型。其次，考虑到神经网络易陷入局部最小值的特点，将布谷鸟搜索算法与小波神经网络相结合，提出了布谷鸟算法优化小波神经网络(CS-WNN)的短时交通流预测模型。对比仿真实验，本文提出的CS-WNN算法具有更好的拟合能力和更高的预测精度。考虑到短时交通流易受临近路口和天气影响，在今后的研究中还将考虑多参数输入的预测模型研究。

[1] 袁健,范炳全.短时交通流预测研究进展[J].城市交通,2012,10(6):73-78.

[2] Fabio Moretti,Stefano Pizzuti,Stefano Panzieri,et al.Urban traffic flow forecasting through statistical and neural network bagging ensemble hybrid modeling [J].Neurocomputing,2015,167:3-7.

[3] 刘建华.相空间重构和SVR联合优化的短时交通流预测[J].计算机工程与应用,2014,50(4):13-17.

[4] 沈永增,闫纪如,王炜.基于混沌粒子群优化小波神经网络的短时交通流预测[J].计算机应用与软件,2014,31(6):84-86.

[5] 胡婷,于雷,赵娜乐.动态交通分配理论研究综述[J].交通标准化,2010,220(5):6-10.

[6] MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学,2010:208-217.

[7] 张宗平,刘贵忠,董恩清.基于二进制小波变换的信号去噪[J].电子与信息学报,2001,23(11):1083-1090.

[8] 李松,刘力军,解永乐.遗传算法优化BP神经网络的短时交通流混沌预测[J].控制与决策,2011,26(10):1581-1585.

[9] 周龙华,付青,余世杰.基于小波变换的谐波检测技术[J].电力系统及其自动化学报,2010,22(1):80-85.

[10] 袁飞.基于平移不变小波的语音信号去噪研究[J].自动化技术与应用,2011,30(8):40-42.

[11] Packard N H,Crutchfield J P,Farmer J D,et al.Shaw Geometry from a time series[J].Physical Review Letters,1980,45(9):712-716.

[12] 林嘉宇,王跃科,黄芝平,等.语音信号相空间重构中时间延迟的选择——复自相关法[J].信号处理,1999,15(3):220-225.

[13] Yang X S,Deb S.Engineering optimization by cuckoo search[J].International Journal of Mathematical Modeling and Numerical Optimization,2010,11(4):330-343.

[14] 李煜,马良.新型元启发式布谷鸟搜索算法[J].系统工程,2012,30(8):64-68.

PREDICTION FOR SHORT-TERM TRAFFIC FLOW BASED ON WAVELET NEURALNETWORK OPTIMISED BY CUCKOO SEARCH ALGORITHM

Huang Xiaohui Zhang Cuifang

(CollegeofInformationScienceandTechnology,SouthwestJiaotongUniversity,Chengdu611756,Sichuan,China)

Aiming at the improvement of the prediction accuracy of current short-term traffic flow, a prediction model for short-term traffic flow based on cuckoo search algorithm-optimised wavelet neural network (CS-WNN) was presented. Firstly, wavelet transformation and normalisation were used for data noise reduction, and the phase space reconstruction of short-term traffic flow with chaotic characteristics was done to form training data set and test data set by using complex self-correlation algorithm. Then, the wavelet neural network whose parameters were first optimised by cuckoo search algorithm was trained with training data set. At last, test data set was used for validating the effectiveness of CS-WNN model. Simulation results show that compared with several mainstream optimised prediction models, the proposed CS-WNN model for short-term traffic flow prediction has higher prediction accuracy.

Short-term traffic flow Complex self-correlation Cuckoo search algorithm Wavelet neural network

2016-01-22。黄晓慧，硕士生，主研领域：智能信息处理。张翠芳，教授。

TP183

A

10.3969/j.issn.1000-386x.2017.03.043