改进蚁群算法及其在云服务组合优化中的应用研究

李东星 陈 喆 钱双洋 焦 扬

(解放军信息工程大学 河南 郑州 450004)

改进蚁群算法及其在云服务组合优化中的应用研究

李东星 陈 喆 钱双洋 焦 扬

(解放军信息工程大学 河南 郑州 450004)

针对服务组合过程中的动态性、不稳定性以及多种QoS属性限制等问题，提出一个适应服务组合的改进蚁群算法WJ-I-ACO算法，包括基于聚类分析方法的改进局部优化算法和基于动态差分的改进全局优化算法。通过MATLAB仿真实验设计，验证了算法的有效性和可行性；基于此，分析了云服务组合的优化策略，给出了服务组合的路径寻优方法。

蚁群算法 云服务 优化 WJ-I-ACO

0 引 言

在云服务组合中，当服务组合模型生成后，为了给用户提供最为适合的服务，需要将功能相同的多个云服务或组合云服务进行动态选择提取，但在海量的云服务中，如何从中找出合适的服务来绑定到组合服务模式中，选择结果的好坏关系到服务组合的结果是否满足用户的需求。按照选择的依据可以将服务选择分为：基于功能需求的服务选择和基于QoS的服务选择。基于功能的服务选择是根据功能描述从服务注册中心选择出具有某种功能的服务。这种服务选择只能选择出在功能上满足用户需求的服务，但是在实际应用中，用户的需求不仅限于得到满足某种功能的服务，还需要考虑服务所需的费用、响应时间、是否可靠等，因此服务质量被引入到了服务选择中，即基于QoS的服务选择。基于QoS的服务选择从服务注册中心中选择功能上满足用户需求且服务质量在整体上满足QoS要求的服务。

蚁群算法不仅可以应用到网络服务软件测试和参数的优化问题上，还可以应用到TSP问题、测试集优化、背包问题、人工智能、神经网络、信号传输等一系列复杂问题中。但是，在实际的应用过程中，我们发现蚁群算法还是有很多不足之处，例如收敛速度不快、停滞很频繁等。随着人们的研究，很多学者针对以上蚁群算法的缺点做出了不同的优化和改进方法，比如，针对客服停滞问题的缺点，Stutzle等人[1]提出了MMAS(Max-Min Ant System)算法，主要是通过局部更新信息素的方法来克服这一缺陷。另外，针对收敛速度慢的问题，黄翰等人[2]结合马尔科夫的数学模型，给出估算收敛时间期望的理论算法。

张成文[3]提出了在优化以前对存在的问题进行编码，然后在全部的组合路径中选择满足用户服务的服务方案，显然，这个想法不符合实际需求，因为他没有考虑存在的动态性问题。Zeng等人[4]虽然考虑到了在服务选择中用户QoS属性值的动态变化，提出了用于服务指标感知的中间件，但是他们忽略了服务的不可用性以及选择流程中的一系列和动态相关的问题。倪晚成等人[5]用经典的最短路径算法进行服务选择，但是他们没有考虑到显示状态中复杂的服务状态。

介于上述原因，本文针对服务组合过程中的动态性、不稳定性以及多种QoS属性限制等问题，提出一个适应服务组合的改进蚁群算法WJ-I-ACO算法， WJ-I-ACO算法包括局部优化算法和全局优化算法两部分，局部优化算法利用聚类分析的方法将服务属性相同或相近的服务进行类聚，减少蚁群算法的搜寻节点，实现算法的局部优化。全局优化算法利用两条路径的动态差分平方统计量将相近的路径进行合并，实现蚁群算法的全局优化，两种优化使WJ-I-ACO算法能够适应服务组合优化过程中发生的服务无效，以及自适应服务中QoS变化等情况。

1 改进蚁群算法的设计与实现

1.1 经典蚁群算法描述

蚁群算法ACO又被称为蚂蚁算法，这是一种基于在图中寻找优化路径的机率型算法，同样它也是一种群集智能算法，由意大利学者Marco Dorigo于1992年最先提出。该算法的灵感来源于现实生活中蚂蚁的觅食过程。在蚂蚁寻找食物之前，没有食物所在位置的任何信息，所以刚开始蚂蚁都处于一种无规律的寻找状态。一旦有蚂蚁寻找到食物之后，这只蚂蚁会向环境中释放出一种具有挥发性的分泌物Pheromone(称为信息素，该物质会随着时间慢慢挥发消失，其浓度大小可以表示路径的远近)。根据这种分泌物，其他的蚂蚁也会找到食物，这样信息就会扩散出去，使越来越多的蚂蚁寻找到食物，同时在食物处产生更多的信息素，表现出一种信息素的正反馈现象。

蚂蚁在路径的选择过程中，可能有的蚂蚁并没有重复其他蚂蚁走过的路径，它们会另辟“蹊径”。即周围不存在信息素促使它选择某条路径，此时的蚂蚁就会沿着原来的运动方向随机挑选一条路径继续前进。为了防止出现在原地打转的情况，蚂蚁会记录并尽量避开刚走过的点。由于信息素会随着时间逐渐挥发，因此路径上信息素的多少可以表示该路径的长短，即路径越短，信息素就越多。蚂蚁在前进过程中，若感知到附近存在信息素，则会向信息素较大的方向前进，直至最后找到食物。因此，若某路径距离食物较短，这条路上的信息素就会相对较高，使蚂蚁聚集在一起收敛到最短路径上形成一种正反馈机制。具体过程如图1所示。

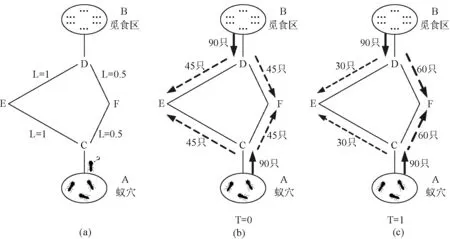
图1 服务自动组合实现框架

图1(a)中，A代表蚁穴，B代表觅食区，算法中的“蚂蚁”可以经由ACEDB和ACFDB两条路径往返于蚁穴和觅食区，有LACEDB=2LACFDB。先假设每个单位时间内都有90只蚂蚁从蚁穴出发经由路径ACEDB或ACFDB前往觅食区进行觅食，同时有90只蚂蚁从觅食区返回。单位时间内蚂蚁的移动距离相同，并释放等量的信息素，信息素会在(t,t+1)的时间内挥发消失。

在某一时刻，如图1(b)所示，C和D处各有90只蚂蚁，由于两条路径上初始信息素均为0，所有蚂蚁将随机选择路径，根据概率各有45只蚂蚁选择了路径CE、DE、DF和CF继续前进。

图1(c)表示经过一个单位时间后，即T=1时的情况，根据假设有90只新的蚂蚁在C处和D处出现，此时路径DE和CE在上一个单位时间内各走过了45只蚂蚁，释放了45个单位量的信息素，而路径DF和CF的长度是DE和CE的一半，共有90只蚂蚁走过，释放了90个单位的信息素。因此此时90只新的蚂蚁按照概率，选择路径DF和CF的蚂蚁会有60只，选择路径DE和CE的蚂蚁会有30只。随着时间不断增大，所有蚂蚁都将选择路径ACFDB。

1.2 组合云服务优化算法设计

智能优化算法的实现就是直接面向问题建立优化模型，这样我们可以根据其无关特性给予方便的求解。随着解空间的增加，智能优化算法优于经典的优化算法，因此，它比经典优化算法更加具有普遍适用性，目前存在以下三种优化策略：

① 局部策略：是将每一个子问题都求得满足用户需求的最优解，从而形成满足用户需求的最优组合服务，它适用于存在局部QoS约束的情况下。在时间性能等方面，局部策略相比较其他策略来说是拥有很好的性能，但是若在处理全局QoS需求方面仍存在着很大的缺陷。

② 全局策略：全局策略相比较局部策略来说，它是站在整体的服务质量上来说的，它根据服务对整体服务水平的贡献大小来选择服务，它着重考虑全局的质量，用以满足用户对服务组合的需求。传统的全局策略由于在任务的分解和服务发现与匹配的过程中实施面向单任务的服务组合，不能够保证用户需求的QoS指标全部被满足。在传统全局优化策略改进的基础上，另外加上了一个QoS协商约束机制，这样就可以和全局策略配合使用，共同寻找可行方案。

③ 混合策略：混合策略就是在上述两种策略的基础上寻求一种平衡。它的主要设计办法简单叙述如下，首先将全局的服务约束分成几个面向各个子问题的QoS约束；其次在各个子问题中局部约束的前提下，实现分布式的组合和优化过程。混合策略看似性能提升了不少，但是它仍然不能摆脱在传统全局策略下组合和优化所面临的缺点。

在云服务组合中，当服务组合模型生成后，为了给用户提供最为适合的服务，需要将功能相同的多个云服务或组合云服务进行动态选择提取，但在海量的云服务中，如何从中找出合适的服务来绑定到组合服务模式中，选择结果的好坏关系到用户使用的满意程度。

因此，如何建立一个合理的质量评价模型和使用何种高效算法可以在最短的时间内提供最优的服务就成为服务选择方法的有效性动态服务组合中急需解决的问题。这个动态的选择提取本质上就是组合云服务的优化，因此可将其归结为服务组合优化问题。

服务组合优化问题需要系统地考虑QoS属性约束，假设单一服务具有个QoS属性 ，对于每个QoS属性的服务相应的限定值 ，则各个QoS属性满足相应的约束，服务组合优化是在满足这些相应约束条件下，查找QoS总值最高的服务。与此同时我们也应该注意到各个QoS之间也存在着差异，比如数量级不同。如果QoS属性的值是成比例的服务质量的服务，较高的值表示较高的QoS，如带宽，一些服务质量属性的服务是成反比例的，比如服务响应时间。因此简单地加总不能反映真实服务的QoS，该问题的本质就是要解决单个服务选择问题，即局部优化问题。

在服务组合选择系统中，通过对多个单一服务进行选择来组合成一个复合服务，从而获得QoS更优的组合服务。单一服务的最优并不能保证组合服务的最优，因此通过局部组合优化后还需进行全局优化。

目前的服务组合方法都是伴随动态服务组合过程而动态生成的，其过程可以用一个有向图直观表述其结构，如图2所示。

图2 动态服务组合方法简单结构图

这里I表示输入接口，O表示输出接口，WSi(i=1,2,…)表示服务，WSi与WSj之间连线弧表示WSi的输出接口与WSi的输入接口匹配。

图2是较为简单的示例图，包含服务节点和服务边，图中非常容易找出最优的组合路径。但在复杂度较高的服务组合系统中，节点和边也相应较多，优化过程的复杂性也随之提升。因此，我们可以通过网状图形路径寻优的方法来解决服务组合优化问题。

定义1 服务组合有许多特性，其中包括顺序性、并发性等。顺序性指的是所有任务序列根据任务的执行顺序依次执行，这样的顺序就可以用单一路径图来表示；并发性指的是多个服务同时执行，不能用单一条路径表示，这种情况不适用于优化算法的使用，所以就需要把并行服务的先后顺序在逻辑上转换为顺序执行，即对服务进行串行处理。这种转换方式即利于优化算法的运行也不会影响实际的服务组合流程。

定义2 服务组合图的原点和终点分别表示服务输入，是动态生成的单向连接图。除了原点和终点不存在其他孤立点和悬点，所有节点的入度与出度均大于等于1，而且没有循环。至少有一个从原点到终点的路径。

在服务组合模拟图中每段弧表示一个抽象的服务(相同功能的同种类型的服务，作为候选服务的具体示例并未在图中给出)。基于单个服务组合的QoS优化，可以根据QoS的服务组合优化的总和来进行。服务组合模拟图如图3所示。

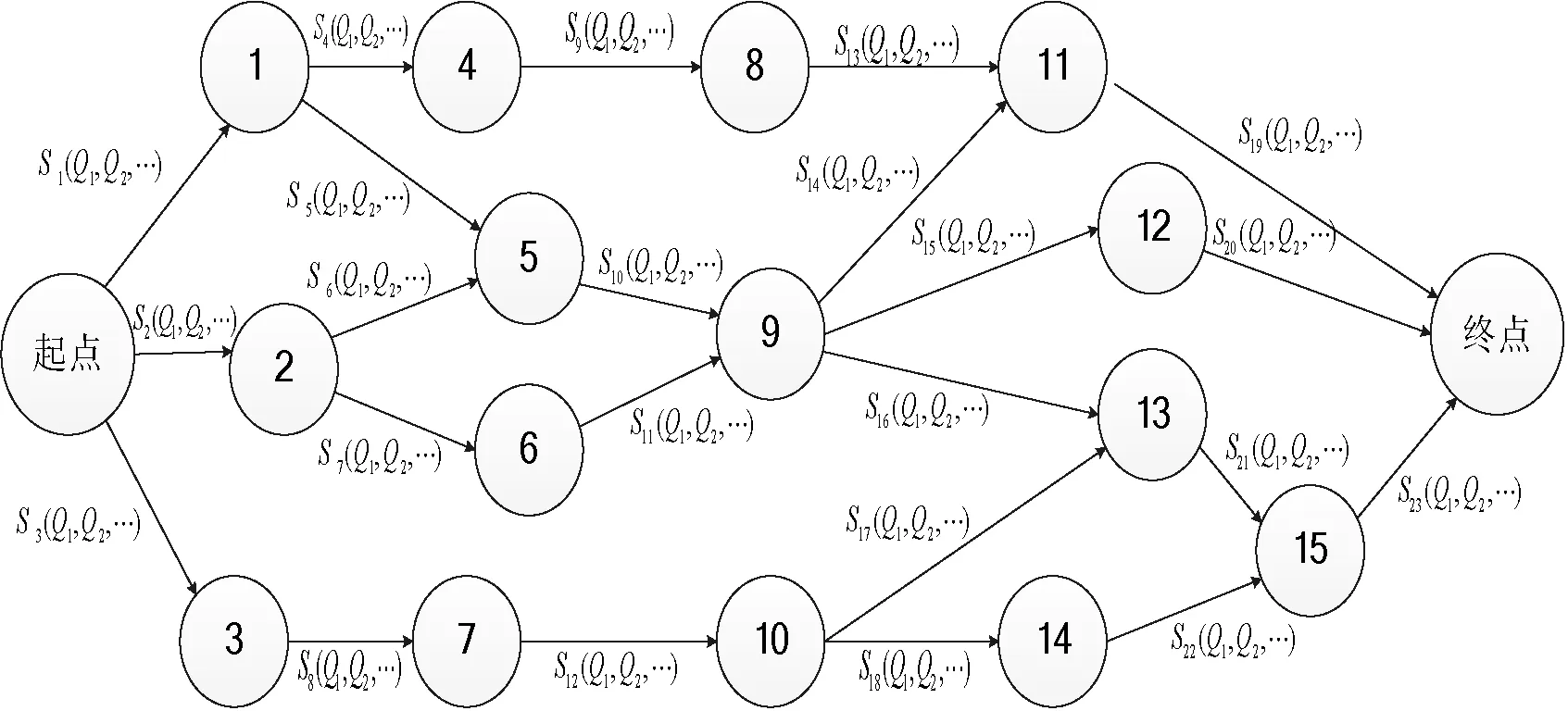
图3 服务组合模拟图

这里Si(i=1,2,…)表示不同的服务，Qi(i=1,2,…)表示不同的QoS属性。根据上图所示，服务组合优化问题就是在动态服务组合图中寻找最短路径的问题，将基于蚁群算法来解决该问题。蚁群算法其本身存在着收敛速度慢，易于停滞等缺陷，无法解决组合服务中多种QoS属性约束的问题；并且当循环次数逐渐增加后，信息素很容易聚集在少数几条路径上，使得易出现循环停滞、早熟等问题，从而得出的最终解决方案是一个局部最优方案。针对这些问题，下面将从局部和全局两个方面综合考虑给出一个改进的蚁群算法，为描述方便，在下文中表述为WJ-I-ACO算法。

1.3WJ-I-ACO算法状态转移概率

蚁群算法具有一定选择服务比较优良的概率，后来越来越多的蚂蚁通过正反馈机制选择更好的服务，最后发现在全域范围内最好的服务。因此，必须首先给出WJ-I-ACO算法状态转移概率的计算问题。不失一般性，设M为蚁群中蚂蚁的数目，N代表服务组合图的节点的数目，τij(t)为状态转移概率，我们可以分为两种情况来讨论状态转移概率τij(t)的计算方法。

1) 对单个QoS进行服务组合优化

当服务组合只考虑单一的QoS时，WJ-I-ACO算法就退变成为了基本蚁群算法，因而τij(t)的计算公式与基本蚁群算法相同。通过单一累加即可得到。

2) 对QoS总和进行服务组合优化

当考虑进行QoS总和来计算服务组合时，则需要将多种QoS属性值带入WJ-I-ACO算法求解τij(t)。

设s为路径(i,j)的一个服务，s共包含n个QoS属性Q1,Q2,…,Qn，这些属性对应的量化值转换函数为Q1(s),Q2(s),…,Qn(s)，则WJ-I-ACO算法中服务s的第r个QoS属性对应的信息素的计算公式为：

其中，w1,w2,…,wn为相应的权值。

综合以上两个计算公式得到τij(t)的计算式，下面进一步给出WJ-I-ACO算法的状态转移概率计算公式：

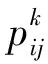
1.4WJ-I-ACO算法的设计与实现

针对蚁群算法收敛速度慢且易于陷入局部最优解等缺点，将通过分析组合云服务QoS优化的，给出WJ-I-ACO算法设计依据的寻优更新方法。

一方面，当利用蚂蚁算法进行组合云服务QoS寻优时，没有任何可以利用的先验信息可以使用，但当进行过多轮寻优之后，由贝叶斯判决可知，可以利用已查找到的路径信息，重新评估之前的路径，更新获得更优的路径。由此可以得到WJ-I-ACO算法寻优更新方法1。

方法1 经过多轮蚂蚁寻优后，比较每条路径中各节点的信息素浓度的大小，针对不同路径中服务相同的节点，重新评估之前所有路径，以信息素浓度大的节点重新构造新的路径，使该路径中浓度达到最大(表示QoS总和最大)，从而更新出新的最优路径。

另一方面，当利用蚂蚁算法进行组合云服务QoS寻优时，如果有一只蚂蚁优化过程中选择了全局最优路径，只要能够采取有效的方法证明该路径就是要找的最优路径，WJ-I-ACO算法就可以使算法找到全局最优解。可以通过建立最优列表方法来解决该问题，由此可以得到WJ-I-ACO算法寻优更新方法2。

方法2 设定最优路径列表L，把每一轮蚁群寻优后的浓度中最大的(对应的QoS)路径进行比较，按照最优顺序保存l个最优路径(浓度最大)到路径L中，浓度最大的排在第一位，以后以此类推。当算法达到循环的最大次数后，所排列的第一个元素与列表中每个路径的最高浓度进行比较，如果得到的结果相同，那么我们就可以根据该算法求得全局最优解，服务组合最优解即为浓度最高的路径；如果不同，则表示算法收敛于局部最优解。

方法2是一个简单而有效的解决方案，但是其中存在着一个问题，就是当蚂蚁在选择路径的时候没有选择最优的路径，这时我们依据该算法就得不到最优解。为避免此类情况，通过对算法进行动态跟踪，判断算法是否收敛于局部最优解，如果是，则忽略掉此次蚂蚁选路的概率，使得算法趋向于最优解的概率增加。

这里尽管给出了WJ-I-ACO算法设计依据的寻优更新方法，但也只是从宏观上给出了解决方案，对于算法在实际寻优过程中具体如何操作尚没有解决，下面从局部寻优优化和全局寻优两个方面分析给出WJ-I-ACO算法的具体方案。

1)WJ-I-ACO算法局部优化算法

上述分析表明一个抽象服务有多个候选服务实例，这也确定了两节点之间有多个候选服务，如图4所示。如果所有路径都进行优化，那么优化计算规模将是非常巨大的，组合优化问题随着问题规模的增加而成倍增加。

图4 多候选服务结构图

事实上，如果能把大规模的优化问题分解或减成小规模的优化问题，尽可能缩小问题的规模，那么将大大提高算法的寻优能力。

WJ-I-ACO算法局部优化算法包含两部分：预计算部分和随机选取寻优部分。预计算部分将服务属性相同或相近的服务进行聚类，将这些服务归作一个服务节点不再单独区分。此外，也可以在预计算中设定限定条件将不满足的服务从寻优列表中删除，达到减少搜索量的目的。

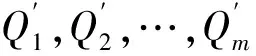
显然，当两个服务s与s′相同或相近的时候，C(s,s′)的值将趋向于零，以此来判断两个服务的相近程度。但这样的判定方法也存在如下问题：当服务s与s′的匹配指标趋向于零，而且服务s′与s″的匹配指标也趋向于零。但s′与s″的匹配指标确有可能并不趋向于零，这时候就难以将这三个服务归为一个分类。针对这种情况，采取将服务s与s′归为一类，将服务s″作为待定类，当所有属性近似的服务的匹配指标计算后，如果服务s″和某一类服务中的大多数服务的匹配指标都趋向于零，则将其归为其同类。

此外，考虑到动态服务组合和服务质量存在不确定因素，因此我们可以将状态转移概率的路径选取策略做如下调整：首先我们不通过计算概率值来选择服务，而是随机选择服务，然后利用状态转移概率计算作为过滤服务，把那些不能够满足用户需求的服务及QoS值低的服务去掉(对应于浓度低的弧)，通过这个办法我们可以缩小服务选择空间，提高运算效率。具体地，WJ-I-ACO局部优化算法由算法1给出。

设Ncmax为最大循环次数，M为蚂蚁个数，Lij为最优服务列表，下标i，j对应表示本次服务选择对应的服务组合图中的抽象服务Sij，初始化时间片t=0，循环控制变量Nc=0，蚂蚁循环变量k=0。

算法1WJ-I-ACO局部优化算法

Step1 匹配指标计算

根据服务组合中各服务的属性集合的不同，计算其匹配指标，其计算公式如下：

根据C(s,s′)的不同对服务进行分类，将属性集合看作路径节点。

Step2 服务随机选取

将蚂蚁所在节点对应服务的QoS属性Q1,Q2,…,Qn与其限定值q1,q2,…,qn进行比较，若达到要求则计算该服务的QoS总和，否则忽略该服务，并采用更新方法1对最优服务列表Lij中服务更新。

Step3循环迭代

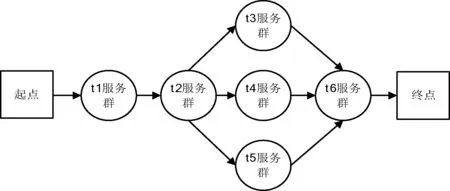
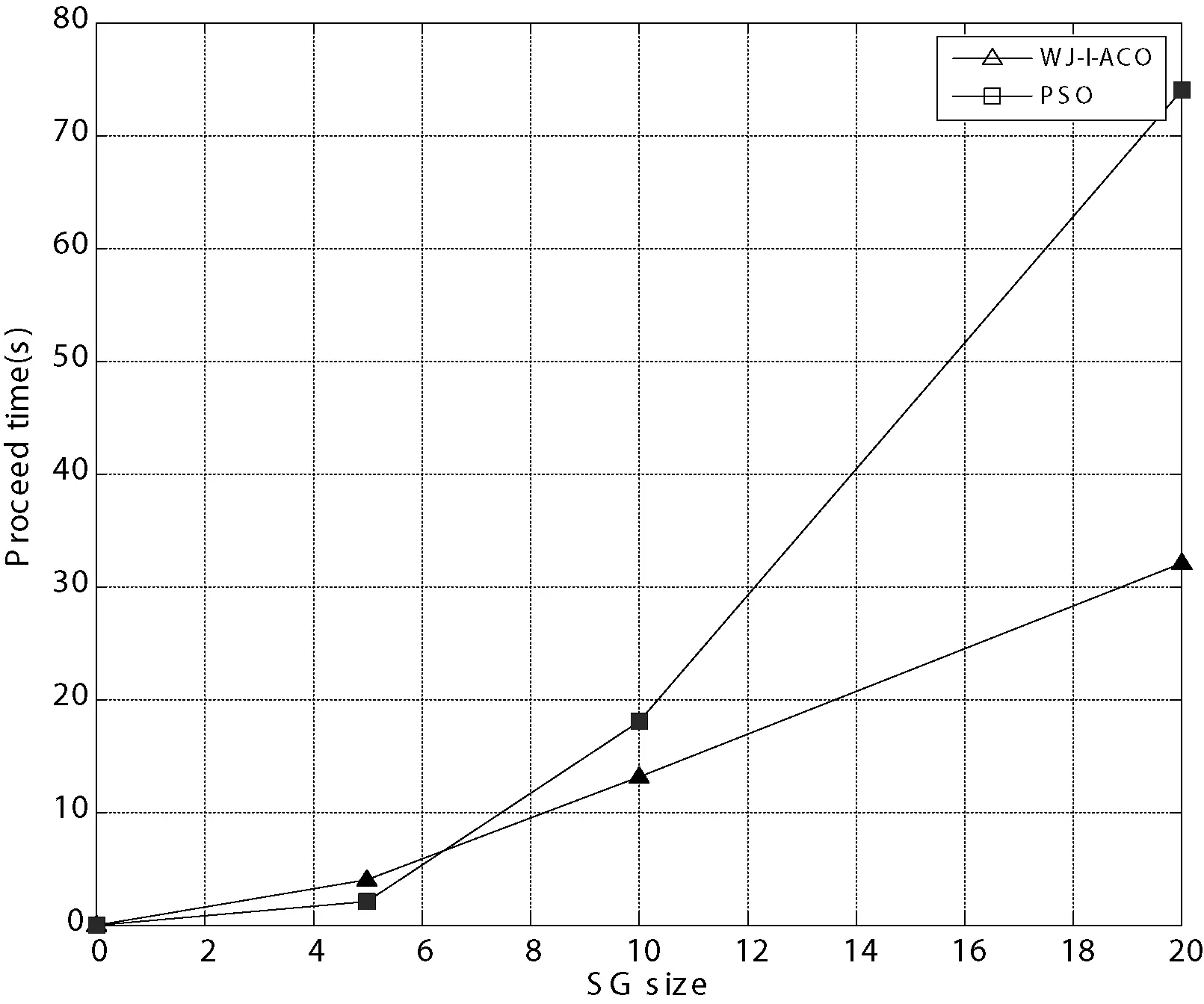
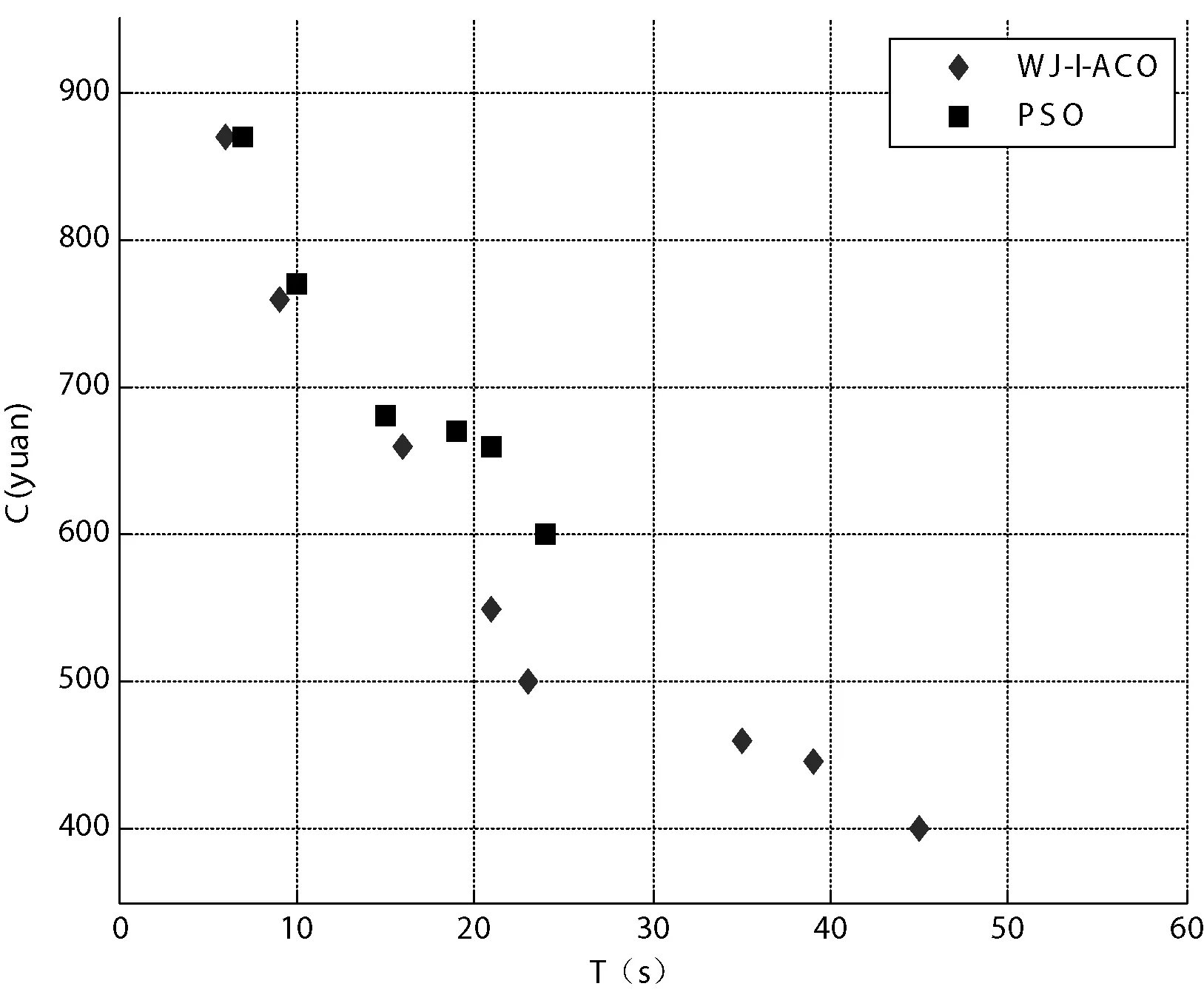
如果Nc

Step4 转移概率计算

如服务存在，则在服务列表Lij中选取最优服务计算其转移概率，选取其中转移概率最大的服务计算值，即是我们所选的最优服务。如服务列表Lij为空，则表示本轮服务选择失败。

Step5 服务删除算法

通过迭代计算，选取最优服务后，删除其他备选服务。

不考虑第一步预计算部分，该算法的复杂度是O(Ncmax×M)，其中Ncmax为最大循环次数，M为蚂蚁数量。该算法的最大复杂度为O(N×M)，其中N为候选服务个数。

2)WJ-I-ACO算法全局优化算法

通过对每个抽象服务进行局部优化后，再在全局内进行寻优的组合服务。全局优化算法首先通过一定的搜索后建立寻优路径列表，从历史经验条件出发，以历史经验最优路径为标准，通过动态求差的方法，对建立的路径列表进行筛选，缩小最优路径搜索空间，最后再搜索空间中浓度最高的路径进而得到最优路径。

针对全局搜索的情况，当所有的蚂蚁选择的路径都不是最优的，我们可以采取将历史经验最优路径设为最优路径，进行全局最有搜索。

设通过搜寻获得的按大小顺序保存的最优路径列表为L={lQ1,lQ2,…}，历史经验最优路径为lQ，把L={lQ1,lQ2,…}路径与路径为lQ进行如下动态差值运算，这里记为D(lQi,lQ)。

显然，当lQ与lQi越接近，D(lQi,lQ)的值将越小，以此来判断两个路径的接近程度。搜索完所有最优路径列表L={lQ1,lQ2,…}中的路径，只保留列表中与lQ接近的路径，以此完成对路径列表的优化。为了提高算法运行的效率，缩小服务组合的选择空间，我们过滤掉不满足要求的服务及QoS值低的服务(对应于浓度低的弧)，具体WJ-I-ACO全局优化算法由算法2给出。

设定最大循环次数Ncmax，蚂蚁个数M，初始化时间片t=0，循环控制变量Nc=0，蚂蚁循环变量k=0，最优组合服务列表L。将蚂蚁放置于服务组合图中的初始节点，令组合图中每条弧对应的各种QoS浓度值τij(t)为由WJ-I-ACO局部优化算法所选择服务对应的浓度值，如果没有相应的浓度值时，可令服务对应弧上的τij(t)=const，其中const为常数，历史经验最优路径为lQ。

算法2WJ-I-ACO全局优化算法

Step1 随着循环轮数的不断增加，即Nc=Nc+1，若出现Nc>Ncmax的情况，则跳出循环到Step7。

Step2 随着蚂蚁总数的不断增多，即k=k+1，若出现k>M的情况，则跳出循环到Step6。

Step3 按照转移概率计算公式，求出蚂蚁的所状态转移，即选择了当前两节点间对应的服务。如果选取服务的各QoSQ1,Q2,…,Qn的属性值过低或者服务不可用，则删除这个服务，同时在剩余节点中选择下一节点。

Step4 如果蚂蚁停止寻找下一节点且对应于组合图终点，则停止寻找服务，并将该节点路径保存到列表L中，跳转到Step5，否则跳转到Step3。

Step5 根据已选出的节点路径，得出其对应的服务组合，计算服务的各个子服务新增的加总。若蚂蚁总数k

Step6 根据L中最大的服务组合将其置于序列L的首位，如果列表已满，对表的路径计算：

只保留D(lQi,lQ)值较小的路径。

Step7 利用方法2，通过比较最优路径和最优组合列表L中的服务，得到算法的最优解即为最优的组合服务。

2 MATLAB仿真分析

2.1 仿真实验设计

本节我们主要是通过对一个城市规划的应用实例为背景来验证WJ-I-ACO算法的可行性和有效性。城市规划应用是通过将地理上分布的不同的空间数据资源和空间信息资源进行整合来自动地处理城市规划部门的问题。不同的数据和信息资源包括众多的服务类，如何从这些服务类中按具体需求选出最优服务组合，从而为城市规划部门的时间预算或经费预算提供有效的理论支持。

城市规划服务流程的具体的执行过程如图5所示。流程包含六个不同类型的服务群，每个服务群中含有不同数量、不同QoS属性的基础服务，服务群的建立和维护过程由指定的服务组合流程实现和管理框架来完成。其中，t1：请求解析服务；t2：地理编码服务；t3：行政区划分服务；t4：影像集成服务；t5：道路铺设数据服务；t6：数据集成服务。工作流程可叙述如下：接到规划部门的请求，对规划过程进行解析处理；将指点的规划区域通过空间定点描述转换成地理坐标；按照具体规划要求通过坐标划分行政管理区；对区域内进行摄像集成，形成图片描述展示直观信息；对主要的道路进行规划分析，通过最后所有数据的集成使得规划部门对周边地理环境信息做出直观、精确的判断，然后作出科学的决策。

图5 城市规划流程图

改进蚁群算法WJ-I-ACO用MATLAB实现，其中各个服务群中服务的QoS参数采用随机方法在一定范围内生成。

执行过程描述：

算法主要实现如下：

执行过程描述：

//为每个服务添加QoS属性综合值

If(E≠∅)

{for(eacheinE)

{for(eachserciceinservice(e))

{if(service-added==false)

//false表示服务的QoS值还没有添加;

{

character-value=F(service);

//添加QoS属性值;

service-added=true;

}

}}}

//在途中标注所有输入节点；

for(eachsi1insi)

{if(tag(si1)==false)

{标注节点si1;

tag(si1)=true;

}

elsecontinue;

}

//求出满足用户需求的所有最佳路径;

for(eachsi1→si2inkq)

{if(si1不可达si2)

//没有满足这种要求的服务;

buildingnewservice;

else{if(onlyonepathsatisfiedsi1→si2andmin(service(e)))

//有一条路径满足要求并求出路径上所有边标识服务集

//合中服务性能最佳的服务

selectservicesonthispath;

else

利用WJ-I-ACO算法求出所有min(service(e)中的最短路径

}

}

2.2 有效性的实验

在求解过程中，如果算法的每一次迭代时间过长将会造成具体问题求解速度慢的后果，即便算法能最后找到最优解也无法满足实际应用，此时算法就是无效的。为了验证改进蚁群算法WJ-I-ACO的有效性，我们设计了通过计算计算机CPU时间开销的方法来测量算法运行速度的实验。具体实验设计如下：首先将服务群规模设计了三种不同的类型，分别为5、10和20藉此来验证随着服务群规模的增加对算法运行时间的影响。其次，为了方便测量，限定算法的迭代次数，本实验中将最大迭代次数限定为100、200、300和400四种情况，为了避免计算机稳定性对算法带来的影响，对每种情况取10次平均值。由图6可以看出，WJ-I-ACO算法的有效性是非常明显的，因为服务群规模的倍数增加并没有造成算法消耗时间的成倍增加，在服务群规模为10的时候，算法循环400次仅需要12秒，这个运行时间也能满足大部分用户在服务组合时对时间要求的需要。

图6 WJ-I-ACO平均执行时间

2.3 可行性的实验

在验证了算法的有效性之后，还需对算法进行可行性实验，因为一个好的算法除了速度快之外，还应具有求解准确、优秀的特点，即能在一个限定的循环次数内，较大概率地找到最优解。为了验证采用WJ-I-ACO算法能够找到QoS全局最优服务链，我们做了以下实验。实验中采用的是穷举法，即列出所有可执行服务流程的最优解，验证在这些解集中存在最优结果的概率。为了实验验证方便，统计WJ-I-ACO算法循环200次的性能和开销的全局最优结果的百分率，如图7所示，服务群规模在5、10、20三种情况下，WJ-I-ACO算法在经过200次循环之后，性能和开销指标的最优值概率都超过了百分之九十。特别是在服务群较小的时候，算法在循环200次之后完全可以得到最优指标值，因此WJ-I-ACO算法在解决实际问题中是可行的。

图7 最优解的比例

2.4 优化策略分析

WJ-I-ACO算法先对每个抽象服务进行局部最优寻找后，然后再在全局内寻找最优的组合。首先通过一定的搜索后建立寻优路径列表，从历史经验条件出发，以历史经验最优路径为标准，通过动态求差的方法，对建立的路径列表进行筛选，缩小最优路径搜索空间，最后再搜索空间中浓度最高的路径进而得到最优路径。

为了验证WJ-I-ACO局部优化算法的时效性，将目前在实际应用中经典的局部优化算法粒子群算法(PSO)和WJ-I-ACO算法比较。图8 为在服务群规模分别为5、10、20的情况下，求得设定的一个特定解，算法PSO 与WJ-I-ACO花费时间比较，这里的时间为PSO 与WJ-I-ACO分别运行10次取平均。分析该图我们可以得到：在服务群规模较小的时候，粒子群优化算法寻找到某一局部最优解的时间比WJ-I-ACO算法短，但是随着服务群规模的增长，PSO算法花费的时间呈几何倍数增长。本实验中，在服务群规模等于5的时候，算法WJ-I-ACO开始比PSO求特定解的速度快，随着服务群规模的持续增加，WJ-I-ACO算法的优势愈加明显，寻优能力更加突出。

为了验证WJ-I-ACO全局优化算法求最全局优解的能力，设计在大规模服务群的情况下的仿真实验。图9所示的是在服务群规模为200，算法WJ-I-ACO和算法PSO的最优解的分布情况。分析该图可以得到，WJ-I-ACO算法的最优解的性能和分布比算法PSO更加优秀。WJ-I-ACO虽然提高了计算复杂性，但是通过该算法得到最优解的性能和质量好，PSO计算复杂性较低，但从图可以看出，在服务群规模增加到一定程度的时候，PSO算法将陷入局部最优，求得的解的性能和质量差，甚至在服务群规模特别大的时候将无法求得全局最优解。

图8 WJ-I-ACO和PSO的平均执行时间

图9 WJ-I-ACO和PSO的优化解集

3 结 语

针对服务组合过程中的动态性、不稳定性以及多种QoS属性限制等问题，提出一种优化的及适应服务组合的动态聚合信息素更新蚁群算法WJ-I-ACO以适应服务组合优化过程中发生的服务无效以及服务中QoS变化等情况。在此基础上，提出了一个以WJ-I-ACO算法为核心的云服务组合优化方法，并对云服务组合进行了动态性设计。下一步我们准备将语义网理论应用到蚁群算法之中，实现优化过程更高的智能化，并进一步寻找制约蚁群算法收敛速度的深层次原因以及算法对数据敏感性的规律。

[1] Singh S,Chana I.Resource provisioning and scheduling in clouds:QoS perspective[J].Journal of Supercomputing,2016:1-35.

[2] 黄翰,郝志峰,吴春国,等.蚁群算法的收敛速度分析[J].计算机学报,2007,30(8):1344-1353.

[3] 张成文,苏森,陈俊亮.基于遗传算法的QoS感知的Web服务选择[J].计算机学报,2006,29(7):1029-1037.

[4] Zeng Liangzhao,Boualen Benatallah.QoS-aware middle-ware for Web services composition[C].IEEE Transactions on Software Eengineering,2004,30(2):311-327.

[5] 倪晚成,刘连臣,吴澄,等.基于概念关联程度的网格服务组合方法[J].清华大学学报:自然科学版,2007,47(10):1581-1585.

[6] Aloes A,et al.Web Services Business process Execution Language,Version2.0 OASIS Standard (April 2007)[S].http://docs.oasis-open.org/wsbpel/2.0/OS/wsbpel- v2.0-OS.html.

[7] Comi A,Fotia L,Messina F,et al.A Reputation-Based Approach to Improve QoS in Cloud Service Composition[C]//Enabling Technologies:Infrastructure for Collaborative Enterprises (WETICE),2015 IEEE 24th International Conference on.IEEE,2015:108-113.

[8]LiuS,WeiY,TangK,etal.QoS-awarelong-termbasedservicecompositionincloudcomputing[C]//EvolutionaryComputation(CEC),2015IEEECongresson.IEEE,2015.

[9]KazemAAP,PedramH,AbolhassaniH.BNQM:ABayesianNetworkbasedQoSModelforGridservicecomposition[J].ExpertSystemswithApplications,2015,42(20):6828-6843.

[10]JatothC,GangadharanGR.QoS-AwareWebServiceCompositionUsingQuantumInspiredParticleSwarmOptimization[M]//IntelligentDecisionTechnologies.SpringerInternationalPublishing,2015:255-265.

[11]ZhengH,FengY,TanJ.AfuzzyQoS-awareresourceserviceselectionconsideringdesignpreferenceincloudmanufacturingsystem[J].InternationalJournalofAdvancedManufacturingTechnology,2016:1-9.

IMPROVED ANT COLONY ALGORITHM AND ITS APPLICATION IN CLOUDSERVICE COMPOSITION OPTIMIZATION

Li Dongxing Chen Zhe Qian Shuangyang Jiao Yang

(PLAInformationEngineeringUniversity,Zhengzhou450004,Henan,China)

Aiming at the dynamic, instability, multiple QoS attribute restrictions and other issues in service composition process, we propose an optimized and service combination fitted dynamic aggregation pheromone updating ant colony algorithm (WJ-I-ACO) , including improved local optimization algorithm based on clustering analysis and improved global optimization algorithm based on dynamic differential. The effectiveness and feasibility of the algorithm are verified through MATLAB simulations. Based on this, we analyze the optimization strategy of cloud service composition and give the path optimization method for service composition.

Ant colony algorithm Cloud service Optimization WJ-I-ACO

2016-03-15。李东星，硕士生，主研领域：云计算及其可靠性。陈喆，副教授。钱双洋，硕士生。焦扬，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2017.03.003