快速路行程速度突变段挖掘和基于相似匹配的短时预测算法
李心玥 杨卫东 张 徵 许海波
(复旦大学计算机科学技术学院 上海 201203)
快速路行程速度突变段挖掘和基于相似匹配的短时预测算法
李心玥 杨卫东 张 徵 许海波
(复旦大学计算机科学技术学院 上海 201203)
城市快速路交通流具有明显的畅通和拥塞时段交错的特征,其间行程速度产生较大变化。基于上海快速路线圈感应器采集的数据,首先提出一种在交通时间序列上线性时间挖掘行程速度突变段的滑动窗口方法,解决了识别拥塞起止时刻等需求。然后,构建突变段历史样本数据库和自定义索引,提出一套经过多重优化的基于相似度匹配的预测模型,达到对行程速度短时预测的目的,相比传统的回归方法更简单实用。最后,利用大量实际数据对两套模型的效果和性能进行了检验。结果表明,挖掘算法通过简单的参数调校可完成不同尺度的突变段查询,而预测算法能有效满足实时查询的性能要求,15 min的预测精度能达到90%左右。
时间序列 行程速度 突变段 滑动窗口 短时交通预测 相似度 索引构造
0 引 言
交通系统是国民经济发展的基本命脉,关系到商品货物的流通速度和人民出行的幸福指数。它的显著特点是大量随机或者周期性因素构成的不确定性:如天气(雨雪)等气象因素,交通事故或局部地区突发事件等人为因素,工作日早晚高峰和周末黄金出行时段等周期性因素。伴随着智能交通系统(ITS)研究的不断深入,短时交通流预测成为交通管理者和研究人员关注的主要问题之一,因为预测结果的好坏直接影响到ITS的决策和交通诱导控制的效果。短时预测是指预测时长跨度不超过15分钟的交通流预测,相对于已有较成熟研究成果的中长期预测,短时交通流预测的研究目前还处于发展阶段[1]。之前这方面的研究主要集中在预测交通量这一指标上,但交通量并不能很好地衡量交通状况:同一交通量水平在一个路段可能是严重拥塞,在另一个路段可能是畅行无阻[2]。因此,选择路段的行程速度作为研究指标,相比而言,它更直观反映了拥塞程度和路况。
本文基于上海市安装于快速路上的线圈采集数据展开工作。交通数据的采集主要有两种方式,一是静态交通探测方式,利用位置固定的定点检测器如线圈,雷达,光电检测器等;另一种是动态交通探测方式,基于位置不断变化的车辆或手机来获得实时行车速度和旅行时间等。无论哪种方式,采集数据的格式都可以表达为一连串密集的时间序列,横坐标为采集时间,纵坐标为该时间上侦测到的车辆行程速度平均值。
通过对快速路实际采集数据分析后发现,其行程速度多数时间有非常显著的低波动稳定性特征。图1为上海某快速路段某工作日的后台系统行程速度监测图,可将其视为一个时间序列。可以看出,当路面畅通或拥堵进行中时,时间序列会分别在高低位保持相对稳定,称这种时段为“稳定段”。相反,有时序列出现不同程度的大波动,例如逐渐进入早高峰的时段。相应地,称其为“突变段”。突变段有较大的研究价值,因为:(1) 突变段的识别是分析拥塞起止时刻和发生原因的基础[3];(2) 突变段对应了某些事故或突发事件逐步扩散过程,挖掘这些事件为相关部门制定准备方案带来帮助;(3) 突变段描绘了路段应对交通流变化的响应曲线,对交通规划部门有重要作用。
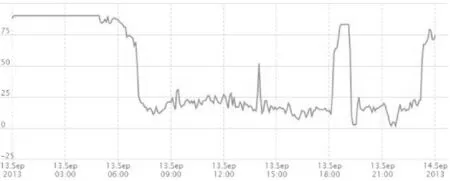
图1 快速路的时间-行程速度曲线
本文首先基于简单直观的累积弧度[4],形式化定义了时间序列上的突变段问题,并提出了挖掘突变段的方法。该方法利用滑动窗口存储已计算值的思想,能在线性时间搜索出序列中所有满足定义的突变段。然后,本文研究快速路上的短时预测问题。以往用数学建模求解的方法存在很多问题[5],越来越不能满足实际应用的需要,而较晚提出的基于非参数回归的模型[6]能较好应对交通流的复杂性,但需要构造状态向量等复杂步骤,且较难满足实时在线预测的要求。本文基于突变段,提出一种新的预测方法,核心是判断实时路况的当前状态,当路况触发突变阈值时,系统对历史突变段进行模式匹配,寻找出相似度最大的历史段,达到短时预测的目的。本质上采用了与非参数回归一样的假设,即历史数据库包含了由所有因素综合导致的交通状态变化趋势,可以认为所有因素的内在联系都蕴涵在历史数据库中。因此,只需足够的历史数据,就能较好地应对交通流这种不确定性强,非线性的动态系统,取得比传统建模方法更好的预测结果。
1 相关研究工作和联系
本文研究的问题之一是交通预测,已有的主要预测方法可分为: 1) 历史平均模型[7]等静态模型。它们静态地根据历史数据分析得出同一路段特定时间最大置信度的交通流。但静态预测不能解决非常规和突发的交通情况。2) 卡尔曼滤波模型[8]。由于其是线性预测模型,在预测交通流时准确率较低。 3) 神经网络算法[9]。但神经网络需要很大的训练样本,收敛速度慢,且有较多局限性。 4) 基于时间序列的自回归模型。代表是ARIMA自回归模型[10]。ARIMA通过三个模型参数p、d、q和一个方程去描述时间序列{yt},其中p是自回归周期,d是差分阶数,q是移动平均周期,通过该方程达到预测的目的。ARIMA模型试图用一个方程描述交通流这样复杂的非线性系统,且需要先根据序列识别一个试用模型,并不断做出调整参数,建模时间代价很大。5) 非参数回归方法[6,11]。其优点是不需要先验知识,拟合效果好,但也存在状态向量长度不易事先确定,状态向量较大时难以满足实时在线预测等问题。
本文使用时间序列作为研究内容的格式。时间序列在金融等领域都有广泛的研究。金融领域的时间序列强调形态特征的分析[12],如头肩底等。其他一些关于时间序列的研究方向有: 1) 时间序列的降维[13]。因为序列通常具有海量性,有时候需要将数据有效地压缩后才能处理。2) 寻找离群点和无效数据[14]。由于各种硬件故障、噪声干扰等原因,原始的交通采集序列需要先进行预处理[15],剔除异常数据,补齐丢失数据。另外,由于原始序列叠加了各种各样的干扰噪声,预处理阶段一般还需要采用噪声过滤技术减少数据震荡,经常使用的方法是均值平滑法或小波变换法。本文使用文献[16]提出的框架,利用小波变换法对原始采集序列先进行预处理,限于篇幅不再赘述,下文的时间序列均指预处理清洗后的数据。3) 时间序列的相似性度量。相似性度量的方法有很多,如基于欧式距离,基于模式距离等。本文利用了文献[17]提出的基于弧度距离的思想。
2 突变段的识别和挖掘
2.1 突变段问题定义
对于长度为n的交通时间序列s={y(t),t=0,1,…,n},首先定义基于相邻两点的分段弧度[17]:
定义1 对于交通时间序列s={y(t)},定义分段弧度rad(t)为(t,yt)和其相邻点(t+Δt,yt+Δt)构成的直线与时间轴的夹角弧度,即:
(1)
图2为分段弧度示意图,Δt=1。由定义1有,rad(t+1)=θt+1<0,rad(t)=θt>0,即当夹角在第1象限时为正值,第4象限时为负值。

图2 分段弧度示意图

使用k-累积弧度可以定量地分析在k尺度下序列的稳定程度。当cr(t)和rcr(t)较小时,说明t点处于一个稳定的弱波动水平中。当|cr(t)|相对左侧超过临界值时,表明序列在t点开始处于上升或下降的趋势特征中;相反,当|rcr(t)|相对右侧的超过临界值时,表明t点之后的趋势逐渐恢复稳定,t处于一段趋势的尾声。可以看出,当k=1时,累积弧度退化为cr(r)=rcr(t)=rad(t),尺度最小,只考虑了自身的波动。
定义3 对于交通时间序列S={y(t)},常数k和ε,k∈N+,ε>0,若存在子序列s={yi,yi+1,…,yj-1,yj},j>i+1满足:
1) 对于所有t∈(i,j),|cr(t)|≥ε;
2) 对于所有t∈(i,j),|rcr(t)|≥ε;
3) 且不存在子序列s′⊃s满足性质1和性质2。
则称子序列μ=(yi,…,yj)为交通时间序列{y(t)}的一个突变段,yi、yj分别为μ的起始点和终结点,j-i+1为突变段的长度。为了排除极小规模的波动的干扰,有必要设定常数L,使得定义3满足j-i+1≥L,保证突变段不小于一定长度。
2.2 时间序列上挖掘突变段的算法
下面给出基于定义3的在交通时间序列上挖掘突变段的算法1伪代码。
算法1采用了滑动窗口的思想。首先构造两个长度为L的滑动窗口winds[0]和winds[1],分别存储了当前已计算的L个点的cr和rcr值(第3行)。函数init初始化了头位置在head的滑动窗口。然后,算法1检查滑动窗口是否满足定义3的性质1和性质2(check函数)。若不满足,则窗口向后滑动最大的距离,跳过窗口内最后一个不满足的已计算点(第13~15行);若满足,根据定义3的性质3,窗口使用贪婪算法向后寻找更多满足条件的点直到失败(extend函数)。当找到符合条件的区间时,加入结果集合,并重新初始化滑动窗口寻找下一个区间(第7~12行)。当窗口向后滑动时,需要更新窗口值(第23~31行),如图3所示,阴影部分点的cr和rcr值得以保留并移动到滑动窗口队列头,算法从阴影后的点开始重新计算cr和rcr。step是窗口滑动的步数。
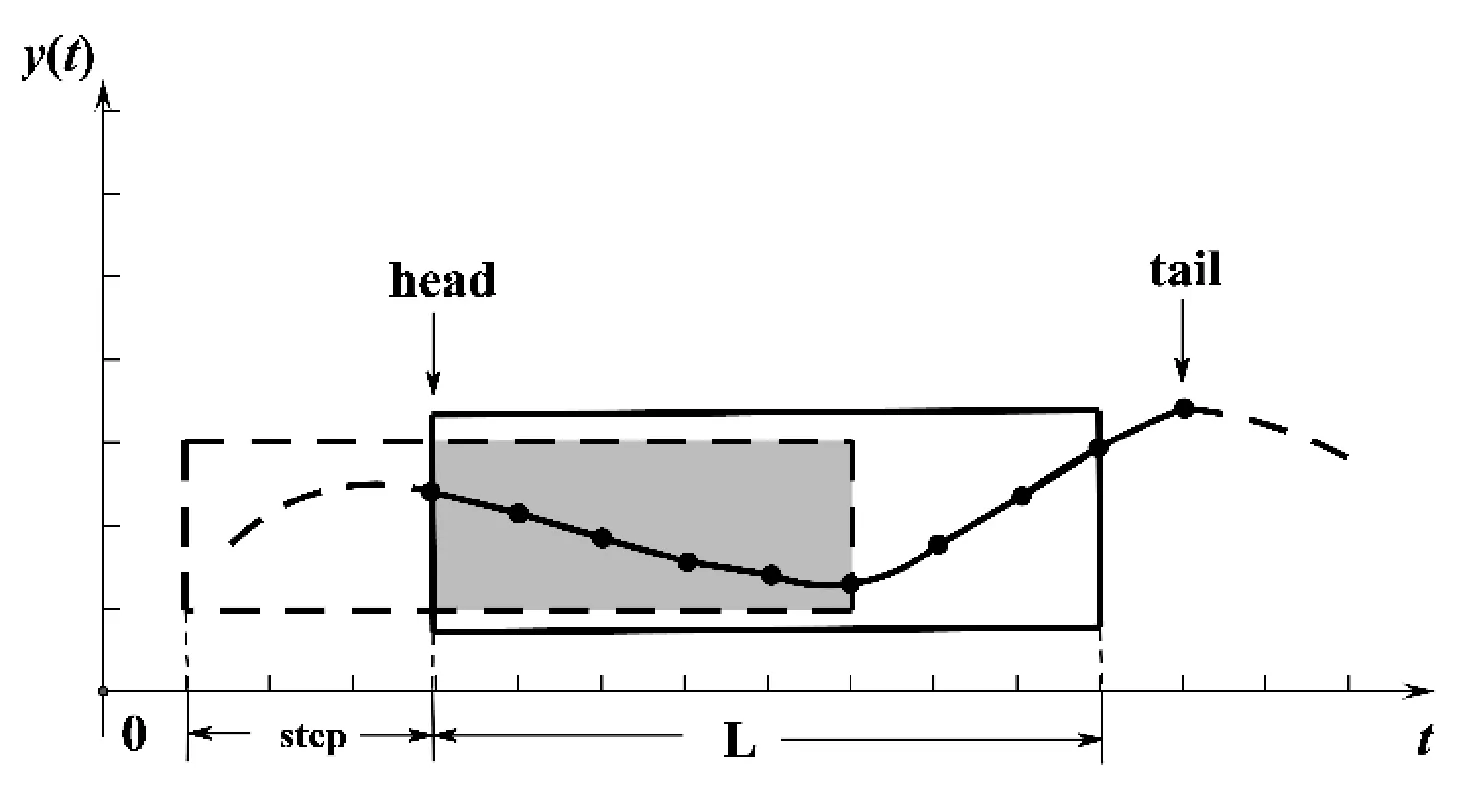
图3 滑动窗口示意图
算法1 挖掘突变段伪代码
输入:交通时间序列S=y{(t)},常数k,ε,L
输出:所有长度不小于L的突变段集合ω
1 ω=∅
2 head=k-1,tail=head+L,n=len(S)
3 winds=init(head)
4 while True:
5 step=check(winds)
6 if step==0:
7 end=extend(winds,tail-1)
8 ω=ω∪(head,end)
9 head=end
10 tail=head+L
11 if tail+k>n:break
12 winds=init(head)
13 elif tail+k-1+move≤n:
14 move(winds,head,step)
15 head+=step,tail+=step
16 else:break
17 def init(head):
18 winds=[]# a list contains 2 sublists
19 winds[1]=[cr(i) for in [head,head+L)]
20 winds[2]=[rcr(i) for in[head,head+L)]
21 return winds
22 def move(winds,head,step):
# 更新滑动窗口1
23 buffer=winds[0][step:]
24 cr_val=winds[0][-1]
25 cr_pos=head+L-1
26 dor iter in [0,step]
27 cr_pos+=1
28 cr_val=cr_val+rad(cr_pos)-rad(cr_pos-k)
29 buffer.append(cr_val)
30 winds[0]=buffer
# 更新滑动窗口2
31 ……
32 def extend(check_pos):
33 cr=winds[0][-1]
34 rcr=winds[1][-1]
35 while check_pow<=n-k:
36 if cr and rcr satisfy ε:
37 update cr and rcr
38 check_pos+=1
39 else break
40 return check_pos
41 def check(winds):
42 for pos in[L-2,0]:
43 if winds[0][pos]or winds[1][pos]not satisfy ε:
44 return pos
45 return 0
容易证明,init函数共执行|ω|+1次,时间复杂度O(L×k×|ω|),滑动窗口滑动并检验耗时O(n),整体复杂度O(n+L×K×|ω|)。因为k,L,|ω|≤n时,所以最后得到算法1的时间复杂度O(n),额外空间复杂度O(L)(不计输入序列)。
算法1的参数设置直观,通过简单调校就可以控制识别敏感度和突变段的趋势尺度。它只需对目标序列进行一次顺序扫描,并且不要求序列完全加载,因此也适用于流数据。这给实际应用中处理实时采集的数据带来了方便。
3 基于突变段的短时速度预测
3.1 预测模型和基本算法
基于上节的工作,建立如图4所示的快速路行程速度预测模型。其预测思想类似非参数回归模型[11],且基于城市快速路交通流的3个事实:1) 在车流量不超过设计承载值的畅通环境下,通过的单位时间车流速度稳定;2) 出行高峰时间,突降雨雪,上下游发生交通事故等各种情况下,都会影响行程速度,诱发突变段,产生趋势,但趋势行为会随着时间而改变,很难将时间-速度关系纳入一个统一的数学模型中;3) 相同的路段环境下,发生的事件在足够的历史数据下可重复,该路段应对相同事件的速度响应曲线是类似的。
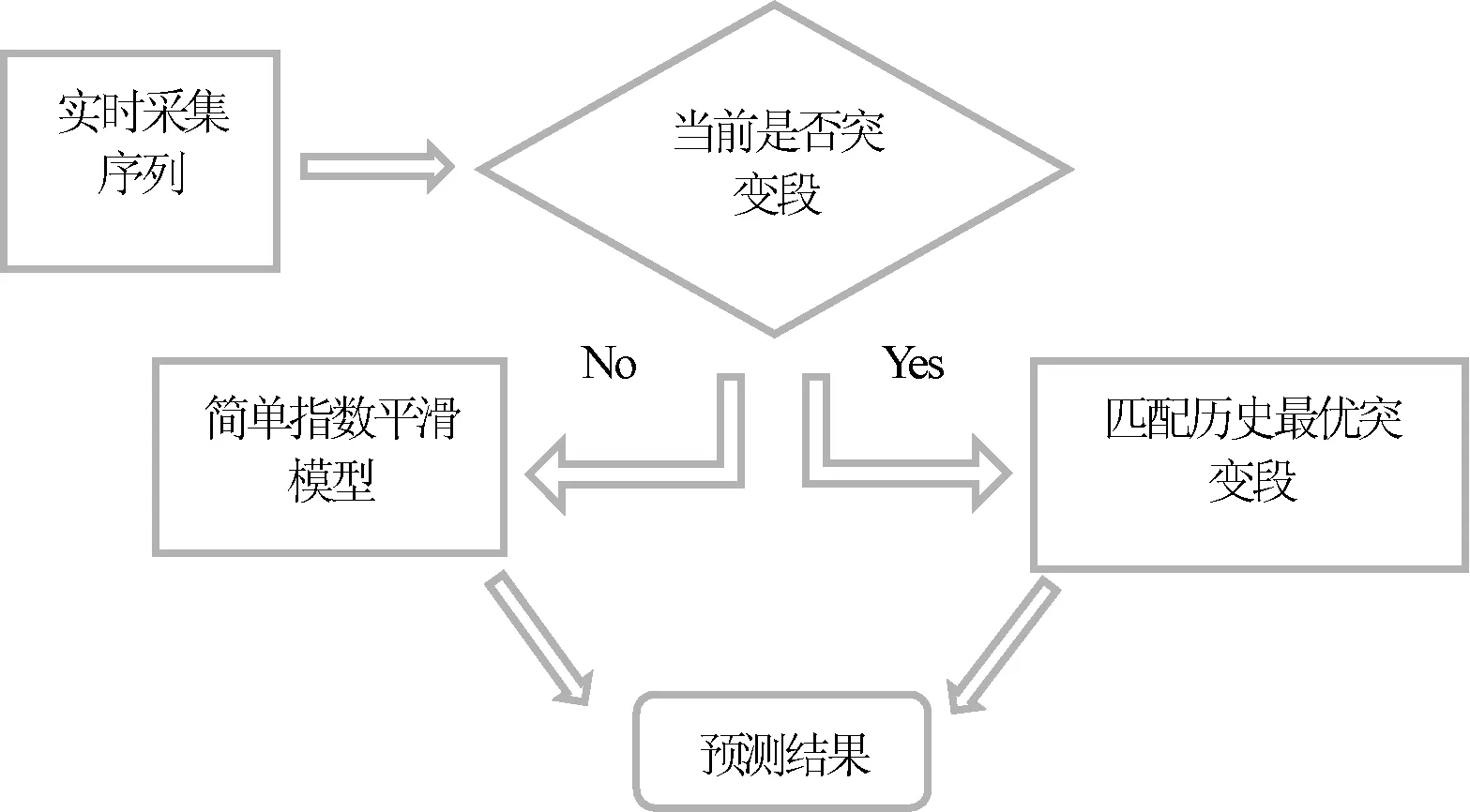
图4 预测模型框架
预测模型接受一个实时输入经过预处理的采集序列。令当前时刻为t,预测模型计算并输出Δt时间后的预测速度。
首先,通过算法1实时判断(t,yt)是否处于一个突变段中:
A) 如果否,使用简单的一次指数平滑法进行预测,其迭代方程为:
…+(1-α)kyt-k
一次指数平滑法适合于具有水平发展趋势的时间序列分析,能较方便地对短期进行预测。α为权重系数。
B) 否则,记当前突变段为Q={yi,…,yt},称为模式段。在该路段的n个历史突变段{sp},p=1,…,n中,查找与模式段最相似的匹配段{ye-(t-i),…,ye},满足:
1)yt≅ye;
2) {ye-(t-1),…,ye}⊆sq,q∈[1,n];
3)e=argmin(sim({yi,…,yt},{ye-(t-1),…,ye}))。

通过A-B两个步骤,预测模型反馈预测结果。因为输入数据实时变化,因此预测模型也可以实时更新预测结果。容易看出,该模型对较小的Δt有较好的预测值。一般要求Δt不超过15分钟。
算法2给出为模式段搜索匹配的伪代码。
算法2 模式段匹配伪代码
输入:模式段Q={yi,…,yt},历史突变段集合{sp}
输出:最佳匹配sq,匹配时刻e
1 best=∞,e=q=-1
2 for sjin {sq}:
3 for yhin sj:
4 if yh≅ytand yh-(t-i)∈sj:
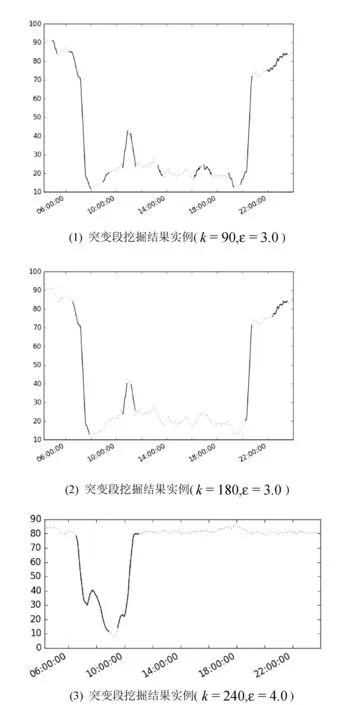
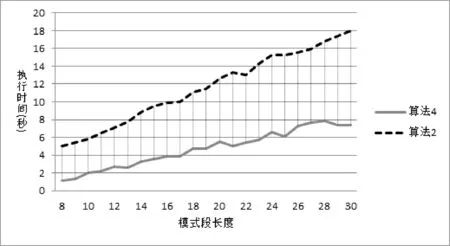
5 m=sim({yi,…,yt},{yh-(t-i),yh})
6 if m 7 best=m,e=h,q=j 8 return sq,e 3.2 相似性度量 时间序列的相似性比较有几种方法,例如基于欧几里德距离,重要点分段距离等,但一些方法并不能合理地判断两个时间序列的形态相似性,而一些方法则需要对y轴归一化处理,对幅度变化不敏感,这对预测模型而言是不可接受的。 (2) 当sim=0时,匹配段和模式段有完全相同的形态和值。定义类似基于模式距离的方法[18]。但传统的模式距离只考虑了三元模式,精度差,且需要进行对齐等额外处理。而该定义能够保留序列的形态特征,同时又对幅度敏感,计算方便,因此适用于本文的预测模型。 3.3 模式段匹配算法的优化 3.3.1 索引的构建 算法2需要对同一个路段的历史突变段数据库进行一次完整扫描,当数据较多时负担较大。实际上,根据算法2第4行,匹配段的值域必须包含模式段。因此,可以使用特殊的索引结构,排除不满足条件的历史突变段。基于此,设计索引如算法3-1所示。对一个路段,索引只需要构建一次。每次开始模式段匹配时,加载索引,通过算法3-2得到真正需要扫描的历史突变段集合,避免整体扫描。 算法3-1 索引生成 输入:{(yi1,yj1),(yi2,yj2),…,(yin,yjn)}表示的一个路段的所有n个历史非突变段 输出:索引Index 1 令序列L={yi1,yj1,yi2,yj2,…,yin,yjn} 3 for min[1,h): # 构造索引 算法3-2 索引查找 输入: 模式段查询{y1,…,yt} 输出: 根据索引找到的需进一步扫描的历史突变段集合H 1 H=φ 2 for min[1,h): 4 if H is φ: 算法3-1的原理是归纳并记录各个突变段的值域区间,当索引构建好后,对给定的模式段,使用算法3-2,能快速定位模式段值域范围内的突变段集合,并通过交集操作,保证输出集合里的每个突变段都能完全地覆盖模式段。 进一步,对于算法2第3-4行,还可以对各突变段构造倒排索引,使得给定yt可直接定位到yh,从而免去遍历突变段节点搜索yh≅yt的过程。下节的算法4第4行使用了这个思想。 3.3.2 相似度函数的下界优化 通过考察相似度函数的性质,能进一步对算法2进行优化。对sim函数,容易证明其存在一个下界: (3) (4) n是突变段的终点,cr(j,n)即为从j点出发到终点的累积弧度。对于每个突变段,可以预先离线计算从各点出发的到终点的累积弧度并存储;当模式段匹配动态进行时,通过式(4)迅速得出sim函数的下界。 利用式(3),对算法2进行改进。算法4给出了具体过程: 算法4 模式段匹配的优化 输入: 模式段Q={yi,…,yt},历史突变段集合{sp} 输出:最佳匹配sq,匹配时刻e 1 best=∞,e=q=-1 2 queue=PriorityQueue() 3 for sjin{sp}: 4 for each yh∈sjthat yh==yt: 5 Ibjh=lower_bound({yi,…,yt},{yh-(t-i),yh}) 6 queue.push(queue) 7 while queue not empty: 8 Ibjh=queue.pop() 9 if Ibjh≥best: 10 break 11 else: 12 m=sim({yi,…,yt},{yh-(t-i),yh}) 13 if m>best: 14 best=m,e=h,q=j 15 return sq,e 算法4的第4行先计算sim函数下界,这是当前匹配段和模式段至多能达到的最优相似度。然后,通过一个优先队列,优先计算目前拥有最优下界的匹配段,并不断更新相似度最优值。在队列不断出列的过程中,判断余下的未计算部分是否已经没有计算的必要(第9~10行)。通过此优化,能迅速过滤掉很多和模式段形态差距较大的匹配段,大大加快算法性能。 4.1 实验准备和数据源 本实验所用硬件环境为一台双核i3-3220,3.30 GHz,8 GB内存的台式电脑,操作系统为Ubuntu 15.10,所使用的语言为python3.4和R。实验数据来自上海交通部门提供的包含40个发布段,时间跨度从2013年9月到2013年11月的大约150万条真实数据,每条数据包含10列属性,包括时间,车速等。数据采集自上海快速路上设置的线圈传感器。在每个定义的发布段的车道上,布下多个线圈传感器,记录每辆车通过的时间,系统每20秒记录一次通过的平均车速。使用第1节论述的方法对数据先进行预处理清洗。 4.2 实验1 实验1测试突变段挖掘算法的实际效果。图5(1)-(3)为3组参数下的搜索示例图,取自上海内环高架新华路-吴中路匝道.该数据源每天的时间序列由4 320个点组成。图5中(1)、(2)为同一天数据。黑色实线代表挖掘出的突变段。 图5 测试突变段挖掘算法实效 使用3个指标作为挖掘结果的衡量标准,以便对结果的特征进行量化:(1) 结果数目;(2) 结果的平均长度;(3) 结果自身的波动大小(方差)。实验发现,模型的三个参数中,k和ε对搜索结果有较大影响,如图5(1)、(2)所示。较小的ε值会增大搜索的结果数目和平均长度。而较小的值会使搜索结果的趋势局限在更小的范围。对不同的发布段使用相同的参数,得到的3个指标也不十分一致。可能的原因是各发布段的路段格局,车流量,是否有限速行驶等条件不同。因此,实际应用中,需要对各个发布段的参数进行调校,使得搜索结果的特征符合使用者的需求。由于参数少且直观,调校过程并不复杂。在实验1中,我们通过枚举一系列参数值,人工对结果进行主观打分,从而为每个发布段选取一组主观最满意的参数,然后进行后续实验。 4.3 实验2 实验2使用预测模型,对普通工作日、双休日、普通公共假日及国庆期间等典型的日期先分类,然后进行短时速度预测。首先,把发布段数据样本按天分类,随机剔除3个普通工作日、1个强雨雪日、2个双周日和1个国庆日作为被预测样本,其余作为历史数据。然后,从每个被预测样本中截取多个代表时间段和突变段作为模型输入。从模型的输出结果中选取1分钟、5分钟和15分钟的预测结果。最后,将预测结果同被预测样本的实际速度曲线进行对比,统计各发布段预测的预测效果,如表1所示。 表1 不同发布段在不同预测时长下的误差统计 其中,误差指的是预测结果相比实际值的相对误差。平均误差是各发布段所有被测试段相对误差的平均值。可以看出,模型有较好的短时预测精度。在5min预测时长内可达94%左右的预测精度,15min预测时长内也有接近90%的预测精度。随着预测时间增长,模型的预测结果越不准确,这和直觉相符,因为预测时间越长,更多和历史数据条件不一致的随机因素会逐渐产生影响。因此,该模型适合短时预测。在实时预测中,可以不停地迭代更新模型的输入,修正预测结果。 4.4 实验3 实验3分析算法2和算法4的性能对比,以验证第3.3节提出的优化方案效果。在实验2的过程中,预先建立了相应的索引结构,分别使用算法2和算法4执行预测并统计完成时间。图6显示的是对不同被测模式段,其长度和预测算法执行时间的对应曲线。可以看出模式段的长度和执行时间大致成正比,因为计算sim函数时候的开销也相应增加。但在算法4中,因为计算sim函数下界的开销与模式段长度无关,所以带来的总体开销增长较慢。平均情况下,算法4能比算法2性能高32%左右,证明了优化的有效性。算法4可被用于实时交通流的预测。 图6 模式段匹配算法优化前后对比 快速路的突变段挖掘问题是根据实际交通需求产生的问题,基于累积弧度的定义方法简洁有效,具有挖掘不同尺度突变段的能力;基于突变段的行程速度预测模型为快速路的短时交通预测提供了新的思路和方法,它利用了历史数据库匹配的技术,实验证明了其能够取得比较准确的预测结果。未来的工作将着眼于在海量数据的实时在线环境下,如何通过大数据等技术,拓展本文的预测模型,进一步加强模型处理海量数据的性能和实用性。 [1] 高慧,赵建玉,贾磊.短时交通流预测方法综述[J].济南大学学报(自然科学版),2008,22(1):88-94. [2] 池红波.基于城市快速路实时观测数据的交通预测方法研究[D].北京工业大学,2004. [3]KrauseB,VonAltrockC,PozybillM.Intelligenthighwaybyfuzzylogic:congestiondetectionandtrafficcontrolonmulti-laneroadswithvariableroadsigns[C]//IEEEInternationalConferenceonFuzzySystems,NewOrleans,1996:FuzzySystems,1996:1832-1837. [4]DingY,YangX,KavsAJ,etal.Anovelpiecewiselinearsegmentationfortimeseries[C]//ComputerandAutomationEngineering(ICCAE),2010:The2ndInternationalConferenceon.IEEE,2010:52-55. [5]EleniIVlahogianni,JohnCGolias,MatthewGKarlaftis.Short-termtrafficforecasting:overviewofobjectivesandmethods[J].TransportReviews,2004,24(5):533-557. [6] 翁剑成,荣建,任福田,等.基于非参数回归的快速路行程速度短期预测算法[J].公路交通科技,2007,24(3):93-97. [7] Smith B L,Demetsky M J.Traffic flow forecasting:comparison of modeling approaches[J].Journal of Transportation Engineering,1997,123(4):261-266. [8] Okutani I,Stephanedes Y J.Dynamic prediction of traffic volume through kalman filtering theory[J].Transportation Research Part B Methodological,1984,18(1):1-11. [9] Dougherty M S,Cobbett M R.Short-term inter-urban traffic forecasts using neural networks[J].International Journal of Forecasting,1997,13(1):21-31. [10] Voort M V D,Dougherty M,Watson S.Combining kohonen maps with arima time series models to forecast traffic flow[J].Transportation Research Part C Emerging Technologies,1996,4(5):307-318. [11] 李振龙,张利国,钱海峰.基于非参数回归的短时交通流预测研究综述[J].交通运输工程与信息学报,2008(4):34-39. [12] Fu T C,Chung F L,Luk R,et al.Representing financial time series based on data point importance[J].Engineering Applications of Artificial Intelligence,2008,21(2):277-300. [13] Chakrabarti K,Keogh E,Mehrotra S,et al.Locally adaptive dimensionality reduction for indexing large time series databases[J].Acm Transactions on Database Systems,2002,27(2):188-228. [14] Mesnil Benoit,Petitgas Pierre.Detection of changes in time-series of indicators using CUSUM control charts[J].Aquatic Living Resources,2009,22(2):187-192. [15] Chao Chen,Jaimyoung,Kwon,et al.Detecting errors and inputting missing data for single-loop surveillance system[J].Transportation Research Record:Journal of the Transportation Research Board,2003,1855:160-167. [16] Liu li,He Xianping,Yuan Wenliang.A unifying framework for detecting outliers and change points from non-stationary time series data[J].Journal of Taiyuan Normal University,2011:676-681. [17] 丁永伟,杨小虎,陈根才,等.基于弧度距离的时间序列相似度量[J].电子与信息学报,2011,33(1):122-128. [18] 董晓莉,顾成奎,王正欧.基于形态的时间序列相似性度量研究[J].Journal of Electronics & Information Technology,2007(5):1228-1231. VELOCITY FLUCTUATION PERIOD MINING FOR EXPRESSWAY TRAFFIC FLOW ANDSHORT-TERM FORECASTING ALGORITHM BASED ON SIMILARITY MATCHING Li Xinyue Yang Weidong Zhang Zheng Xu Haibo (SchoolofComputerScience,FudanUniversity,Shanghai201203,China) Traffic flow on urban expressways has obvious characteristics that its travel velocity changes drastically between the smooth condition and the congestion. On the basis of data collected by coil sensors on Shanghai expressway, we propose a promising linear sliding window method to mine the travel velocity fluctuation periods in traffic time series, solving the requirements such as identifying the start and stop moment of congestion. Then, we construct the history sample database of fluctuation periods and the custom index, and propose an optimized forecasting model based on similarity matching to achieve the purpose of short-term forecasting of travel velocity. The model is more practical and intuitive than traditional regression model. Finally, we use huge amounts of real data to test the effectiveness and performance of these two models. Experimental results show that the mining algorithm can complete fluctuation period query at different scales through simple parameter tuning, while the forecasting model can effectively meet the performance requirement of real-time query and reach a high forecasting accuracy around 90% in 15 minutes. Time series Travel velocity Fluctuation period Sliding window Short-term traffic forecasting Similarity Index construction 2016-02-04。国家十二五专项(CHINARE2012-04-07,MJ-Y-2011-39);上海市重点基础研究项目(08JC402500);上海市高新技术创新专项(11CH-03);海洋公益项目(201405031-04);上海市科学技术委员会科研计划项目(14511107403)。李心玥,硕士,主研领域:交通数据挖掘分析,数据安全访问控制。杨卫东,教授。张徵,硕士。许海波,硕士。 TP392 A 10.3969/j.issn.1000-386x.2017.03.007


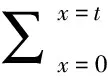
4 实验分析

5 结 语

