双离合自动变速器同步器监控策略开发∗

李鸿魁，鲁统利，张建武

(上海交通大学机械与动力工程学院，上海 200240)

双离合自动变速器同步器监控策略开发∗

李鸿魁，鲁统利，张建武

(上海交通大学机械与动力工程学院，上海 200240)

由于双离合自动变速器同步过程的复杂性，开环控制策略无法获得良好的控制效果。为改善同步器的控制性能，将同步过程分为6个阶段并进行了详细分析，建立了各阶段的数学模型。根据同步过程的动力学特点，针对同步器模型提出了一种监控策略，将接合套的位移和输入轴与输出轴转速代入各阶段的动力学方程来估计同步器所处的阶段，并设计不同的子控制器来控制各阶段的换挡同步力。实车对比实验结果表明，所提出的监控策略能有效降低同步延迟，减少了二次冲击的影响，有较高的工程应用价值。

双离合自动变速器；同步器；监控策略

前言

目前，双离合自动变速器(DCT)因其可无动力中断地从一个离合器转换到另一个离合器而被越来越多地应用到车辆上[1]。与传统手动变速器不同，双离合自动变速器依靠控制系统来驱动同步器操作以顺利完成换挡同步操作。

早期同步器的研究主要集中于同步器的结构设计和动力特性[2-4]。近些年，对于同步器的研究已经逐渐延伸到双离合自动变速器领域。双离合自动变速器同步器的设计和开发最早由Razzacki[5]和Walker等人[6-8]提出。由于同步器的复杂结构及不连续的动力特性，其控制问题十分复杂。文献[9]中提出了一种同步器分阶段控制方法，但是该方法无法处理由同步器部件磨损导致的控制性能下降的问题。因此，需要开发一种自适应控制策略来更好地实现换挡同步过程。

本文中将集中分析和开发一种新的监控方法，讨论监控内在的自适应特性。

1 双离合器自动变速器同步器数学模型

典型的锁环式同步器由接合套、同步锁环、花键毂、同步器定位销和待接合齿轮组成，其部件分解图如图1所示。

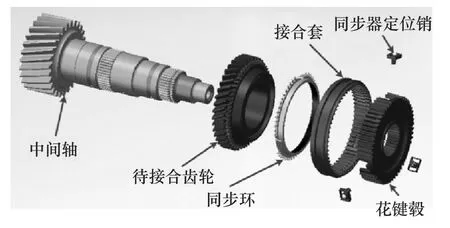
图1 锁环式同步器部件分解图

根据同步器不同部件之间的相互作用，同步过程可以被分为6个阶段。

阶段1：第一次自由行程。在这个阶段，同步器接合套带着同步环轴向移动以消除同步环与待接合齿轮齿圈的间隙。此阶段的动力学方程为

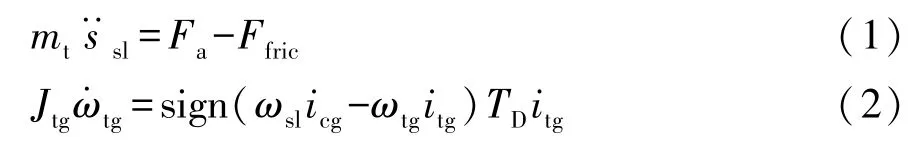
式中：mt为同步器接合套、同步环及定位销的质量之和；ssl为接合套位移；Fa为轴向力；Ffric为零部件之间的摩擦力；Jtg为目标齿轮处的等效转动惯量；ωtg为目标齿轮的角速度；ωsl为同步器接合套角速度；icg和itg分别为当前挡位和目标挡位的传动比；TD为输入轴处的阻力矩。

阶段2：克服定位销阻力。在这个阶段，同步器接合套将克服定位销阻力，继续轴向移动。此阶段的动力学方程为

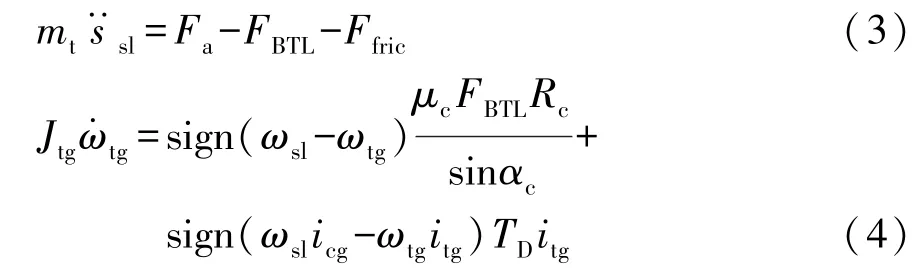
式中：FBTL为定位销阻力；μc为同步环与待接合齿轮齿圈之间的摩擦因数；Rc为摩擦面的平均半径；αc为摩擦面的半锥角。

阶段3：同步阶段。在这个阶段，同步环和待接合齿轮齿圈之间的摩擦力产生了一个摩擦力矩，它使两者的转速差逐渐缩小，直到转速相同。此阶段的动力学方程为

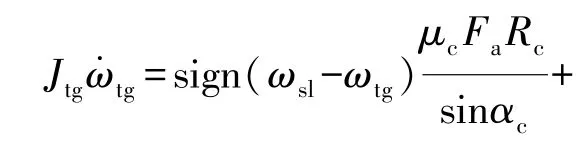
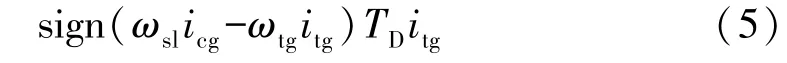
阶段4：拨环阶段。在这个阶段，同步器接合套将拨转同步环以实现与其啮合。此阶段的动力学方程为

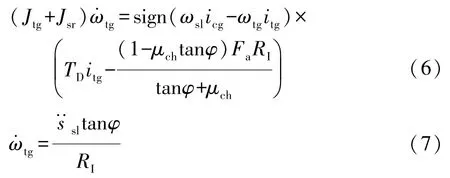
式中：Jsr为同步环的转动惯量；μch为齿间摩擦因数；φ为齿端角；RI为同步器接合套外齿的分度圆半径。

阶段5：第二次自由行程。在这个阶段，同步器接合套轴向移动以消除接合套外齿齿端与待接合齿轮齿圈齿端的轴向间隙。此阶段的动力学方程为

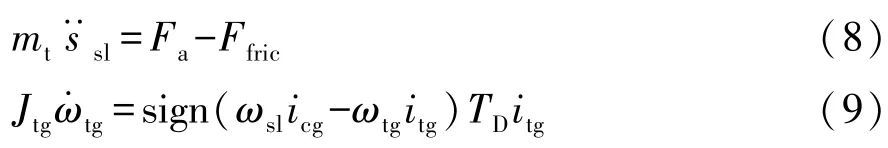
阶段6：同步完成阶段。在这个阶段，同步器接合套拨转待接合齿轮以完成整个同步过程。此阶段的动力学方程为

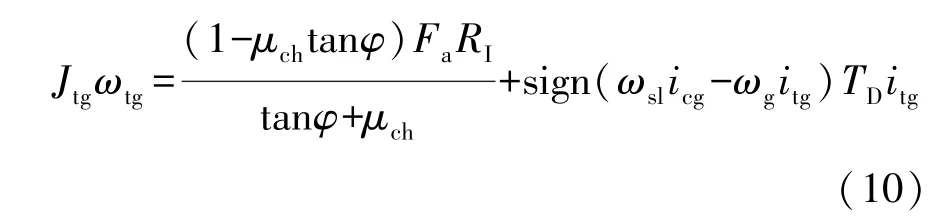
2 同步器自适应监控策略

一个动力系统如果既包含连续的动力学特性也包含离散的动力学特性，则该动力学系统是混合动态系统[10]。当某些离散事件发生时，连续的动力学特性与离散的动力学方程相互转换。

同步过程就是一个典型的混合动态系统。每一个阶段都是一个线性连续的子系统。但是阶段间的转换是离散的事件。

经典的控制方法在处理复杂的混合动态系统的控制问题上有不足。而监控理论(supervised control theory)已经被证明是一种有效处理混合动态系统的控制方法[11]。根据每个线性连续的子系统的动力学特性而开发相应的子控制器。而当某些特定的变量发生变化，即切换条件被满足时，监督模块(supervisor)将根据切换条件来选择相应的子控制器。因为切换的节点可根据切换条件的变化而改变，所以切换控制具有良好的自适应性和鲁棒性。图2为同步器监控系统的结构图。

图中，6个独立的子控制器和1个监督模块共享同样的输入和传感器信号。每个子控制器提供一个独立不相关的输出控制信号。监督模块根据特定的切换条件选择对应当前阶段的子控制器，当一个子控制器输出控制信号时，其他子控制器无法输出控制信号，避免引起控制逻辑错误导致错误操作。

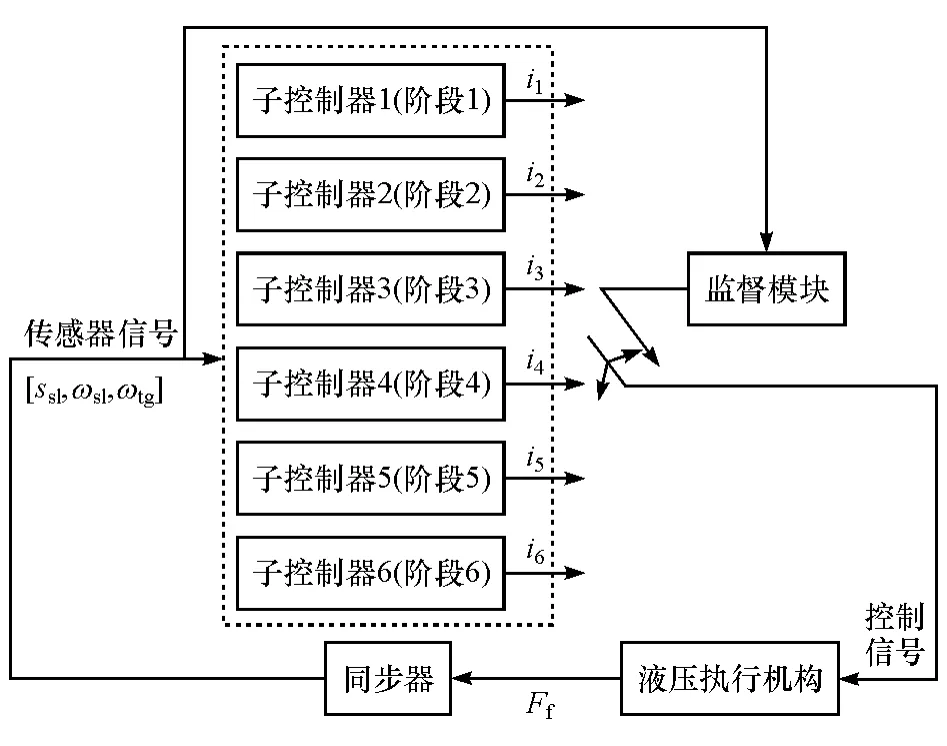
图2 同步器监控系统结构图

当监督模块识别到切换条件被触发时，新的子控制器将会代替当前的子控制器。在新子控制器的控制参数被采用时，控制信号可能会发生突变。为避免阶段转换之间控制信号发生不连续的突变，可限制控制信号的变化率。当控制电流变化率到达门限值时，控制电流将不会继续增加，而是保持不变。

2.1 各阶段子控制器

根据各阶段不同的动力学方程设计了相应的子控制器和控制目标轨迹。阶段1、阶段2和阶段5是直线运动，阶段3是旋转运动，阶段4和阶段6为混合运动阶段。

直线运动阶段控制器都是类似的，区别仅在于控制变量的参考值，采用PID闭环控制。控制目标为同步器接合套的速度，通过调整同步器接合套的速度与目标速度的差来实现闭环控制，控制原理如图3所示。

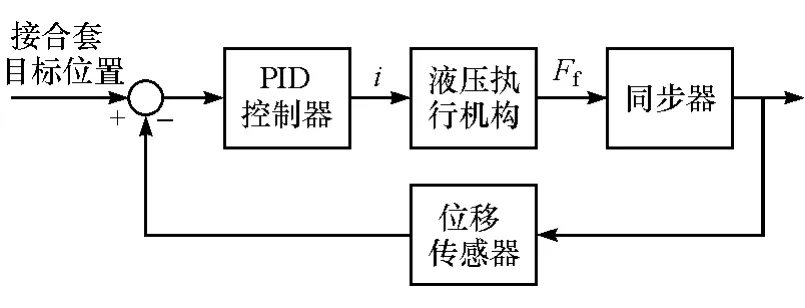
图3 直线运动阶段控制原理图

图4为阶段1和阶段2的目标位移。阶段5由于行程极短，无需设计单独的控制器，通过阶段4控制所带来的惯性即可完成。

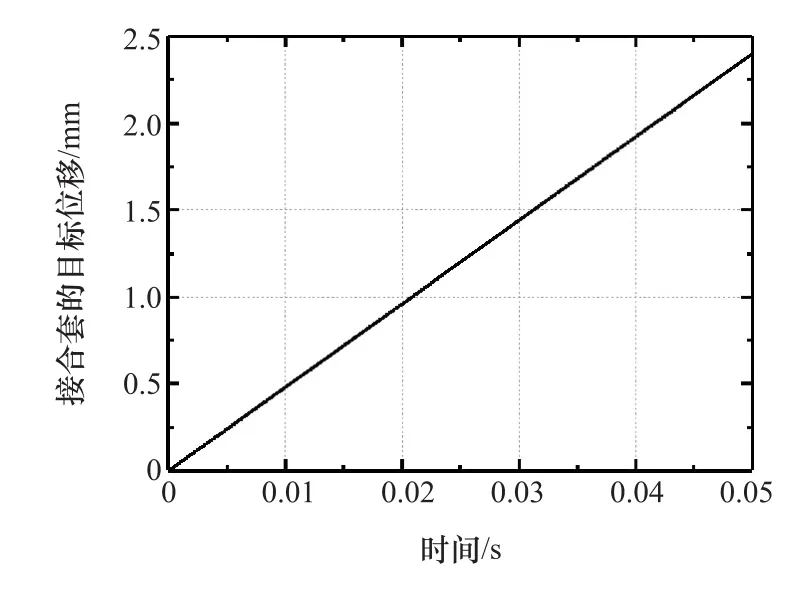
图4 阶段1和阶段2的目标位移

旋转运动阶段采用开环控制，根据式(5)同步阶段的动力学方程求得所需的同步力。

以升挡过程为例，将式(5)改写成式(11)，其中阻力矩TD可由经验值提供或根据实验估算出。

式中：t0为转速同步阶段开始时刻；t1为转速同步阶段结束时刻。

假设换挡同步力Fa和阻力矩TD在转速同步前阶段都不随时间而变化，则式(12)可进一步改写为

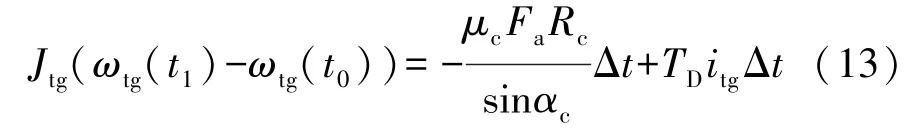
其中Δt=t1-t0

同步器的接合套和输出轴与整车相连，而整车的转动惯量相对较大，因此转速同步阶段同步器接合套的转速变化可以忽略，则可认为转速同步阶段结束时待接合齿轮的角速度ωtg(t1)与转速同步阶段开始时同步器接合套的角速度ωsl(t0)相同。式(13)左端可以改写成JtgΔω(t0)，换挡同步力Fa可以根据式(13)求出：

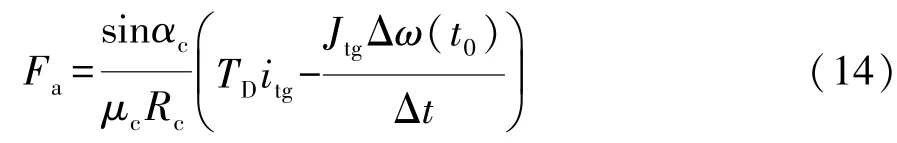
根据式(14)，只须确定所需的Δt，即可确定转速同步阶段所需的换挡同步力Fa。由于旋转阶段较为稳定，采用固定的Δt值，为100ms。

混合运动阶段指的是拨环阶段和接合套与待接合齿轮啮合阶段，这两个阶段具有类似的动力学特性，既存在轴向直线运动，又存在旋转运动。在混合运动阶段，轴向位移ΔX和周向位移ΔY的几何关系如图5所示。

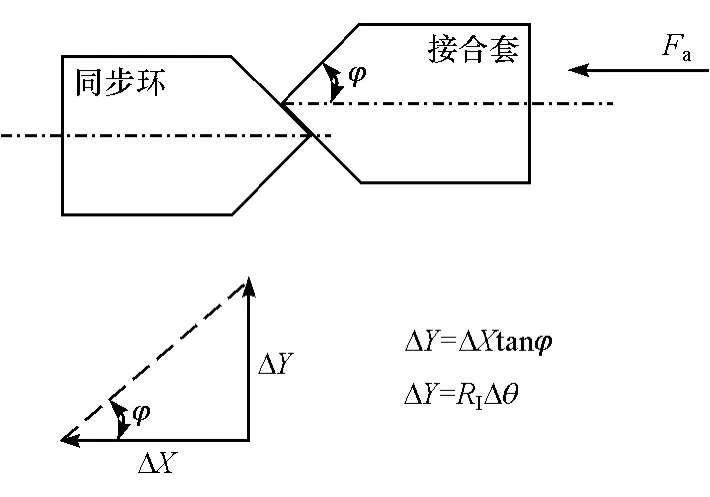
图5 混合运动阶段轴向位移ΔX和周向位移ΔY的几何关系

混合运动阶段，同步器接合套需要克服阻力矩才能顺利完成啮合，因此混合运动阶段的控制策略主要依据转矩平衡来制订。如果接合套产生的拨环力矩过小，不足以克服阻力矩，则会导致同步延迟甚至失败；如果接合套产生的拨环力矩过大，则会造成冲击。由以上分析可知，闭环控制比开环控制更适合混合运动阶段。但是闭环控制的问题在于如果混合运动阶段与前一阶段的控制信号幅值相差太多，会引起二次冲击。为解决二次冲击的问题，将混合运动阶段的闭环控制器分成两层来实现。第一层将换挡同步力调整至能平衡阻力矩的大小，第二层是以待接合齿轮转速为控制目标的闭环控制。分布式的结构可有效地解决二次冲击的问题。

2.2 切换条件

当切换条件被满足时就执行切换操作，从一个子控制器切换到另一个子控制器。当检测到某些状态变量的特定变化时，则认为相应的切换条件被触发，相应的子控制器被激活，而之前的子控制器则被关闭。

根据对同步过程的分析，不同阶段间的切换条件如表1所示。

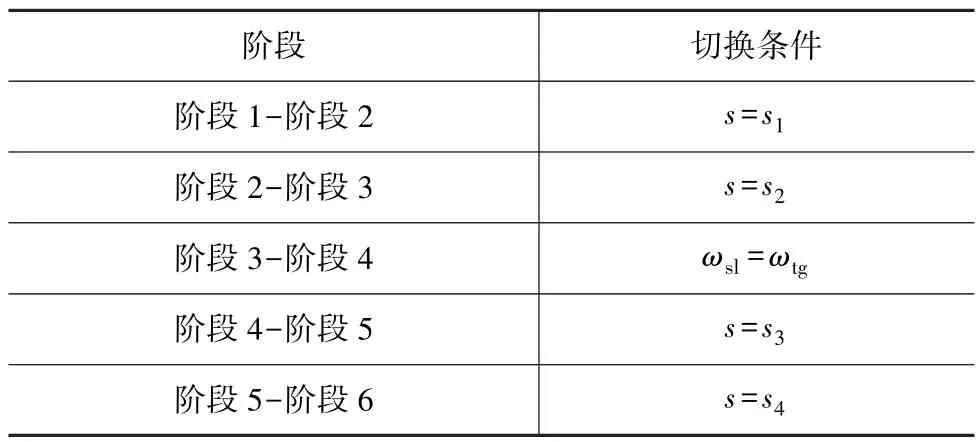
表1 监控各阶段间切换条件

阶段1是第一次自由行程阶段，因此阶段1与阶段2之间的切换条件为同步器位移s1，当同步器接合套轴向移动了s1就认为阶段一结束。阶段2是同步器接合套克服定位销阻力继续轴向移动的阶段，当同步器接合套进入锁止位置，则认为阶段2完成，因此阶段2与阶段3之间的切换条件为同步点s2。阶段3待接合齿轮转速与同步器接合套转速逐渐同步，直到两者转速相同，则认为阶段3完成，因此阶段3与阶段4之间的切换条件为ωsl=ωtg。阶段4为拨环阶段，同步器接合套将同步环拨转，直到同步器接合套与同步环啮合，当同步器接合套轴向移动了s3，则认为阶段4结束。阶段5为同步器接合套与待接合齿轮啮合阶段，同步器接合套拨转待接合齿轮直到同步器接合套与待接合齿轮啮合，因此阶段5与阶段6之间的切换条件为s=s4。

2.3 基于状态方程的切换条件

表1所示的切换条件并不具有自适应性，公差和磨损会导致同步器部件之间的初始相对位置发生变化，导致切换条件不再适用。

将前面推导的同步器各阶段动力学方程写成状态方程，阶段1的状态方程如式(15)所示。阶段2到阶段7的状态方程与阶段1的类似，不同的只是状态矩阵和输入矩阵。

其中

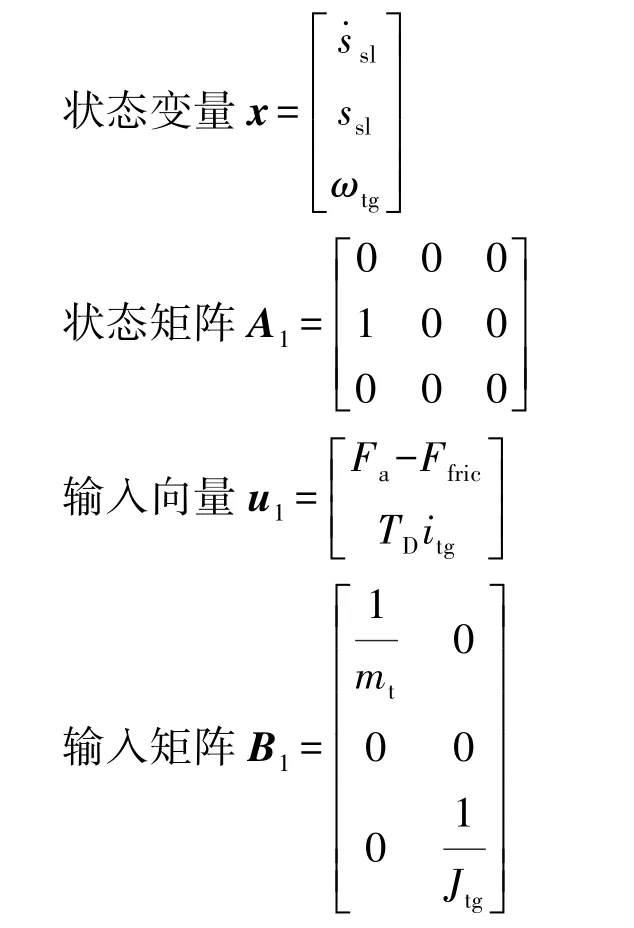
将控制输入代入各阶段的状态方程，可算出在该控制输入下的状态变量值，将计算出的状态变量的值x1，x2，…，x7与传感器测得的值相减，可以得到相应的误差en(n=1，2，…，7)：

对误差en取2-范数‖en‖2，根据其最小误差min(‖en‖)所对应的状态方程，则可确定当前同步器所处的阶段。由于同步过程各阶段的动力学特性区别很大，计算出的en也有较大的差异。

当同步器系统处于平动相阶段时，根据平动相状态方程计算出的状态变量xt与传感器测得的实际状态量在各维度上的误差都较小；而相同的控制输入代入转动相状态方程计算出的状态变量xr在各个维度上与实际状态量都存在较大误差：

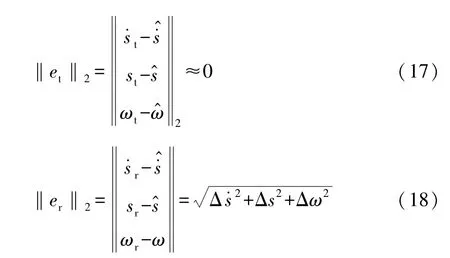
根据以上分析可知，将控制输入代入各阶段的状态方程计算出相应的状态变量，并与传感器测量值相减并取2-范数，2-范数最小的误差值所对应的状态方程即可确定同步器实际所处的阶段。

通过状态方程来判断同步器系统所处阶段，当对应最小的误差2-范数的阶段发生变化时，则认为切换条件被满足，系统从一个子控制器切换到另一个子控制器。

3 实验结果分析

为了评价同步器自适应监控策略，进行了实车实验。同步器接合套位移通过同步器拨叉上的永磁铁与变速器控制器中的霍尔传感器的相互作用来测量，如图6所示。

待接合齿轮的转速根据输入轴转速传感器测得的输入轴转速进行换算，同步器接合套转速根据输出轴转速传感器测得的输出轴转速进行计算。输入轴及输出轴转速传感器布置如图7所示。

图8为开环控制策略在2挡升3挡同步过程中的表现，各阶段的换挡同步力已提前标定好。

根据对整个换挡过程持续时间的要求，通常情况下整个同步过程的持续时间应小于250ms。而在此工况下，同步过程持续了约850ms，存在显著的同步延迟问题。由于开环控制策略为确保同步过程能完成，在同步时间超过一定限度的情况下会给出一个很大的脉冲命令，以确保同步器接合套不会被卡住而导致换挡同步失败，如图8(c)所示。

图6 永磁铁及变速器控制核心上的霍尔传感器

图7 输入轴及输出轴转速传感器的布置

由图8可见，阶段4和阶段6的持续时间最长，即拨环阶段和同步器接合套与待接合齿轮啮合阶段出现了同步延迟。原因是开环系统没有检测到阶段4已经完成，而是单纯地按照标定的换挡同步力来操作，如果该同步力未能克服传动系统中的阻力矩，同步器接合套就会被卡在原位无法继续轴向移动，无法顺利地完成拨环阶段和同步器接合套与待接合齿轮的啮合阶段。开环控制策略将输入轴处的阻力矩视为固定值，然而在很多工况下阻力矩都会大于该固定值。当阻力矩大于设计值时，换挡同步力无法克服阻力矩而使得同步器接合套无法轴向移动。

将同步过程监控策略应用于该工况，结果如图9所示。由图9(c)可见，混合运动阶段子控制器通过闭环控制将换挡同步力调整到合适的值，克服输入轴处的阻力矩，使得同步器接合套可顺利完成阶段4。阶段4的持续时间从图8中的约300ms降低到图9中的约30ms。整个同步时间从图8中的850ms降低到图9中的250ms左右。根据上述分析，监控通过计算切换条件来准确估计目前所处的阶段，并根据各阶段的子控制器来实现闭环控制，解决了同步延迟的问题，极大地改善了控制器性能。

由图8(c)和图9(c)的对比可见，同步过程监控阶段间控制信号过渡较好，没有控制信号突变发生，而开环控制策略没有限制控制信号的突变，在阶段4结束阶段出现了控制突变的情况，造成了二次冲击和噪声，影响了同步过程的平顺性，缩短了同步器零部件的寿命。

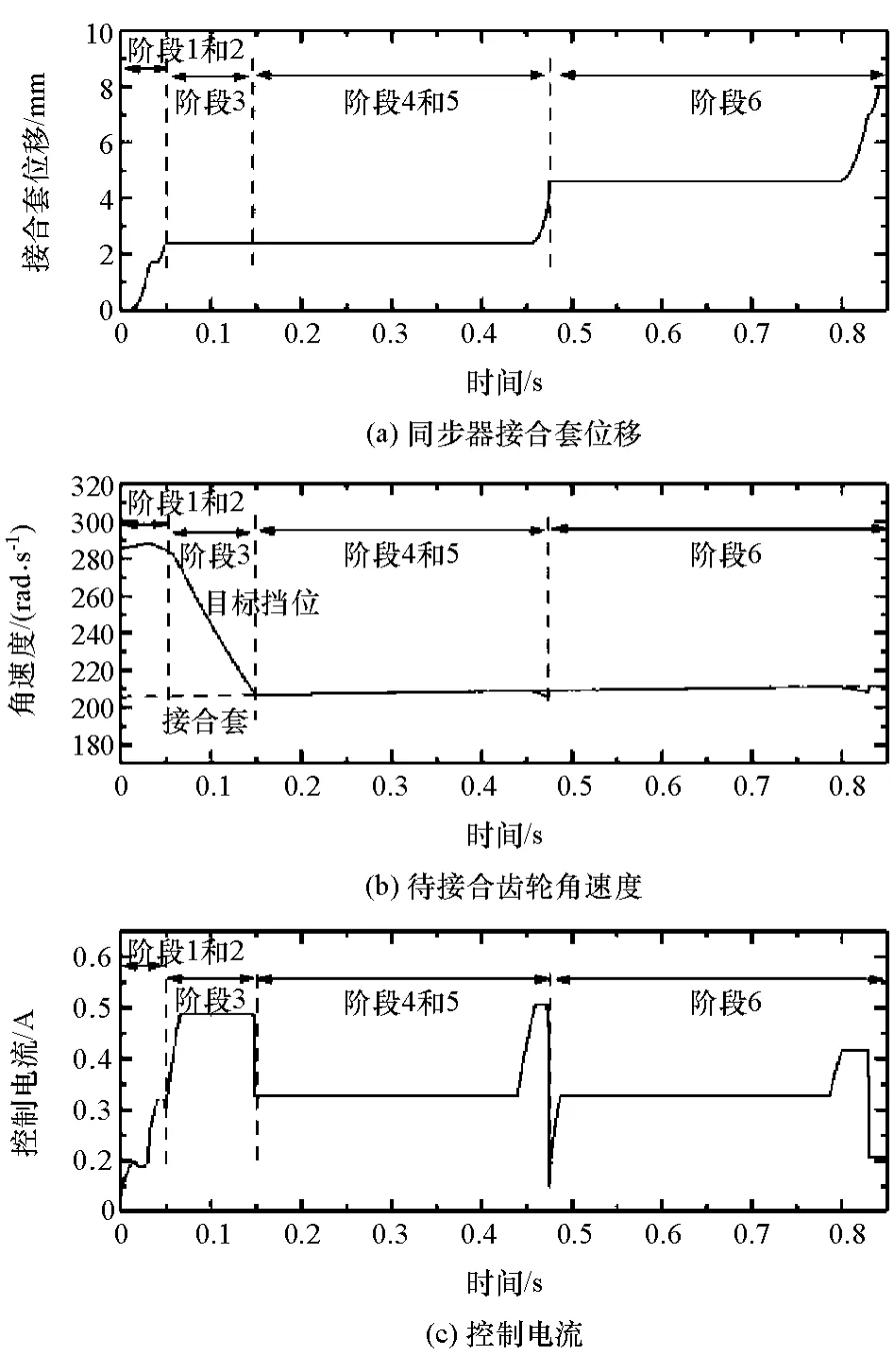
图8 升挡同步过程开环控制策略的表现

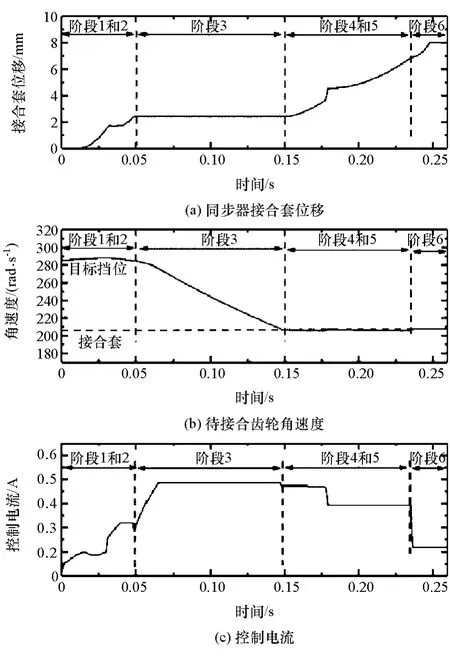
图9 升挡同步过程监控策略的表现

4 结论

本文中分析了双离合自动变速器同步过程，推导了同步器的数学模型，并根据同步过程的非线性特点提出了一种新的监控策略，针对不同的阶段设计了对应的子控制器，并根据状态方程给出了各阶段间的切换条件。对该控制策略进行实车实验，结果表明，该控制策略将同步过程的时间控制在250ms左右，优于现有的开环控制策略，改善了双离合自动变速器同步器的工作效率，有着很好的工程实用性。

[1] GALVAGNO E，VELARDOCCHIA M，VIGLIANI A.Dynamic and kinematic model of a dual clutch transmission[J].Mechanism and Machine Theory，2011，46：794-805.

[2] RAZZACKI S T.Synchronizer design：a mathematical and dimensional treatise[C].SAE Paper 2004-01-1230.

[3] LOVAS L，PLAY D，MARLALLGETI J，et al.Modelling of gear changing behaviour[J].Periodica Polytechnica Transportation Engineering，2006(1-2)：35-38.

[4] LOVAS L，PLAY D，MARLALLGETI J.Mechanical behaviour simulation for synchromesh mechanism improvements[J].Proceedings of Institution of Mechanical Engineers，Part D：J.Automobile Engineering，2006，220(7)：919-945.

[5] RAZZACKI S T，HOTTENSTEIN J E.Synchronizer design and development for dual clutch transmission(DCT)[C].SAE Paper 2007-01-0114.

[6] WALKER P D，ZHANG N.Investigation of synchronizer engagement in dual clutch transmission equipped powertrains[J].Journal of Sound and Vibration，2012，331(6)：1398-1412.

[7] WALKER P D，ZHANG N.Engagement and control of synchroniser mechanisms in dual clutch transmissions[J].Mechanical Systems and Signal Processing，2012，26(1)：320-332.

[8] WALKER P D，ZHANG N，ZHAN W Z，et al.Modelling and simulation of gear synchronisation and shifting in dual-clutch transmission equipped powertrains[J].Proc IMechE，Part C：J.Mechanical Engineering Science，2013，227(2)：276-287.

[9] GUSTAVSSON A.Development and analysis of synchronization process control algorithms in a dual clutch transmission[D]. Linkopings University，Sweden，2009.

[10] SCHAFT A J V D，SCHUMACHER H.An introduction to hybrid dynamical systems[M].Germany：Springer-Verlag，2013.

[11] HILHORST R A，AMERONGEN J V，LÖHNBERG P，et al.A supervisor for control of mode-switch processes[J].Automatica，1994，30：1319-1331.

Development of Monitoring Strategy for Synchronizer in Dual Clutch Transmission

Li Hongkui，Lu Tongli＆Zhang Jianwu
School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai200240

Due to the complexity of the synchronization process of dual clutch transmission，open loop control strategy can't achieve good effects.For improving the control performance of synchronizer，the synchronization process is divided into six phases for detailed analysis.The mathematical model for each phase is set up，and a monitoring strategy for synchronizer model is proposed based on the dynamic features of synchronizing process.The displacement of engaging sleeve and the rotating speeds of input and output shafts are substituted into the dynamics equation for each phase to estimate the phase of synchronizer，and different sub-controllers are designed for controlling the shifting force in each phase.The results of real vehicle comparative test show that the monitoring strategy proposed can effectively reduce synchronizing delay and the reverse effects of secondary shock，highly worthy of engineering application.

dual clutch transmission；synchronizer；monitoring strategy

∗国家自然科学基金(51175326)资助。

原稿收到日期为2016年2月25日，修改稿收到日期为2016年5月20日。

鲁统利，副教授，博士，E-mail：tllu＠sjtu.edu.cn。

10.19562/j.chinasae.qcgc.2017.02.011