基于双层规划的快速路与周边路网协调优化

武可心，傅白白，2，3*，岳贤飞

（1.山东建筑大学交通工程学院，山东济南250101；2.山东建筑大学建筑城规学院，山东济南250101；3.山东建筑大学交通研究所，山东济南250101）

基于双层规划的快速路与周边路网协调优化

武可心1，傅白白1，2，3*，岳贤飞1

（1.山东建筑大学交通工程学院，山东济南250101；2.山东建筑大学建筑城规学院，山东济南250101；3.山东建筑大学交通研究所，山东济南250101）

协调优化城市各等级道路系统，能有效促进其网络结构与资源的共享、合作与互补。文章在对快速路通道系统研究现状及已有优化理论方法分析的基础上，研究城市快速路出口匝道与周边路网衔接区域交通“瓶颈”产生的原因，以“交通压力均分、负荷转移”思想，建立以辅路分流为上层模型、以用户均衡分配为下层模型的双层规划模型，在模型中考虑了分流车辆绕行延误、交织延误以及受影响车辆运行延误等因素，最后给出算例。结果表明：优化后路网衔接区域交通“瓶颈”拥堵状况得到缓解，系统总延误大大降低，路网平均总延误相对不分流情况减少61%，相对固定分流情况减少50.1%；通过优化模型可获得辅路最优分流比例，结合算例，得出当出口匝道与辅路交通需求量为1500 pcu，且周边路网车道具有足够剩余通行能力时，其辅路分流比例可达0.9以上；当出口匝道及辅路交通需求超过1500 pcu，且受周边路网通行能力限制时，辅路分流比例随着辅路交通量与匝道交通量的增大而减小。

城市快速路；出口匝道；路网；双层规划；辅路分流

0 引言

城市快速路在城市道路系统中等级最高，具有较大的设计通行能力，它承载着城市各个区间主要的交通运输任务，其畅通与否关系着整个道路系统的运行效率，也逐渐成为解决交通问题的主要方法之一。然而，由于快速路上出入口匝道的存在，使其与周边路网相互衔接、相互影响，易形成交通“瓶颈”。因此，该“瓶颈”区域已成为国内外学者研究的重点。

Wu等以先进的交通管理系统ATMS（Advanced Traffic Management System）为基础构建了包括匝道控制、相邻交叉口信号控制和快速路分流等控制的整合优化模型及其算法步骤，但所构建模型与实际交通条件不符合且太复杂，在线控制较难［1］。杨晓芳等以城市快速路与相邻交叉口为研究对象，提出以总行程时间最短为目标函数，以最佳占有率、速度限制等为约束条件对出、入口匝道进行控制，但并未给出具体模型及算法［2］。Kwon等提出了匝道与相邻交叉口自适应的协调控制方法，使之达到操作平衡，但其文献中对具体的控制方法及应用实施并没有作具体介绍［3］。尹胜超等在协调控制方面，针对国内城市快速路出入口间距较短，且匝道出口经常毗邻城市道路平面交叉口的特点，给出自适应与协同信号控制策略的具体分配方案［4］。晏秋提出快速路与常规道路两系统基于阻塞指数的分层启发式方法进行整合协调控制，并对不同交通状态下的控制优化目标进行讨论，但模型中参数还需进一步研究［5］。黄琪提出快速路通道交通管理与控制的方法，构建静态、动态交通分流模型，并研究交通监控、交通诱导和信息发布等智能交通技术，但模型适用范围较小［6］。王立明研究了快速路匝道与衔接交叉口触发式协调控制策略与算法，并利用VISSIM仿真软件进行测试，但所提出模型仅适用于带辅路的菱形立交衔接形式，能否用于其他衔接方式还需进一步研究［7］。张苗主要研究单入口匝道与相邻交叉口协调控制，但对其交通状态划分比较简单，没有具体地考虑入口匝道与交叉口之间交通状态的相互影响［8］。上述研究多在快速路通道（快速路通道是由快速路主路、出口匝道、辅路以及相邻主干道组成）优化方面取得了一定的成果，但大多数文献未给出具体模型及有效算法，仅给出大致的想法，或所构建模型复杂难解，在线应用价值低。

由于快速路通道优化决策过程涉及了管理部门和公众的相互作用，而双层规划是具有两个不同目标层次的系统规划与管理问题［9-10］，可以同时考虑全局和个体双方的利益，因此双层规划可成为描述交通网络优化问题的理想工具。文章则利用双层规划基本原理，研究快速路出口匝道与周边路网协调优化问题，从均衡道路资源角度出发，以“交通压力均分，负荷转移”的思想建立双层规划模型。

1 快速路与周边路网问题描述

快速路与其他城市道路耦合不佳而造成的交通拥堵问题，其主要原因就是出口匝道与地面道路衔接处存在两股特性差异很大的交通流相互交织融合，车辆在交汇区争夺通行权，造成车流运行不畅［11］，形成交通“瓶颈”，不可避免的使该衔接区域引发交通问题，导致系统运行效率降低。因此，亟需对快速路系统与其周边路网协调优化，合理控制、管理出入口匝道及周边路网车辆，充分利用各等级道路资源，从而提高整个交通运输系统的运行效率。

快速路出口匝道车流与辅路车流在“瓶颈”H处汇合（H是合流路段；辅路是与快速路出口匝道直接相连的一般城市道路），如图1所示。在合流区H通行能力一定的情况下，来自辅路和出口匝道的车流汇至于此，如果这两股车流的交通需求总量超过合流段的最大通行能力，就会造成辅路和出口匝道的排队。在高峰时期，若辅路和出口匝道的车流量较大，一旦“瓶颈”处的车流消散与到达无法达到平衡，排队就会不断累积延伸，出口匝道的车流甚至会回溢到快速路主路［6］，影响主路车辆的运行。因此，造成出口匝道与其周边道路产生交通“瓶颈”的主要原因是合流路段的通行能力不能满足交通需求的总量。

图1 出口匝道与辅路交通“瓶颈”简图

一般情况下，并不是所有的城市道路都在同一时间拥堵，而是一部分拥堵，另一部分畅通，因此，合理利用道路资源，使车辆均衡地分配在道路网上，能够有效地缓解交通拥堵现象。城市快速路是整个道路系统中等级最高的，其运行效率远比其他城市道路要高，因此，在对快速路与其他城市道路整合优化时，需将快速路放在首位，保证其畅通运行。

不同交通流状态下，辅路分流比例不同。当出口匝道和辅路车流量较小，车辆运行顺畅，无需对辅路车辆进行分流。当车流量增大，车辆运行受阻出现排队现象时，辅路车流和出口匝道车流总量超过合流交织区的通行能力，则优先满足快速路出口匝道的交通需求，对辅路进行分流，将一部分车辆引导到周边路网上，使合流区的通行能力更多地分配给出口匝道，避免其排队回溢影响快速路主路车辆行驶，促使各条道路车辆运行平稳、顺畅，如图2所示。

图2 辅路分流简图

2 双层规划模型构建

文章中上层优化模型是从交通管理者的角度出发，确定合适的辅路分流比例，实现路网系统的总延误最小；下层规划模型则是从路网使用者的角度出发，通过寻找最短路径来实现用户最优［9］。上层模型的辅路分流量影响下层模型的交通流分配，下层模型的路网容量又制约上层模型分流比例的大小。

2.1 模型假设

（1）出口匝道与辅路交通量始终不大于自身道路通行能力；

（2）出口匝道下游快速路主线不存在交通瓶颈；

（3）出口匝道周围存在未被完全利用的城市道路，且在辅路分流初期周边路网车道具有足够的剩余通行能力；

（4）周边路网交叉口信号配时为固定式配时，且初始时刻车辆排队长度为零［12］；

（5）快速路出口匝道和辅路车辆平均到达率是稳定不变的。

2.2 目标函数确定

2.2.1 上层目标函数确定

上层优化模型中由于辅路分流车辆绕行，致使车辆运行距离增加，产生绕行延误，另外分流车辆因绕行汇入其他道路时，需等待车道上车辆间隙，增加汇入延误；汇入后，对该车道上初始状态下行驶的车辆产生影响而增加其交织延误。为简化问题，假设分流绕行车辆在上述几个行驶状态中忽略加、减速过程，即车辆在某一状态持续的时间是行驶距离和行驶速度的比值，而与车辆的加速度无关［13］。

综上所述，系统的总延误Dz等于辅路分流车辆绕行产生的总延误trz（包括绕行车辆绕行延误dr、汇入时等待延误ds以及受绕行车辆影响的车辆延误dj）与其他未被利用的道路上车辆运行延误Da之和，用式（1）表示为

（1）分流车辆绕行总延误trz

①分流车辆绕行及交织延误

车辆绕行延误与绕行距离和车速有关，车辆交织延误与交织长度和交织速度有关。交织车辆的速度与交织强度有关，由式（2）表示为

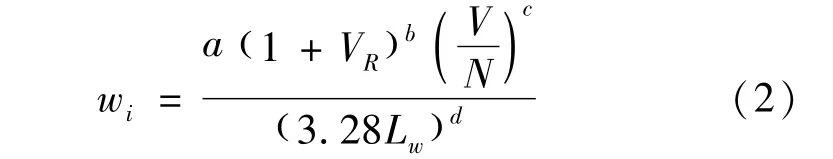
式中：i为车流类型，包括交织车流和非交织车流；VR为交织区内交织流量和总流量的比；V为交织区总流量；N为交织区内总车道数；Lw为交织区长度；a、b、c、d为标定的常数，可查HCM2000［14］获得。

交织或非交织车流的平均车速由式（3）表示为

式中：vff为自由流车速，可由道路等级获得。

由绕行距离Lrx、交织长度Lw、交织速度vi，可计算分流车辆绕行及交织延误dr由式（4）表示为

②分流车辆汇入时等待延误

辅路分流车辆绕行到其他道路上时需要等待车辆空隙才能汇入，其等待延误［15］由式（5）表示为

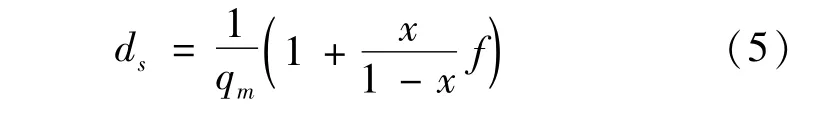
式中：x为分流车辆汇入饱和度；f为修订参数，值取1；qm为绕行车辆最大汇入量，由式（6）表示为

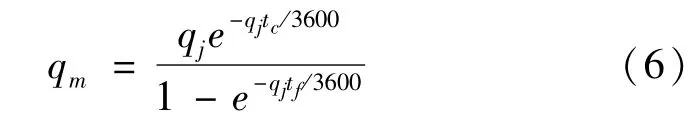
式中：qj为与绕行车辆冲突的车流量；tc为临界间隙，取4 s；tf为车头时距，取2 s。

③受绕行车辆影响的车辆延误

辅路分流车辆绕行到其他车道，会对该道上初始状态下非绕行车辆造成影响，其延误主要来源于因受绕行车辆变道影响而产生的车速降低。因此，受绕行车辆变道影响的车辆延误dj由式（7）表示为

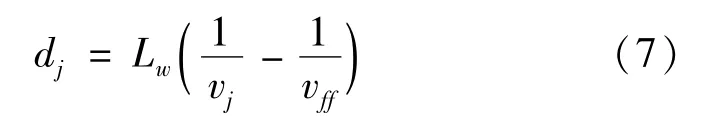
式中：vj为受交织影响车辆在交织区的平均车速。

因此，辅路分流车辆绕行总延误由式（8）表示为

式中：qf为辅路分流车辆，pcu。

（2）未被利用的道路上车辆运行延误Da

车辆在道路上的运行延误等于车辆实际旅行时间与理想旅行时间之差。车道交通状况根据道路服务水平进行划分，不同服务水平下，其运行速度不同。

道路交通延误的计算公式由式（9）表示为

式中：a为路段；n为路段数；Da为路段a上车辆运行延误；TaR为路段a当前交通状况下车辆旅行时间；Ta0为路段a自由流状况下的车辆旅行时间；La为路段a长度；VaR为车辆当前运行速度；Va0为车辆自由流速度。

2.2.2 下层目标函数确定

下层规划模型的目标函数是所有路段阻抗函数积分求和之后取最小值，其目的是找出路网平衡时所对应的各路段交通流量，计算交通起讫点OD（Origin Destination）间的最短路径，使其阻抗最小。

2.3 优化模型建立

上层规划模型以快速路出口匝道和辅路的交通需求为控制变量，以整个路网中各交通设施的通行能力为约束条件。采用将一部分辅路车流转移到周边路网上去，构建动态交通分流模型，模型以路网上所有车辆的总延误最小为评价指标，确定合理的辅路分流比例。

下层规划模型是标准的用户平衡分配模型，描述不同辅路分流比例设置方案下出行者的路径选择行为［16］。由于上层模型中辅路车辆的分流，使周边路网上的交通量有一定的改变，这将打破原有路网的交通平衡［17］，在下层规划模型中，出行者根据路网车流量的变化，估算不同路径阻抗大小，然后选择阻抗最小路径，最终在路网上形成新的交通流量。

上层规划模型形式由式（10）～（14）表示为

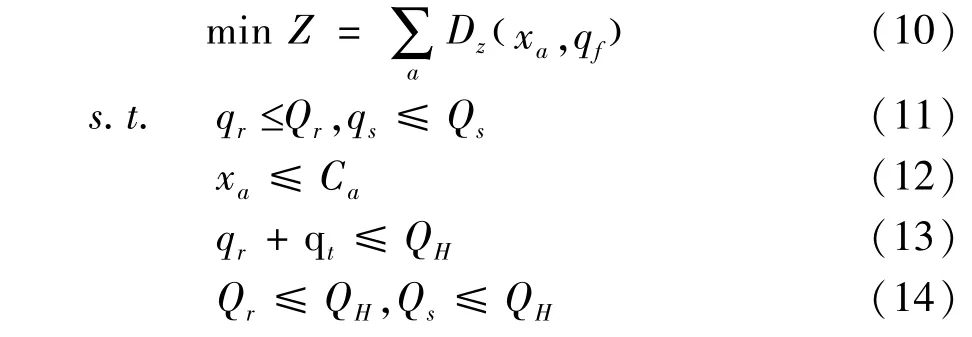
式中：qr为快速路出口匝道车流量，pcu；Qr为快速路出口匝道通行能力；qs为辅路车流量，pcu；Qs为辅路通行能力，pcu/h；Ca为路段a的通行能力，pcu/h；qt为辅路分流后车道上剩余车量，pcu；QH为合流交织段通行能力，pcu/h；qf为辅路分流车辆，pcu；Lr为快速路出口匝道排队长度，km；Dz为系统总延误，s。xa为路段a上的交通量，pcu，其满足下层规划模型，由式（15）～（18）表示为

式中：ta()x为路段a上的阻抗，s；frsk为出发地为r、目的地为s的OD间的第k条径路上的流量；δrsa，k为路段、路径相关变量，即0-1变量，如果路段a属于从出发地为r、目的地为s的OD间的第k条路径，则为1，否则为0；qrs为出发地r和目的地s之间的所有径路的集合。

3 算例分析

如图3所示，路网中共9个节点，15条路段，路段上标注分别表示路段编号与长度。路段11和路段15为单向车道，其他13条路段均为双向车道。网络中有6个OD对，分别为：q1，3、q1，5、q2，4、q3，1、q4，2、q5，2，匝道、辅路交通需求与车辆运行速度根据道路等级不同由道路通行能力手册［14］查询得到。

图3 算例网络结构图

根据文章所提出模型，由粒子群算法和方向搜索法对其求解［18］，计算出口匝道与辅路不同交通需求下辅路分流比例。利用Matlab软件画出的匝道、辅路交通量与辅路分流比例三维关系图，如图4所示。为使图形更明显地表现出三个变量之间的关系，图中只给出交通量大于1500 pcu的辅路分流比例。

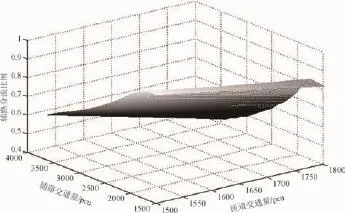
图4 辅路分流比例图

从图4可看出，辅路分流比例随着辅路交通量与匝道交通量的增大而减小。当出口匝道与辅路交通需求量为1500 pcu，且周边路网车道具有足够的剩余通行能力时，其辅路分流比例可达0.9以上；因合流段必须首先满足匝道交通需求，当出口匝道交通量不断增大时，分配给辅路的交通量就越少，辅路排队情况愈严重，理论上需要分流的车辆应该增加，但受周边路网道路通行能力限制且需保证系统总延误最小，结果导致辅路分流比例减小。

图5 总延误对比图

从图5分析可知，不分流与固定分流两种情况下车辆总延误与辅路、出口匝道的交通需求基本呈正相关关系。当辅路与出口匝道交通需求不超过合流区通行能力时（如编号1～8），三种情况下车辆总延误基本相同。当辅路与出口匝道交通需求超过合流区通行能力时，不分流车辆总延误最大，按文章所提出模型分流后车辆总延误最小。车辆不分流情况下，当出口匝道与辅路交通量超过合流区通行能力时（如编号13～18），系统总延误增长率加快，然后趋于平稳；编号30～31处由于合流段出现严重交通堵塞，车辆基本处于停滞状态，导致总延误急剧增长的现象。车辆固定分流情况下，系统总延误分布趋势与不分流情况相似，但平均总延误较小。车辆按模型分流，系统总延误在辅路开始分流情况下呈下降趋势（如编号8～13）；随着交通量不断增加，路网车流不再处于自由流状态，车辆运行延误增加（如编号13～30）；编号30～31处延误量急剧增加，是由于受周边路网通行能力限制，辅路分流量较小，导致合流区交通拥堵，车辆运行受阻。

4 结论

通过上述研究可知：

（1）辅路分流优化方法可以有效缓解城市快速路出口匝道与周边路网衔接区域交通“瓶颈”拥堵问题，使系统总延误大大降低。通过算例分析，按模型分流平均总延误相对不分流平均总延误降低61%，相对固定分流平均总延误降低50.1%。

（2）当出口匝道与辅路交通需求量为1500 pcu，且周边路网车道具有足够剩余通行能力时，其辅路分流比例可达0.9以上；当出口匝道及辅路交通需求超过1500 pcu时，因合流段必须首先满足匝道交通需求，分配给辅路的交通量就越少，辅路排队情况愈严重，理论上需要分流的车辆应该增加，但受周边路网道路通行能力限制且需保证系统总延误最小，结果导致辅路分流随着辅路交通量与匝道交通量的增大而减小。

［1］ Wu J.F.，Chang G.L..An integrated optimal control and algorithm for commuting corridors［J］.International Transportation on Operational Research，1999，6（1）：39-55.

［2］ 杨晓芳，付强，杨晓光.城市快速路与地面道路交通整合控制分析［J］.交通与计算机，2005，23（5）：4-7.

［3］ Kwon E.，Ambadipudi R.P.，Bieniek J..Adaptive coordination of ramp meter and intersection signal for optimal management of freeway corridor［C］.Washigton：The 82th Annual Meeting of Transportation Research Board Meeting，2003.

［4］ 尹胜超，许润民，张毅.城市快速路瓶颈区域控制策略研究［J］.交通运输系统工程与信息，2012（2）：27-33.

［5］ 晏秋.城市快速路街接问题系统研究［D］.成都：西南交通大学，2012.

［6］ 黄琪.城市快速路出口匝道及其周边路网区域交通控制与管理方法研究［D］.武汉：华中科技大学，2014.

［7］ 王立明.快速路匝道与衔接交叉口触发式协调控制方法研究［D］.长春：吉林大学，2009.

［8］ 张苗.城市快速路入口匝道与衔接交叉口协调控制方法研究［D］.西安：长安大学，2011.

［9］ 王中芳.城市动态路网优化及交通流分配模型与算法研究［D］.西安：西安建筑科技大学，2011.

［10］秦进，倪玲霖，董龙云，等.考虑可持续发展的交通网络设计双层模型与算法［J］.交通运输系统工程与信息，2010，10（4）：111-117.

［11］郝媛，徐天东，干宏程，等.城市快速路交通流特性研究［J］.交通信息工程与信息学报，2006，4（4）：21-27.

［12］李爽爽.城市快速路出口匝道辅路控制参数优化方法研究［D］.长春：吉林大学，2007.

［13］邓明君，曲仕茹，秦鸣.基于延误的U-turn交通组织可行性分析方法［J］.公路工程，2014，39（6）：119-123.

［14］Paul R.，Mark V.，Lily E..Highway Capacity Manual 2010［M］.Washington：New TRB Publication，2010.

［15］王殿海.交通流理论［M］.北京：人民交通出版社，2002.

［16］Liu H.，He X.，He B..Method of successive weighted averages and self-regulated averaging schemes for solving stochastic user equilibrium problem［J］.Networks and Spatial Economics，2009，9（4）：485-503.

［17］赵顺晶，龙建成.通勤廊道换乘停车费用优化模型及算法［J］.系统工程理论与实践，2016，36（9）：2337-2344.

［18］杜培全.混合交通网络设计双层优化模型及其求解算法研究［D］.南京：东南大学，2010.

Expressway and surrounding road network coordinated optim ization based on bi-level programm ing

Wu Kexin1，Fu Baibai1，2，3*，Yue Xianfei1
（1.School of Transportation Engineering，Shandong Jianzhu University，Jinan 250101，China；2.School of Architecture and Urban Planning，Shandong Jianzhu University，Jinan 250101，China；3.Transportation Institute，Shandong Jianzhu University，Jinan 250101，China）

The coordinated optimization of each grade road system can effectively facilitate the sharing，cooperation and complementof the network structure and resources.On the basis of analyzing research status and existing optimization theoreticalmethod of expressway tunnel system，this paper researches the reasons for the connection regional traffic“bottleneck”between urban expressway offramp and surrounding road network，establishes a bi-level programmingmodel of the uppermodel for side road traffic diversion and the lowermodel for user equilibrium assignment，which is based on the thought of“divide traffic pressure，load transfer”.Themodel considers some factors such as routing delay of distributed vehicles，interleaving delay and running delay of effected vehicles，and also gives a numeric example.The results show that the congestion of connection area traffic“bottleneck”is relaxed and the total system delay decreases substantially in the optimized-network，the average total delay of road network decreases significantly and its relatively non shunt decreases by 61%，and its relatively fixed shunt decreases by 50.1%.According to the proposed model，we can obtain the optimal diversion ration of auxiliary road.Finally，by combining the numeric example，the optimaldiversion ration of auxiliary road can reach more than 0.9 when the off-ramp and side road traffic demand is1500 pcu，and the surrounding road network laneswith sufficiently surplus capacity.When the traffic demand of off-ramp and side road surpasses1500 pcu and restricted by the surrounding road network capacity，the auxiliary road diversion ration decreaseswith the increase of auxiliary road and off-ramp traffic volume.

urban expressway；off-ramp；road network；bi-level programming；auxiliary road diversion

U491

A

1673-7644（2017）01-0033-06

2016-12-13

国家自然科学基金资助项目（71171124，71371026，71471104）

武可心（1991-），女，在读硕士，主要从事交通运输规划与管理等方面研究.E-mail：305685173＠qq.com

*：傅白白（1961-），女，教授，博士，主要从事城市交通规划理论与方法等方面研究.E-mail：fubaibai＠163.com