高中数学圆锥曲线教学的分析与研究

江苏省启东中学 蔡 罡

高中数学圆锥曲线教学的分析与研究

江苏省启东中学 蔡 罡

解析几何作为高中数学中的重要组成部分，对学生空间思维、抽象思维以及逻辑思维的培养和强化能够起到关键性的作用。本文将以高中数学圆锥曲线的相关知识为基础，分析当下高中数学几何教学的现状和存在的问题，并提出一些改进方案，以达到提高圆锥曲线教学质量的目标。

高中数学；圆锥曲线；解析几何

圆锥曲线是高中数学几何教学中的重点内容，因其对学生各方面思维能力均有较高要求，所以学生在学习圆锥曲线的相关知识时能够明显感受到一定的难度和阻力。本文将针对这样的现象，着重分析目前高中数学中的圆锥曲线教学存在的问题，并研究出解决这些问题的策略。

一、高中数学圆锥曲线的教学现状分析

1.高中生对数学的观念及学习数学的态度

学习态度在很大程度上影响着学生学习知识的效果。因圆锥曲线知识的重要性显著，所以这部分知识的难度也是可想而知的。高考数学中，与圆锥曲线相关的知识常被放在最后的三道大型综合题中进行考查，难度通常表现在图形复杂、动态问题以及计算繁杂等方面，这些都是学生在学习数学的过程中需要重点克服的短板问题。

学生在实际操练时看到的往往只是题目本身的含义，而没有深入地考虑问题内在的逻辑和普遍规律。在解决问题时，学生的最终目的大都是解出最终答案的数值，而很少有人主动深入探究问题，从多个层次、多角度地分析得出最适方法。实际上，高中数学圆锥曲线部分的知识与代数数学之间存在着不可分割的关系，但很多学生无法将两者有机结合，从而无法顺利构建圆锥曲线的知识体系。

2.教师在圆锥曲线教学中采取的方法和课堂的策略

当下高中数学教学的现状是教师总体围绕着两个中心任务进行教学，一方面是根据教学大纲的要求指导学生学习数学知识，另一方面，也是学生、家长以及教师最为关注的一个方面，即让高中数学教学紧密贴合高考升学要求。很多教师对圆锥曲线这一部分的内容非常重视，因为该部分将代数与几何知识结合得非常紧密，通常出现在高考数学的最后三道大题中，分量很重。

高中数学教学普遍存在为迎合高考而针对性教学的现象，教师所设计的课堂模式常常片面地围绕着高考得分的主题，采用以教师讲授为主的课堂模式给学生灌输知识、呈现重难点内容，接着进行“题海式”实际操练，这样的做法往往会造成学生出现“高分低能”的情况。此外，在教学方法上，教师常常会忽略学生课后思考和探究的重要作用，不能做到与学生进行知识掌握程度的沟通，忽略了学生发散性思维的培养和提升，仅仅讲解圆锥曲线的基本知识。

二、高中数学圆锥曲线的教学研究策略

1.进行互动探究性学习，打造良好氛围的课堂

学习是一个循序渐进的过程，所有的学习活动都处在一个大群体之中，相互影响，相互联系。圆锥曲线作为高中数学教学的一个重点和难点，其过程必定离不开师生间、生生间的交流合作以及互动探究。

例如，教师在讲授《曲线方程》这一章节的知识点时，课堂应当以教学目标为根据，再结合学生的能力和水平来设计，采用师生互动以及学生合作的方式来引导学生互助学习、共同进步。教师可以给出这道抛物线的经典例题：如图1所示，抛物线y2=4x，顶点是O，焦点是F，点P能在抛物线上随意移动，Q是OP的中点，M是FQ的中点，求出M点的轨迹方程。教师可将学生分为若干小组进行自主探讨。高中学生相对于初中和小学生来说相对自由，希望表达自己的看法、张扬个性。

本题解析如下：

解： 设M（x，y）,P（x1，y1），Q（x2，y2），易求得y2=4的焦点F的坐标为（1，0），

∵M是FQ的中点，

2.丰富教学的内容，开拓学生的思维

高中教材内容最鲜明的特点之一是每个章节之间既相互独立又相互联系，能够形成一个完整的知识框架体系。圆锥曲线这一章节的内容是高中数学教学的重要组成部分，也与其他章节的内容紧密相连，如代数方程等等。因此，教师在进行课堂设计时，需理清解析几何与其他章节知识点的关系。例如，可以设置复习题如下：

该题考查了椭圆未知参数以及范围的计算，考查了学生的发散性思维能力以及条件转化能力，需要学生具有较强的逻辑思维以及发散性思维，还需要严谨的转化能力。

本题解析如下：

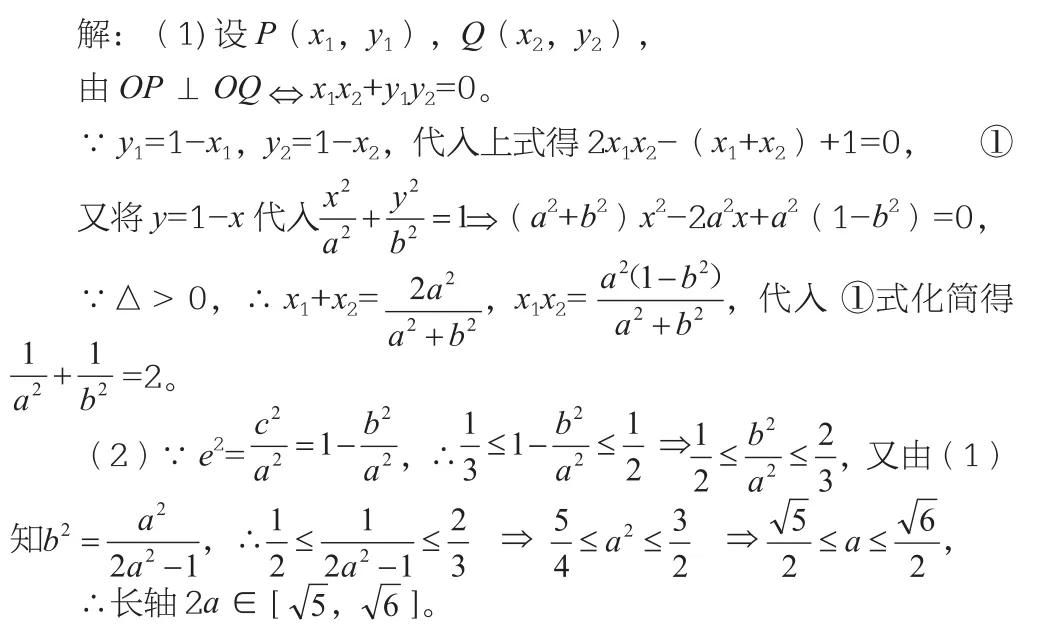
3.授予画图的方法解决数学问题

数形结合的思想是高中数学思想中最重要的组成部分之一，教师在圆锥曲线的教学中，应当注重培养学生数形结合的能力，提高学生对图象的熟悉和敏感程度。教师在讲解相关例题时，可结合具体图象，更为直观地将问题的关键点呈现出来。学生在刚接触圆锥曲线的相关知识时，对各种曲线的图象不甚了解，在解题时常常无从下手，因此图象可以起到帮助学生更好地理解题意的作用。

例如：设动点p到两点F1(-1，0)，F2（1,0）的距离分别为d1和d2，∠F1PF2=2θ，且存在常数λ，λ∈（0,1），使得d1d2sin2θ=λ。