局域均值分解和小波阈值在大地电磁噪声压制中的应用
李 晋,彭 冲,汤井田,燕 欢,蔡剑华
(1.湖南师范大学 物理与信息科学学院, 长沙 410081;2.中南大学 地球科学与信息物理学院, 有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;3.湖南文理学院 物理与电子科学学院, 湖南 常德 415000)
局域均值分解和小波阈值在大地电磁噪声压制中的应用
李 晋1,2,彭 冲1,汤井田2,燕 欢1,蔡剑华3
(1.湖南师范大学 物理与信息科学学院, 长沙 410081;2.中南大学 地球科学与信息物理学院, 有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;3.湖南文理学院 物理与电子科学学院, 湖南 常德 415000)
大地电磁测深法是基于电磁感应原理,利用天然交变电磁场来研究地下岩层的电学性质及其分布特征。然而,天然电磁场频带范围宽、信号微弱,在实际测量中大地电磁信号极易受到各种电磁噪声干扰,严重影响了后续的电磁法反演解释水平。针对这一难题,将局域均值分解(LMD)的自适应性和小波分析的多分辨性相结合,提出基于局域均值分解和小波阈值的大地电磁噪声压制方法。将含噪信号进行LMD分解得到若干阶乘积函数(PF)分量;根据大地电磁信噪特征保留PF1分量,仅对其余各阶PF分量选取合适的小波阈值进行降噪处理;叠加重构获得大地电磁有用信号。通过计算机模拟典型强干扰,研究不同小波函数、分解层数及阈值方式下算法的去噪性能,并将其应用于矿集区实测大地电磁数据处理。实验结果表明,所提方法能较好地提取出叠加在微弱大地电磁信号上的大尺度强干扰的轮廓特征,视电阻率曲线更为光滑、连续,低频段的大地电磁数据质量得到了明显改善。
局域均值分解; 小波阈值; 大地电磁; 噪声压制
大地电磁测深法(Magnetotelluric,MT)诞生于20世纪50年代,是一种以天然交变电磁场为场源,通过测量地表相互正交的电场和磁场,获得地下电性结构信息的地球物理方法。与有源的电磁勘探方法相比,天然大地电磁场频带范围宽且本身信号极其微弱,野外观测到的大地电磁信号不可避免地会受到各种噪声的污染[1]。尤其是在矿集区,随处可见的高压电网、广播电台、通讯电缆、信号发射塔、各种金属管网以及用于矿山开采的大功率直流电机车等严重影响了实测大地电磁信号的采集,大地电磁测深数据质量极具下降,阻抗估算偏差严重及测量获得的视电阻率值过度失真等状况导致不能客观反映地下电性分布[2]。为此,如何消除大地电磁信号中的噪声干扰、提高大地电磁测深数据质量是国内外长期瞩目并不断取得进展的研究课题。诸多现代信号处理方法,如Hilbert-Huang变换[3]、广义S变换[4]、方差比维纳滤波[5]、同步时间序列依赖[6]、数学形态滤波[7]、子空间增强[8]等均被应用到该领域,并在一定程度上对大地电磁测深数据质量起到了积极的改善作用,推动了MT法在与各种噪声竞争中不断成长。
局域均值分解(Local Mean Decomposition, LMD)是一种分析非线性、非平稳信号的时频分析方法,能自适应地将待处理信号分解为若干阶乘积函数(Production Functiion, PF)的线性组合[9];该方法已成功应用于机械故障盲源分离、滚动轴承故障诊断等领域[10-12]。小波分析法具有良好的时频分析和多分辨率分析能力,能较好地分析非线性、非平稳信号。本文根据大地电磁信号的特征,借助于机械振动中广泛使用的LMD法和小波分析法,将LMD的自适应性和小波分析的多分辨性相结合,提出一种基于局域均值分解和小波阈值的大地电磁噪声压制方法。通过对模拟信号和矿集区实测大地电磁数据进行仿真实验,结果表明该方法可用于压制矿集区典型大尺度方波和充放电三角波干扰,大地电磁测深数据质量得到了明显改善。
1 局域均值分解
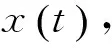
(1)
(2)

(3)
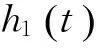
(4)
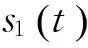
h1(t)=x(t)-m1(t)
h2(t)=s1(t)-m2(t)
⋮
hn(t)=sn-1(t)-mn(t)
(5)
式中:
s1(t)=h1(t)/a1(t)
s2(t)=h2(t)/a2(t)
⋮
sn(t)=hn(t)/an(t)
(6)
其中:迭代终止的条件为
(7)
(6) 将迭代过程中产生的所有局域包络估计函数ai(t)相乘,得到PF分量的包络信号,即瞬时幅值函数a1(t):
(8)
(7) 将包络信号a1(t)和纯调频信号sn(t)相乘,得到原始信号的第一个PF分量:
PF1(t)=a1(t)sn(t)
(9)
式中:PF1(t)包含了原始信号x(t)中最高的频率成分,且是一个单分量的调幅-调频信号;瞬时频率f1(t)可由纯调频信号sn(t)求出,即:
(10)
(8) 将原始信号x(t)减去第一个PF分量PF1(t),得到一个新的余量信号r1(t),并将r1(t)作为新的输入数据重复上述步骤、循环k次,直到rk(t)为单调函数:
r1(t)=x(t)-PF1(t)
r2(t)=r1(t)-PF2(t)
⋮
rk(t)=rk-1(t)-PFk(t)
(11)
经过上述步骤,原始信号x(t)被分解为k个PF分量与rk(t)之和:
(12)
图1所示为仿真信号x(t)的时域波形及LMD分解效果图,x(t)的表达式如下:
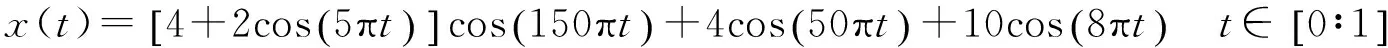
(13)
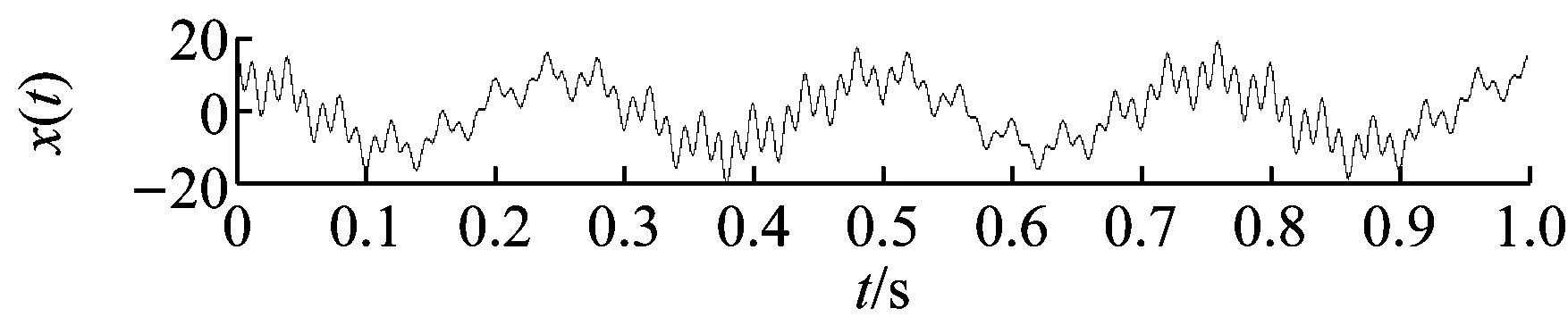




图1 x(t)的LMD分解效果Fig.1 LMD decomposition effect of x(t)
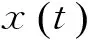
2 小波阈值选取及阈值去噪
小波变换的实质是信号在小波基空间进行分解,小波基空间则由选定的小波母函数经过伸缩和平移构成。
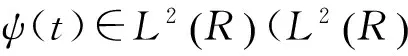
(14)
将ψ(t)平移和伸缩可得到一组小波序列,对于连续情况小波序列表示为
(15)
式中:a为伸缩因子;b为平移因子。

(16)
其逆变换表示为
(17)
小波阈值的选取方式主要有选择启发式阈值(Heursure)、极小极大方差阈值(Minimaxi)、基于Stein无偏似然估计阈值(Rigrsure)和固定阈值(Sqtwolog)四种方式,其阈值函数可分为软阈值函数和硬阈值函数两种情况。
小波阈值去噪的基本步骤如下:
(1) 选择与噪声形状相似的小波函数和合适的分解层数,将待处理信号进行小波变换得到分解后的小波系数;
(2) 利用不同的阈值选取方式确定阈值,选取合适的阈值函数(软、硬阈值)对各层小波系数进行量化处理;
(3) 对新得到的小波系数进行重构,获得去噪后的信号估计。
3 仿真信号分析
观测矿集区海量实测大地电磁数据可知,时间域波形中通常出现大尺度方波和充放电三角波干扰[16-17]。为此,计算机模拟典型的大尺度方波和充放电三角波干扰进行仿真实验。降噪性能采用曲线相似度NCC来衡量,定义如下:
(18)
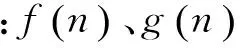
图2和图3分别所示为含不同宽度和幅值的大尺度方波和充放电三角波模拟信号经LMD分解后得到的各阶PF分量效果图。

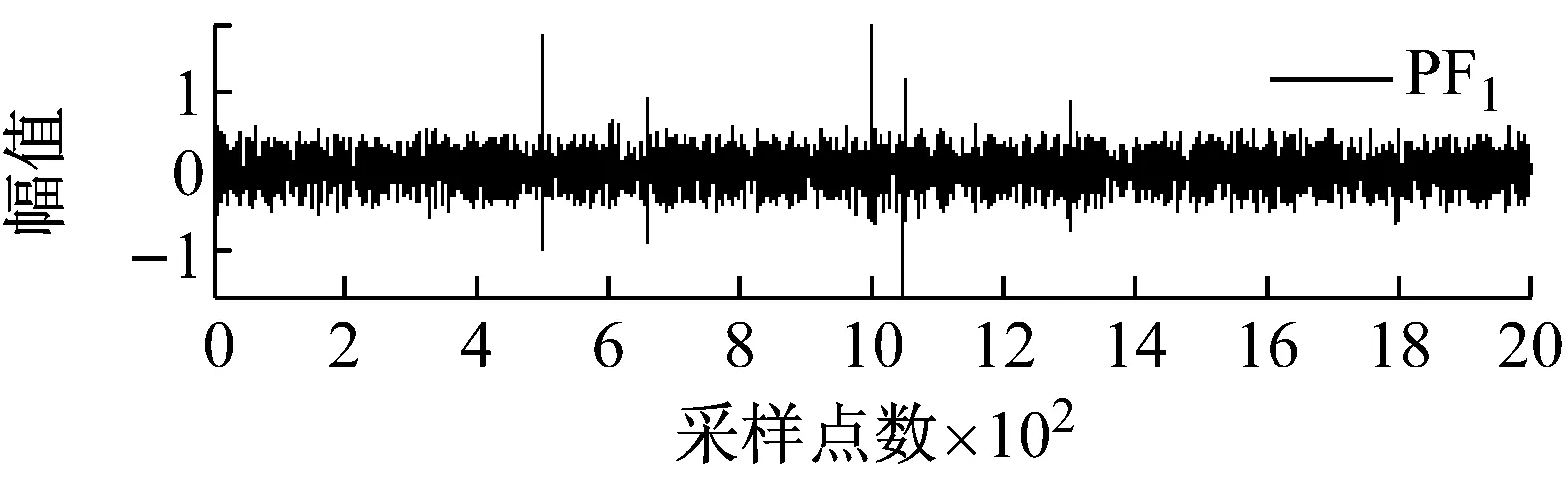
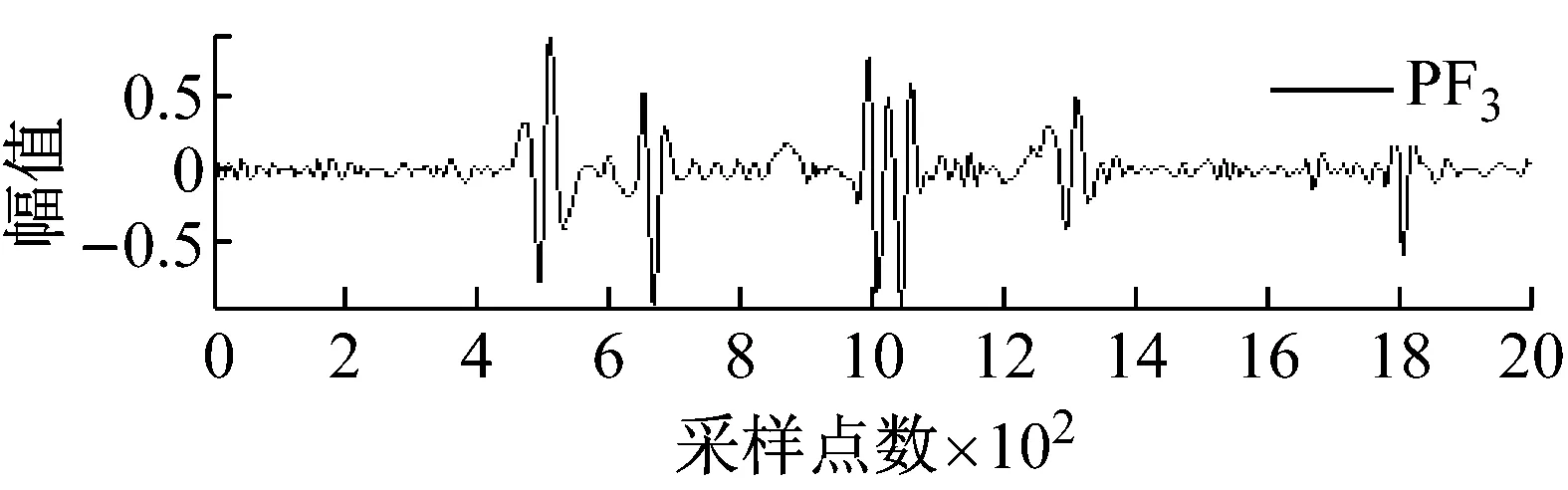
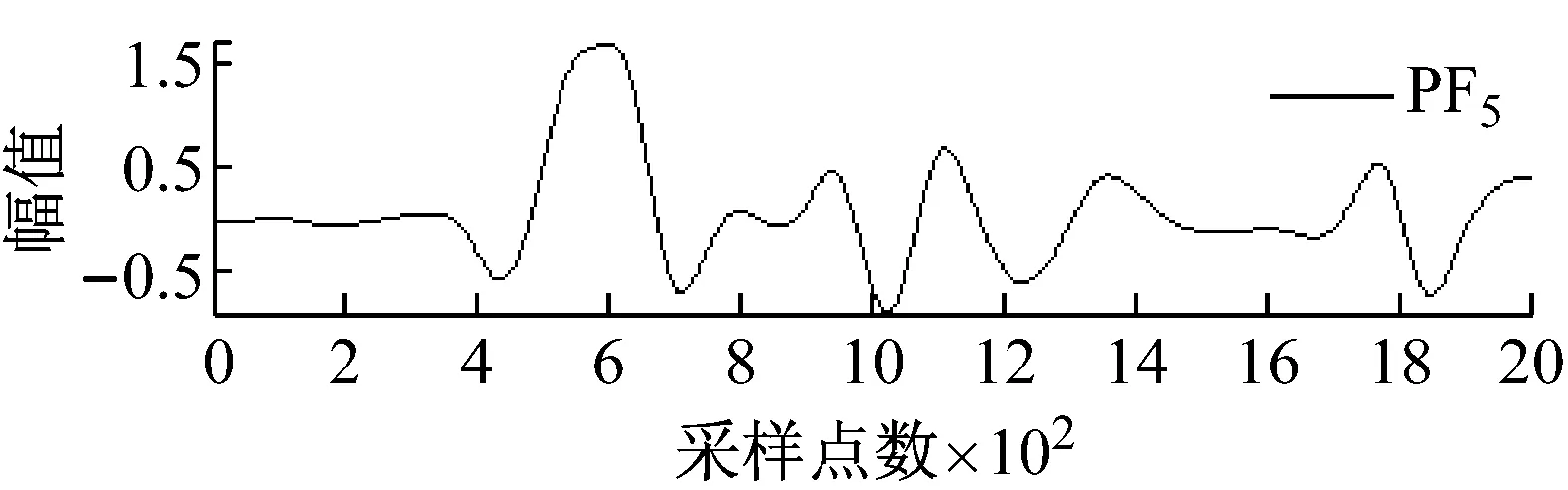
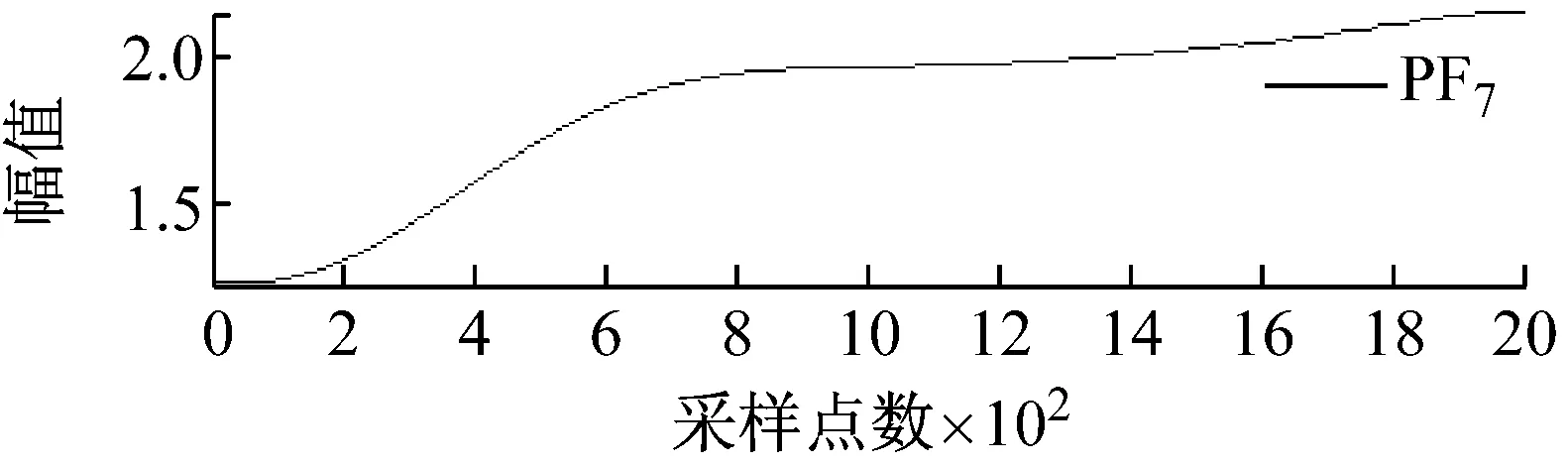
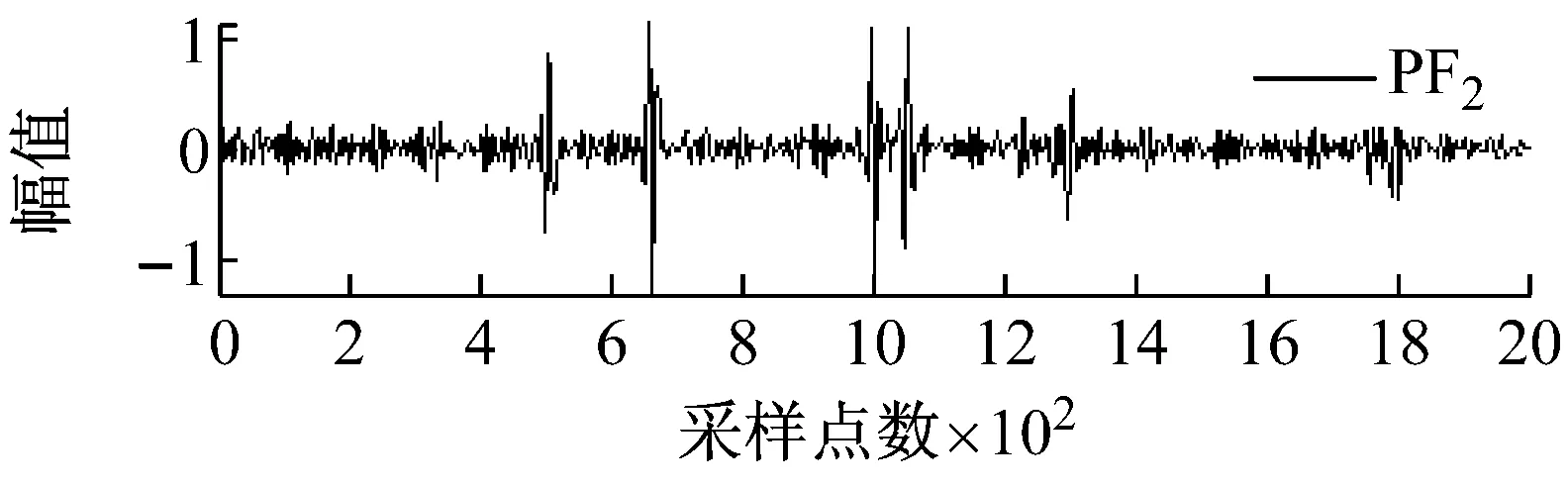
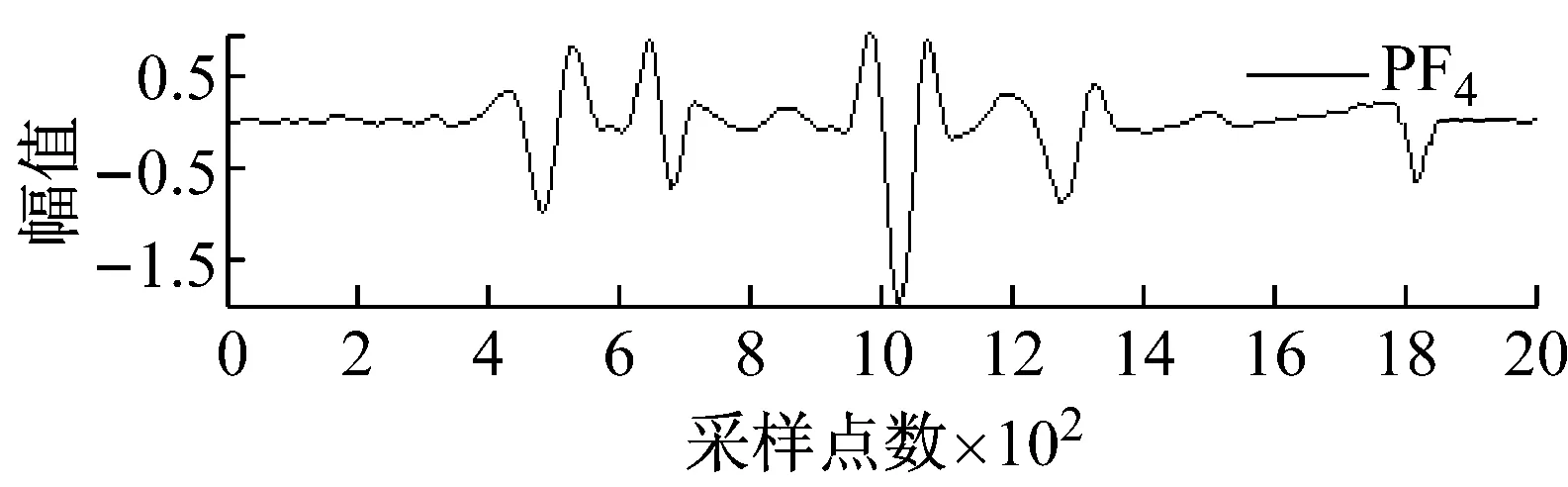
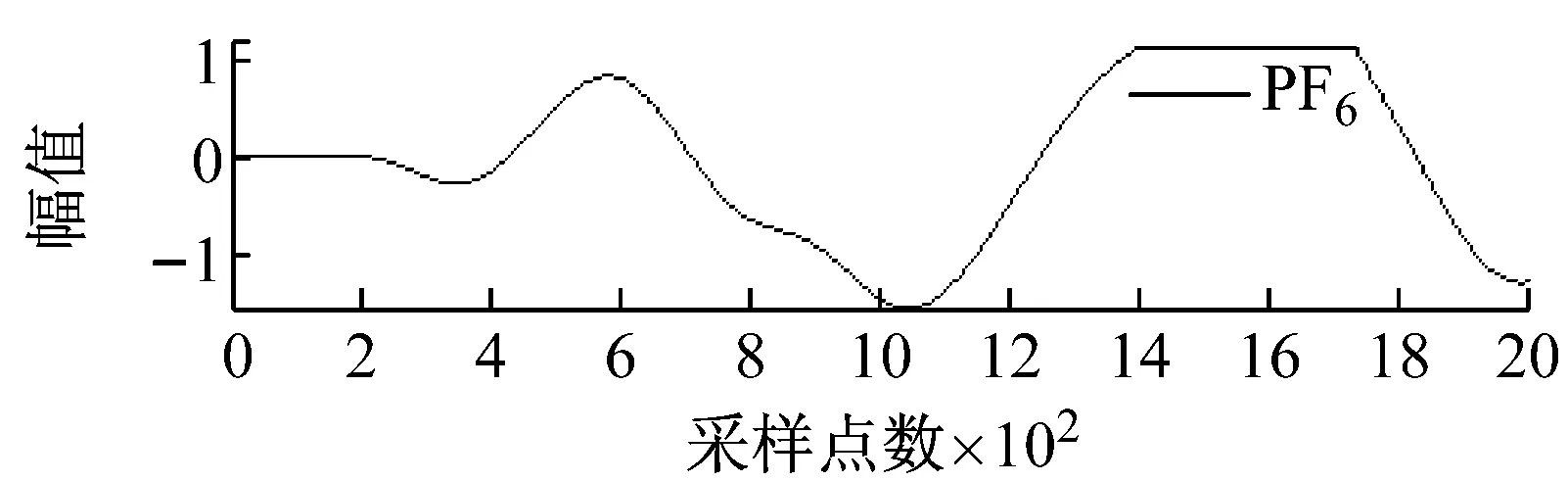
图2 大尺度方波模拟信号LMD分解图
Fig.2 LMD decomposition of large-scale square simulation signal

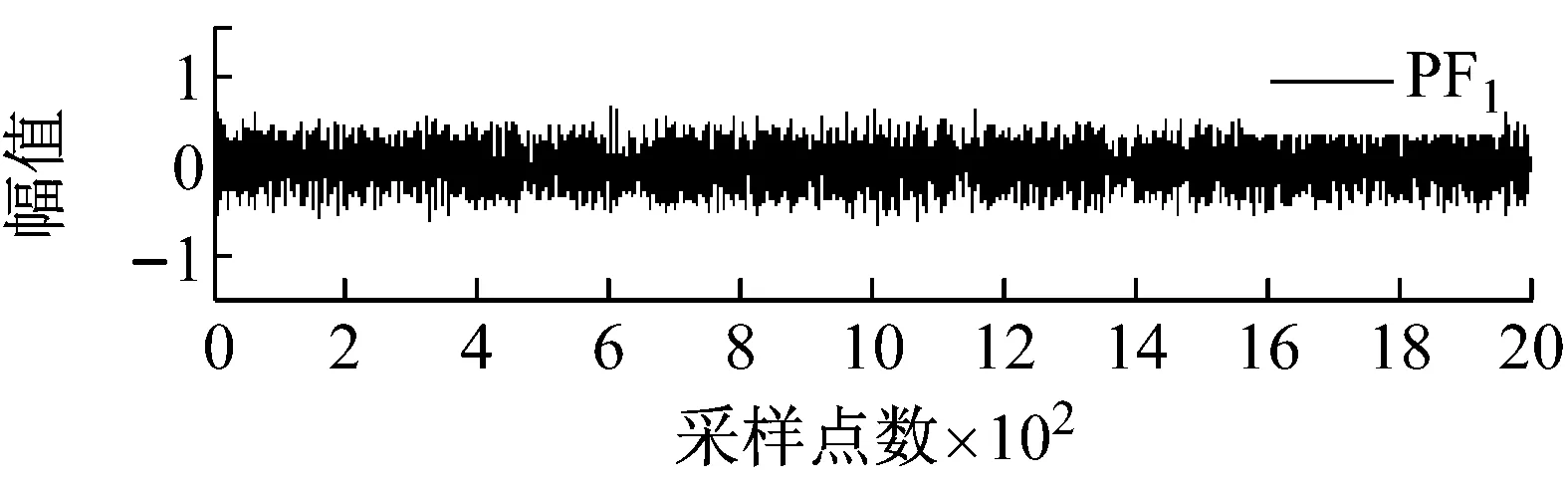
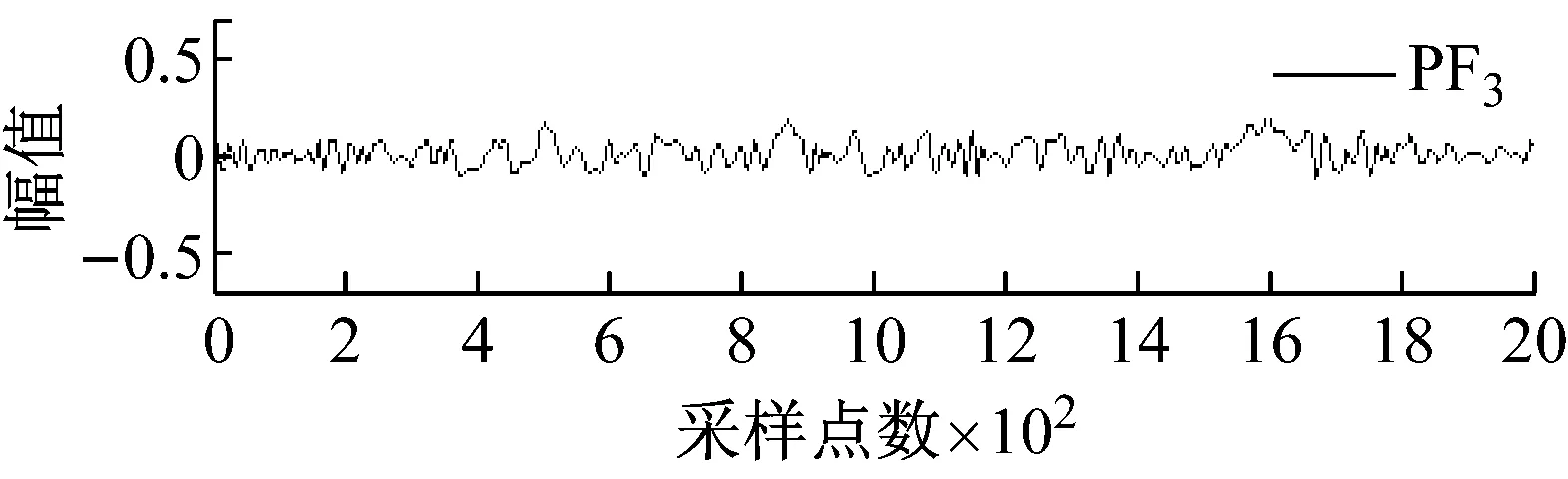

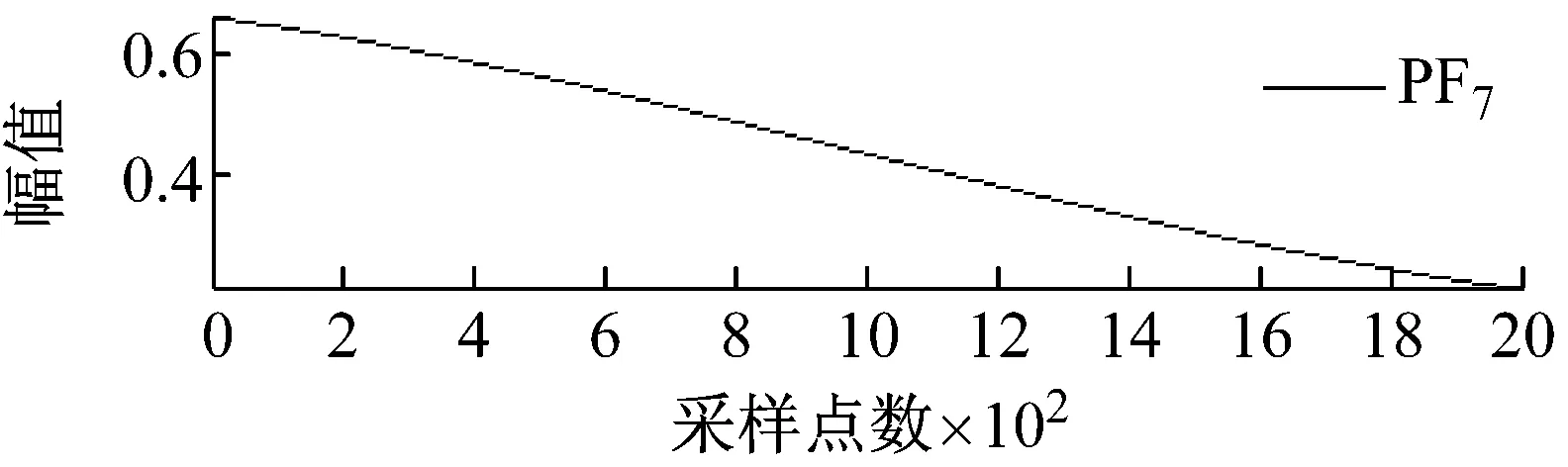

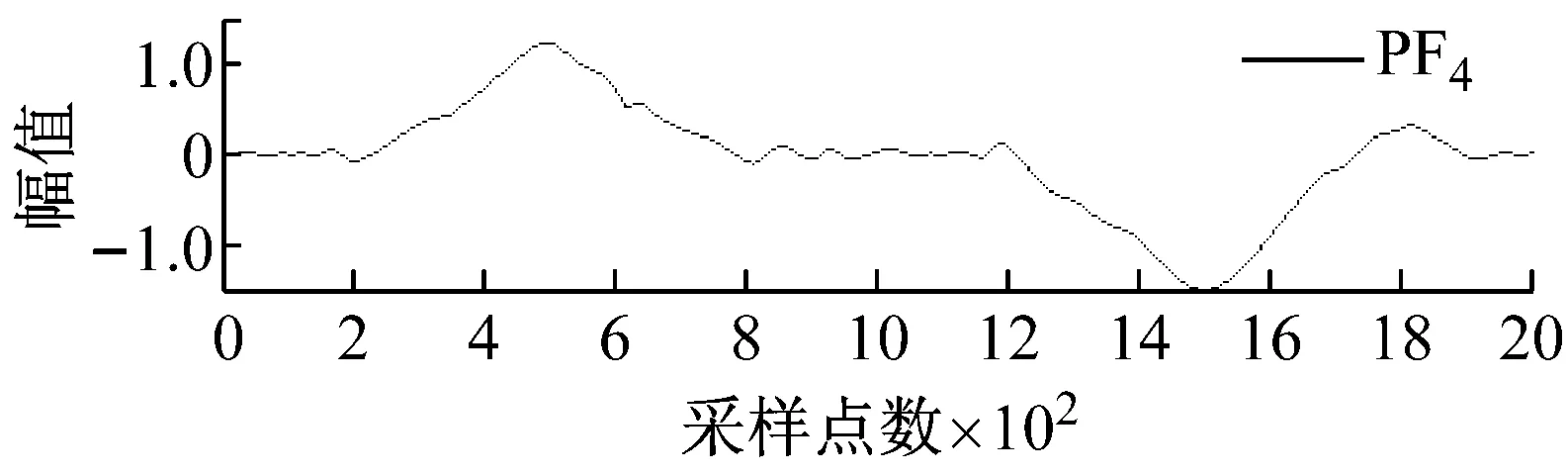

图3 大尺度充放电三角波模拟信号LMD分解图
Fig.3 LMD decomposition of large-scale charging and discharging triangular simulation signal
从图2和图3可知,局域均值分解将大尺度方波和充放电三角波模拟信号自适应地分解为7阶PF分量,每阶PF分量都与一定的物理过程相对应,将各阶PF分量的瞬时频率和瞬时幅值组合则可得到原始信号完整的时频分布。根据大地电磁信噪特征分析大尺度方波和充放电三角波模拟信号的LMD分解结果可以发现,分解得到的PF1分量通常由大量类似于大地电磁信号的随机信息构成。为此,基于局域均值分解和小波阈值的大地电磁噪声压制方法其具体步骤如下:首先,利用局域均值分解的自适应性将大地电磁信号分解为若干阶PF分量;然后,保留PF1分量,仅对其余各阶PF分量选择合适的阈值进行小波阈值去噪;最后,将处理后的小波系数叠加重构获得大地电磁有用信号。由于硬阈值函数在阈值处不连续,易导致重构信号出现伪吉布斯现象,因此文中均采用软阈值函数进行处理,目的是使其尽可能多地保留有用信号,减少重构信号与真实信号之间的偏差。
图4所示为大尺度方波和充放电三角波模拟信号采用本文所提方法的噪声压制效果图。
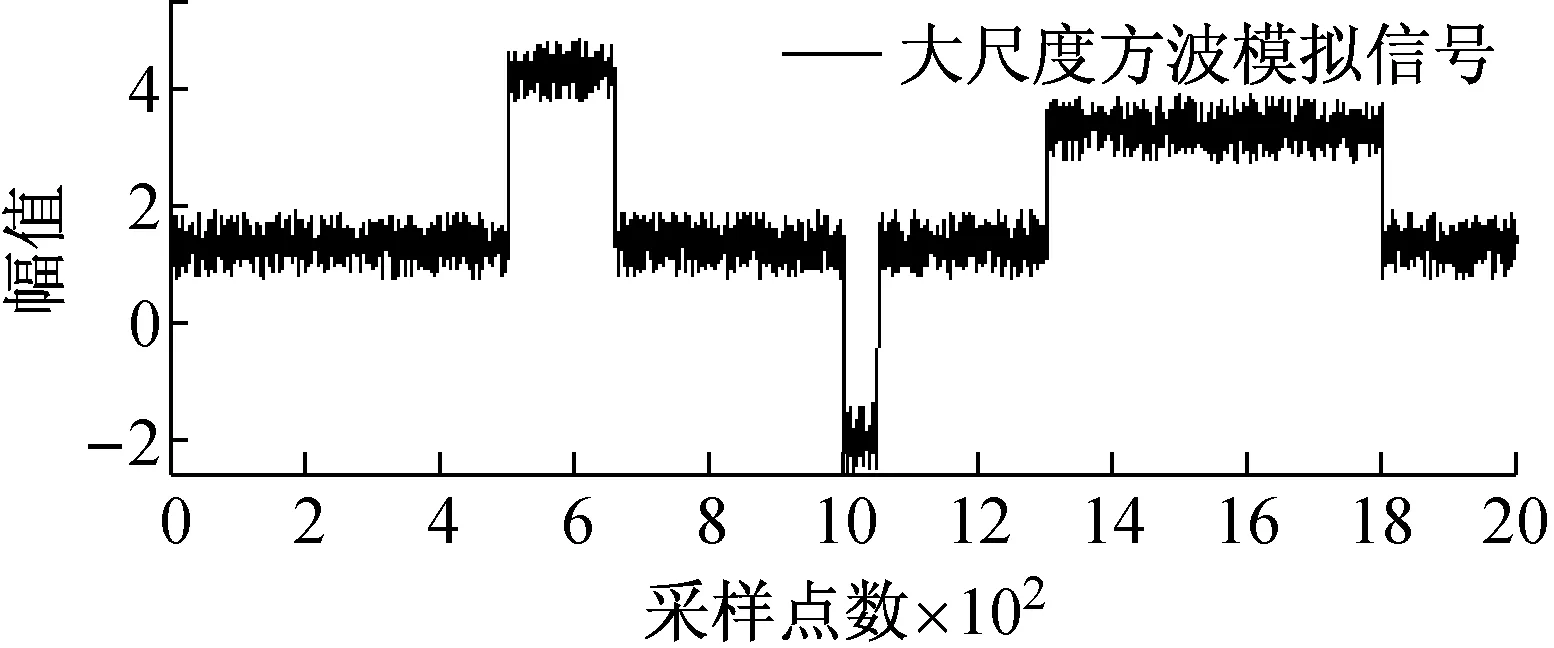
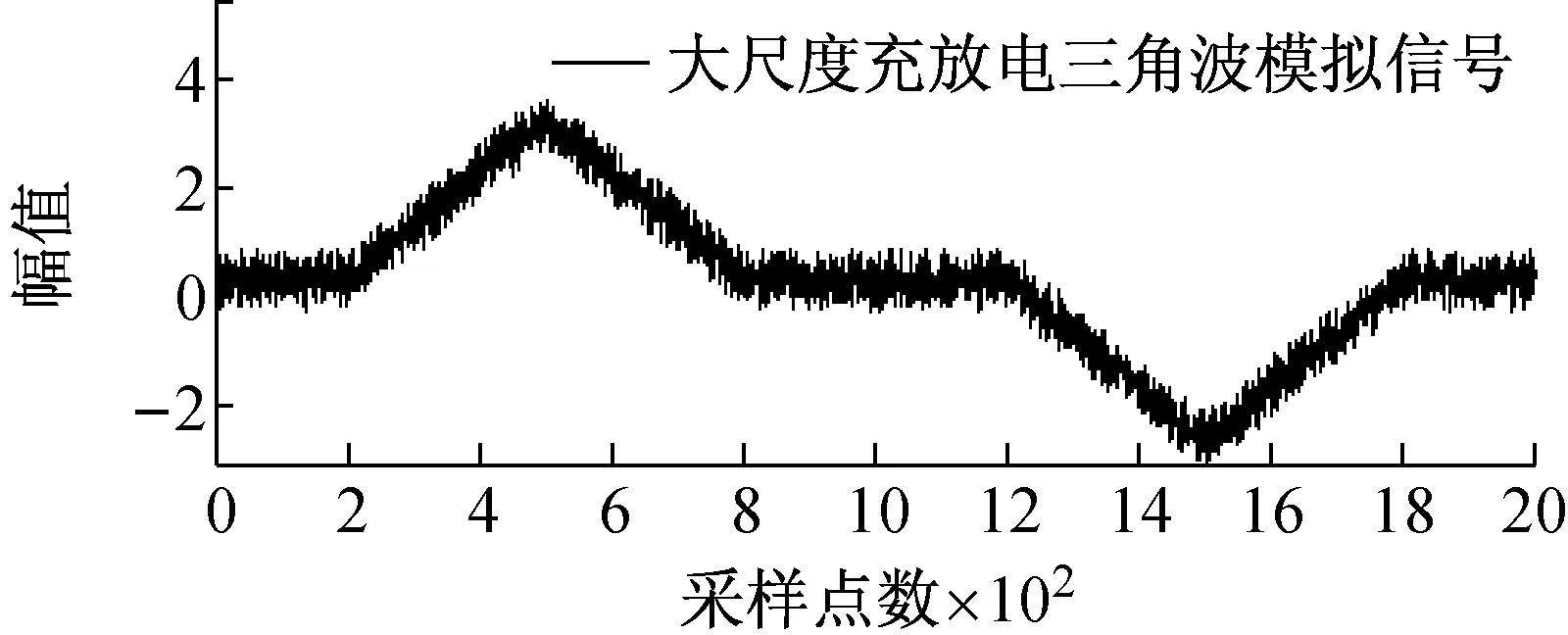

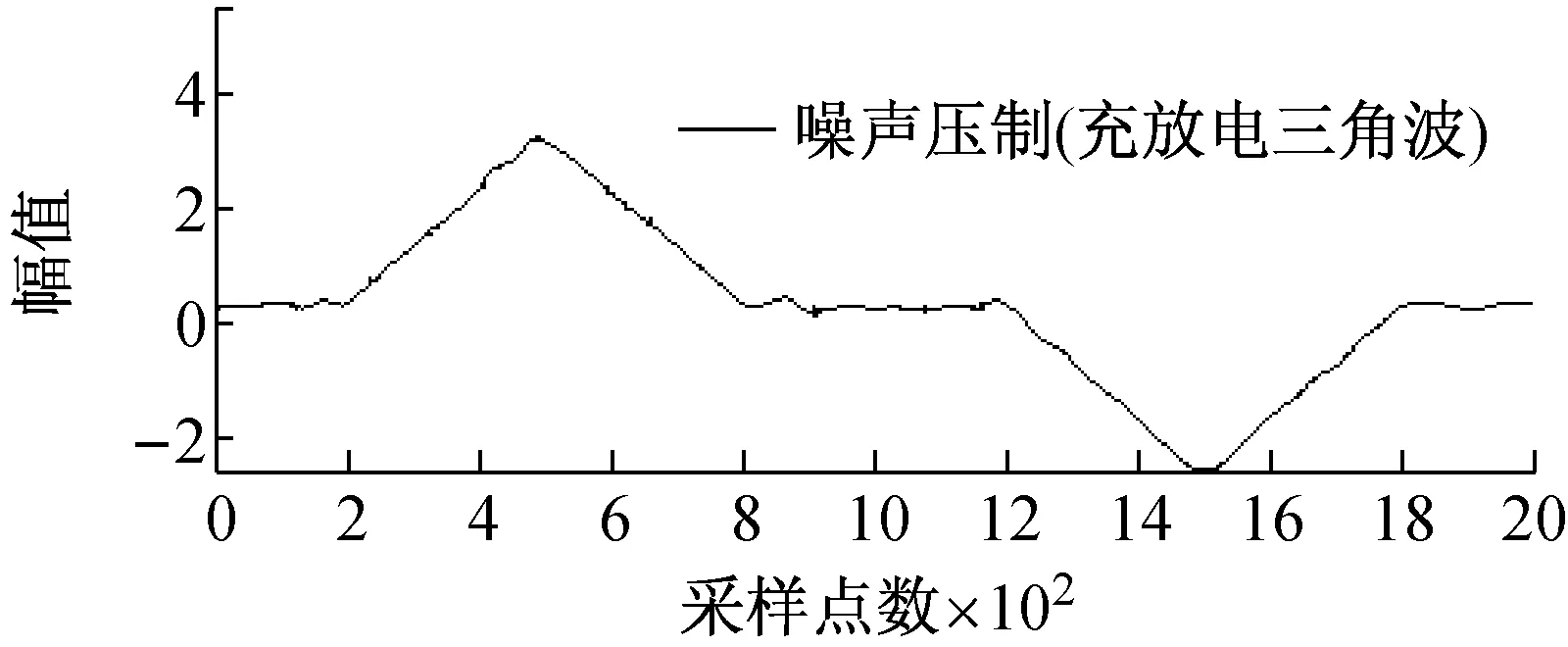

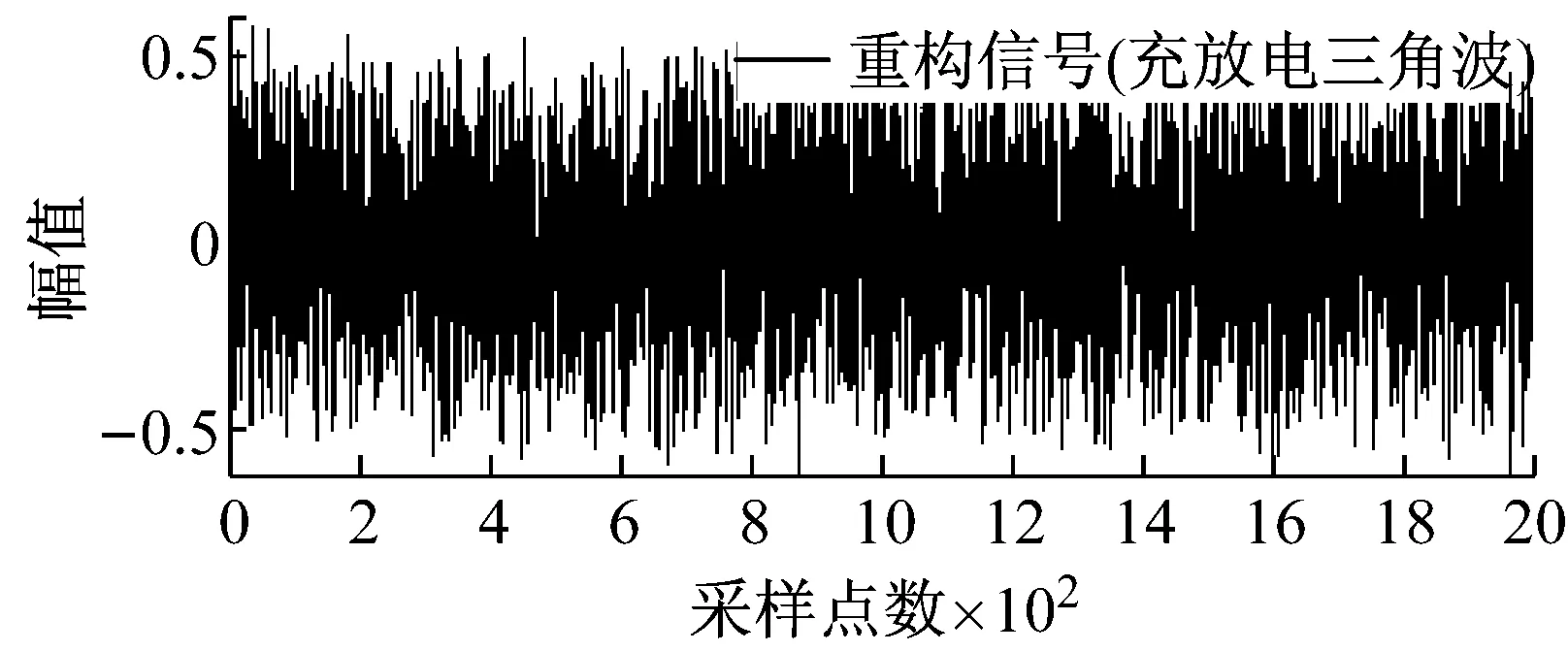
图4 大尺度模拟信号去噪效果图
Fig.4 Denoising effect of large-scale simulation signal
从图4可知,文中所提方法在压制大尺度方波和充放电三角波的同时,原始信号中丰富的细节成分得到了有效保留。
为进一步分析算法性能,表1所示为模拟信号经LMD分解后,再利用不同小波函数、分解层数及阈值方式获得的曲线相似度对比情况。
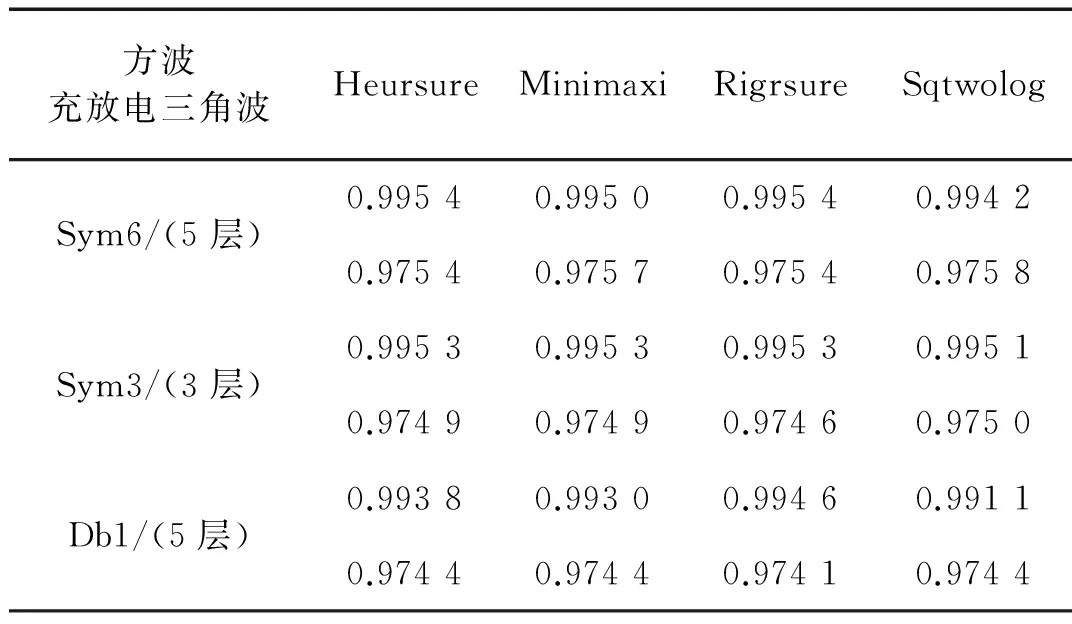
表1 曲线相似度对比Tab.1 The contrastion of curve similarity
分析表1可知,对于大尺度方波模拟信号在Heursure 和Rigrsure方式下采用sym6小波函数进行5层分解得到的曲线相似度最高(NCC=0.995 4);对于大尺度充放电三角波模拟信号在Sqtwolog方式下采用sym6小波函数进行5层分解得到的曲线相似度最高(NCC=0.975 8)。上述仿真实验为有针对性地选取滤波参数处理实测大地电磁强干扰类型提供了一定的依据。
4 实际资料处理
4.1 时间域去噪效果
为了验证本文方法的实用性,对矿集区采集到的受强干扰严重的大地电磁数据进行噪声压制。鉴于大地电磁数据量庞大且噪声类型复杂多样,文中给出一段某测点在同一时刻采集的含强干扰的电、磁场分量去噪效果图,如图5所示。
从图5可知,由于矿集区人烟稠密、重工业密集,导致电道和磁道中采集的大地电磁数据均不同程度地受到了类似于周期性突跳和波动等大尺度方波及充放电三角波干扰,且电道Ex/Ey和磁道Hy/Hx出现干扰的时刻具有一定的相关性,微弱的大地电磁有用信号几乎被完全湮没。经本文所提方法处理后,大尺度强干扰的轮廓特征被较好地提取,且曲线光滑、连续;重构的大地电磁信号则在剔除基线漂移的同时,保留了有用信号更多的细节信息,原始大地电磁信号的基本特征得到了较好的还原。
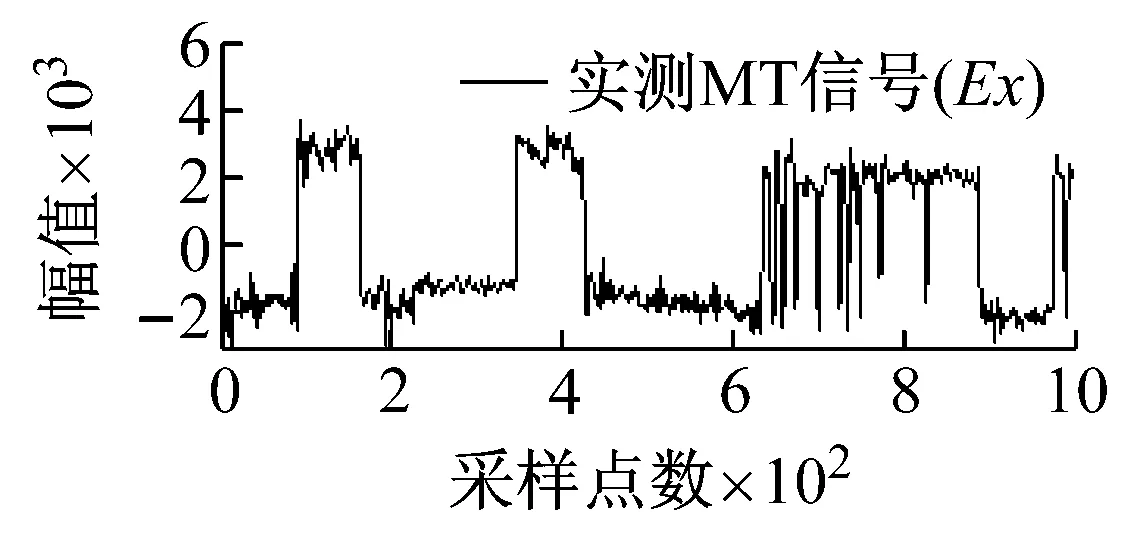
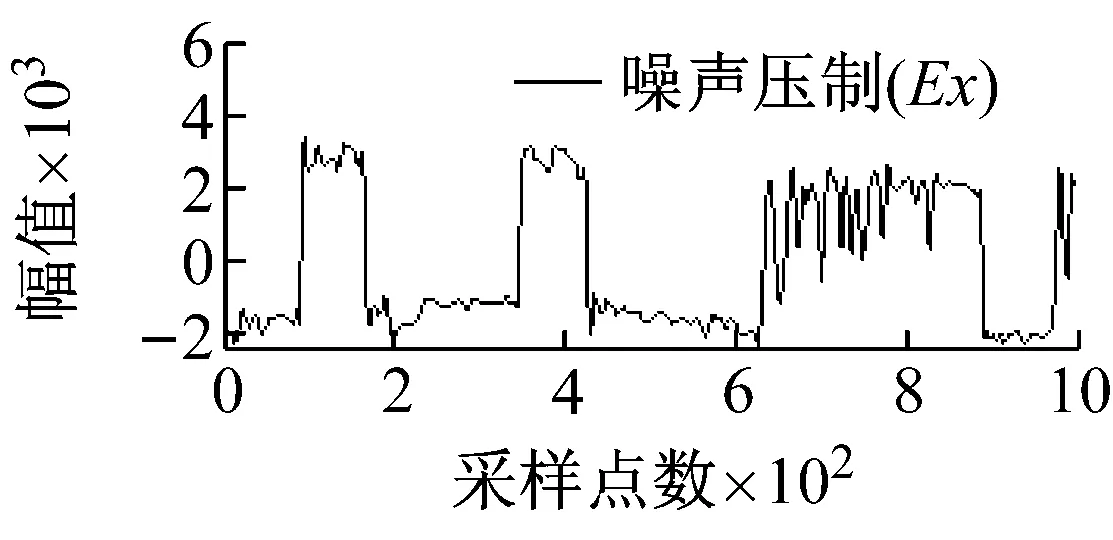
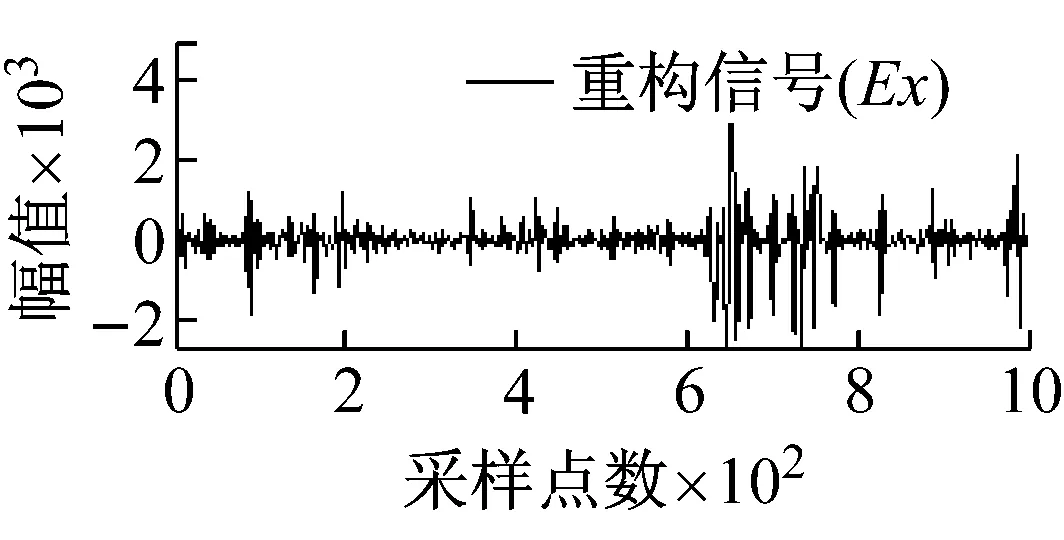
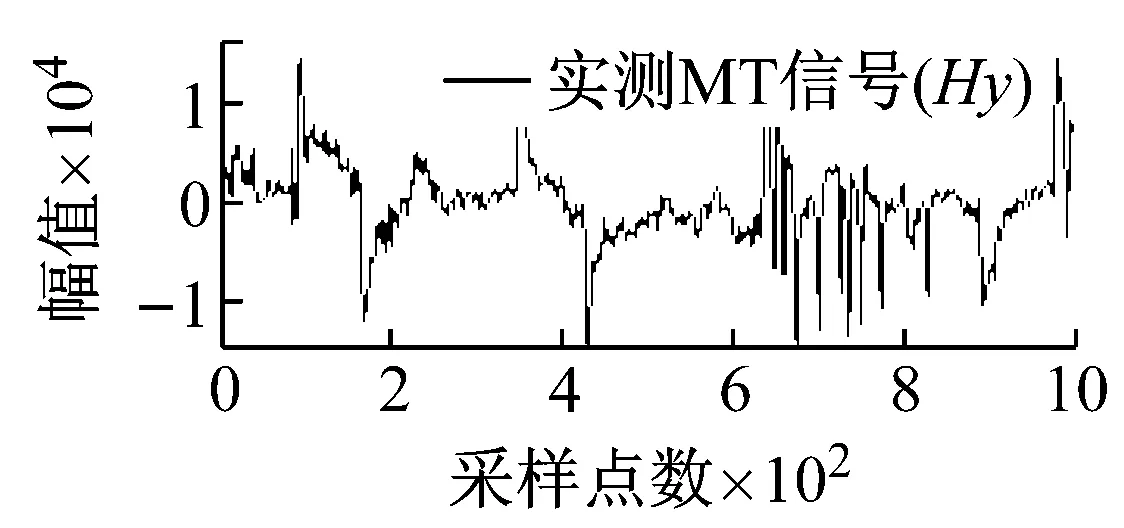
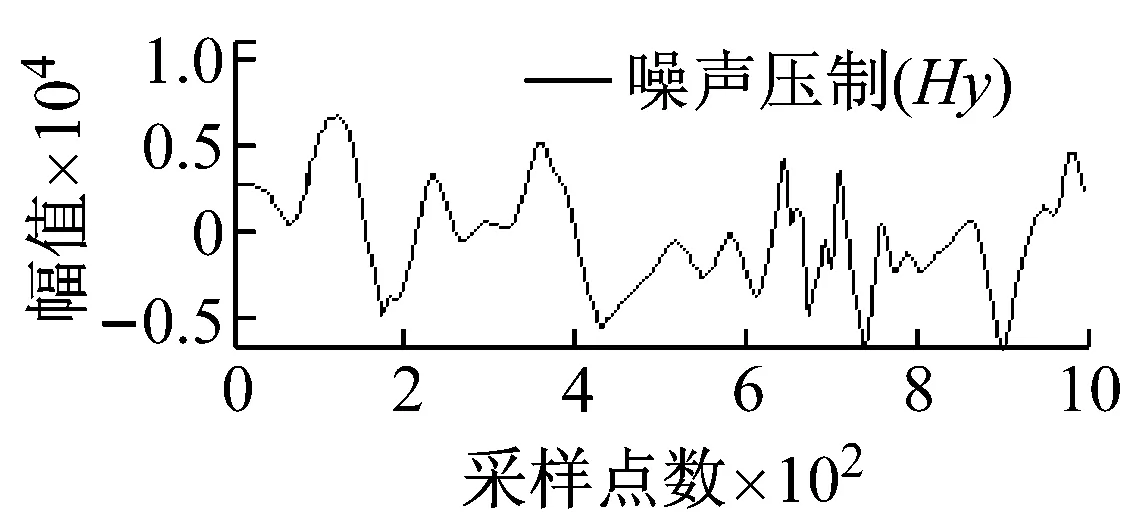
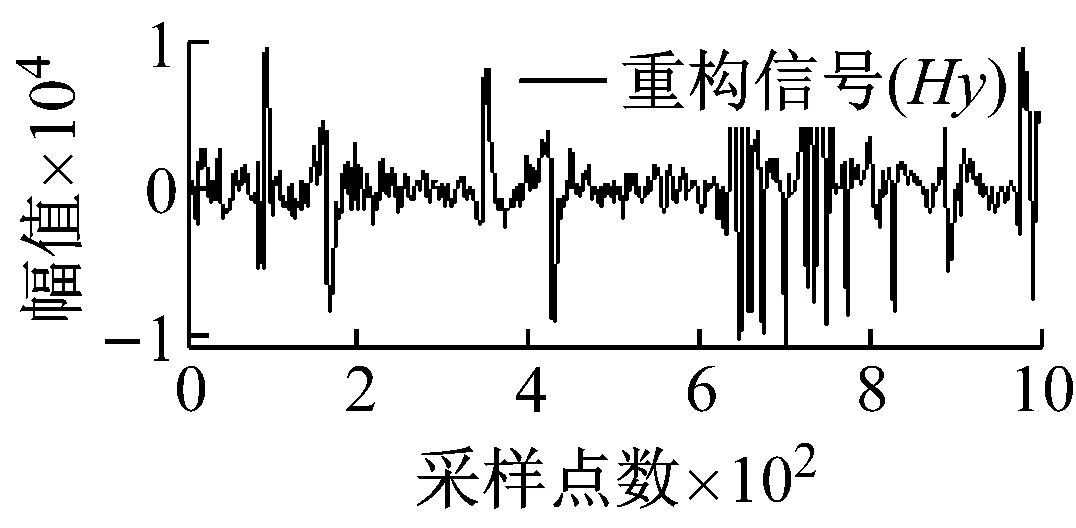
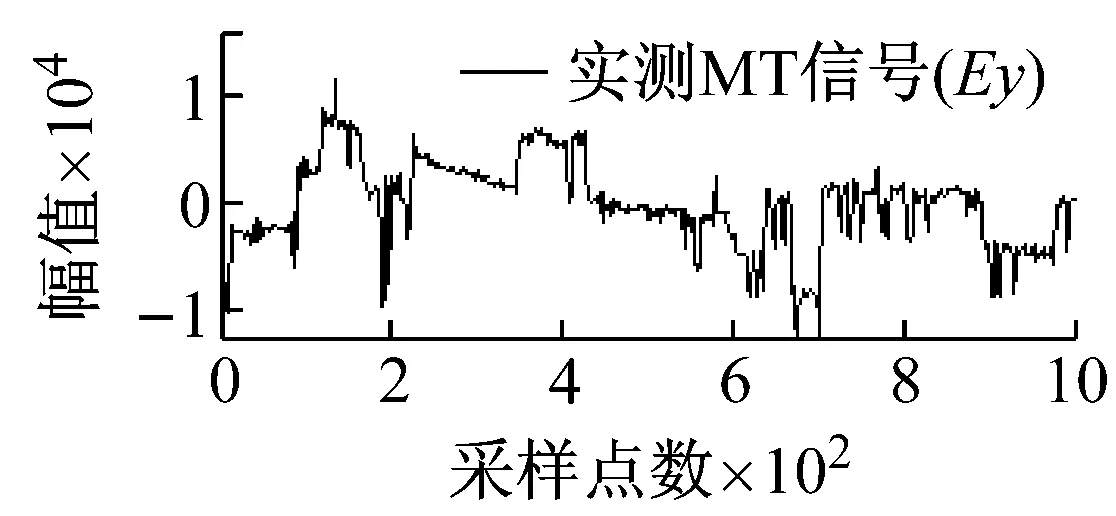
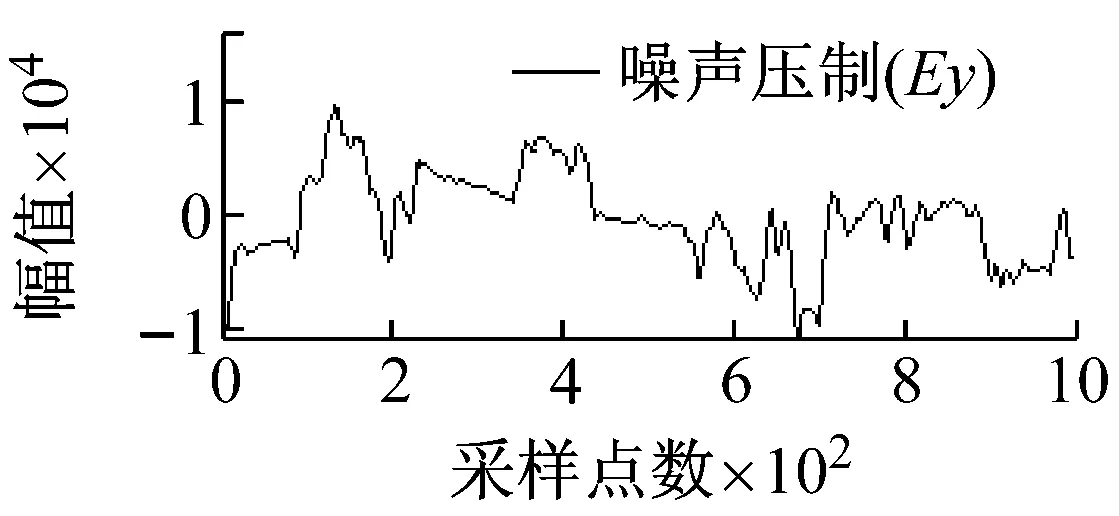
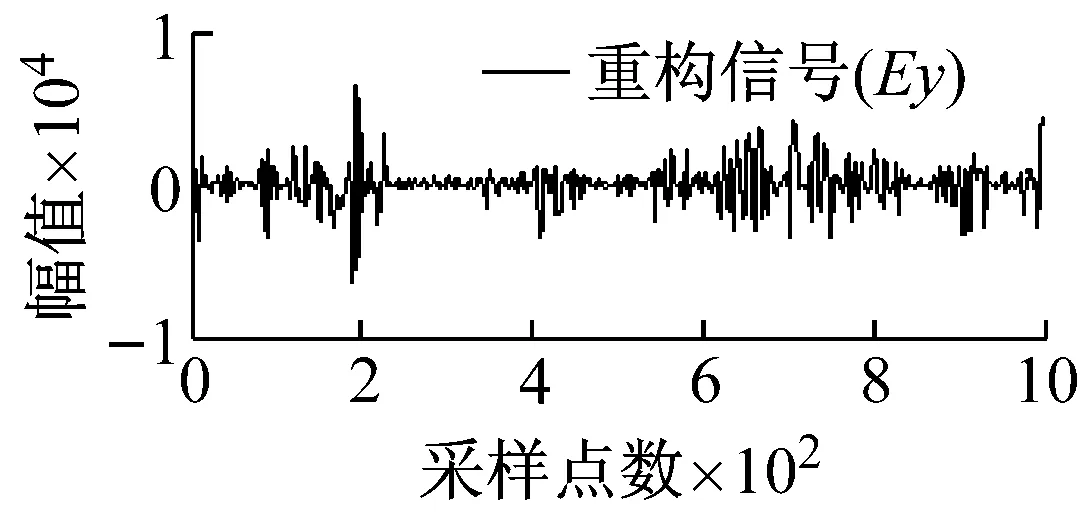
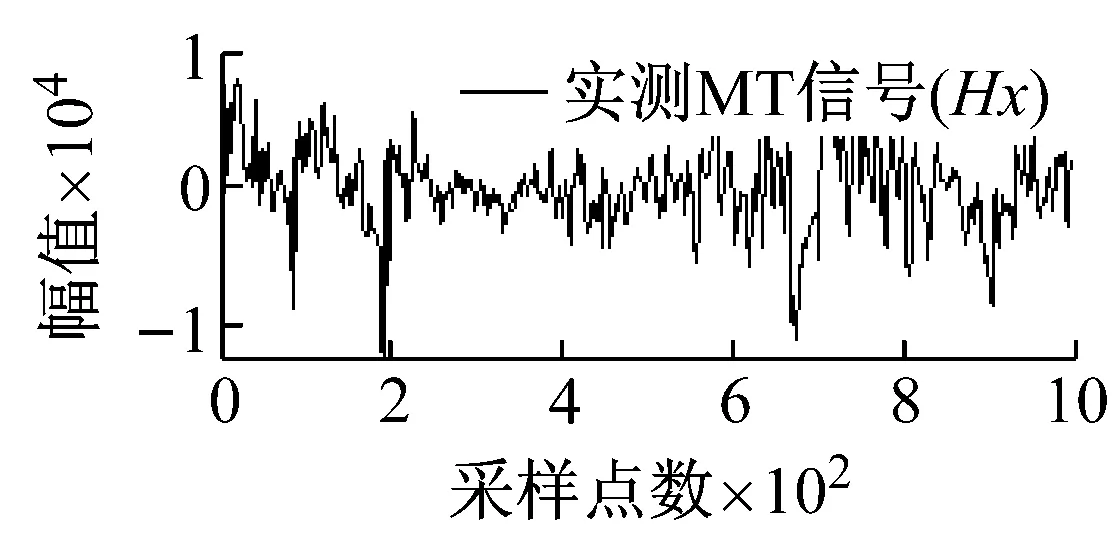
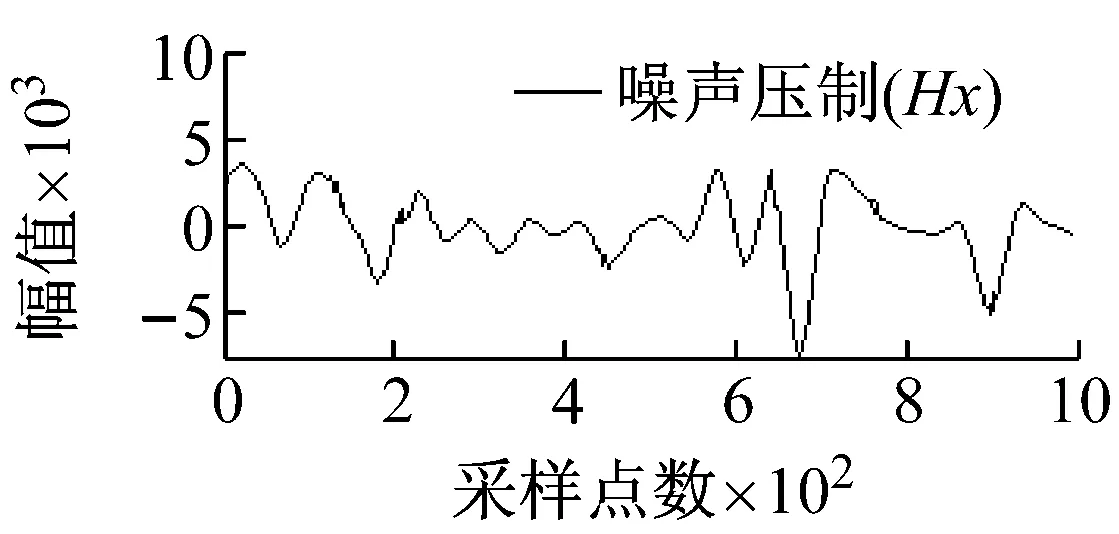
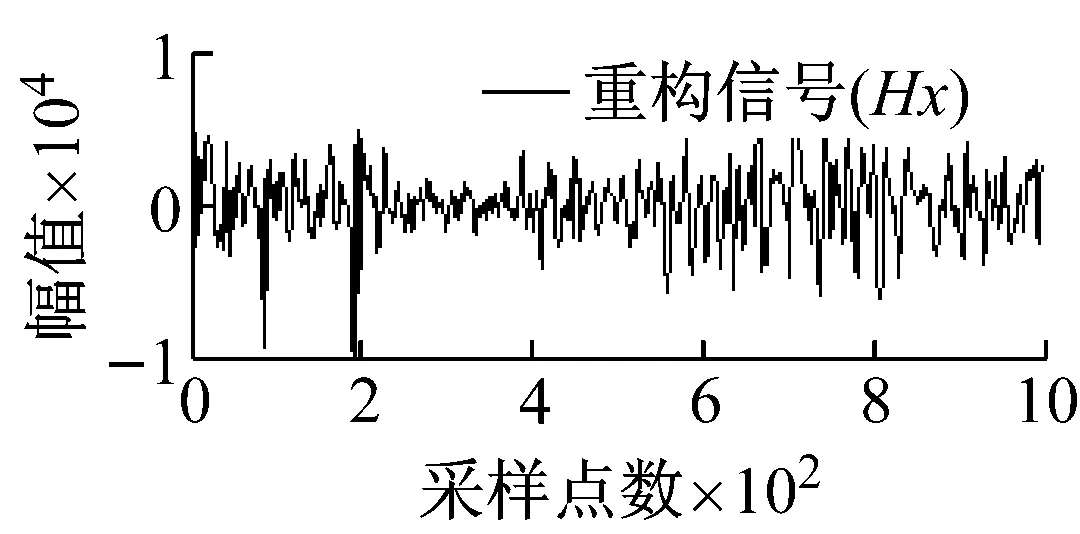
图5 实测MT信号去噪效果图
Fig.5 Denoising effect of measured MT signal
4.2 实测点处理效果
文中选用的实测大地电磁数据由加拿大凤凰公司生产的V5-2000大地电磁测深仪采集,该仪器的数据采集方式是1-8-5模式。以TSL、TSH文件为例,低频段的数据为全时间段采集(采样率为24 Hz),数据存储为TSL文件;高频和中频是交替采集,每5 min采集1次高频或中频,其中有1 s的高频数据(采样率2 560 Hz)和连续8 s的中频数据(采样率为320 Hz),采样起止时间相同,数据存储为TSH文件。因此,大部分反映测点信息的数据集中在低频段,对矿集区大地电磁数据进行噪声压制主要是针对低频段的典型强干扰异常波形进行处理。为此,文中重点对TSL文件中的大地电磁数据进行降噪处理。分析V5-2000数据存储格式可知,参与计算的视电阻率值其频率成分最多至0.8 Hz左右。
图6和图7分别所示为庐枞矿集区实测点B40492和B44249原始数据和本文所提方法在时间域波形及视电阻率曲线两方面的去噪效果对比图。两测点数据采集时间均在20 h以上,其中时间域波形的观测环境为V5 System 2000。
分析图6(a)和图7(a)可知,由于两测点面临复杂的噪声干扰环境,原始数据的电道(Ex、Ey)和磁道(Hx、Hy)中均出现大尺度方波和充放电三角波干扰,且能量幅值远大于大地电磁有用信号几个数量级,正常的大地电磁信号几乎被完全湮没。图6(b)和图7(b)为经文中方法处理后,将大地电磁数据重新还原至V5 System 2000观测的时间域波形。对比分析图6(a)和图7(a)可知,大尺度方波和充放电三角波干扰均得到了有效剔除,微弱的大地电磁有用信号基本集中在基线附近且无明显跳变。
观测实测点B40492原始数据的视电阻率曲线(图6(c))可知,大约在50~0.05 Hz频段视电阻率曲线呈近45°渐近线快速上升,且曲线光滑、几乎没有误差棒,该频段内近13个频点的数据完全失真;在0.05 Hz左右,视电阻率值达到最大,接近于1 000 000 Ω·m;0.05~0.005 Hz频段的视电阻率值突然下降至1 000 Ω·m左右,视电阻率曲线的误差棒增大,且曲线跳变剧烈,该现象属于典型的近源效应。因此,由原始测点数据得到的视电阻率曲线俨然已不能客观反映测点本身所固有的地下介质电性结构。分析图6(d)可知,经本文所提方法处理后,0.8~0.05 Hz频段的视电阻率曲线近45°上升的近源效应有明显缓解,视电阻率最大值下降了近2个数量级,该频段内挽救了近9个频点的数据;0.05~0.000 5 Hz超低频段,视电阻率曲线更为光滑、连续,视电阻率值相对稳定,且误差棒减小。分析实测点B44249原始数据的视电阻率曲线(图7(c))可知,曲线形态同样具有典型的近源效应,且在低频段曲线震荡剧烈、误差棒增大。经文中所提方法(图7(d))处理后,视电阻率曲线近45°上升的近源效应得到了有效压制,视电阻率曲线形态更为光滑、连续,误差棒减小、视电阻率值相对稳定,低频段的大地电磁数据质量得到了明显改善。




(a) 原始数据时间域波形




(b) 本文所提方法时间域波形
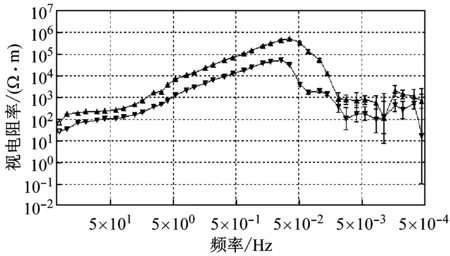
(c) 原始数据视电阻率曲线
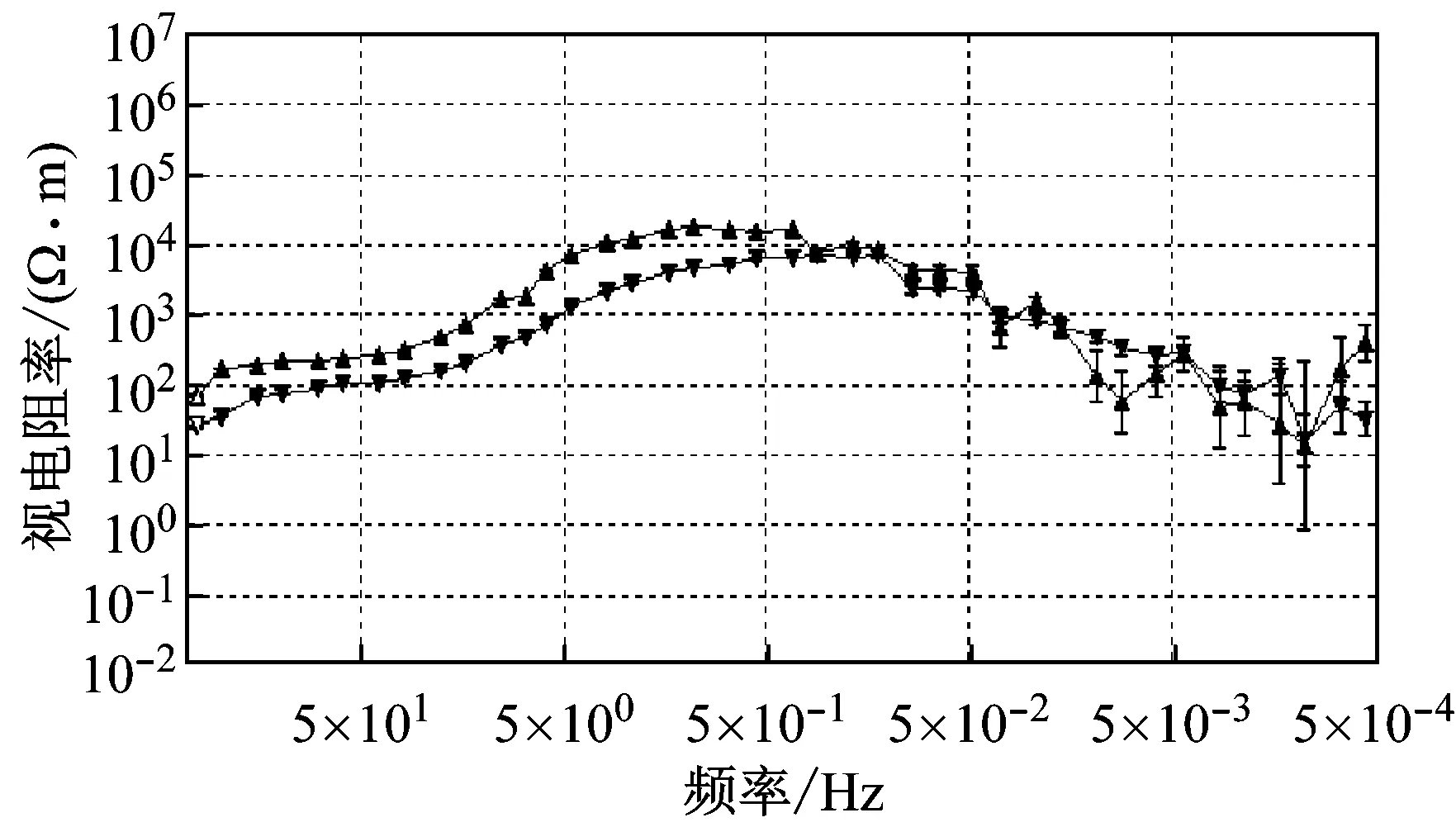
(d) 本文所提方法视电阻率曲线




(a) 原始数据时间域波形




(b) 本文所提方法时间域波形
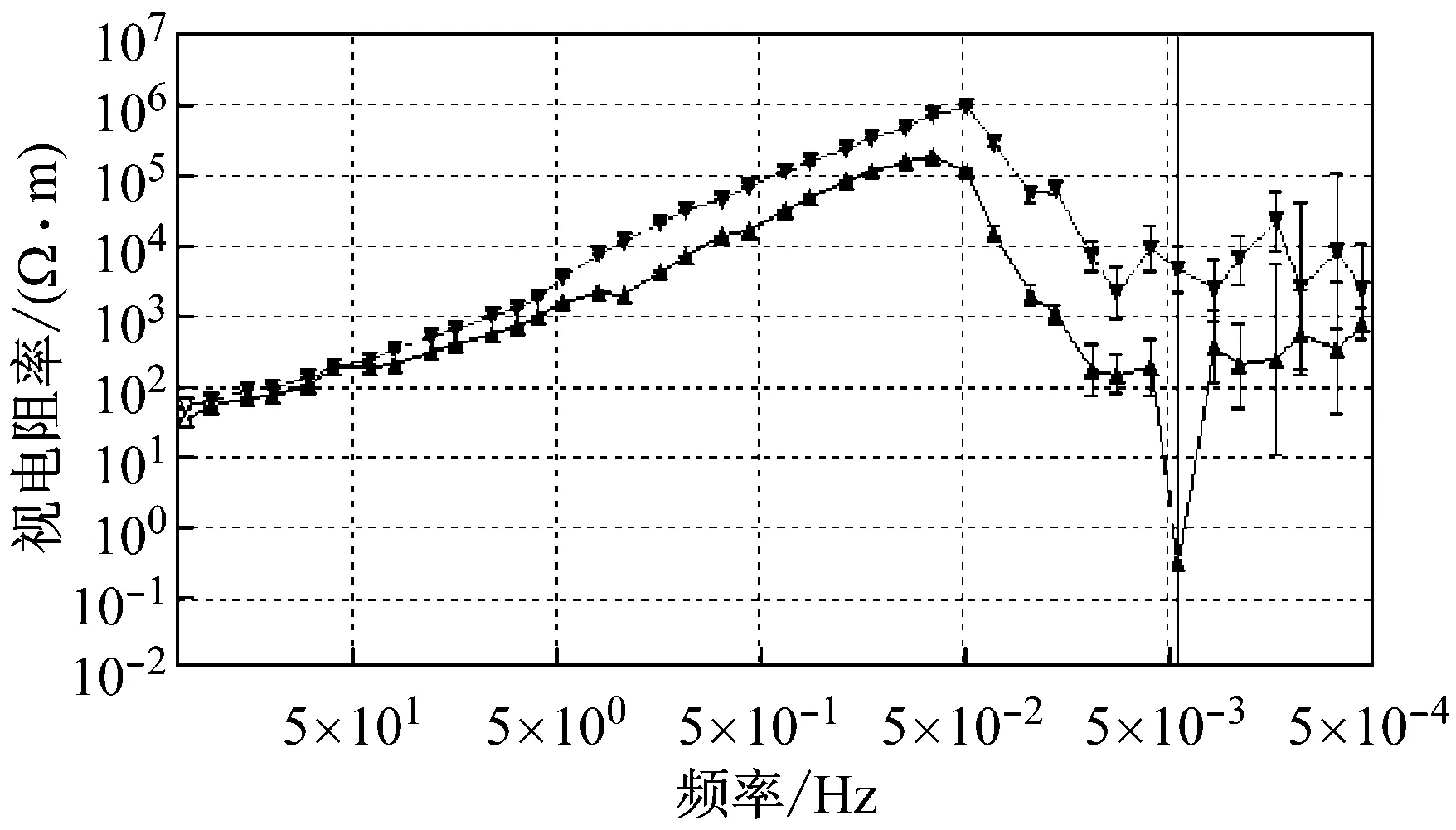
(c) 原始数据视电阻率曲线
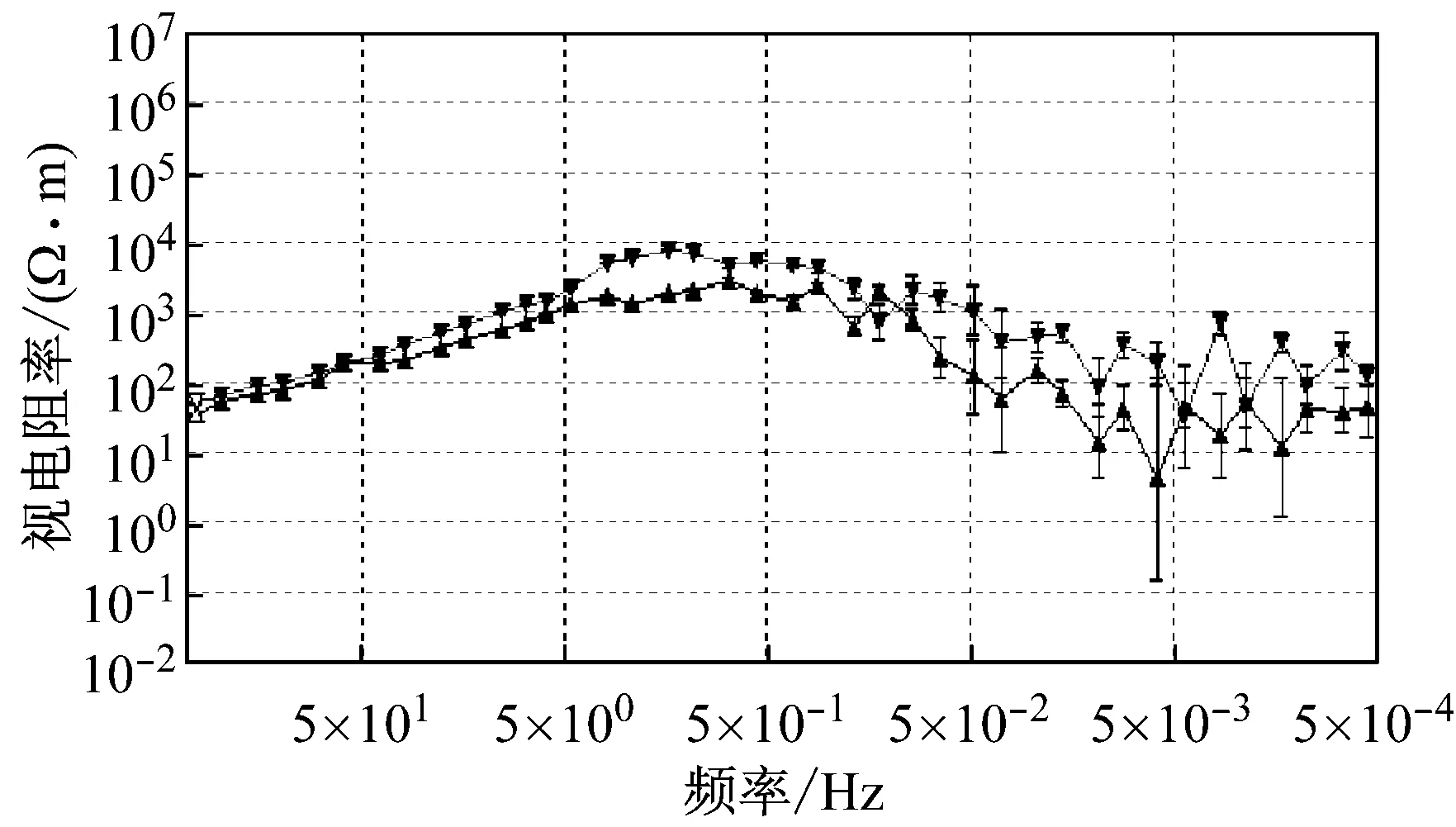
(d) 本文所提方法视电阻率曲线
5 结 论
(1) 提出了一种基于局域均值分解和小波阈值的大地电磁噪声压制方法。将局域均值分解的自适应性和小波分析的多分辨性相结合,应用于矿集区大地电磁微弱信号和大尺度强干扰的信噪分离,达到了噪声压制目的,大尺度异常波形和基线漂移均得到了有效压制。
(2) 通过模拟信号仿真分析和实测资料数据处理,证明了方法的实用性。受近源干扰严重的测点经文中所提方法处理后,视电阻率曲线的整体形态更为光滑、连续,近源干扰得到了有效压制,其结果更加真实地反映了测点本身所固有的大地电磁深部构造信息。方法为今后在矿集区开展大地电磁测深提供了一条新的解决途径,应用前景广阔。
[1] CHEN J, HEINCKE B, JEGEN M, et al.Using empirical mode decomposition to process marine magnetotelluric data[J].Geophysical Journal International, 2012, 190(1): 293-309.
[2] 汤井田, 徐志敏, 肖晓, 等.庐枞矿集区大地电磁测深强噪声的影响规律[J].地球物理学报, 2012, 55(12): 4147-4159.
TANG Jingtian, XU Zhimin, XIAO Xiao, et al.Effect rules of strong noise on magnetotelluric (MT) sounding in the Luzong ore cluster area[J].Chinese J.Geophys., 2012, 55(12): 4147-4159.
[3] CAI J H, TANG J T, HUA X R, et al.An analysis method for magnetotelluric data based on the Hilbert-Huang transform[J].Exploration Geophysics, 2009, 40(2): 197-205.
[4] 景建恩, 魏文博, 陈海燕, 等.基于广义S变换的大地电磁测深数据处理[J].地球物理学报, 2012, 55 (12): 4015-4022.
JING Jianen, WEI Wenbo, CHEN Haiyan, et al.Magnetotelluric sounding data processing based on generalized S transformation[J].Chinese J.Geophys., 2012, 55(12): 4015-4022.
[5] KAPPLE K N.A data variance technique for automated despiking of magnetotelluric data with a remote reference[J].Geophysical Prospecting, 2012, 60(1): 179-191.
[6] 王辉, 魏文博, 金胜, 等.基于同步大地电磁时间序列依赖关系的噪声处理[J].地球物理学报, 2014, 57(2): 531-545.
WANG Hui, WEI Weibo, JIN Sheng, et al.Removal of magnetotelluric noise based on synchronous time series relationship[J].Chinese J.Geophys., 2014, 57(2): 531-545.
[7] 汤井田, 李晋, 肖晓, 等.数学形态滤波与大地电磁噪声压制[J].地球物理学报, 2012,55(5): 1784-1793.
TANG Jingtian, LI Jin, XIAO Xiao, et al.Mathematical morphology filtering an noise suppression of magnetotelluric sounding data[J].Chinese J.Geophys., 2012, 55(5): 1784-1793.
[8] 李晋, 汤井田, 王玲, 等.基于信号子空间增强和端点检测的大地电磁噪声压制[J].物理学报, 2014, 63(1): 019101.
LI Jin, TANG Jingtian, WANG Ling, et al.Noise suppression for magnetotelluric sounding data based on signal subspace enhancement and endpoint detection[J].Acta Phys.Sin., 2014, 63(1): 019101.
[9] 程军圣, 杨宇, 于德介.局部均值分解方法及其在齿轮故障诊断中的应用[J].振动工程学报, 2009, 22(1): 76-84.
CHENG Junsheng, YANG Yu, YU Dejie.The local mean decomposition method and its application to gear fault diagnosis[J].Journal of Vibration Engineering, 2009, 22(1): 76-84.
[10] 李志农, 刘卫兵, 易小兵.基于局域均值分解的机械故障欠定盲源分离方法研究[J].机械工程学报, 2011, 47(7): 97-102.
LI Zhinong, LIU Weibing, YI Xiaobing.Underdetermined blind source separation method of machine faults based on local mean decomposition[J].Journal of Mechanical Engineering, 2011, 47(7): 97-102.
[11] 武哲, 杨绍普, 张建超.基于LMD自适应多尺度形态学和Teager能量算子方法在轴承故障诊断中的应用[J].振动与冲击, 2016, 35(3): 7-13.
WU Zhe, YANG Shaopu, ZHANG Jianchao.Bearing fault feature extraction method based on LMD adaptive multiscale morphology and energy operator demodulating[J].Journal of Vibration and Shock, 2016, 35(3): 7-13.
[12] 张焱, 汤宝平, 邓蕾, 等.基于局域均值分解的自适应滤波滚动轴承故障特征提取[J].振动与冲击, 2015, 34(23): 25-30.
ZHANG Yan, TANG Baoping, DENG Lei, et al.Fault feature extraction for rolling bearing based on adaptive wavelet filtering and LMD[J].Journal of Vibration and Shock, 2015, 34(23): 25-30.
[13] SMITH J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface, 2005, 2(5): 443-454.
[14] 侯高燕, 吕勇, 肖涵, 等.基于LMD的多尺度形态学在齿轮故障诊断中的应用[J].振动与冲击, 2014, 33(19): 69-73.
HOU Gaoyan, LÜ Yong, XIAO Han, et al.Based on the LMD and multi-scale morphology used in gear fault diagnosis[J].Journal of Vibration and Shock, 2014, 33(19): 69-73.
[15] 张亢, 程军圣, 杨宇.基于局部均值分解与形态谱的旋转机械故障诊断方法[J].振动与冲击, 2013, 32(9): 135-140.
ZHANG Kang, CHENG Junsheng, YANG Yu.Rotating machinery fault diagnosis based on local mean decomposition and pattern spectrum[J].Journal of Vibration and Shock, 2013, 32(9): 135-140.
[16] 汤井田, 张弛, 肖晓, 等.大地电磁阻抗估计方法对比[J].中国有色金属学报, 2013, 23(9): 2351-2358.
TANG Jingtian, ZHANG Chi, XIAO Xiao, et al.Comparison of methods for magnetotelluric impedance estimation[J].The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2351-2358.
[17] 李晋, 汤井田, 肖晓, 等.基于组合广义形态滤波的大地电磁资料处理[J].中南大学学报(自然科学版), 2014, 45(1): 173-185.
LI Jin, TANG Jingtian, XIAO Xiao, et al.Magnetotelluric data processing based on combined generalized morphological filter[J].Journal of Central South University (Science and Technology), 2014, 45(1): 173-185.
Application of local mean decomposition and wavelet threshold in magnetotelluric noise suppression
LI Jin1,2, PENG Chong1, TANG Jingtian2, YAN Huan1, CAI Jianhua3
(1.Institute of Physics and Information Science, Hunan Normal University, Changsha 410081, China;2.School of Geosciences and Info-Physics, Key Laboratory of Metallogenic Prediction of Non-Ferrous Metals and Geological Environment Monitor, Ministry of Education, Central South University, Changsha 410083, China;3.Department of Physics and Electronics, Hunan University of Arts and Science, Changde 415000, China)
The magnetotelluric sounding method is a method based on the principle of electromagnetic induction, to detect electrical properties and distribution characteristics of underground rock layers by use of the natural alternating electromagnetic field.However, the natural electromagnetic field has a wider frequency band range and weak signals, and these signals are easy to be disturbed by all kinds of electromagnetic noise in the actual measurement, so the interpretation level of the subsequent electromagnetic inversion method is seriously effected.In order to solve this problem, combining the adaptability of local mean decomposition (LMD) with the multi-resolution of wavelet, here the magnetotelluric noise suppression method based on local mean decomposition and wavelet threshold was proposed.First of all, LMD was used to divide a noisy signal into a number of product functiion (PF) components.Then, according to magnetotelluric signal-to-noise characters, PF1component was retained, the appropriate wavelet threshold was chosen to denoise the resteach PF component.Finally, the magnetotelluric useful signal was obtained with superposition and reconstruction.Using a computer to simulate typical strong interferences, the denoising performances of the proposed method were studied under the conditions of different wavelet functions, decomposition layers and threshold modes, and the method was applied to process the magnetotelluric data measured in ore concentration areas.The results showed that the proposed method can better extract the outline features of large-scale strong interferences superimposed on weak magnetotelluric signals, and the apparent resistivity curve is more smooth and continuous; the quality of magnetotelluric data is improved significantly in lower frequency bands.
local mean decomposition; wavelet threshold; magnetotelluric; noise suppression
国家自然科学基金(41404111; 41304098);国家863计划(2014AA06A602);湖南省自然科学基金(2015JJ3088);中国博士后科学基金(2015M570687)
2016-04-14 修改稿收到日期:2016-08-05
李晋 男,博士后,副教授,1981年生
彭冲 男,硕士生,1989年生
TN911.4; P631
A
10.13465/j.cnki.jvs.2017.05.021

