基于EEMD的舰船辐射噪声特征提取方法研究
李余兴,李亚安,陈 晓
(西北工业大学 航海学院,西安 710072)
基于EEMD的舰船辐射噪声特征提取方法研究
李余兴,李亚安,陈 晓
(西北工业大学 航海学院,西安 710072)
为了解决复杂海洋环境中水声信号的特征提取问题,提出了一种利用集合经验模态分解(EEMD)研究舰船辐射噪声特征提取的方法。对经验模态分解后的不同类别三类舰船辐射噪声信号各阶固有模态函数(IMF)中心频率可分性进行分析,并讨论了最强IMF中心频率特征参数。通过比较一定数量不同类别的舰船辐射噪声的最强IMF中心频率及高低频能量差特征参数发现,同类舰船的特征参数基本处于同一水平,不同类型的舰船存在一定差异。实验结果表明,采用EEMD的舰船辐射噪声信号的最强IMF中心频率作为特征参数相比高低频能量差特征参数对舰船具有较好的可分性。
集合经验模态分解; 固有模态函数; 舰船辐射噪声; 中心频率; 特征提取
舰船辐射噪声和海洋环境的复杂性使得从舰船辐射噪声中提取一种能反映目标特性的特征成为该领域的难题。传统的特征提取方法主要包括时域上的波形结构、频域上的经典谱估计、现代谱估计和高阶谱估计特征提取、以及时-频域上的短时傅里叶变换、小波变换等[1]。传统的特征提取方法具有一定的局限性,傅里叶变换分析不能很好的反映信号的时变特性,小波变换能同时提供信号的时-频信息,但受到小波基函数选择的限制。因此,传统的信号处理方法不适用于水声信号处理。
HUANG等[2-3]的经验模态分解(Empirical Mode Decomposition,EMD)方法是从信号本身的尺度特征出发对信号进行分解,没有固定的先验基底,是自适应的,得到的固有模态函数(Intrinsic Mode Function,IMF)通常可表现信号内含有的真实物理意义,因此能够较好地反映出系统的物理特性。随着EMD方法理论和实践的不断发展,EMD也在故障诊断领域[4-5]、生物医疗领域[6-7]、地球物理领域[8-9]、水声信号处理领域[10-11]得到广泛应用。但在实际应用中EMD会出现模态混叠现象,导致相邻的IMF波形混叠,相互影响,不利于对目标信号分析。EEMD方法是针对EMD方法的改进,它利用白噪声均匀分布的统计特性,对目标信号多次添加一定幅值的白噪声来降低模态混叠的影响。
近年来,胡桥等[12]利用基于EMD能量熵的方法实现水声目标检测;刘深等[13]提出一种基于IMF能量谱的水声信号特征提取方法,通过与小波能量谱法对比,证明该方法对水声信号具有较好的识别分类效果;杨宏等[14]采用EEMD方法对舰船辐射噪声进行能量分析,结果表明,以高低频能量差作为舰船辐射噪声的特征参数对舰船类别具有较好的可分性。这些方法的提出证明了经验模态分解用于水声信号目标检测及特征提取的可行性,但仅从能量角度进行分析,未考虑到目标的频率特性。
基于此,本文在EEMD及希尔伯特变换基础上,首先利用EEMD方法针对实测的不同类别的舰船辐射噪声进行模态分解,其次从频率及能量角度分析了各阶固有模态函数,讨论了最强IMF中心频率特征参数的可分性,最后将该方法与文献[14]中的高低频能量差特征参数比较,进一步证明基于EEMD的最强IMF中心频率特征参数可以较好的区分不同舰船类别。
1 EEMD及IMF中心频率
1.1 EMD算法
原始信号x(t),首先确定x(t)上所有的极值点,采用三次样条函数曲线对所有的极值点进行插值,从而拟合出原始信号x(t)的上包络线xmax(t)及下包络线xmin(t)。按顺序连接上、下两条包络线的均值即得一条均值线m1(t):
m1(t)=[xmax(t)+xmin(t)]/2
(1)
再用x(t)减掉m1(t)得到h1(t):
h1(t)=x(t)-m1(t)
(2)
判断h1(t)是否为满足IMF的条件,若不满足,则重复式(1)、(2)。若h1(t)满足了,则将h1(t)记为c1(t),并将其从原信号x(t)中去除。剩余分量变成一个新的x(t)并重复进行上述处理。最终,原信号可表示为
(3)
式中:cm(t)为第m个IMF,r(t)为最终的不再包含IMF的剩余分量,M代表IMF的总个数。判断是否为IMF时通常需要进行多次迭代运算,而终止条件可由
(4)
确定,即令相邻两次迭代的标准差小于阈值ε,本文取0.28。
1.2EEMD算法
为了解决模态混叠问题,WU等[15]提出了EEMD,它是一种噪声辅助信号处理方法。具体步骤如下:
(1) 对原始信号添加N次白噪声,生成N个新的x(t)。
(2) 对N个x(t)进行EMD得到N组IMF分量及余量。
(3) 对同阶的N个IMF取平均获得新的一组IMF分量。
(4) EEMD分解结果依然可以用式(3)表示,r(t)为原始信号去掉平均后所有IMF分量的余量。
依据参考文献[14]中的参数设定,本文对3类舰船辐射噪声进行EEMD分解时,选取白噪声标准差为0.3,集合样本数N取100。
1.3IMF中心频率
信号x(t)经EEMD分解后,对分解得到的IMF分量c(t)做希尔伯特变换,即
(5)
其解析信号定义为

(6)
(7)
目标信号被分解后的任意一阶IMF的瞬时频率总是围绕一个中心频率波动,定义这个频率为该阶IMF的中心频率。假设第m阶模态共有N个采样点,第n个采样点的瞬时频率为fmn,瞬时振幅为bmn,该点瞬时强度为
(8)
式中:Qmn为分解后的第m阶模态的第n个采样点的瞬时强度。原观测数据的第m阶固有模态函数中心频率为:
(9)

(10)
2 舰船辐射噪声信号IMF中心频率分析
2.1 舰船辐射噪声经验模态分解
对三类实测舰船辐射噪声信号进行仿真实验,采样频率44.1 kHz,数据长5 000点,每一类舰船噪声信号各100个样本。首先对数据进行归一化处理,得到三类舰船辐射噪声的时域波形,如图1所示。将归一化处理后的数据样本进行EMD分解,如图2所示,其中横坐标为采样点数,纵坐标代表归一化振幅。
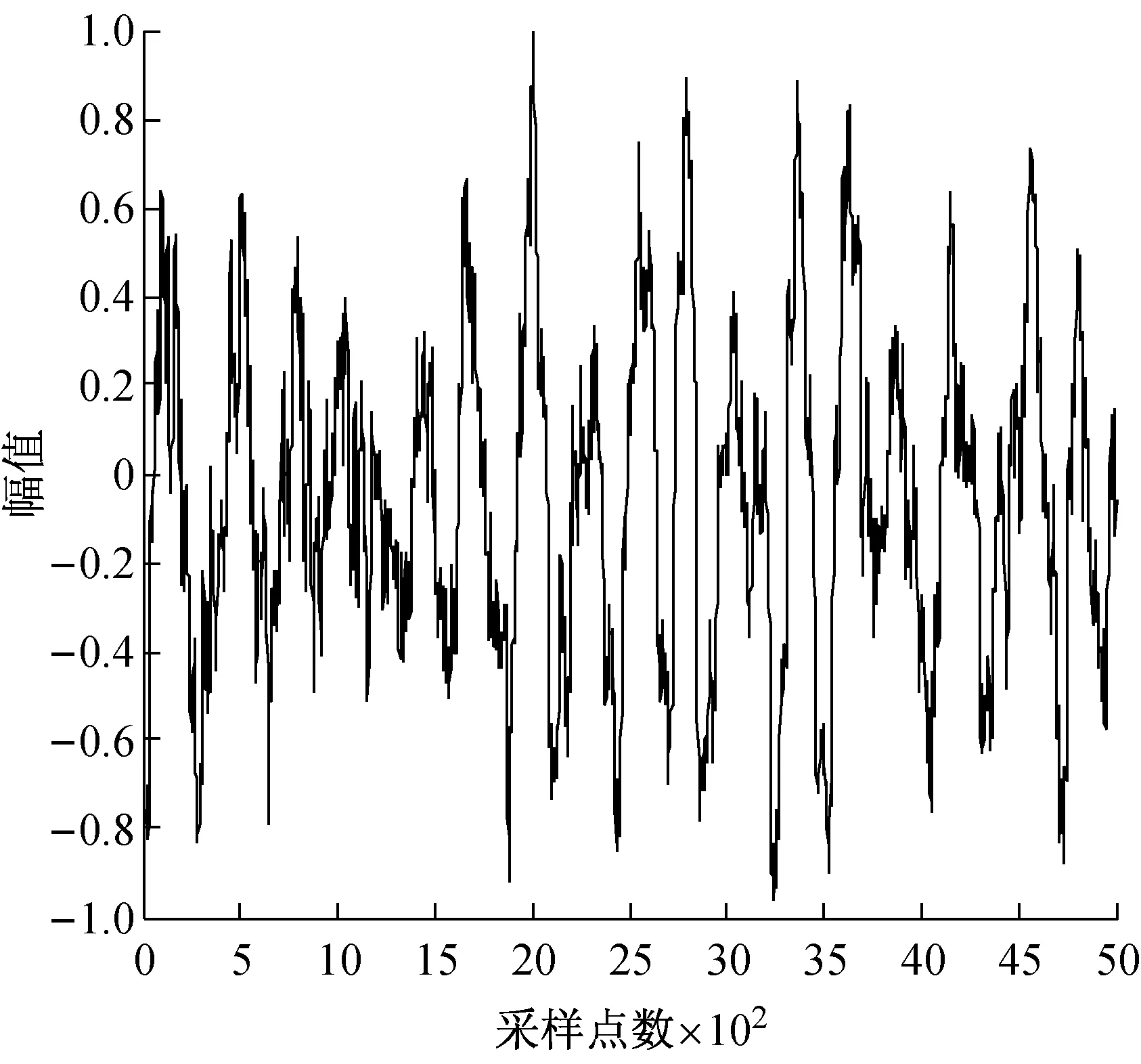
(a) 第一类舰船辐射噪声
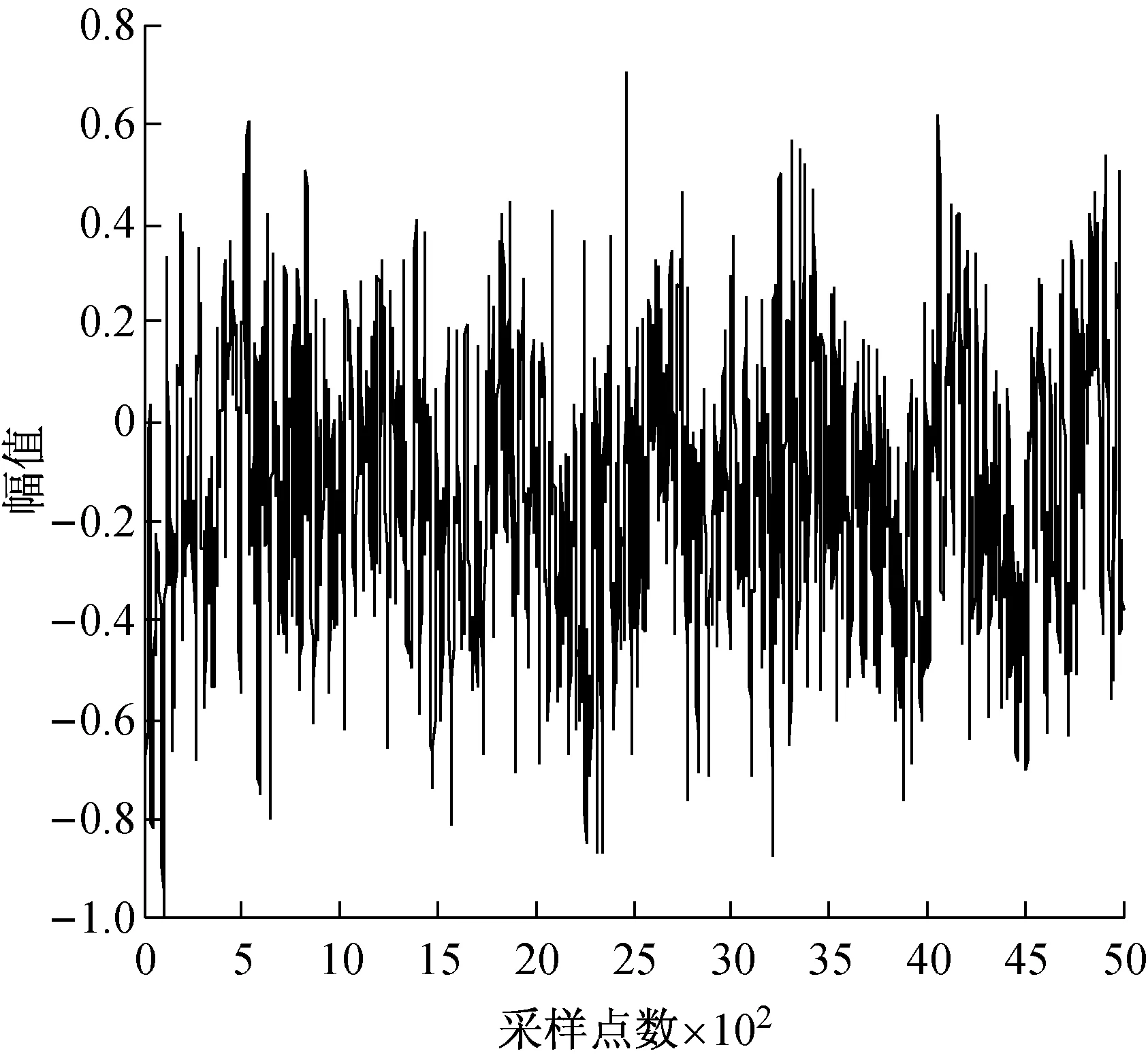
(b) 第二类舰船辐射噪声
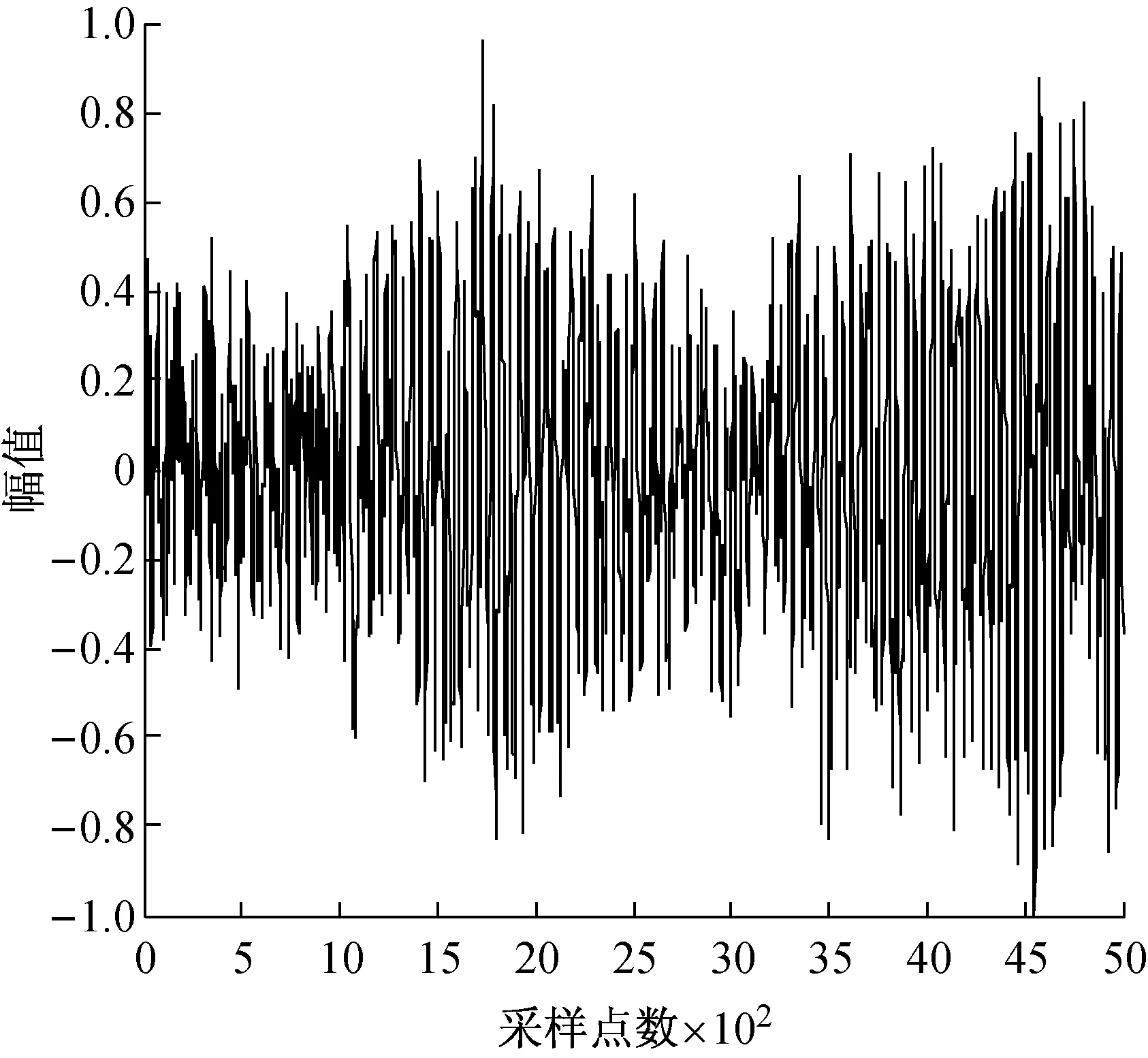
(c) 第三类舰船辐射噪声
由图2可以看出,经过EMD分解的舰船辐射噪声信号按从高频至低频次序依次分解为一组固有模态函数分量,其中三类信号的第一阶模态IMF1表示信号的最短振荡周期,通常为噪声分量或信号的高频分量。三类舰船噪声辐射信号的IMF阶数也不相同,IMF阶数取决于信号的复杂程度,即信号越复杂,分解得到的IMF阶数越多。每类舰船辐射噪声信号的IMF中总会有1个或几个IMF的幅值明显高于其它分量,通常这些IMF分量构成信号的主要能量成分,进而反映出信号的最显著特征。将各阶IMF分量作希尔伯特变换,可得到随时间变化,具有实际物理意义的瞬时频率。









(a) 第一类舰船辐射噪声







(b) 第二类舰船辐射噪声









(c) 第三类舰船辐射噪声
图2 三类舰船辐射噪声EEMD分解的各阶IMF
Fig.2 The results of EEMD method for three types of ship radiated noise
2.2 舰船辐射噪声IMF中心频率
将经过EMD分解的三类舰船辐射噪声信号按式(10)求得各阶模态的中心频率,图3横坐标为三类舰船辐射噪声信号1~8阶IMF,纵坐标表示各阶IMF对应的中心频率。由图3可以看出:三类信号的IMF中心频率随着IMF的增大而减小,符合EMD按从高频至低频次序依次分解的原理;三类信号的IMF1与IMF2中心频率均高于2 000 Hz,视为噪声模态;在3到8阶模态中三类信号的同阶中心频率非常接近,尤其是高阶模态。以上分析表明按EMD分解顺序排列的三类舰船辐射噪声信号的同阶IMF中心频率无明显的可分性。
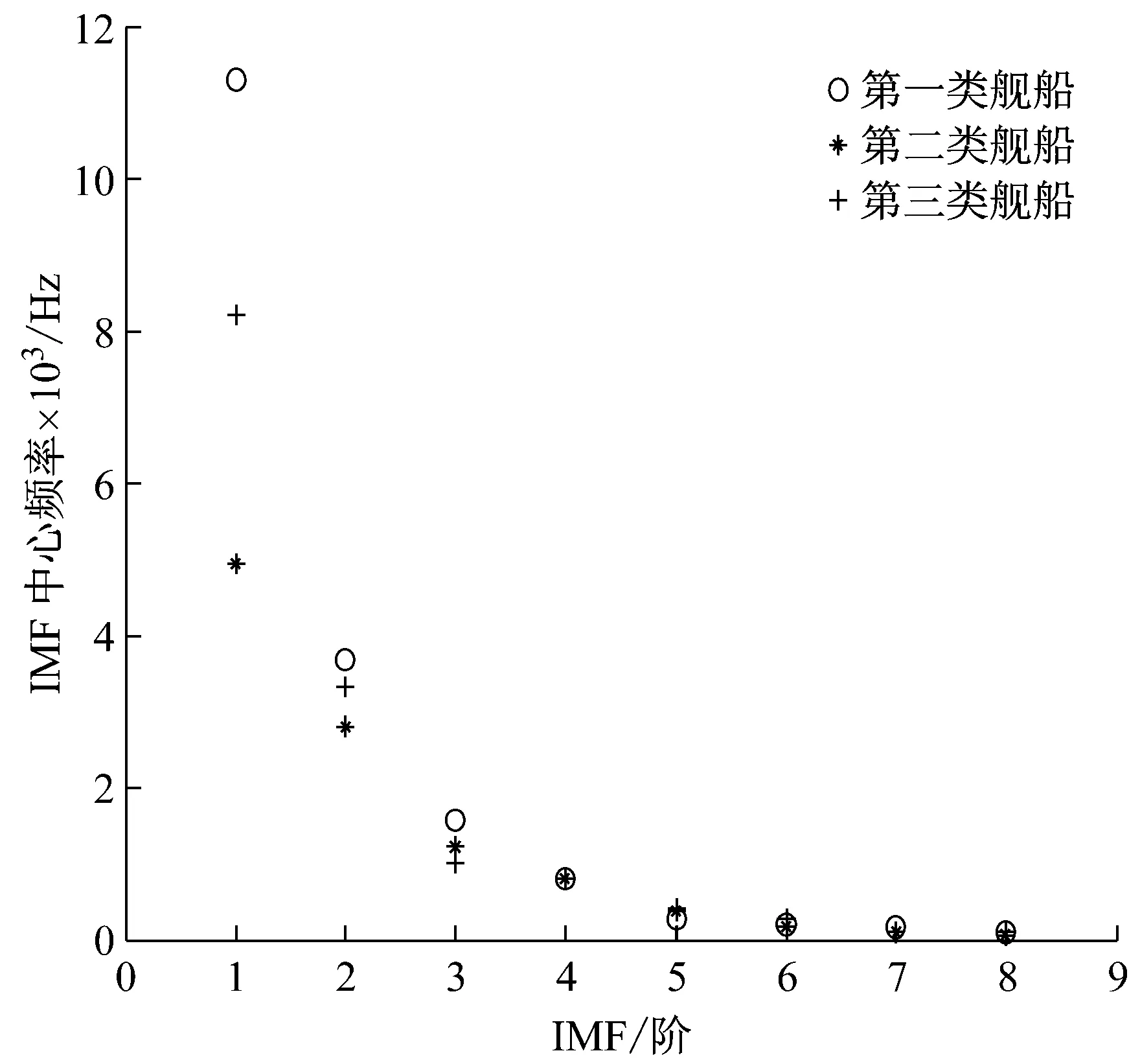
图3 三类舰船辐射噪声各阶IMF中心频率Fig.3 The center frequency of each IMF for three types of ship radiated noise
图4为去除噪声模态且以各阶IMF能量排序的三类舰船辐射噪声IMF中心频率图。第1阶IMF对应能量最强的模态,第6阶IMF对应能量最弱的模态。观察三类舰船辐射噪声IMF5与IMF6至少有2类信号的中心频率相近,而IMF3与IMF4相对IMF1与IMF2来说,其中心频率差异较小。IMF1与IMF2为能量最强的两个模态,能够反映原始信号的特征且中心频率存在明显差异,可作为三类舰船辐射噪声的特征参数进一步研究。
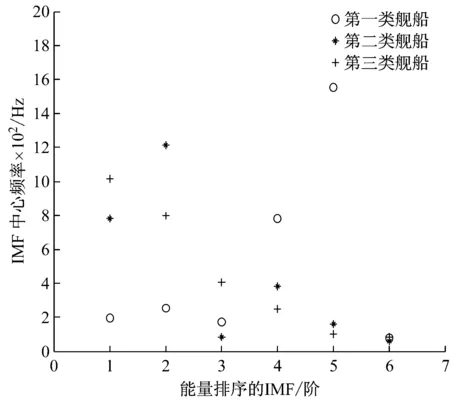
图4 三类舰船辐射噪声能量排序的IMF中心频率Fig.4 The center frequency of each IMF by energy ordering for three types of ship radiated noise
3 舰船辐射噪声特征提取方法研究
3.1 最强IMF中心频率
本文选取三类舰船辐射噪声中能量最强的IMF作为研究对象。若目标信号共分解为M阶模态,则定义平均强度最大的那一阶IMF的中心频率为最强IMF中心频率,即:
(11)
3.2 高低频能量差
[14]算法定义0~1 000 Hz为舰船信号的低频段,1 000~10 000 Hz为它的高频段,定义高频与低频段舰船辐射噪声能量差为舰船高低频能量差。表2给出了三类舰船单个样本的高低频能量差值,通过对比分析第一类舰船较其他两类舰船更容易区分,而第二、三类舰船能量差值相当,其可分性需要进一步分析。
表1 三类舰船辐射噪声信号的最强固有模态中心频率(每类1个样本)
Tab.1 The center frequency of IMF with the highest energy for three types of ship radiated noise.(each type only includes one sample)
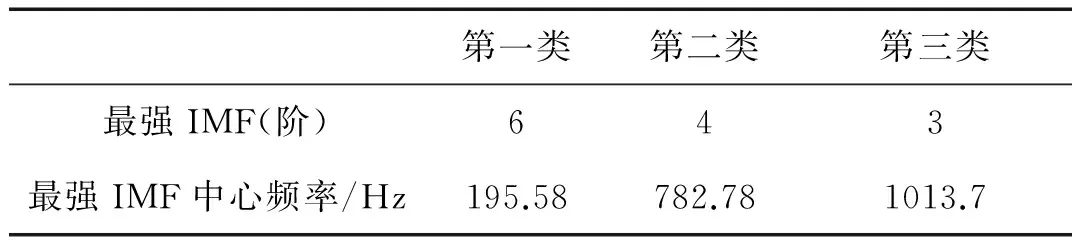
第一类第二类第三类最强IMF(阶)643最强IMF中心频率/Hz195.58782.781013.7
表2 三类舰船辐射噪声信号高低频能量差(每类1个样本)
Tab.2 The energy difference between the high and low frequency for three types of ship radiated noise.(each type only includes one sample)

第一类第二类第三类高低频能量差/dB-12.013-2.4347-1.5990
3.3 舰船辐射噪声特征提取方法比较
为验证样本最强IMF中心频率及高低频能量差作为特征参数对于三类舰船辐射噪声差异是否具有普遍性,在每一类信号的100个样本中随机抽取20个样本分别计算以上2个特征参数。图5中横坐标为样本数,纵坐标代表最强IMF中心频率。图5反映了信号优势频段的大小,同类舰船辐射噪声的最强固有模态中心频率在一定范围内波动,其数值基本处于同一水平,而不同类的舰船辐射噪声数值差异较大。
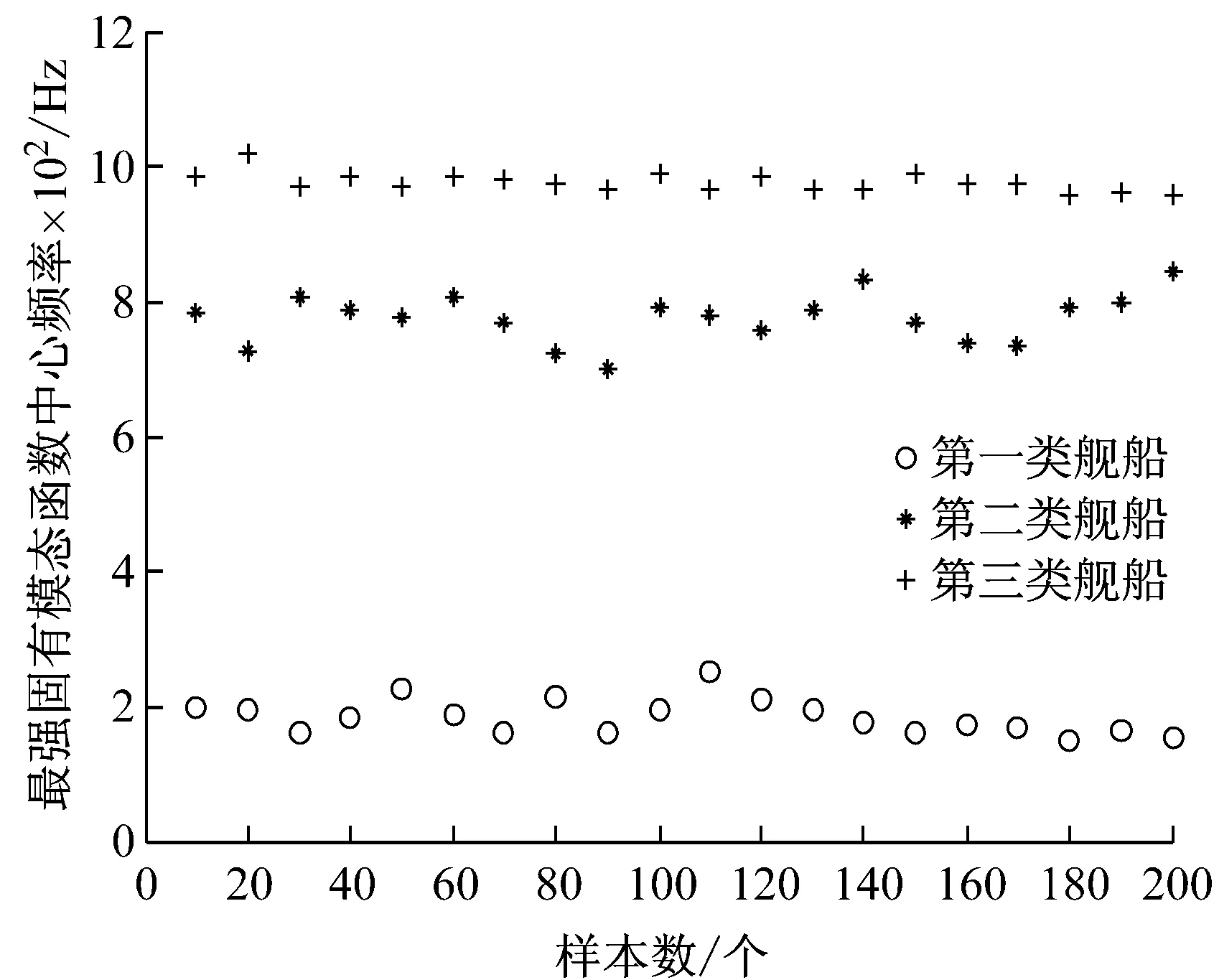
图5 三类舰船辐射噪声最强固有模态中心频率分布图Fig.5 The distribution of the most energetic center frequency of IMF for three types of ship radiated noise
图6表示三类舰船辐射噪声高低频能量差分布,它从宏观角度反映了高频和低频段舰船辐射噪声的能量差异。第一类舰船其高低频能量差绝对值最大且在同一水平波动,而其他两类舰船能量熵值较接近,可分性不明显。

图6 三类舰船辐射噪声高低频能量差分布图
Fig.6 The distribution of the energy difference between the high and low frequency for three types of ship radiated noise
表3进一步给出了每类20个样本舰船辐射噪声两种特征参数的波动范围及均值。三类舰船信号最强固有模态中心频率特征参数的均值有一定差异且波动范围无重叠频段。高低频能量差能较好的区别第一类舰船,其他两类舰船均值有一定差异但波动范围略有重叠,可分性差。以上结果表明最强IMF中心频率作为特征参数可较好的区分不同舰船类别。
表3 三类舰船辐射噪声信号的特征参数(每类20个样本)
Tab.3 The characteristic parameters for three types of ship radiated noise.(each type includes twenty samples)
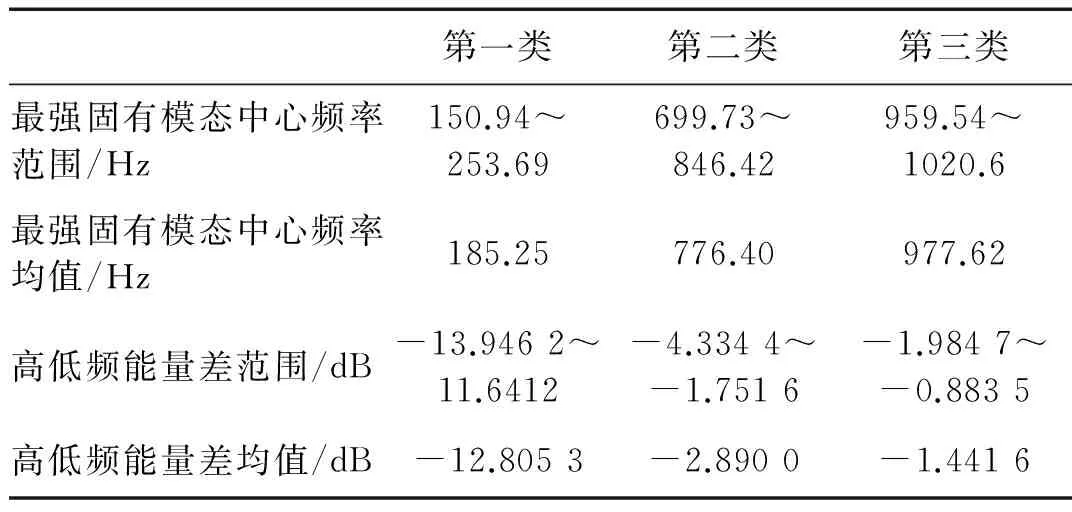
第一类第二类第三类最强固有模态中心频率范围/Hz150.94~253.69699.73~846.42959.54~1020.6最强固有模态中心频率均值/Hz185.25776.40977.62高低频能量差范围/dB-13.9462~11.6412-4.3344~-1.7516-1.9847~-0.8835高低频能量差均值/dB-12.8053-2.8900-1.4416
4 结 论
本文以EEMD为理论基础,研究了舰船辐射噪声IMF中心频率特征参数的提取。针对一定样本数量的三类不同舰船辐射噪声,分析了样本各阶IMF中心频率的可分性,从而确定以最强固有模态中心频率作为特征参数并进行了仿真实验,并与高低频能量差方法对比。结果表明:同类别的舰船辐射噪声具有相近的最强固有模态中心频率,不同类别的舰船辐射噪声的最强固有模态中心频率存在较大差异。相比高低频能量差方法,选取最强固有模态中心频率作为特征参数,能充分体现目标优势频段特征,具有较好的类别可分性。
参 考 文 献
[1] 李新欣.船舶及鲸类声信号特征提取和分类识别研究[D].哈尔滨:哈尔滨工程大学,2012.
[2] HUANG N E,SHEN Z,LONG S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London.Series A:Mathematical,Physical and Engineering Sciences,1998,454(1971):903-995.
[3] WU Z H,HUANG N E.A study of the characteristics of white noise using the empirical mode decomposition method[J].Proceedings of the Royal Society of London A,2004,2046(460):1597-1611
[4] 胡爱军.Hilbert-Huang变换在旋转机械振动信号分析中的应用研究[D].保定:华北电力大学,2008.
[5] 张志刚,石晓辉,陈哲明,等.基于改进EMD和滑动峰态算法的滚动轴承故障特征提取[J].振动与冲击,2012,31(22):80-83.
ZHANG Zhigang,SHI Xiaohui,CHEN Zheming.Fault feature extraction of rolling element bearing based on improved EMD and sliding kurtosis algorithm[J].Journal of Vibration and Shock,2012,31(22):80-83.
[6] 李小俚,崔素媛,Sleigh J W.基于希尔伯特黄熵的麻醉深度估计[J].中国生物医学工程学报, 2008,27(5):689-694.
LI Xiaoli,CUI Suyuan, SLEIGH J W.Estimation of Anesthetic Depth with Hilbert-Huang Entropy[J].Chinese Journal of Biomedical Engineering, 2008,27(5):689-694.
[7] WEI Q, LIU Q, FAN S Z.Analysis of EEG via multivariate empirical mode decomposition for depth of anesthesia based on sample entropy[J].Entropy, 2013, 15(9):3458-3470.
[8] 侯威, 封国林, 董文杰,等.利用排列熵检测近40年华北地区气温突变的研究[J].物理学报,2006,55(5):2663-2668.
HOU Wei,FENG Guolin,DONG Wenjie, et al.A technique for distinguishing dynamical species in the temperature time series of north China[J].Acta Physica Sinica,2006,55(5):2663-2668.
[9] 薛春芳,侯威,赵俊虎,等.集合经验模态分解在区域降水变化多尺度分析及气候变化响应研究中的应用[J].物理学报,2013,62(10):496-503.
XUE Chunfang,HOU Wei,ZHAO Junhu.The application of ensemble empirical mode decomposition method in multiscale analysis of region precipitation and its response to the climate change[J].Acta Physica Sinica,2013,62(10):496-503.
[10] 高云超.希尔伯特-黄变换在水声信号处理中的应用研究[D].哈尔滨:哈尔滨工程大学,2009.
[11] 李秀坤,谢磊,秦宇.应用希尔伯特黄变换的水下目标特征提取[J].哈尔滨工程大学学报,2009,30(5):542-546.
LI Xiukun,XIE Lei,QIN Yu.Underwater target feature extraction using Hilbert-Huangtransform[J].Journal of Harbin Engineering University,2009,30(5):542-546.
[12] 胡桥,郝保安,吕林夏,等.一种新的水声目标辐射噪声特征提取模型[J].鱼雷技术,2008,16(6):38-43.
HU Qiao,HAO Baoan,LÜ Linxia.Feature extraction model for underwater target radiated noise[J].Torpedo Technology,2008,16(6):38-43.
[13] 刘深,张小蓟,牛奕龙,等.基于IMF能量谱的水声信号特征提取与分类[J].计算机工程与应用,2014,50(3):203-206.
LIU Shen, ZHANG Xiaoji, NIU Yilong.Feature extraction and classification experiment of underwater acoustic signals based on energy spectrum of IMF’s[J].Computer Engineering and Applications,2014,50(3):203-206.
[14] 杨宏,李亚安,李国辉,等.基于集合经验模态分解的舰船辐射噪声能量分析[J].振动与冲击,2015,34(16):55-59.
YANG Hong,LI Yaan,LI Guohui.Energy analysis of ship radiated noise based on ensemble empirical mode decomposition[J].Journal of Vibration and Shock,2015,34(16):55-59.
[15] WU Z H,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
Ships’ radiated noise feature extraction based on EEMD
LI Yuxing,LI Yaan,CHEN Xiao
(School of Marine Science and Technology, Northwestern Ploytechnical University, Xi’an 710072, China)
In order to solve the feature extraction problem of underwater acoustic signals in complex ocean environment, a new method for feature extraction of ships’ radiated noise was proposed based on the ensemble empirical mode decomposition(EEMD).Three different types of ship radiated noise were chosen to perform the center frequency and energy analyses for their intrinsic mode functions (IMF).It was shown that the center frequencies of IMF are different from that of the IMF with the highest energy, so the center frequency characteristic parameters of the IMF with the highest energy can be applied to extract ships’ radiated noise features.By comparing the center frequency of the IMF with the highest energy and the energy difference between high frequency energy and low frequency one for a certain number of signals of different types ships’ radiated noise, it was shown that the center frequency of the IMF with the highest energy is at the same level for similar ships, but there is an obvious difference for different types of ships.The test results showed that the center frequency of the IMF with the highest energy as a characteristic parater is better than the energy difference between high frequency energy and low frequency one befor ships’radiated noise feratute extraction.
ensemble empirical mode decomposition; intrinsic mode function; ship radiated noise; center frequency; feature extraction
国家自然科学基金(51179157; 51409214; 11574250)
2016-07-01 修改稿收到日期:2016-08-03
李余兴 男,博士生,1984年7月生
李亚安 男,博士,教授,博士生导师,1961年6月
TN911.72
A
10.13465/j.cnki.jvs.2017.05.018

