近断层地震动作用下大跨度曲线刚构桥台阵试验研究

李 晰，贾宏宇，李 倩

(1.西南交通大学 土木工程学院，成都 6100312.西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031)

近断层地震动作用下大跨度曲线刚构桥台阵试验研究

李 晰，贾宏宇，李 倩

(1.西南交通大学 土木工程学院，成都 6100312.西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031)

为了研究近断层地震动对大跨度曲线刚构桥抗震性能的影响，以某一大跨度曲线刚构桥为原型，设计制作1/40缩尺比例模型，选取同一地震中的近断层地震动记录和远场地震动记录，利用多子台积木式模拟振动台台阵系统，完成了横向、纵向、横向+纵向一致输入及行波输入的对比试验。研究结果表明：近断层地震动中所含的速度脉冲会对曲线刚构桥的动力响应产生显著影响，并且行波效应会进一步提升其对结构响应的放大作用；近断层效应的放大作用对刚度较大的结构或者结构某一个方向更为明显，而行波效应对结构的影响主要取决于由多点激励所激发的高阶反对称模态；与直线桥相比较，曲率半径会增大曲线梁桥的水平刚度，从而使近断层效应和行波效应对曲线桥的动力响应产生更不利的影响。因此，在靠近断层的区域遭受同样的地震作用，曲线梁桥将产生更为严重的破坏，建议在抗震设计中应特别注意处于断层附近的曲线桥结构。

近断层地震动；曲线刚构桥；振动台试验；动力响应

由于曲线梁桥对地形有着良好的适应能力，为了跨越深沟峡谷并适应复杂的地形，中国西南山区的高等级公路及铁路系统中存在大量曲线梁桥。而中国的西南山区属于强震多发区且分布多条断裂带，如龙门山断裂带、鲜水河-小江断裂带[1]，因此该区域的大部分曲线梁桥可能会面临近断层地震动的威胁，如在2008年汶川地震中曲线段遭到严重破坏的百花大桥，除了结构本身的因素外，近断层效应被认为是其倒塌的主要因素之一[2]。因此有必要对近断层地震动作用下曲线梁桥的抗震性能进行更为深入的研究。

与远场地震动记录相比，近断层地震动记录的主要特点表现为具有较大的加速度峰值和明显的长周期速度脉冲[3]。有关近断层地震动的研究最早始于1958年，HOUSNER等[4]分析了在Port Hueneme地震中获得的第一条含有脉冲的强震记录，指出由于大部分的地震能量都包含在该地震中的一个脉冲里，使其地震动加速度峰值和反应谱值均要明显大于发生在太平洋沿岸相同等级的其它典型地震动。在随后的几次大地震(如1971年的San Fernando地震，1994年的Northridge地震、1995年的Kobe地震、1999年的Turkey地震、1999年的Chichi地震以及2008年的汶川地震)中，靠近断层附近的结构发生了比较严重的破坏，这使与近断层地震动相关的工程问题逐步被研究者所重视。BERTERO等[5]以一座在San Fernando地震中遭到严重破坏的建筑结构为例，最先研究了近断层地震动对结构响应的影响，分析结果表明近断层地震动中所含的脉冲是导致建筑发生破坏的主要原因。在此之后，很多学者进一步研究了近断层地震动对建筑结构响应的影响。这些已有研究表明当前的抗震设计规范均不能很好的体现近断层地震动对结构响应的影响[6]，近断层地震动中所包含的脉冲会对结构的响应产生较大的影响，特别是当脉冲周期与结构自振周期比较接近时[7]。同时这些研究还指出遭受近断层地震动的建筑结构会产生比远场地震作用下更大的基底剪力、层间位移[8]，从而导致结构变形需求的增加[9-10]。

与建筑结构类似，近断层地震动作用下桥梁结构的抗震性能同样引起了很多学者的关注，不同学者针对不同类型的桥梁结构及其构件进行了研究，如：简支梁桥[11]、连续梁桥[12]、刚构桥[13]、斜拉桥[14]、隔震桥梁[15-16]、桥墩[17]、伸缩缝[18]及桥台剪力键[19]等，以上这些研究均表明桥梁结构及其构件在近断层地震动作用下的动力响应与其在远场地震作用下的响应相比有比较明显的区别。PHAN等[20-21]通过振动台试验分别研究了桥墩和整体桥梁结构在近断层地震动作用下的动力响应后也得了出类似结论。PHAN指出相对于远场地震动，遭受近断层地震动作用的桥墩将产生更大的变形。SAIIDI指出近断层地震动将会影响桥梁结构发生损伤的类型及位置。从上面所提到的已有研究可以看出近断层地震所包含的脉冲特性可能会给桥梁结构带来与抗震设计规范所预测的不同的危害。但以上研究均以直线型桥梁为研究对象，缺少对曲线型桥梁的研究，并且这些研究主要基于数值模拟分析，缺乏振动台试验的验证。

鉴于此，本文以某一大跨度曲线刚构桥为例，按照1/40的比例设计制作缩尺模型，并选取典型的近断层地震动记录和远场地震记录作为地震输入，对比研究了大跨度曲线刚构桥在近断层地震动作用下的动力响应特点。

1 模型概况

试验原型为一座5跨预应力钢筋混凝土连续刚构桥，桥跨布置为68 m+120 m×3+68 m，桥宽12 m。整桥位于平曲面上，平面曲率半径R=620 m。上部结构为变截面单箱单室预应力钢筋混凝土箱梁，下部结构采用双薄壁墩。考虑到实验室空间和振动台实际承载能力，试验模型的几何缩尺比为原型的1/40，试验模型布置如图1所示。

1.1 相似设计

本次试验的模型材料选用有机玻璃，其与原型桥梁中混凝土材料的参数对比见表1。此外，根据实验室的场地条件，选取1∶40的比例尺对原桥进行缩尺。由于试验主要研究曲线梁桥在水平地震激励下的动力响应，因此模型的相似设计采用忽略重力影响的附加人工质量强度模型，并假设：①竖向力不会对结构的横向刚度产生影响，即刚度相似关系满足Sk=SESL；②模型桥的应变与原型桥相等，即应变的相似系数Sε=1；③有机玻璃的阻尼比小于钢筋混凝土材料，即Sζ=0.6。基于以上假设和模型试验相似理论的量纲分析法[22]，各物理量的相似关系见表2。

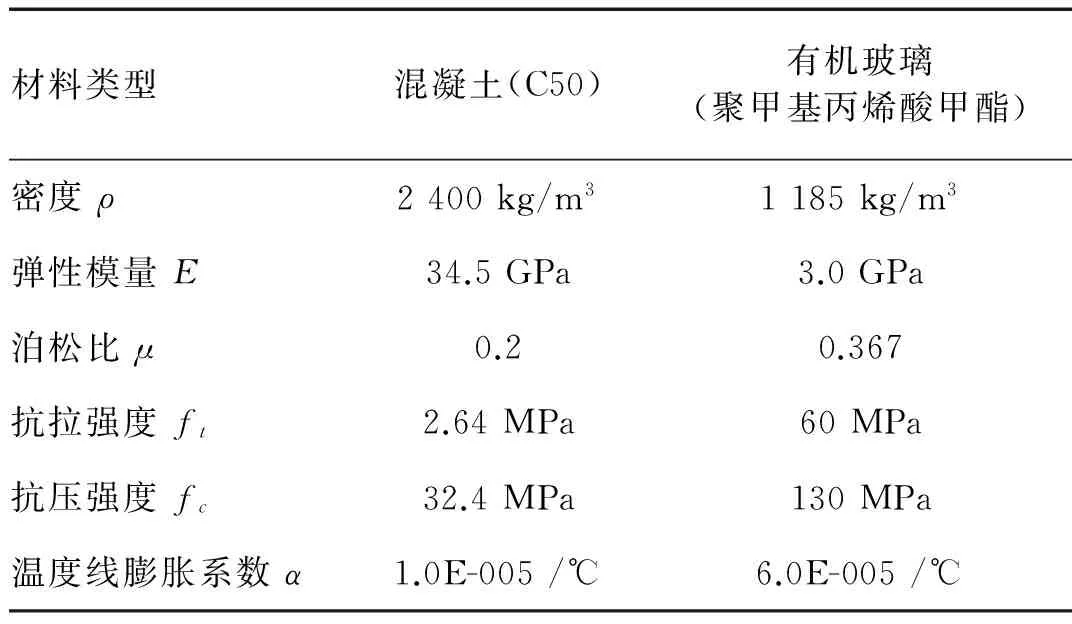
表1 材料参数对比Tab.1 Comparison of material parameters

当模型材料和几何相似比确定后，模型其它重要物理量的相似系数，如加速度幅值相似系数、时间相似系数以及质量相似系数，主要取决于等效质量密度ρE的相似系数SρE。等效质量密度的取值会影响附加人工质量的大小以及时间相似系数的大小。过大的等效质量密度会使附加人工质量过大从而超出振动台和模型的承载能力，而过小的等效质量密度会使相似后的地震动输入持时过短。因此综合考虑以上因素后，SρE取1.72。其中试验模型所需的附加人工质量由式(1)确定：

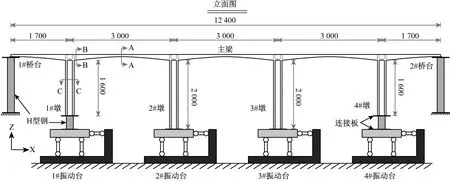
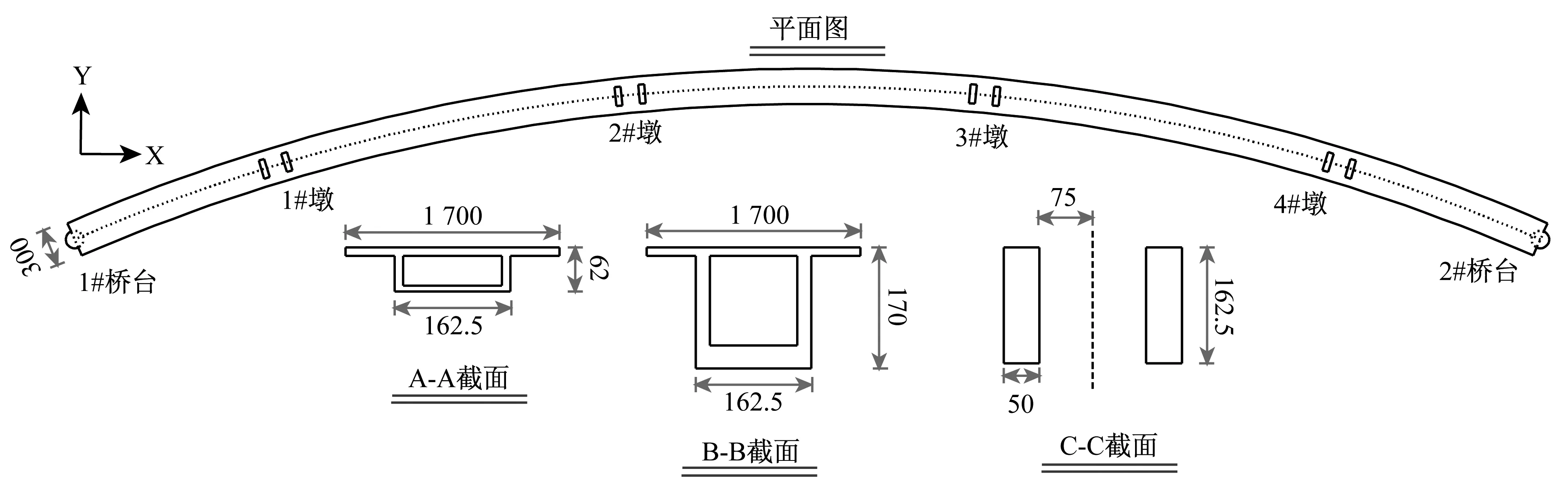
图1 模型桥布置图(mm)Fig.1 Schematic view of the test curved rigid bridge (mm)

(1)

式中：mad为附加的人工质量；mp为原型结构总质量；SρE为等效质量密度相似系数；Sρ为无附加人工质量时模型的质量密度相似系数(简称质量密度相似系数)；SL为几何相似系数。依据式(1)、表1和表2经计算可得所需附加人工质量为683.4 kg。

1.2 模型制作

模型采用有机玻璃制作，主要分为主梁、桥墩、连接构件三个部分。对于主梁部分，为了降低制作的复杂性，首先，将截面尺寸连续变化的梁体分为3段，如图2(a)所示，其中A-B段(A-A截面至B-B截面)的顶板厚度为12 mm，底板厚度8 mm，腹板厚度12 mm，梁高固定为62 mm；B-C段(B-B截面至C-C截面)的顶板厚度为12 mm，底板厚度10 mm，腹板厚度12 mm，梁高从62 mm线性变化到81 mm；D-E段(D-D截面至E-E截面)的顶板厚度为12 mm，底板厚度10 mm，腹板厚度15 mm，梁高固定从81 mm线性变化到170 mm。其次，忽略箱梁截面内外侧倒角以及上翼缘的厚度变化，按照抗压抗弯刚度相等的原则对原型桥的截面进行简化，图2(a)给出了B-B截面简化示意图，其他截面类似。此外，设计制作了如图2(a)所示的连接构件，用来a)连接桥墩和振动台；b)模拟桥台及不同墩高。其中，桥台处连接构件高度为200 mm，1号和4号桥墩处的连接构件高度为40 mm，2号和3号桥墩直接采用一块连接板与振动台相连接。实际安装完毕的模型如图2(b)所示。

表2 模型相似需求Tab.2 Similitude requirements

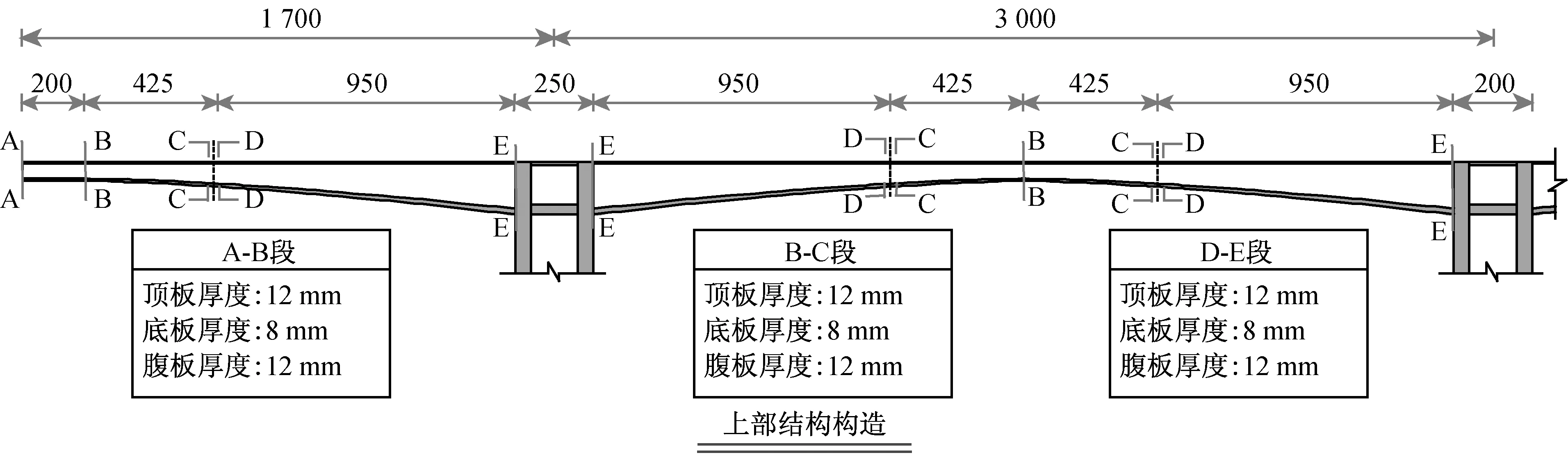
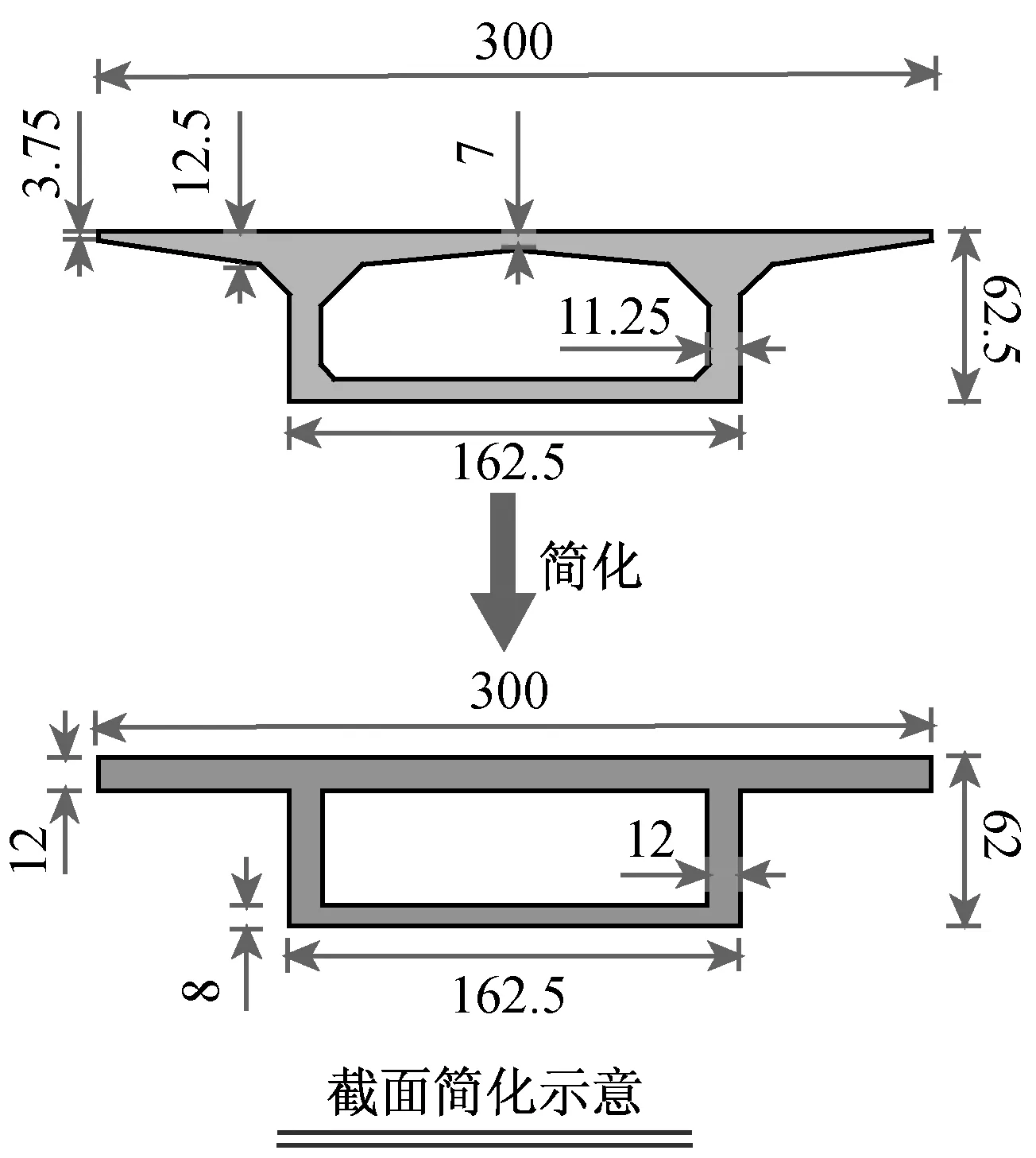
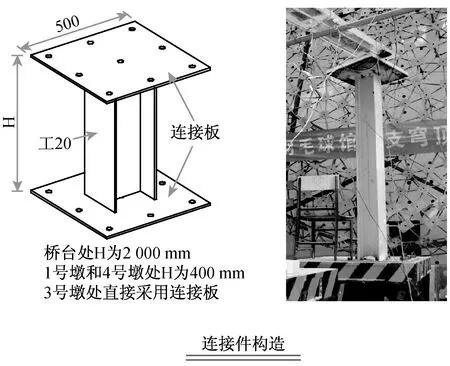
(a) 模型制作示意图(mm)

(b) 实际模型示意图

1.3 振动台及传感器布置

本次试验使用振动台台阵系统来完成曲线梁桥模型的一致及非一致输入。该台阵系统由4个台面尺寸为1 m×1 m的独立振动台组成，并按照曲线模型桥的线形进行布置，如图3(a)所示。

试验过程中主要完成对加速度及位移的测量，其中加速度测量采用单向ICP(Integrated Circuits Piezoelectric)加速度传感器(量程：±5 g)，主要布置在墩顶及跨中，共计8个径向传感器，1个切向传感器；径向位移测量采用941B型位移传感器(量程：±200 mm，频率范围：0.25～100 Hz)，主要布置在桥墩顶部和底部，共计8个传感器；纵向相对位移测量采用拉线位移计(量程：±250 mm)，布置在模型第三跨处，共计1个传感器。图3(b)给出了试验模型传感器详细布置图。此外，所有传感器的信号采集均使用IMC(Integrated Measurement and Control)动态数据采集系统，采样频率为1 000 Hz。

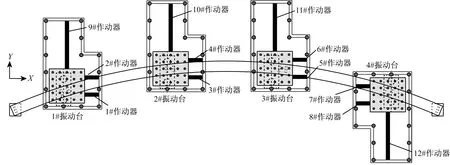
(a) 振动台布置图

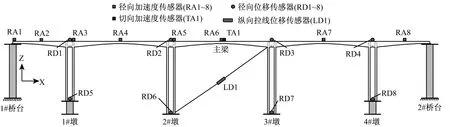
(b) 传感器布置图

2 地震波的选取与工况设置

试验用地震波均为来自PEER(Pacific Earthquake Engineering Research)地震数据库的实际地震记录。为了减少其它因素的影响，突出近断层地震动中所含速度脉冲的影响，本文选取地震动的标准为：①同一地震(Chi-Chi 地震，1999)；②记录点场地条件相同；③将所选地震动加速度峰值调整为相同的值。依据此原则，共选择两条地震记录，其中一条为含有速度大脉冲的典型近断层地震动记录(TCU068)。此外，依据NEHRP场地分类标准[23]，测点的场地条件均为C类场地(360 m/s≤Vs30≤760 m/s)。地震波详细信息如表3所示。

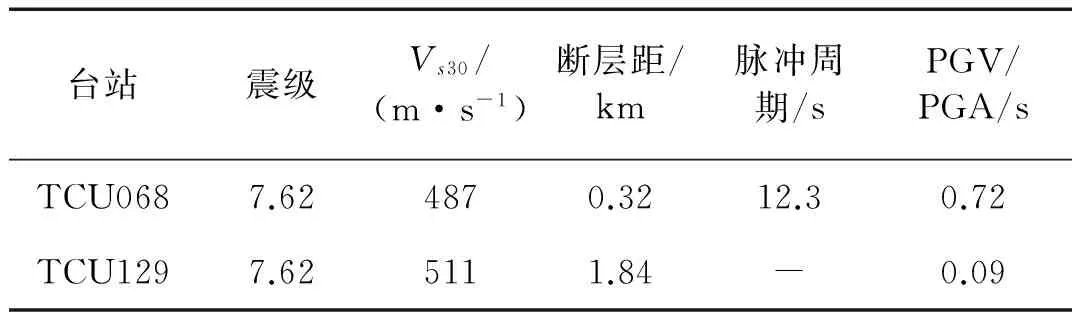
表3 选用的地震动的特征Tab.3 Details of the selected ground motions

由于本文的主要目的是研究近断层地震动中所包含的脉冲对大跨曲线刚构桥动力响应的影响，同时依据《公路桥梁抗震设计细则》(JTG/T B02-01—2008)，原桥属于A类桥梁，按照8度设防，故将所选原始地震波的加速度峰值PGA均调整为0.2g。调整后的地震动时程曲线及加速度反应谱如图4所示。从图4(a)可以看出，所选近断层地震动记录包含明显的速度脉冲，依据BAKER[24]给出的脉冲周期估算方法可知其脉冲周期Tp为12.3 s，并且从表3可以看出与远场地震相比其具有较大的PGV/PGA比值。从图4(c)还可以看出，由于近断层地震动包含速度脉冲，当反应谱的周期大于0.3 s后，近断层地震动记录的反应谱谱值要明显大于远场地震动的谱值[6]。

对于缩尺模型的振动台试验而言，地震作用输入时需要根据加速度幅值相似比将水平加速度峰值调整到0.4g，并按照频率相似比对地震波进行压缩，同时根据振动台的频带输入范围，将压缩后的地震波进行滤波，滤波范围为0.1～50 Hz。基于所选地震波，本试验的地震激励分为一致和非一致激励两类，地震输入方向为纵向(X向)、横向(Y向)及横向+纵向(X+Y向)。具体试验工况见表4。为了模拟行波效应对各个墩底带来的时间迟滞，假设地震动从1号振动台向5号振动台传播，相邻振动台作动器接受指令的时间差Δt=D/Vapp，其中D为相邻振动台的间距，Vapp为假设的视波速。此外，为了使时间迟滞较为明显，采用了较小的视波速，即Vapp=300 m/s。

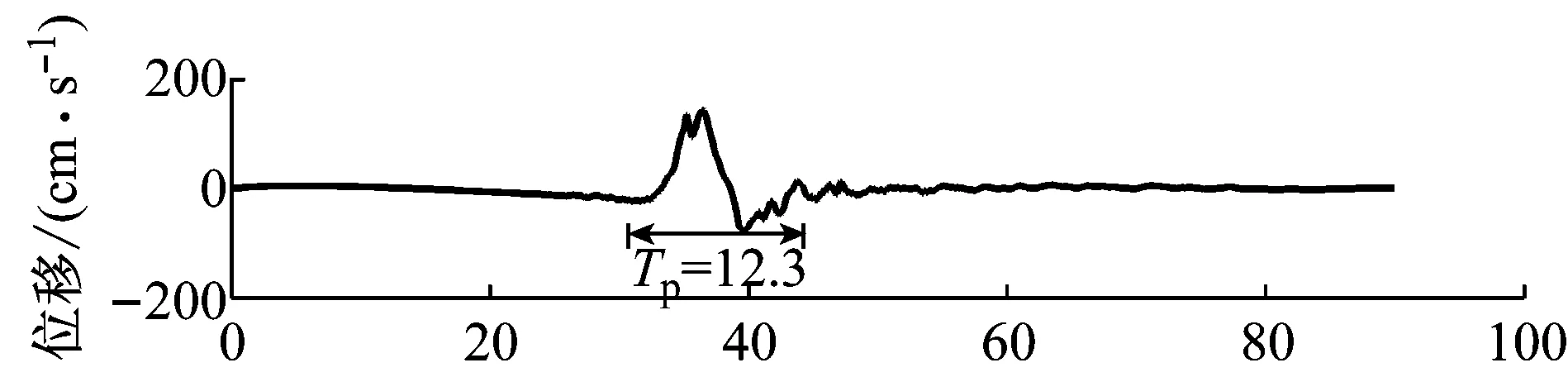
(a) TCU068地震时程

(b) TCU129地震时程

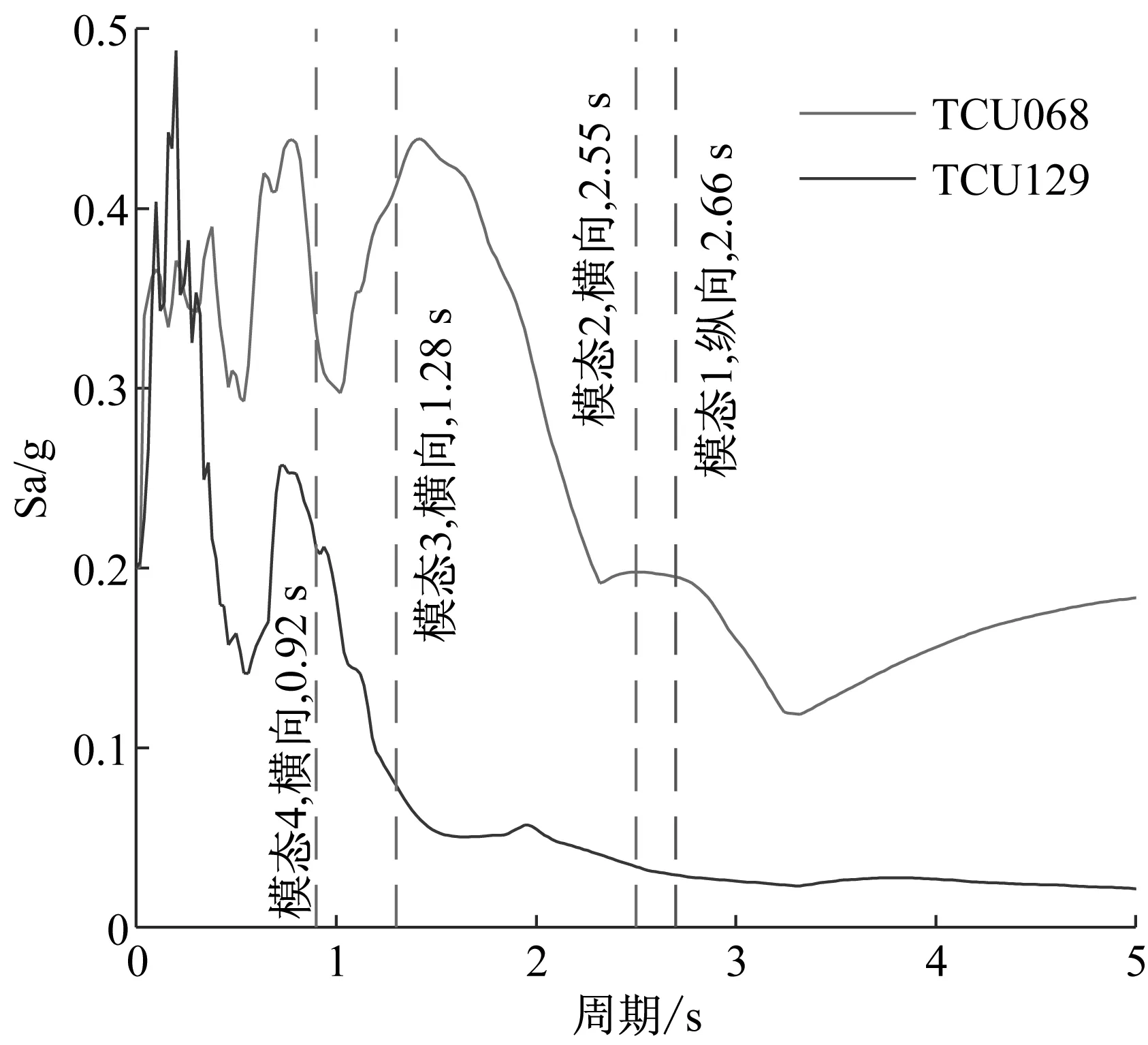
(c) 反应谱对比图

Fig.4 Time histories and acceleration response spectra for selected ground motions

表4 试验工况设置Tab.4 Shake-table test cases

3 试验模型动力特性

本试验采用FDD(Frequency Domain Decomposition)法识别了模型在白噪声激励(X+Y向)下的模态信息。切向加速度传感器和径向加速度传感器的功率谱矩阵的奇异值如图5(a)所示。从图5(a)可以看出，共识别出了模型的前4阶模态信息，其频率及振型如图5(b)所示。模型的1阶模态(3.38 Hz，纵漂)与2阶模态(3.52，横向对称)较为接近，说明模型桥的纵向整体刚度与横向整体刚度较为接近，这可能是由于墩梁固结及主梁弯曲造成的。此外还可以看出，模型的第3阶模态(7.03)和第4阶模态(9.77)分别为横向反对称和正对成模态。如果这些模态被激发，结构的横向反应将取决于这些模态的共同作用。

4 试验结果分析

基于第2节所选的地震波及工况设置，分别通过振动台试验对近断层地震动作用下的大跨曲线刚构桥抗震性能进行了研究。为了明确近断层效应的影响，定义放大系数AFN=RN/RF，其中RN为桥梁结构在近断层地震动作用下的响应；RF为桥梁结构在远场地震作用下的响应。同样为了明确非一致近断层地震动激励对结构响应的影响，定义放大系数AFW=RVapp/R，其中RVapp为结构在视波速为300 m/s的非一致地震激励下的响应；R为结构在一致激励下的响应。

此外，由于结构的变形(如桥墩的相对位移)能够比较直接的反映结构及其构件的破坏程度，所以当前的抗震设计规范均把变形作为一个重要的抗震指标，并且在振动台试验测试中，变形值的测量要比强度值更为精确。因此，本文中在振动台试验结果中只给出了桥墩相对位移的测量结果。

4.1 近断层效应

如图6所示，相对于远场地震动，在近断层地震动作用下曲线刚构桥各桥墩的切向和径向相对位移都明显增大。桥墩切向相对位移在单向及双向激励下放大系数的最大值分别为1.83和1.50，桥墩径向相对位移在单向及双向激励下放大系数的最大值分别为5.37和3.64(如表5所示)。这些结果都说明近断层地震动会对大跨度曲线刚构桥的抗震性能产生不可忽视的影响，如果在抗震设计中不考虑近断层效应，将有可能严重低估桥梁结构在地震中所发生的破坏。产生这种现象的原因可以主要归结为近断层地震动中所含速度大脉冲对反应谱谱值的放大作用(如图4(c)所示)，其他学者在相关研究中也得到了类似的结论[25-26]。

依据表2的相似关系，将通过测试识别出来的模型桥模态信息(如图5所示)转化为原桥的模态信息，如图4(c)所示，其前4阶振动周期分别为2.66 s、2.55 s、1.28 s和0.92 s，其中第1阶为纵向振动，第2～4阶为横向振动。从图4(c)可以看出，对于本文所选的地震波当反应谱周期大于0.3 s时，近断层地震动的反应谱值要明显大于远场地震动，特别是当反应谱周期在1.3～3 s之间时，不但近场地震动反应谱的谱值要大于远场地震动，其谱值之比随着周期的减小而增大。当结构的基频处于这个区间范围时，相对于远场地震，近断层地震动不但会放大结构的响应，而且会对刚度更大的结构或者结构的某一方向产生更为明显的影响。因此，由于模型桥横向刚度要大于纵向刚度，使近断层地震动对桥墩径向位移的放大作用要明显大于切向位移，其放大系数最大值分别为5.27和2.71(如表5所示)。

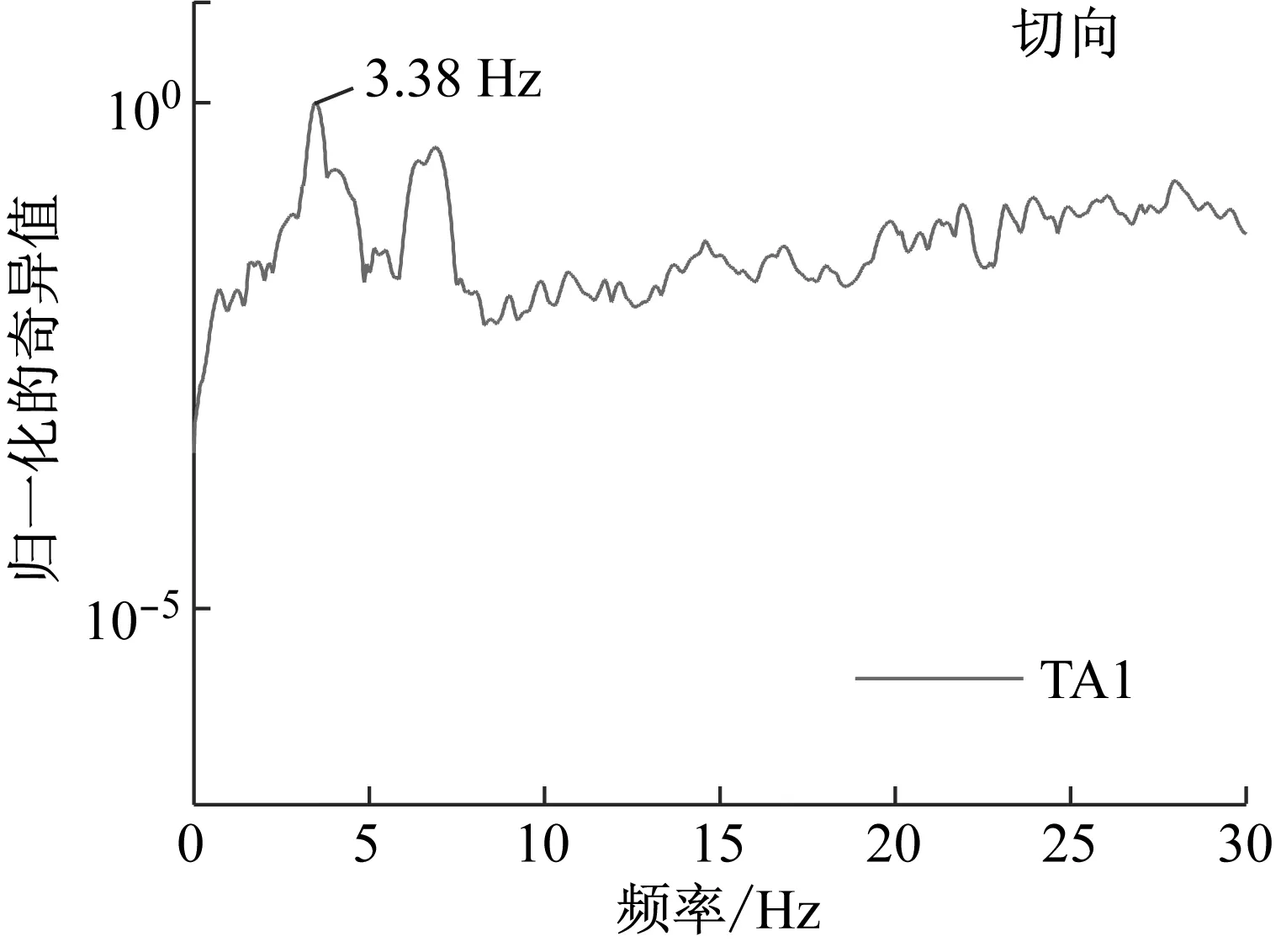
(a) 测试所得的功率谱密度奇异值

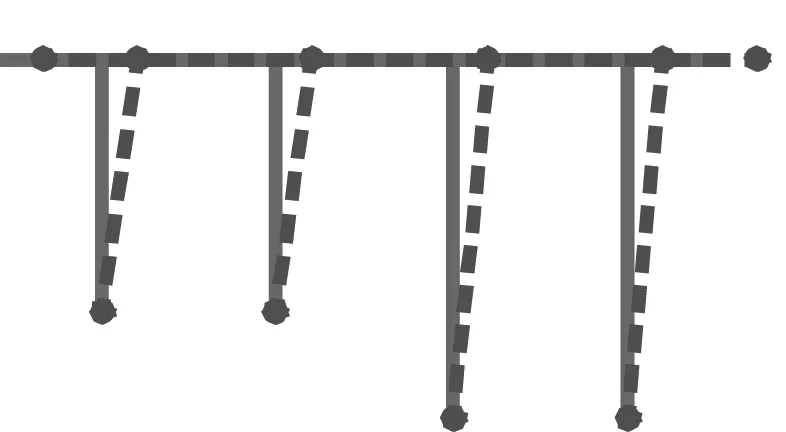
模态1:3.38 Hz,纵漂

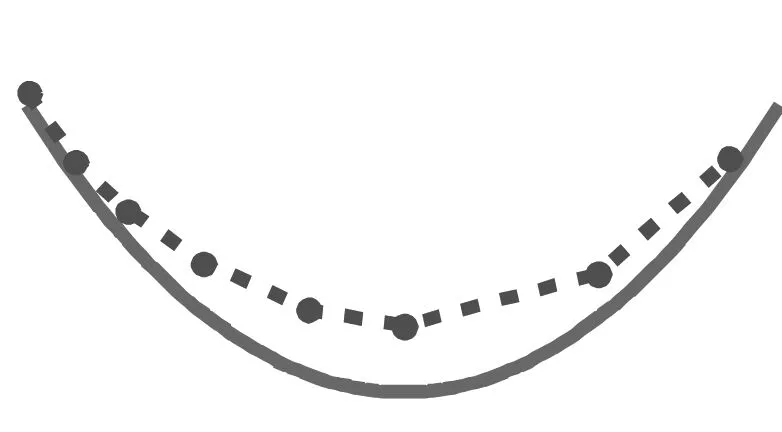
模态2:3.52 Hz,横向正对称

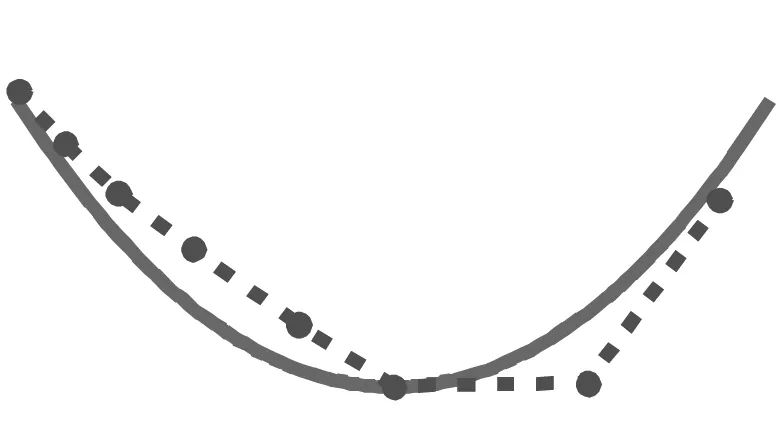
模态3:7.03 Hz,横向反对称

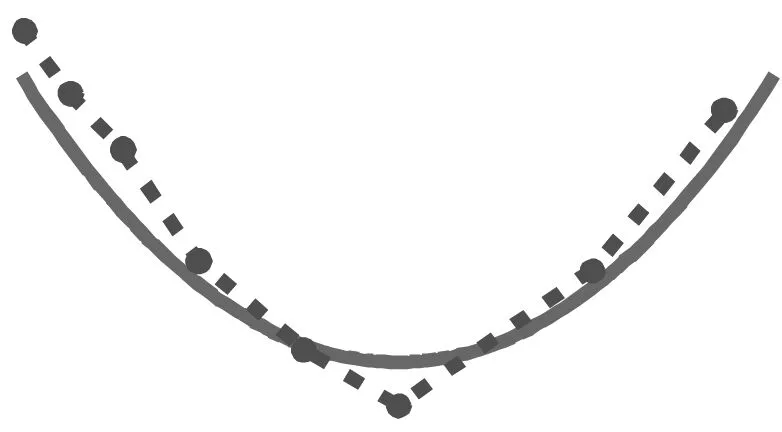
模态4:9.77 Hz,横向正对称

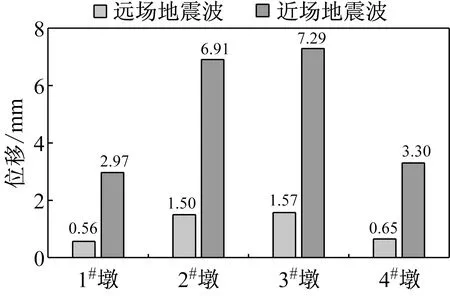
(a) Y向激励下的径向位移

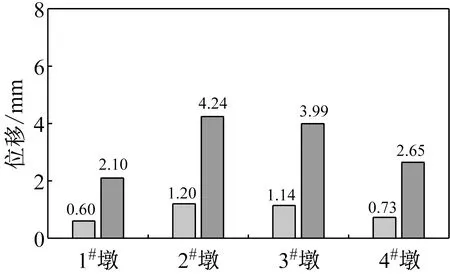
(b) X+Y向激励下的径向位移

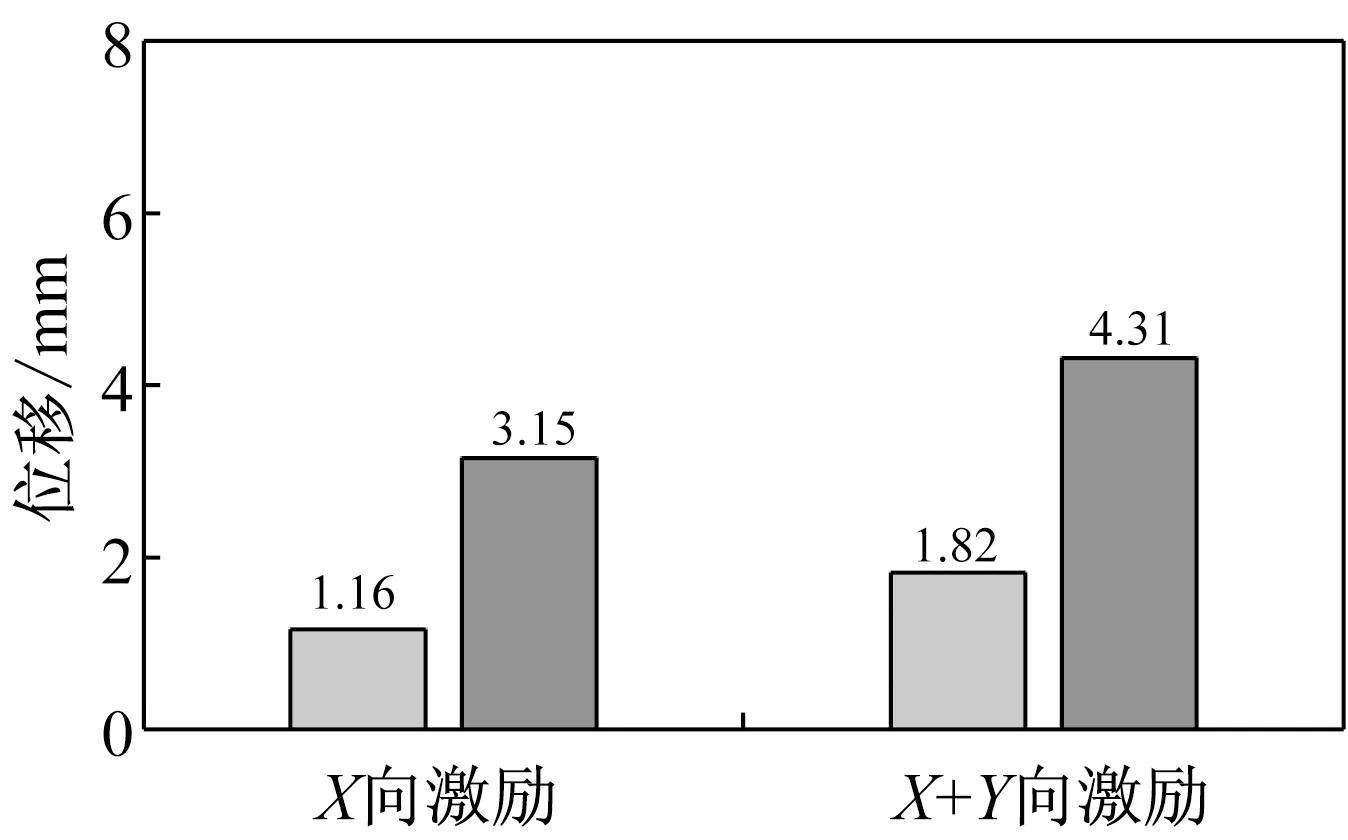
(c) 切向位移

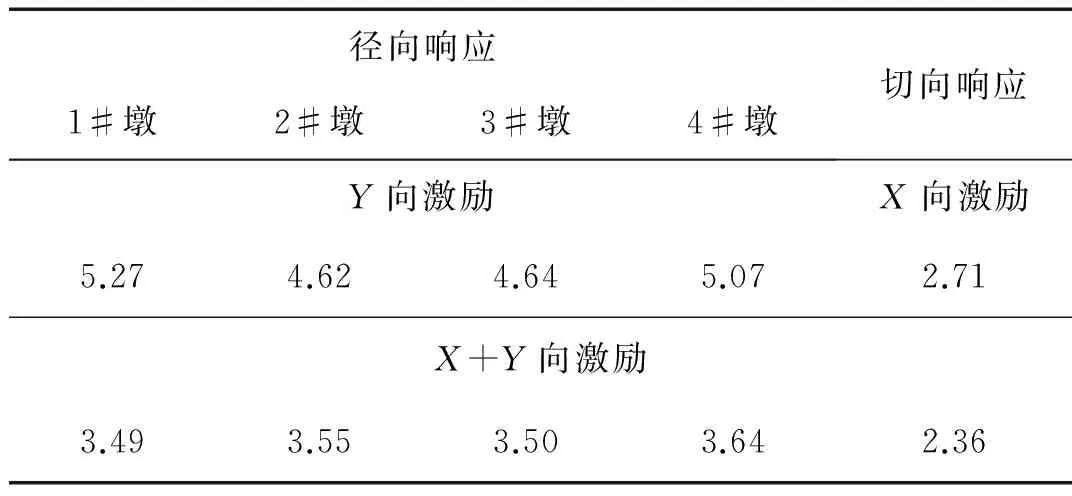
表5 近断层和远场地震作用下结构位移响应放大系数AFNTab.5 AFN of bent relative displacements under far-field and near-field ground motions

以上这些结果表明：①近断层地震动所包含的速度大脉冲会显著放大桥梁结构的响应;②放大作用会对刚度较大的结构或者结构的某一方向更为显著；③由于平面内的弯曲会使曲线桥的水平刚度大于同种类型的直线桥，因此可以推断出曲线桥对近断层效应更为敏感。

4.2 地震动空间效应

与一致激励相比较，可以看出当考虑行波效应时，各桥墩的相对位移都有了比较明显的增加(如图7所示)。在近断层地震动单向和双向激励下桥墩径向位移的放大系数的最大值分别为1.99和2.62，桥墩切向位移的放大系数分别为1.83和1.50。在远场地震单向和双向激励下桥墩径向位移的放大系数的最大值分别为2.52和1.49，桥墩切向位移的放大系数分别为1.45和0.89(如表6所示)。从上面的结果可以看出:①由行波效应引起的非一致激励会使桥墩的位移响应产生较为明显的作用;②不考虑行波效应可能会错误地估计结构的响应，特别是靠近断层区域的桥梁结构。因此在对大跨度曲线刚构桥进行抗震设计时有必要考虑地震动的行波效应。

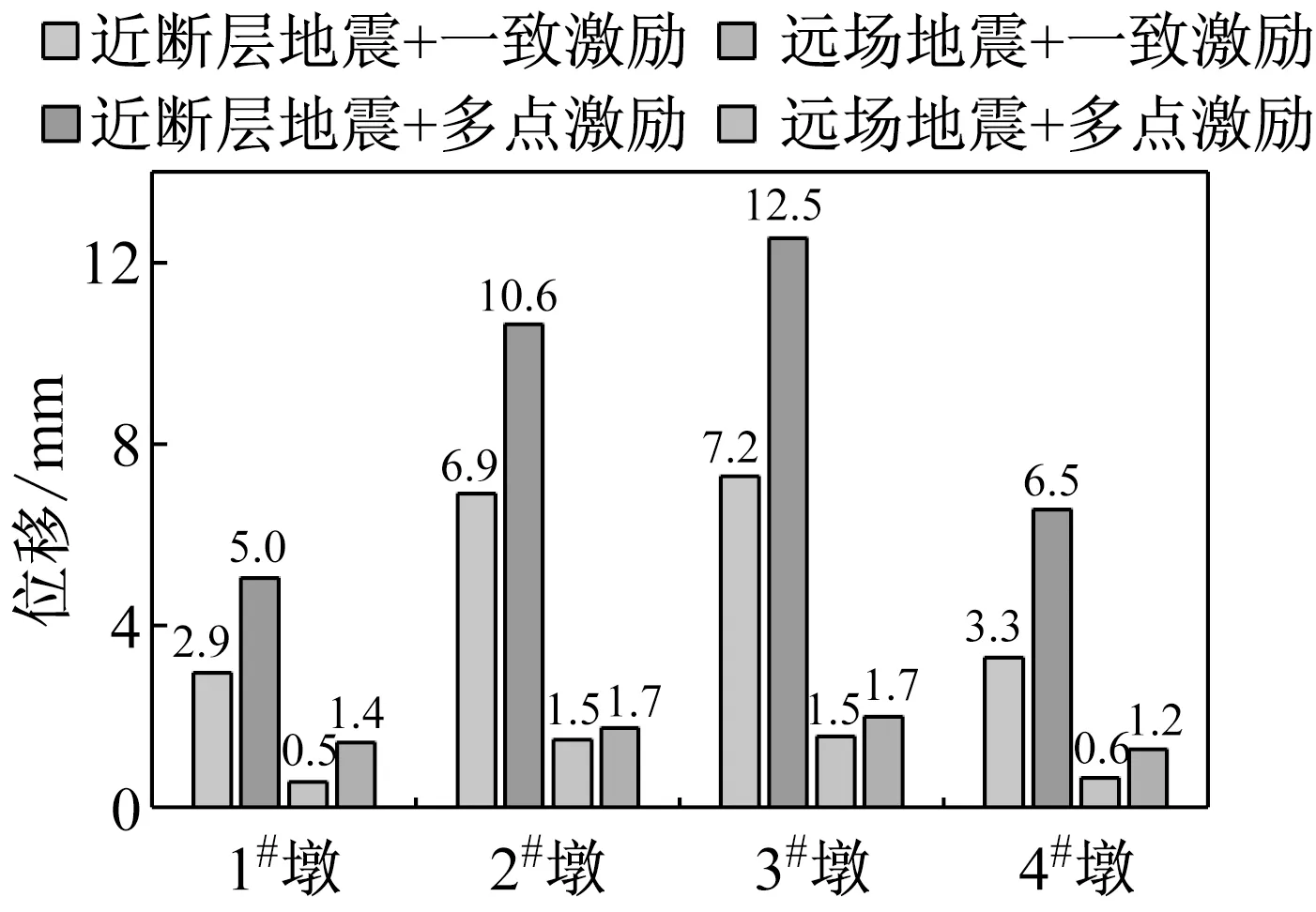
(a) Y向激励下的径向位移

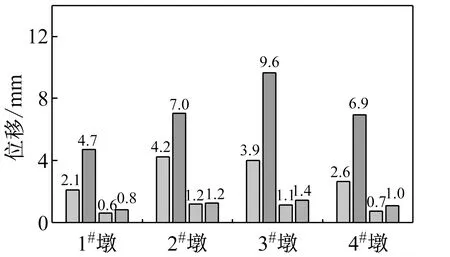
(b) X+Y项激励下的径向位移

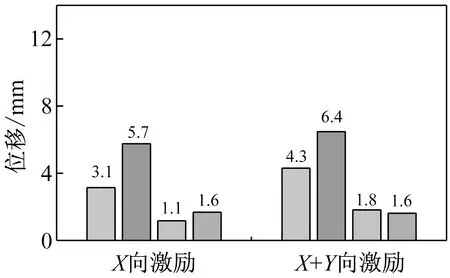
(c) 切向位移

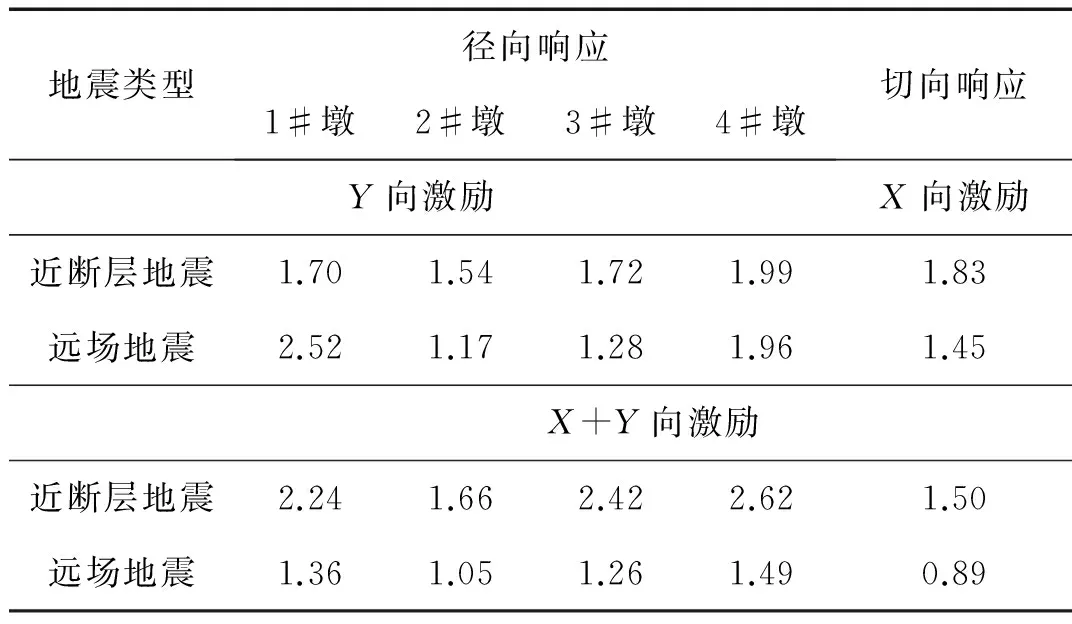
表6 一致和多点地震激励下结构位移响应放大系数AFWTab.6 AFW of bent relative displacements under synchronous and asynchronous excitations

从图7可以看出在一致激励作用下，处于对称位置的桥墩(1#墩和4#墩、2#墩和3#墩)的径向相对位移大小基本相同，而在多点激励下4#桥墩和3#桥墩的径向相对位移要分别大于1#桥墩和2#桥墩，从而使近断层地震动对3#桥墩和4#桥墩的放大作用要更为明显一些。产生这种现象的原因主要是因为一致激励作为对称荷载主要会激发结构的2阶模态(横向对称)，而多点激励作为非对称荷载不但会激发结构的2阶模态，还会激发结构的3阶模态(横向反对称)，如图5(b)所示，在对称模态和反对称模态共同影响下，处于对称位置的桥墩出现了不同的径向相对位移，并且导致地震对边墩的放大作用要明显于中墩，LI等[27]在曲线连续梁桥的振动台试验中也得到了类似的结论。

此外，以往针对直线桥的研究[28-29]也表明多点激励会激发结构的高阶反对称模态，从而对各桥墩产生不同的影响。但需要注意的是，对于对称布置的直线桥，多点激励一般会使处于对称轴一侧的中墩和边墩的径向位移减小，而放大另一侧中墩和边墩的径向位移。对于对称布置的曲线桥，本试验以及以往研究[27]均表明所有桥墩的径向位移在非一致激励下均会增大，只是地震对对称轴两侧桥墩的放大作用不同。产生这种现象的原因可以归结为曲线桥的几何不规则性，由于在平面内弯曲，曲线桥的横向刚度要大于相同类型的直线桥，从而使直线桥的高阶反对称模态更容易被激发，因此高阶反对称模态对直线桥的影响就更为明显。从上面的现象可以得出：①曲率半径会导致多点激励对同一类型的曲线桥和直线桥产生不同的放大作用;②曲线桥在同样的地震作用下会产生更严重的破坏，特别是靠近断层附近的曲线桥。因此建议在对曲线桥进行抗震设计时不但要考虑近断层效应，还应考虑行波效应带来的影响。

5 结 论

基于同一地震中来自两个不同测点的近断层地震动记录和远场地震动记录，本文设计制作了缩尺比为1/40的5跨曲线刚构桥，并通过振动台试验对比研究了近断层效应和行波效应对其抗震性能的影响。可以得出如下结论：

(1) 相对于远场地震，近断层地震动会对曲线刚构桥的动力响应产生显著影响，并且行波效应会进一步提升近断层地震动对结构动力响应的影响。在抗震设计中不考虑这些因素的影响，可能会严重低估结构的动力响应。

(2) 近断层效应的放大作用对刚度较大的结构或者结构的某一方向更为显著。由于曲率半径会增大曲线桥在水平方向上的刚度，因此在相同的近断层地震动作用下，曲线桥比直线桥更容易破坏，建议在抗震设计中要特别注意处于断层附近的曲线桥结构。

(3) 行波效应对结构响应的影响主要取决于多点激励所激发的高阶反对称模态。相对于直线桥，曲率半径会导致行波效应对曲线桥产生不同的影响，使其在地震作用下更容易破坏。

(4) 在本次试验中，没有考虑场地效应以及不同脉冲周期的近断层地震动对结构响应的影响，这些因素将在后续研究中基于大量数值模拟的参数分析进一步深入研究。

[1] 王辉，刘杰，申旭辉，等.断层分布及几何形态对川西及邻区应变分配的影响[J].中国科学:地球科学, 2010(4): 458-472.

WANG Hui, LIU Jie, SHEN Xuhui, et al.Influence of fault geometry and fault interaction on strain partitioning within western Sichuan and its adjacent region[J].Science China: Earth Science, 2010(4): 458-472.

[2] HAN Q, DU X, LIU J, et al.Seismic damage of highway bridges during the 2008 Wenchuan earthquake[J].Earthquake Engineering and Engineering Vibration, 2009, 8(2): 263-273.

[3] 刘启方，袁一凡，金星，等.近断层地震动的基本特征[J].地震工程与工程振动, 2006(1): 1-10.

LIU Qifang, YUAN Yifan, JIN Xing, et al.Basic characteristics of near-fault ground motion[J].Earthquake Engineering and Engineering Vibration, 2006(1): 1-10.

[4] HOUSNER G W, HUDSON D E.The port hueneme earthquake of march 18, 1957[J].Bulletin of the Seismological Society of America, 1958, 48: 163-168.

[5] BERTERO V V, MAHIN S A, HERRERA R A.A seismic design implications of near-fault san-fernando earthquake records[J].Earthquake Engineering & Structural Dynamics, 1978, 6(1): 31-42.

[6] KRAWINKLER H, ALAVI B, ZAREIAN F.Impact of near-fault pulses on engineering design[M].NATO Science Series IV-Earth and Environmental Sciences, Gulkan P, Anderson J G, 2005: 58, 83-106.

[7] HALL J F, HEATON T H, HALLING M W, et al.Near-source ground motion and its effects on flexible buildings[J].Erathquake Spectra, 1995, 11(4): 569-605.

[8] BRAY J D, RODRIGUEZ-MAREK A.Characterization of forward-directivity ground motions in the near-fault region[J].Soil Dynamics and Earthquake Engineering, 2004, 24(11): 815-828.

[9] CHOPRA A K, CHINTANAPAKDEE C.Comparing response of SDF systems to near-fault and far-fault earthquake motions in the context of spectral regions[J].Earthquake Engineering & Structural Dynamics, 2001, 30(12): 1769-1789.

[10] MOLLAIOLI F, BRUNO S, DECANINI L D, et al.Characterization of the dynamic response of structures to damaging pulse-type near-fault ground motions[J].Meccanica, 2006, 41(1): 23-46.

[11] JALALI R S, BAHARI JOKANDAN M, TRIFUNAC M D.Earthquake response of a three-span, simply supported bridge to near-field pulse and permanent-displacement step[J].Soil Dynamics and Earthquake Engineering, 2012, 43: 380-397.

[12] 李宁，李忠献，李杨.近断层地震动作用下桥梁结构易损性曲面分析[J].地震工程与工程振动，2014,34(增刊1):307-312.

LI Ning, LI Zhongxian, LI Yang.Seismic fragile surface analysis of reinforced concrete bridges subjected to near-fault ground motions[J].Earthquake Engineering and Engineering Dynamics, 2014,34(Supl):307-312.

[13] 翟长海，张林春，李爽，等.近场地震动对大跨刚构桥影响的分析[J].防灾减灾工程学报, 2010(增刊1): 143-147.

ZHAI Changhai, ZHANG Linchun, LI Shuang, et al.Effect of near-fault ground motions on the seismic responses of long span rigid bridge[J].Journal of Disaster Prevention and Mitigation Engineering, 2010(Supl): 143-147.

[14] ISMAIL M, CASAS J R, RODELLAR J.Near-fault isolation of cable-stayed bridges using RNC isolator[J].Engineering Structures, 2013, 56: 327-342.

[15] KARALAR M, PADGETT J E, DICLELI M.Parametric analysis of optimum isolator properties for bridges susceptible to near-fault ground motions[J].Engineering Structures, 2012, 40: 276-287.

[16] 石岩，王东升，孙治国.近断层地震动下减隔震桥梁地震反应分析[J].桥梁建设, 2014, 44(3): 19-24.

SHI Yan, WANG Dongsheng, SUN Zhiguo.Analysis of seismic response of seismically mitigated and isolated bridge subjected to near-fault ground motion[J].Bridge Construction, 2014, 44(3): 19-24.

[17] 王东升，冯启民，翟桐.近断层地震动作用下钢筋混凝土桥墩的抗震性能[J].地震工程与工程振动, 2003, 23(1): 95-102.

WANG Dongsheng, FENG Qimin, ZHAI Tong.Performance of reinforced concrete bridge piers subjected to near-fault ground motions[J].Earthquake Engineering and Engineering Vibration, 2003, 23(1): 95-102.

[18] CHOUW N, HAO H.Significance of SSI and nonuniform near-fault ground motions in bridge response I: Effect on response with conventional expansion joint[J].Engineering Structures, 2008, 30(1): 141-153.

[19] GOEL R K, CHOPRA A K.Role of shear keys in seismic behavior of bridges crossing fault-rupture zones[J].Journal of Bridge Engineering, 2008, 13(4): 398-408.

[20] PHAN V, SAIIDI M S, ANDERSON J, et al.Near-fault ground motion effects on reinforced concrete bridge columns[J].Journal of Structure Engineering, 2007, 133(7): 982-989.

[21] SAIIDI M S, VOSOOGHI A, CHOI H, et al.Shake table studies and analysis of a Two-Span RC bridge model subjected to a fault rupture[J].Journal of Bridge Engineering, 2014, 19(A40140038SI).

[22] 王天稳.土木工程结构试验[M].武汉: 武汉理工大学出版社, 2006.

[23] PEER.Technical report for the PEER ground motion database web application[R].Pacific Earthquake Engineering Research Center, 2010.

[24] BAKER J W.Quantitative classification of Near-Fault ground motions using wavelet analysis[J].Bulletin of the Seismological Society of America, 2007, 97(5): 1486-1501.

[25] MAYES R L, SHAW A.The effects of near fault ground motions on bridge columns[C].Burlingame, California: 1997.

[26] LIAO W I, LOH C H, WAN S.Dynamic responses of bridges subjected to near fault ground motions[J].Journal of the Chinese Institute of Engineers, 2000, 23(4): 455-464.

[27] LI X, ZHANG D, YAN W, et al.Shake-Table test for a typical curved bridge: Wave passage and local site effects[J].Journal of Bridge Engineering, 2015, 20(040140612).

[28] TZANETOS N, ELNASHAI A S, HAMDAN F H, et al.Inelastic dynamic response of RC bridges subjected to spatial non-synchronous earthquake motion[J].Advances in Structural Engineering, 2000, 3(3): 191-213.

[29] MONTI G, NUTI C, PINTO P E.Nonlinear response of bridges under multisupport excitation[J].Journal of Structural Engineering, 1996, 122(10): 1147-1159.

Shaking table tests for a long-span curved rigid bridge under near-fault ground motions

LI Xi, JIA Hongyu, LI Qian

(1.School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;2.Key Laboratory of High speed Railway Engineering Ministry of Education, Southwest Jiaotong University, Chedngdu 610031, China)

To study the effects of near-fault ground motions on a long-span curved rigid bridge, an actual curved rigid bridge based on a scale of 1/40 model was employed to conduct shaking table tests.The typical near-fault and far-field ground motions recorded under the same earthquake were selected as the ground motion input, and then comparative tests on a multi-shaking table array system were carried out.During tests, the structure was subjected to synchronous and traveling wave excitations taken as longitudinal and transverse inputs, and the combination of transverse and longitudinal inputs, respectively.The results showed that the velocity pulse contained in near-fault ground motions has a significant influence on the dynamic response of the curved rigid bridge and the structural response amplification effect can be further elevated by traveling wave effect; near-fault effect is more obvious for the structure with a larger stiffness or a certain direction of the structure, whereas the influence of traveling wave effect on the structure is dependent primarily upon higher order asymmetric modes induced by mult-point excitations; compared with a straight line bridge, both near-fault effect and traveling wave effect cause more harmful influence on the dynamic response of the curved bridge due to a larger stiffness in horizontal direction caused by curvature radius; therefore, the curved bridge may be damaged more seriously than a straight bridges may under the same earthquake in near-fault zone.It was suggested that special attentions should be received for a curved rigid bridge close to fault zones.

near-fault ground motions; curved rigid bridge; shaking table test; dynamic response

国家自然基金项目(51508473)；中央高校基本科研业务费专项资金科技创新项目(10101B10096037)

2016-05-11 修改稿收到日期：2016-07-13

李晰 男，博士，讲师，1984年2月生

贾宏宇 男，博士，讲师，1981年10月生

TU317+.1; TU352.1

A

10.13465/j.cnki.jvs.2017.05.032