基于JADE-ICA的滚动轴承多故障信号盲源分离

席剑辉, 崔健驰, 蒋丽英

(沈阳航空航天大学 自动化学院,沈阳 110036)

基于JADE-ICA的滚动轴承多故障信号盲源分离

席剑辉, 崔健驰, 蒋丽英

(沈阳航空航天大学 自动化学院,沈阳 110036)

研究一种基于源信号高阶统计信息的矩阵联合近似对角化独立元分析(JADE-ICA)方法，并将其应用于滚动轴承故障声发射(AE)信号的盲源分离。滚动轴承的声发射源信号一般具有衰减性和准周期性，多组信号间还具有时差性，信号被多个传感器接收。通过最大程度的联合近似对角化，可以使源信号与分离信号有效的一一对应，克服非线性和时差的影响；通过高阶统计的高斯噪声不敏感性可以有效抑制随机观测噪声对分离结果的影响。选用相关系数、二次残差、性能指数和频谱特征构成系列时频域评价指标对分离结果进行较为全面的验证。仿真结果证明了该方法的可行性和有效性。

JADE；滚动轴承；故障诊断；声发射

旋转机械的故障有30%由轴承故障引起[1]，轴承状态对机器的工作状况影响极大。因此，对轴承进行工况检测与故障诊断是非常必要的。声发射检测是一种动态无损检测方法，声发射信号来自缺陷本身。轴承在运转过程中，轴承内外圈滚道及滚动体上出现的点蚀、剥落、裂纹等疲劳损坏部位与其他部位之间的摩擦碰撞，将导致声发射信号的产生。因此可以利用轴承的声发射信号对轴承的安全性及运行状态进行长期监测[2]。何沿江等[3]采用独立分量分析(ICA)和支持向量机(SVM)结合进行滚动轴承故障诊断，利用ICA提取声发射信号的特征状态。杨黎明[4]提出将声发射检测应用于滚动轴承在线故障诊断，分析故障轴承的声发射信号特征以及声发射信号特征的表示方法。实际系统中，这种摩擦碰撞产生的声发射信号往往来自滚动轴承外圈、内圈和滚柱等不同部位多个损伤点，声发射传感器测取的声发射信号是多个激振源所激起的振动混叠，同时还包含了测量噪声。将声发射信号按照不同的激振源进行分离，是轴承状态监测与多故障诊断的关键步骤，也是难点。

传统独立成分分析(ICA)进行盲源分离只能适用于统计独立源，且易受噪声影响。高阶统计是一种现代信号处理方法，对高斯噪声不敏感，可以反映高阶相关的非线性关系[5]。矩阵联合近似对角化(Joint Approximate Diagonalization of Eigen-matrices，JADE)算法是由法国学者CARDOSO等[6]提出的，该算法利用高阶累积量将ICA问题转化为特征矩阵对角化问题。王权锋等[7]利用JADE算法分析金属矿地震数据，在降噪方面得到了很好的效果。陈恩利等[8]监测轴承外圈剥离单一故障和滚动体表面损伤单一故障下的振动信号，验证了JADE方法应用于故障检测的可行性。

本文研究针对滚动轴承多声发射源信号的JADE-ICA方法，实现轴承多故障源的分离；同时研究多种评价指标对分离后的信号进行分析与比较，以及时发现故障隐患，验证分离结果的有效性。

1 多故障带噪声信号的盲源分离

设m个声发射源信号s1，…，sm，被n个传感器测得的信号为x1，…，xn，信号源噪声为w1，…，wm(m≥n)则某一时刻t，测量信号是源信号的线性组合

xi=ai1(s1(t)+w1(t))+…+aim(sm(t)+wm(t))

(1)

式中:aij，i= 1，2,…，n，j=1，2,…，m是实系数。si在统计上彼此独立，称为隐变量，wi与si叠加。上式的矩阵形式为

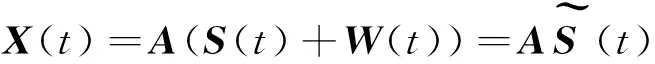
(2)

其中X(t)=[x1(t),…,xn(t)]T，S(t)=[s1(t),…,sm(t)]T，W(t)=[w1(t),…,wm(t)]T，A为混合矩阵。分离源信号就是找到分离矩阵U使

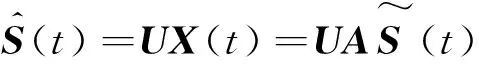
(3)

如果

UA=I

(4)

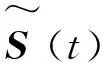
2 基于JADE的独立元分析

如果声发射源信号之间相互统计独立，则盲源分离的过程就是寻找观测的混合信号中独立元的过程。关键步骤是寻找混合矩阵A或者分离矩阵U。

2.1 基于四阶累积量的混合矩阵A估计

JADE算法是基于四阶累积量的一种算法，对于n个随机变量x1，…，xn，四阶累积量定义如下：

cum(xi,xj,xk,xl)=E[xixjxkxl]-E[xixj]E[xkxl]-

E[xixk]E[xjxl]-E[xixl]E[xjxk]

(5)

式中：i，j，k，l= 1，2,…，n。则对应四阶累积量矩阵的i行j列的元素可以表示为

(6)

式中:mkl为n×n阶任意权重矩阵M的第k，l元素。如果X中各变量均值为零，根据式(5)和(6)，X的累积量矩阵可以写成以下形式[9]：

(7)

式中：tr(·)表示矩阵的迹，RX是矩阵X的协方差矩阵。文献[9]中证明，当观测信号X变量之间统计独立时，该四阶累积量矩阵可以表示为

CX(M)=AΔ(M)AT

(8)

式中：λi为CX(M)的特征值，ai是A的列向量，i=1，…，n，A=[a1,2,…,an]。

取2个n×n阶矩阵M1和M2，根据式(8)，

CX(M1)=AΔ(M1)AT

CX(M2)=AΔ(M2)AT

(9)

Δ(M1)，Δ(M2)为对角矩阵。令

(10)

这里Δ=Δ(M1)Δ(M2)-1是一个对角矩阵。

由式(10)，可以得出

GA=AΔ

(11)

所以Δ的对角线元素可看成是G的特征值，A是G的特征向量，理论上求出G的特征向量也就相当于找到了混合矩阵A。

2.2 信号白化处理

上述讨论成立的条件是矩阵A可逆，且源信号为零均值，相互之间统计独立。因此实际情况中，必须首先对观测信号加入中心化和白化过程保证条件成立。中心化就是对观测的n个变量xi(t)，i= 1，2,…，n。用xi(t)-E[xi]来代替xi(t)，使得观测序列xi(t)变成零均值序列。白化是去除各分量之间的相关性，保证各分量之间统计独立。不失一般性，仍设中心化后的观测变量矩阵为X(t)=[x1(t),…,xn(t)]T，t= 1，…，N，N为观测点数，则其协方差矩阵为

(12)

V为酉矩阵，Σ为RX的特征值对角矩阵，则白化变换阵Q为

Q=Σ-1VT

(13)

白化后的信号为

Z(t)=QX(t)

(14)

其协方差矩阵为

RZ=E[ZZT]=Σ-1VTVΣ2VTVΣ-1=I

(15)

实现白化。令H=QA，则

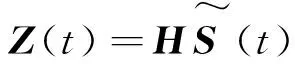
(16)

则2.1节基于X(t)求A的过程就转化为基于白化矩阵Z(t)求H的过程。

2.3 联合近似对角化

在实际计算中，由于数值计算误差和干扰噪声的存在，无法实现完全对角化，只能进行近似对角化。对任取的两个矩阵M1和M2不能保证一定找到最优的H，因此采用联合近似对角化方法。基于白化后信号Z(t)，取p个n×n阶任意矩阵M1，…，Mp，为达到精度要求，一般取p=n2。对每个Mi求Cz(Mi)(i=1，2,…，p)，找到一个酉矩阵H，使下面的式子达到最小

(17)

式中:off(·)定义为矩阵所有非对角元素的平方和。

混合信号独立元的估计为

(18)

3 基于JADE的多故障声发射信号盲源分离

声发射传感器通常布置在轴承座或机壳上，采集的信号经过传递，各信号之间的统计独立性易受传递时差、噪声等干扰，盲源分离时需要先进行白化处理。

3.1 基本步骤

步骤1 对每一路观测的故障信号数据进行中心化处理；

步骤2 利用式(12)～(14)对数据进行白化得到Z(t)，t=1，2,…，N。

步骤3 取p个权矩阵M1，…，Mp，根据式(7)计算Z(t)的四阶累积量矩阵组CZ(Mi)，i=1，2,…，p，一般可取p=n2。

步骤4 对步骤3中的矩阵组CZ(Mi)进行联合近似对角化，使优化目标函数(17)达到最小，从而得到酉矩阵H。

步骤5 计算分离矩阵U=HTQ。

步骤6 按照式(3)估计源信号。

步骤7 分离信号特征分析，进行故障诊断。

3.2 分离效果的评价指标

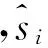
(19)

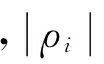
二次残差采用带幅值修正因子的计算公式[11-12]

(20)

VQM的值越小，分离效果越好。该值小于-23 dB时，分离效果较好。

由式(3)和式(4)，令Φ=UA，理想情况下应为单位阵。考虑ICA方法输出向量排列顺序的不确定性，Φ可以是一个每行每列有且只有一个1元素的矩阵，此时一个源信号对应一个分离信号，为有效分离。PI即为衡量实际Φ阵与上述一一对应要求差别的指标[12]。公式如下：

(21)

式中:hij为矩阵Φ的第(i，j)个元素。PI值越小分离效果越好。

此外，考虑旋转机械在运行过程中，由于疲劳损伤部位摩擦碰撞等产生的声发射或振动信号必然带有一定的周期特征。因此对旋转机械来说，频域特征如谐振频率等是体现分离信号有效性的一个关键因素[13]，需要纳入到分离效果的评价指标中。

4 仿真实例

4.1 仿真声发射源信号分离及其效果评价

为验证本文方法的正确性，模拟四组滚动轴承声发射源信号如式(21)所示，信号反映了滚动轴承声发射信号的周期性、衰减性及时差性。

s1=4sin(0.4πt)e-0.02t+ω1(t)

(22)

s3=4sin(πt)e-0.02t·1(t-40)+ω3(t)

s4=2sin(4.6πt)e-0.02t·1(t-60)+ω4(t)

式中：ωi(t)，i=1，2,…，4，为随机白噪声。将四组信号随机混合，分别采用FastICA方法和JADE-ICA方法对信号源分离，源信号如图1所示，FastICA分离信号如图2所示，JADE-ICA分离信号如图3所示。评价指标值如表1所示。

比较图2和图3，结合表1可以看出，非线性源信号受噪声、时差的影响，而且信号间可能具有一定相关性(s2和s3)，FastICA不能良好地区分时差带来的混叠。采用JADE-ICA方法，利用近似对角化过程和高阶累积量的抑噪性，可以获得更好的分离结果。时域的三个指标相关系数ρi更接近于1，二次残差VQM更小，性能指数PI更小。对JADE-ICA方法的分离信号做频谱分析，其谐振频率与源信号相同，较好地反映了源信号的频率特征。

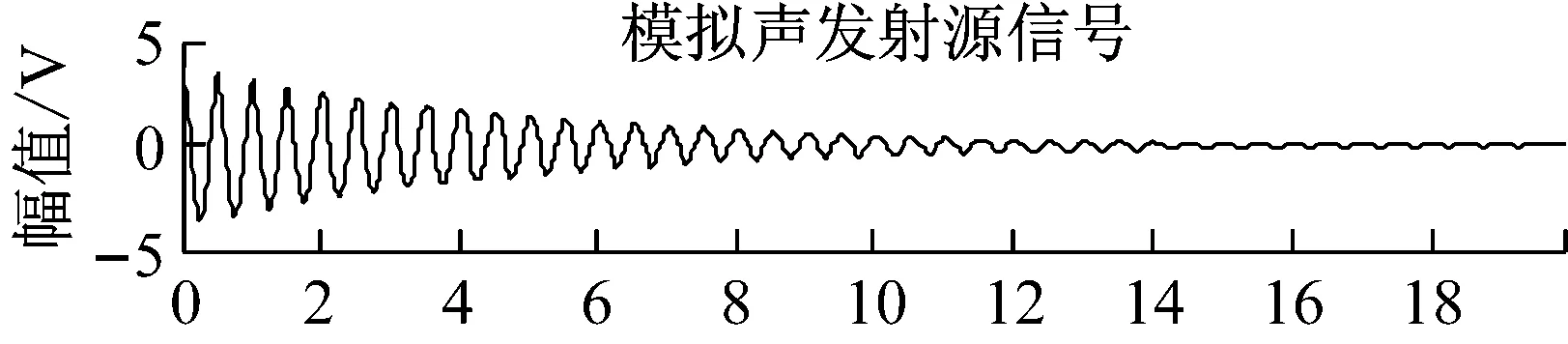
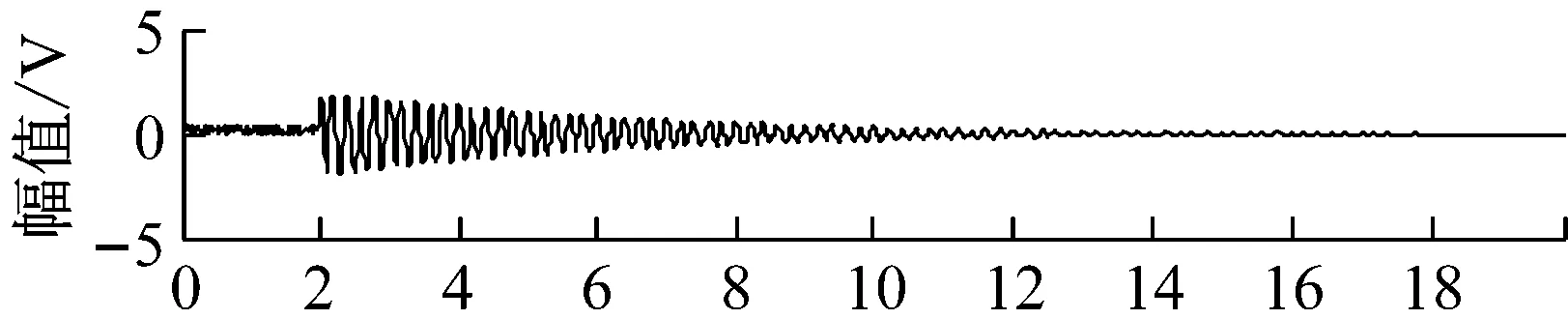
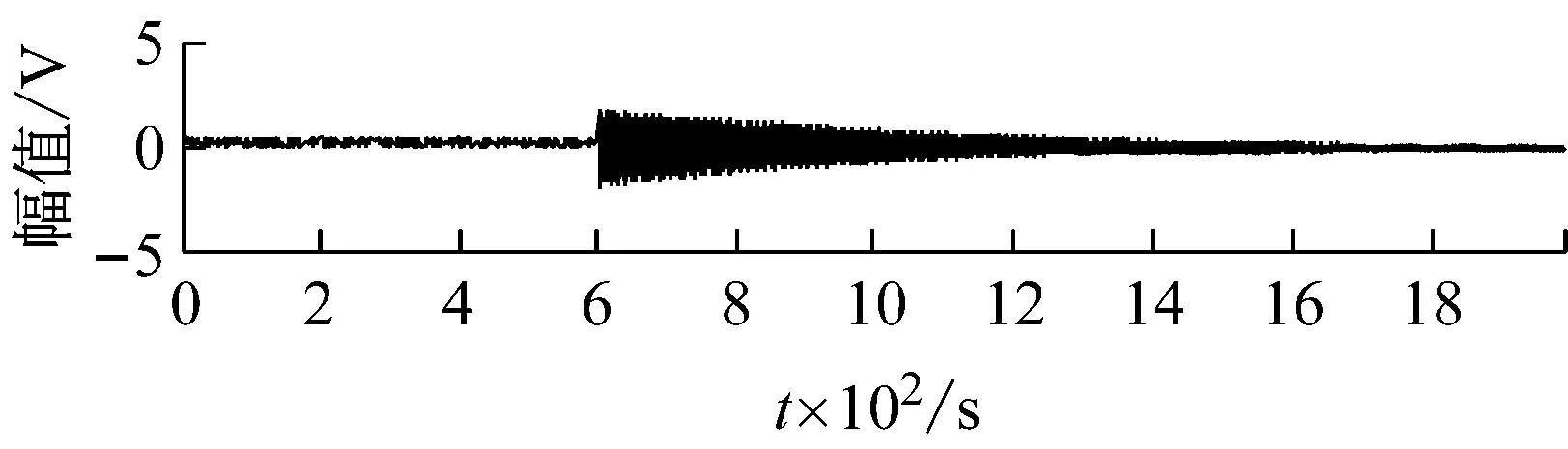
图1 4组模拟声发射源信号Fig.1 Four sets of simulated AE source signals

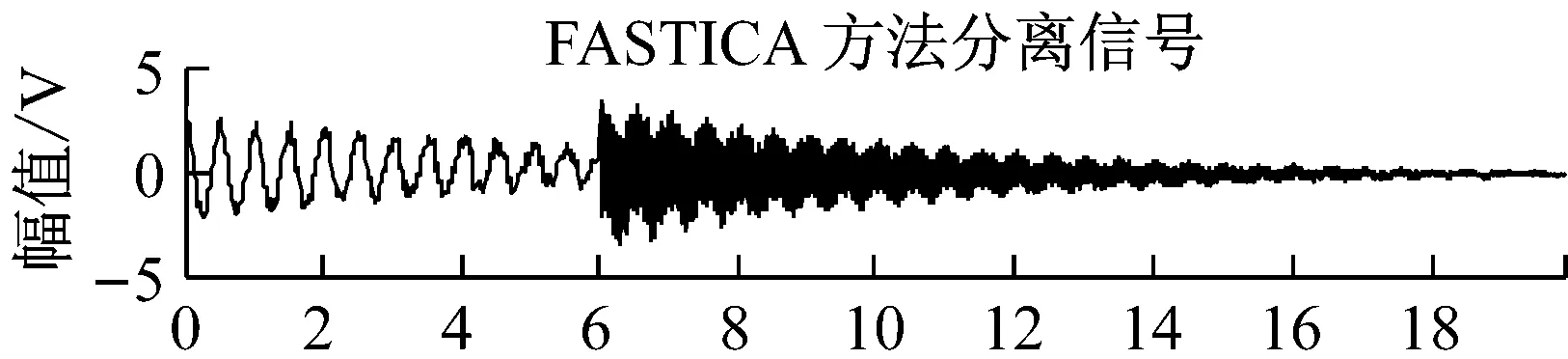
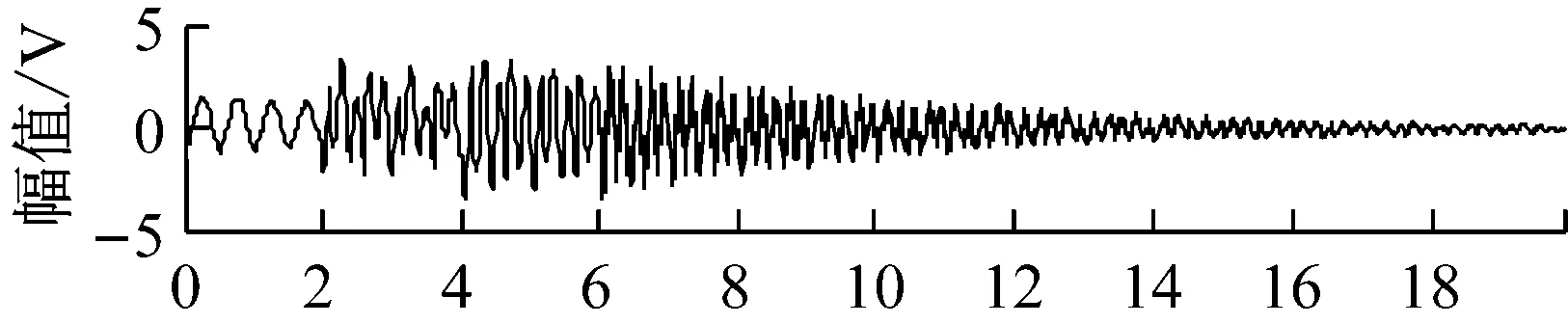
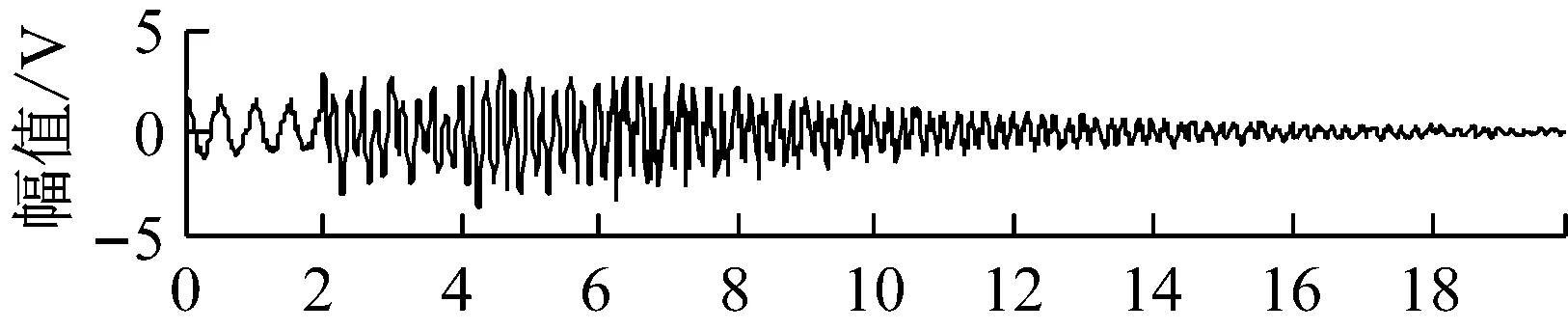
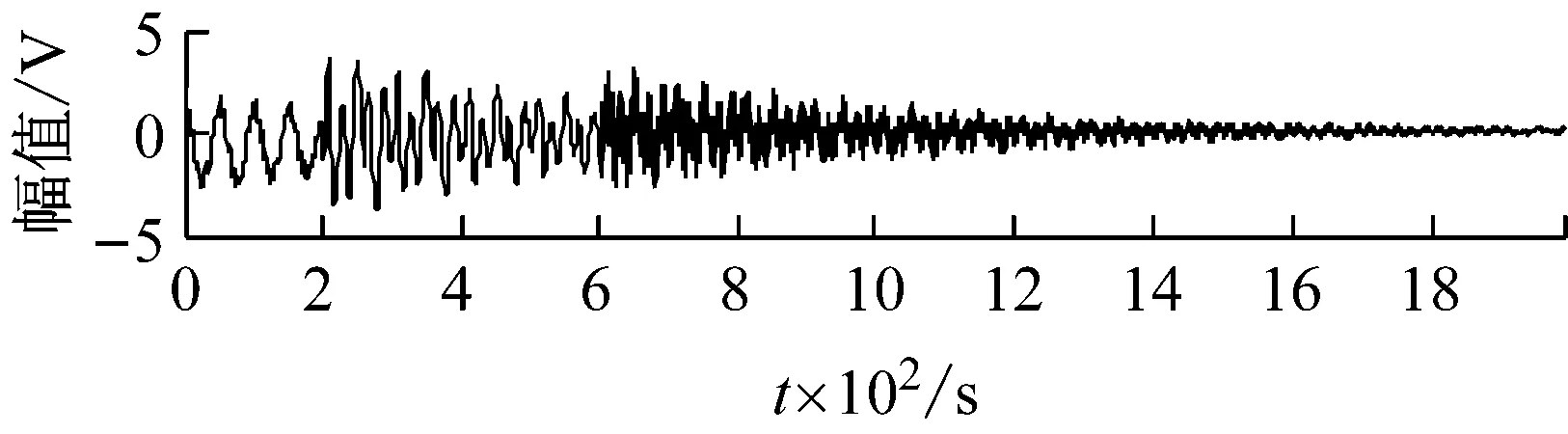
图2 FastICA方法的分离信号Fig.2 The separated signals by FastICA method

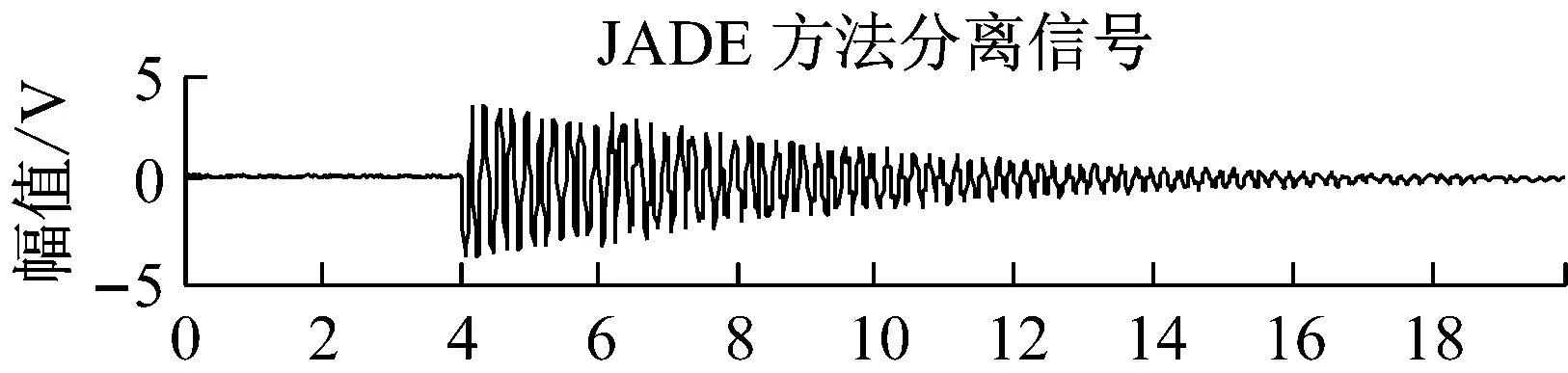
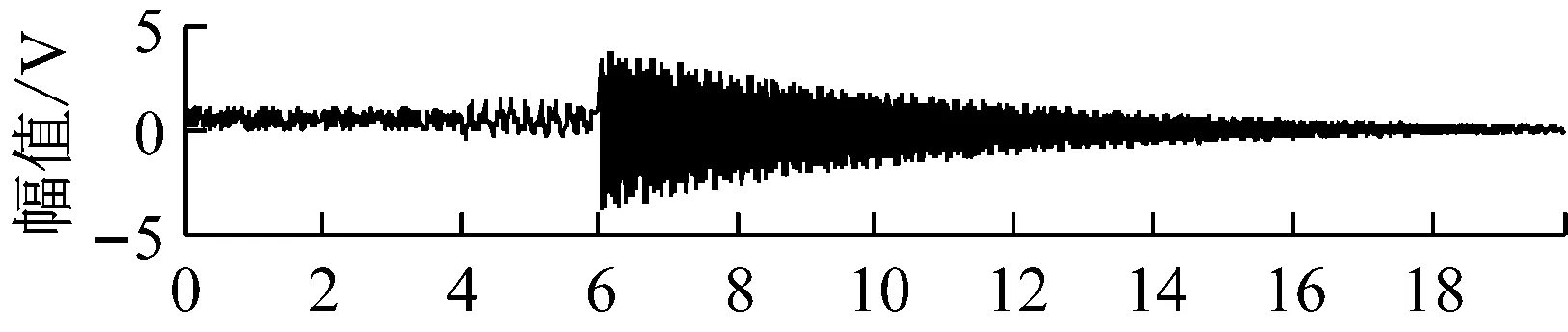
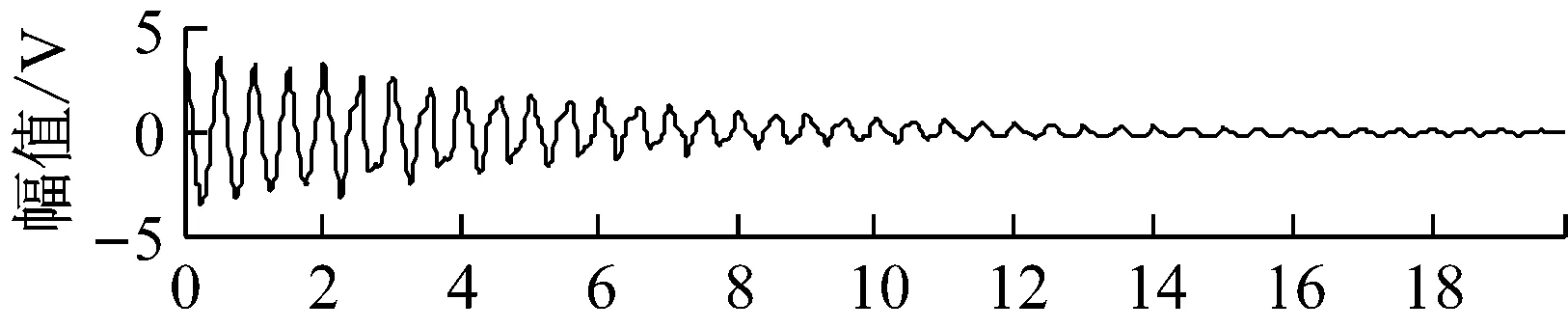
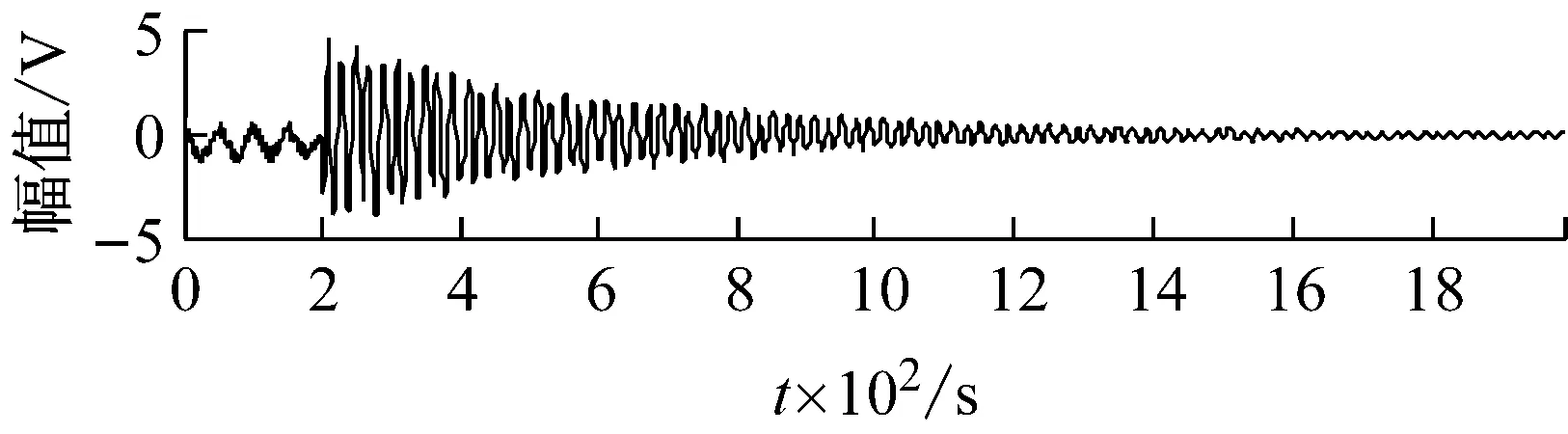
图3 JADE-ICA方法的分离信号Fig.3 The separated signals by JADE-ICA method

4.2 滚动轴承实测信号分离及其效果评价

实验采用型号为N205EM的圆柱滚子轴承，旋转机械故障模拟平台如图4所示。实验中通过对轴承的内、外圈和滚柱切割沟槽来模拟滚动轴承的局部损伤故障，缺陷宽度为1 mm。

表1 盲源分离评价指标比较

Tab.1 Evaluation indexes comparison of blind source separation

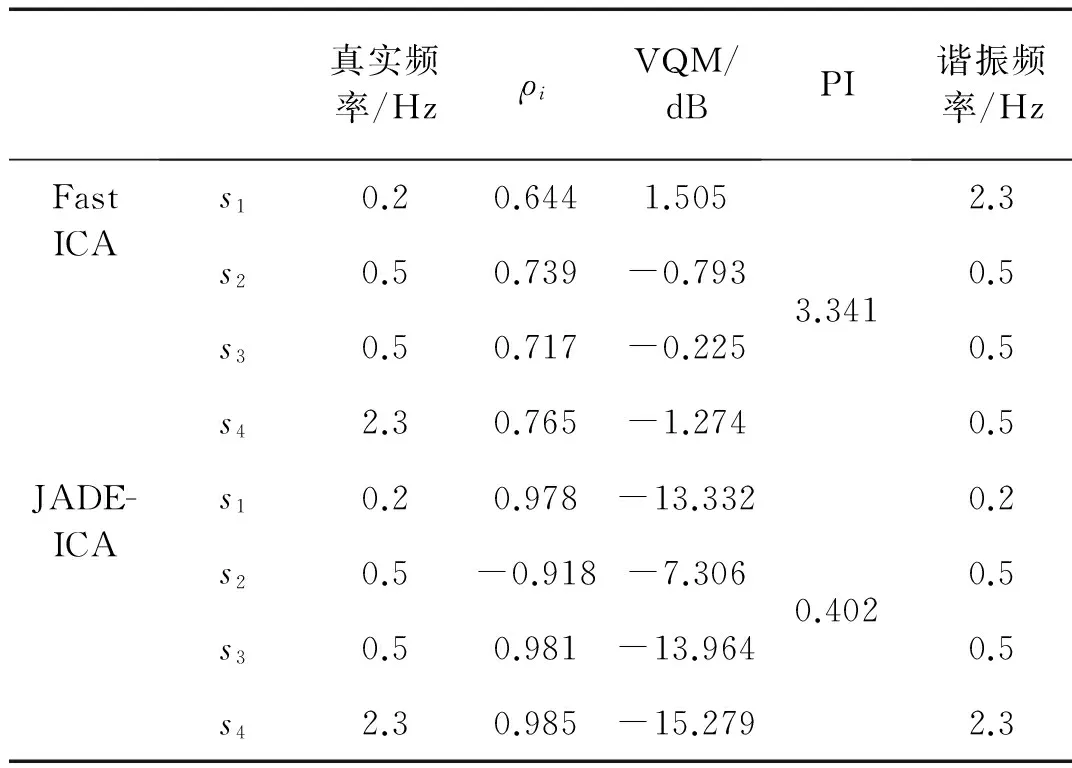
真实频率/HzρiVQM/dBPI谐振频率/HzFastICAs10.20.6441.505s20.50.739-0.793s30.50.717-0.225s42.30.765-1.2743.3412.30.50.50.5JADE-ICAs10.20.978-13.332s20.5-0.918-7.306s30.50.981-13.964s42.30.985-15.2790.4020.20.50.52.3

1.三相交流变频电机; 2.传动轴支座; 3.轴承座; 4.旋转轴

采用声华SAEU2S数字声发射测试系统进行信号的采集工作。传感器采用SR150M型，固定在如图轴承座3的正上方，前置放大器放大倍数为40 dB。实验中电机转速为900 r/min，采样频率为1 000 kHz。

(1) 模拟多故障声发射信号仿真

为方便分离结果与源信号的比较，验证方法有效性。先分别采集轴承外圈故障、内圈故障和滚柱故障3种运行状态下的声发射信号作为源信号，如图5所示。对三种源信号随机混合，模拟多故障情况。为使结果更可靠，多次重复随机混合过程并进行分离仿真，计算时频域评价指标，取多次仿真的平均值作为最终的评价指标。

任选一组随机混合信号如图6所示。对混合故障信号分别采用FastICA算法和JADE算法进行分离，该组信号的分离结果如图7和图8所示。

重复以上混合和分离过程，10次仿真的平均指标如表2所示。同理计算三种时域指标如表2所示，可以看出，JADE的联合近似对角化过程对非线性声发射源信号具有良好的分离效果，三种指标都更接近于理想值。因为源信号频率未知，这里给出源信号和任选一组分离信号的频谱如图9～图11所示，比较可以看出源信号与分离信号的能量集中频带基本一致。外圈故障源信号与分离信号的谐振频率有一定误差，源信号为14.9 Hz，分离信号为18.3 Hz，但分离信号在14.9 Hz处也有一个频谱峰值，说明该频率特征也包含在分离信号中。通过频谱分析可以进行故障源的判断。

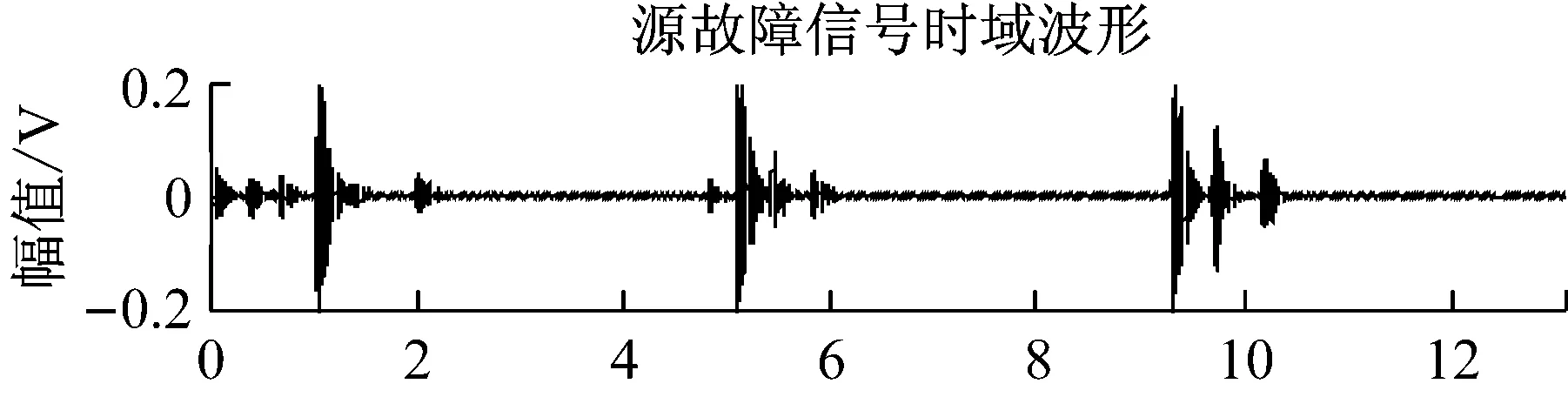
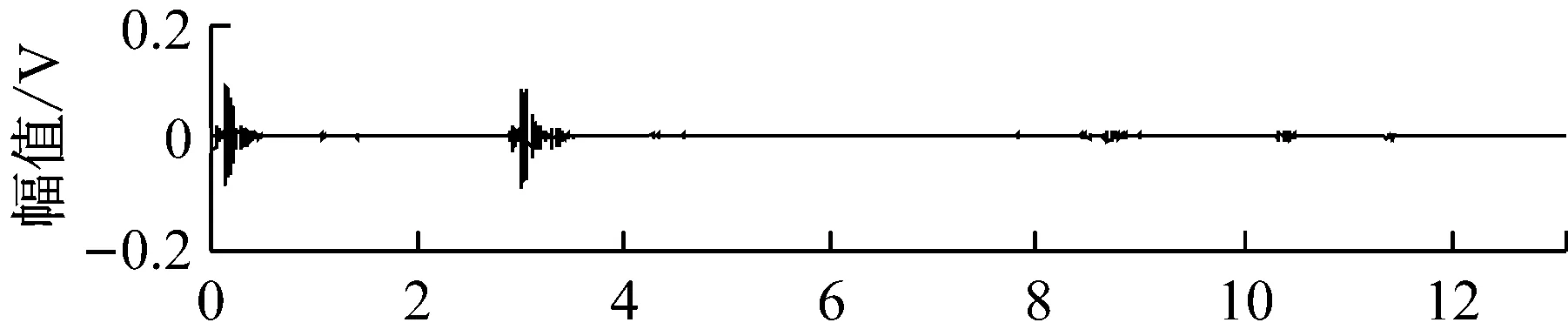
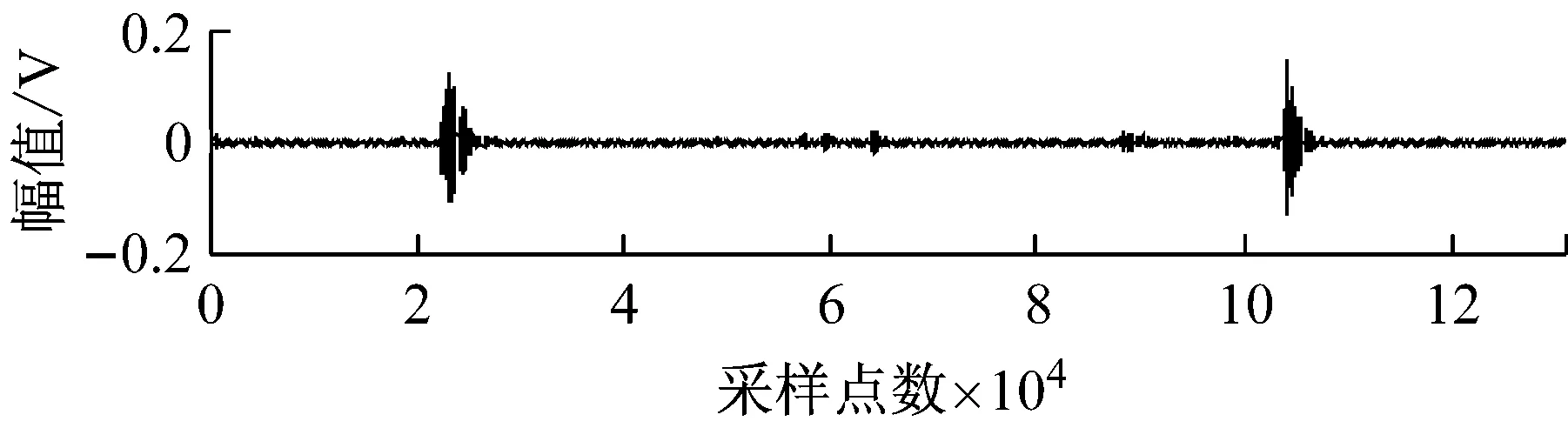
图5 故障信号波形Fig.5 The waveforms of the fault signals

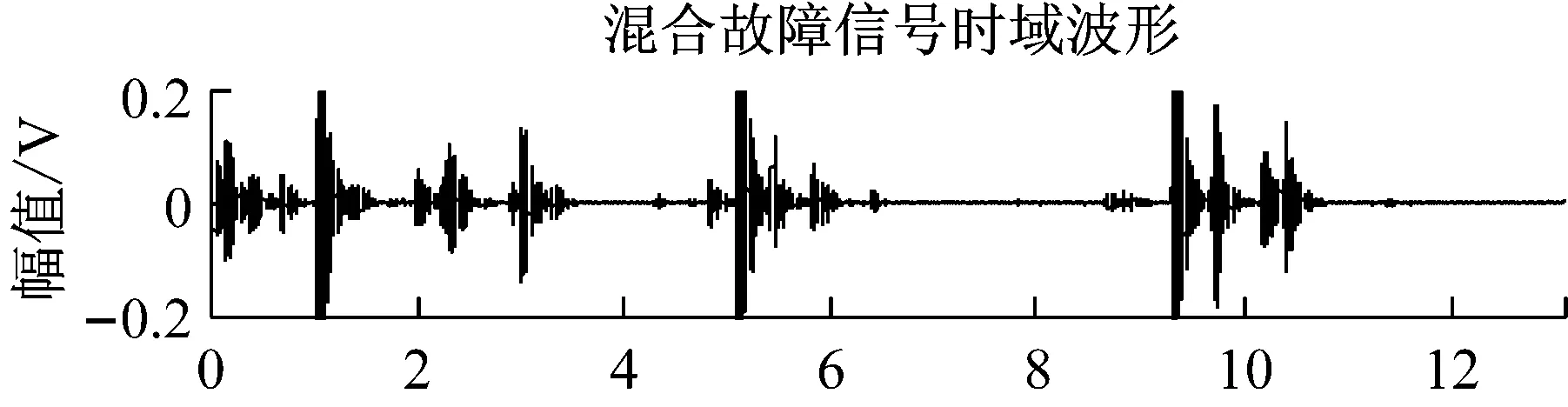
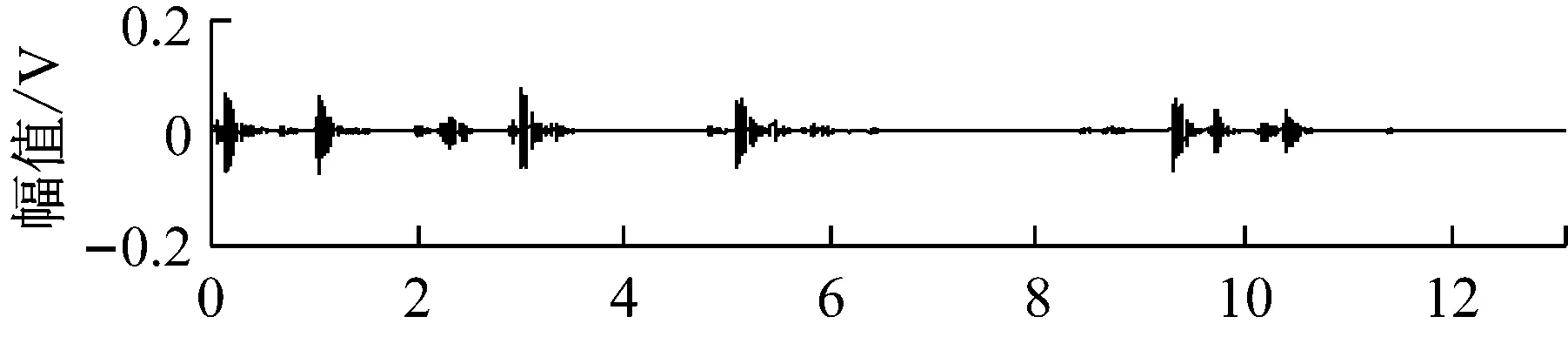
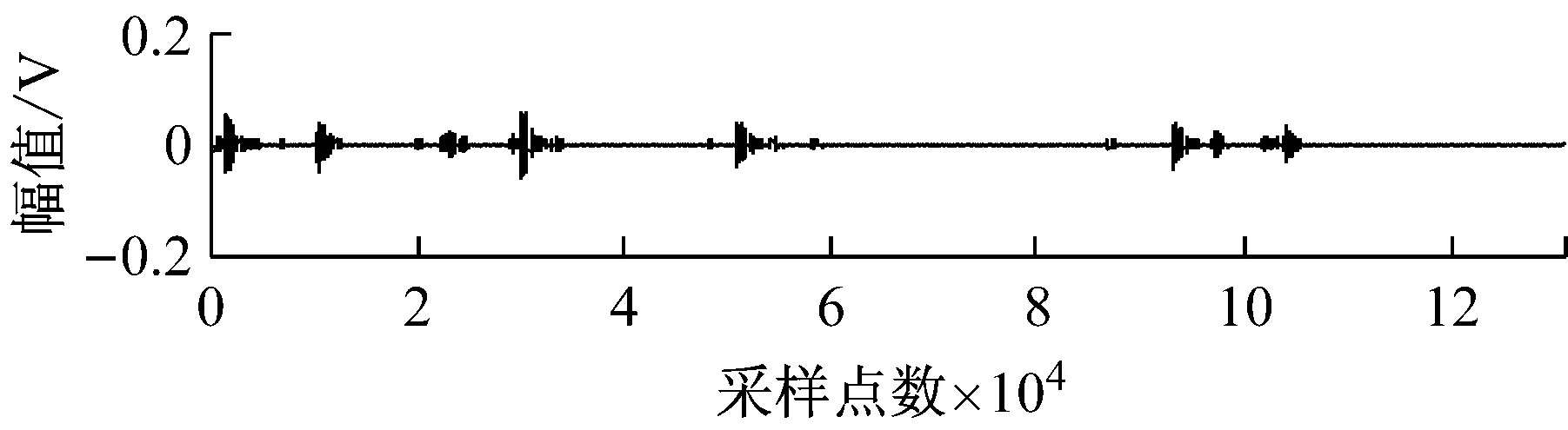
图6 随机混合的故障信号波形Fig.6 The waveforms of the randomly mixed fault signals

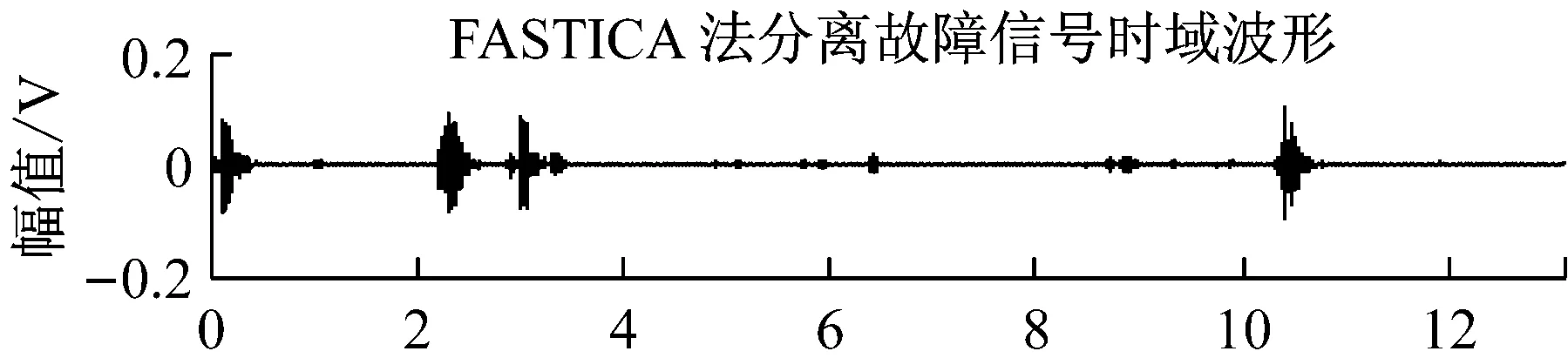
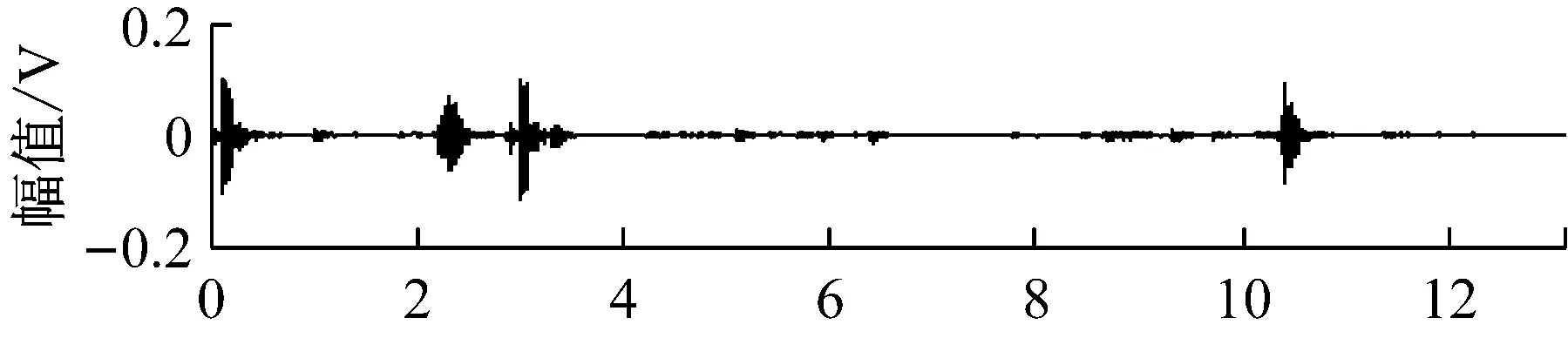
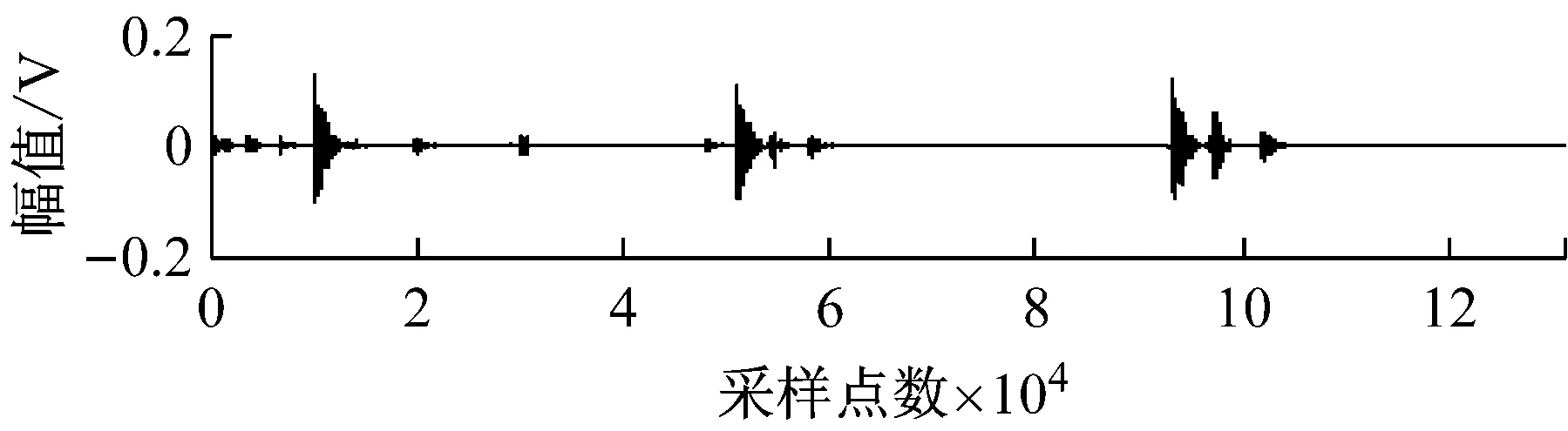
图7 FASTICA法分离的故障信号波形Fig.7 The waveforms of the separated fault signals by FastICA

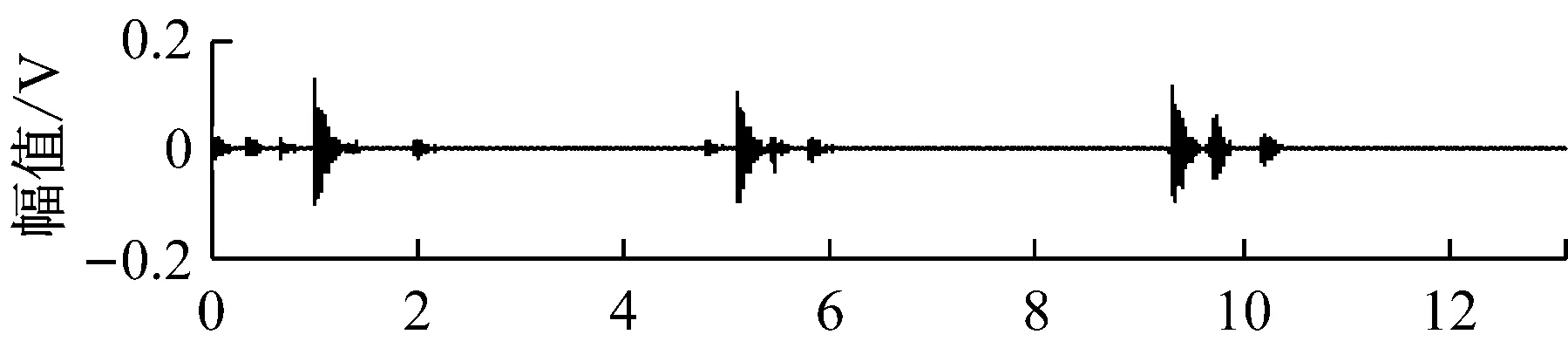
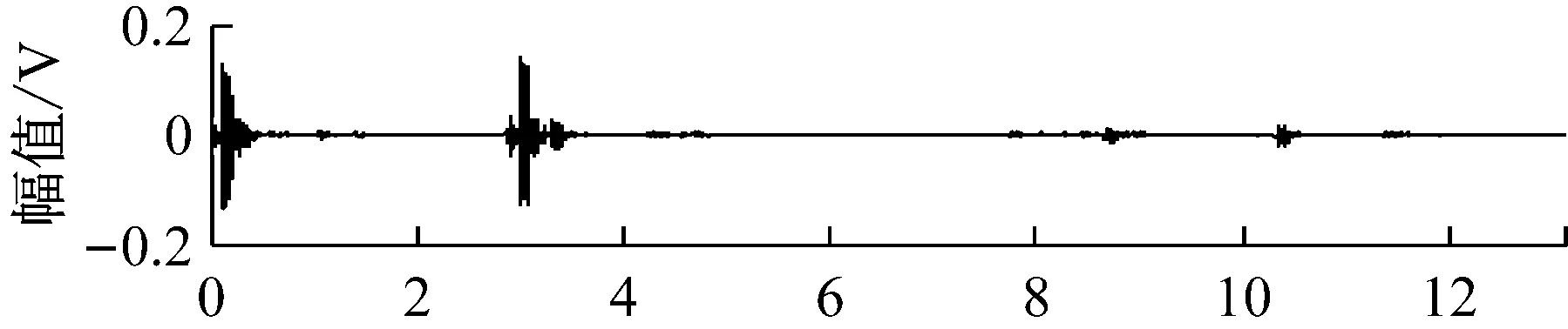
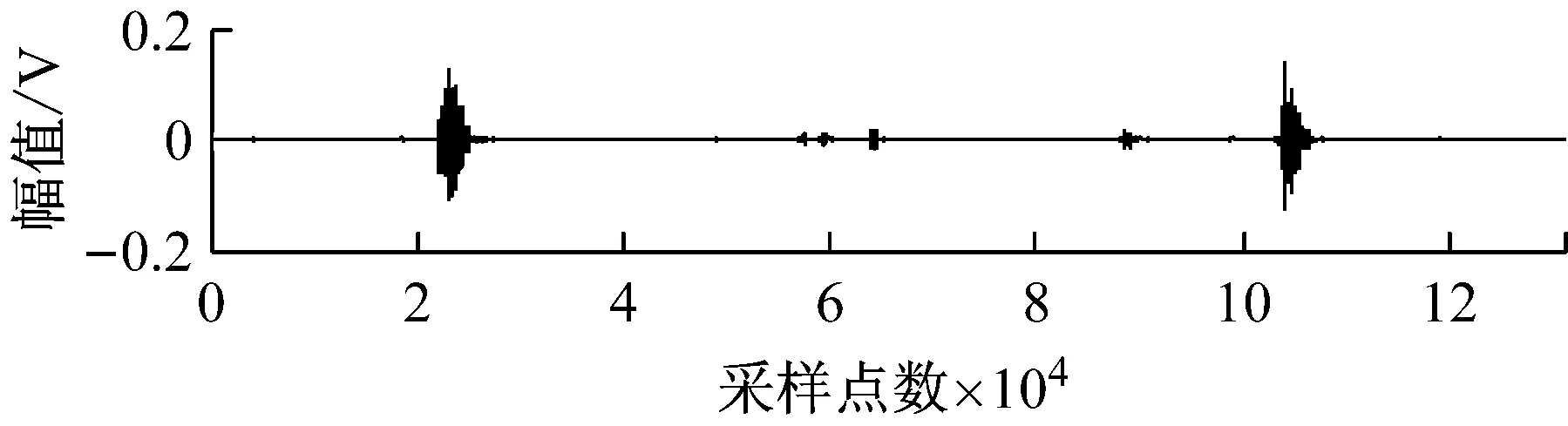
图8 JADE法分离信号时域波形Fig.8 The waveforms of the separated fault signals by JADE-ICA

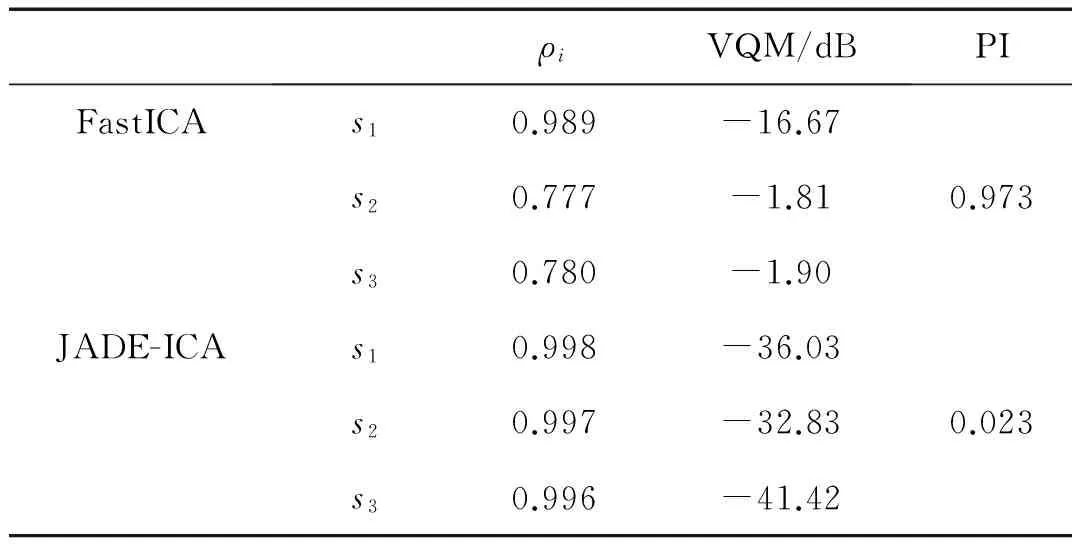
表2 声发射源分离评价指标比较Tab.2 Evaluation indexes comparison of AE source separation

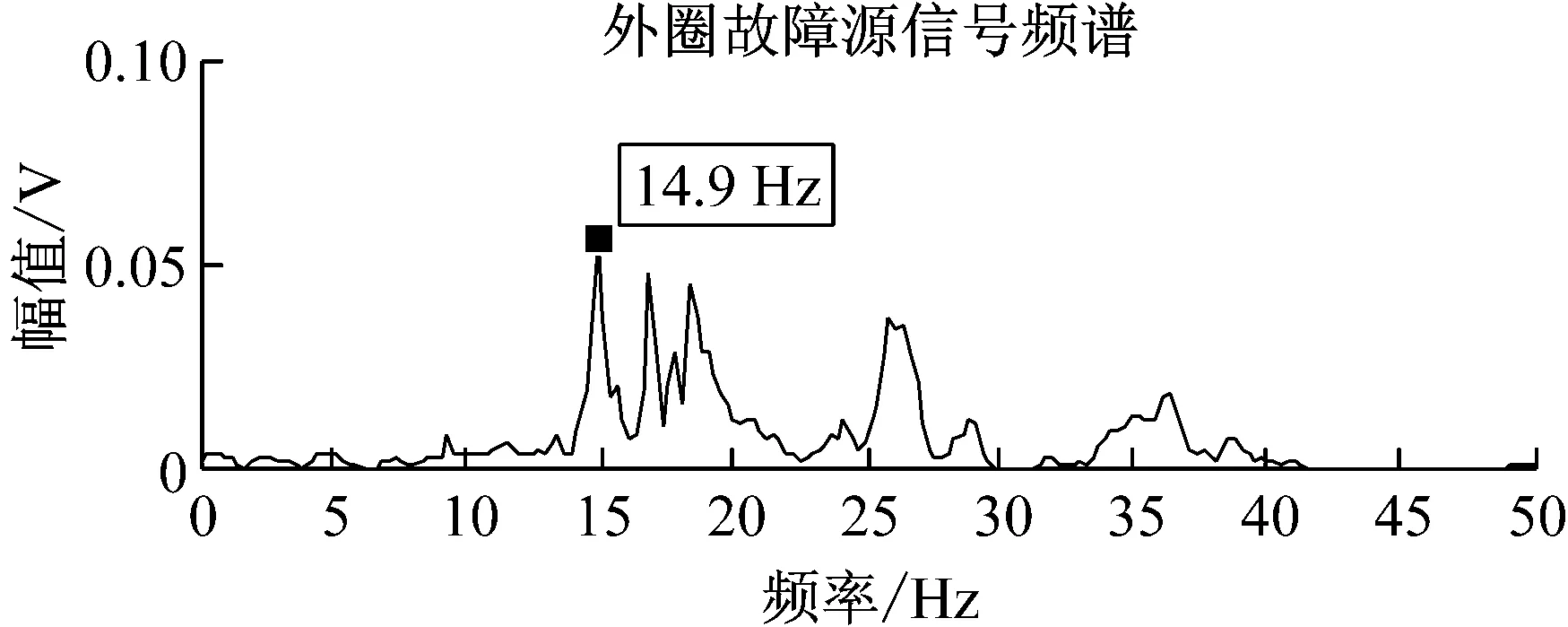
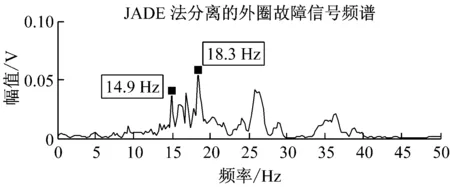
图9 外圈故障源信号与JADE法分离信号的频谱对比

Fig.9 Spectrum comparison between the out-race fault source signals and the separated signals by JADE-ICA

(2) 实测多故障声发射信号仿真

在图4所示的实验台右端安装同时具有外圈和滚柱故障的轴承，声发射传感器的位置如图12所示，利用两个声发射传感器采集信号如图13所示。利用Fast-ICA法和JADE-ICA法进行盲源分离结果如图14和图15所示。

从图14和图15可以看出FAST-ICA分离的两路信号区别不大，分离效果不理想。JADE法分离的两路信号有明显区别，因此对JADE法的分离结果做频谱分析如图16所示。

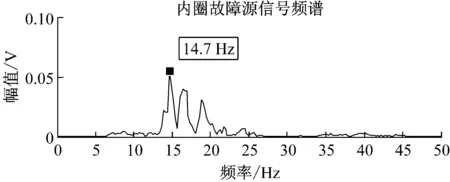
图10 内圈故障源信号与JADE法分离信号的频谱对比

Fig.10 Spectrum comparison between the inner-race fault source signals and the separated signals by JADE-ICA

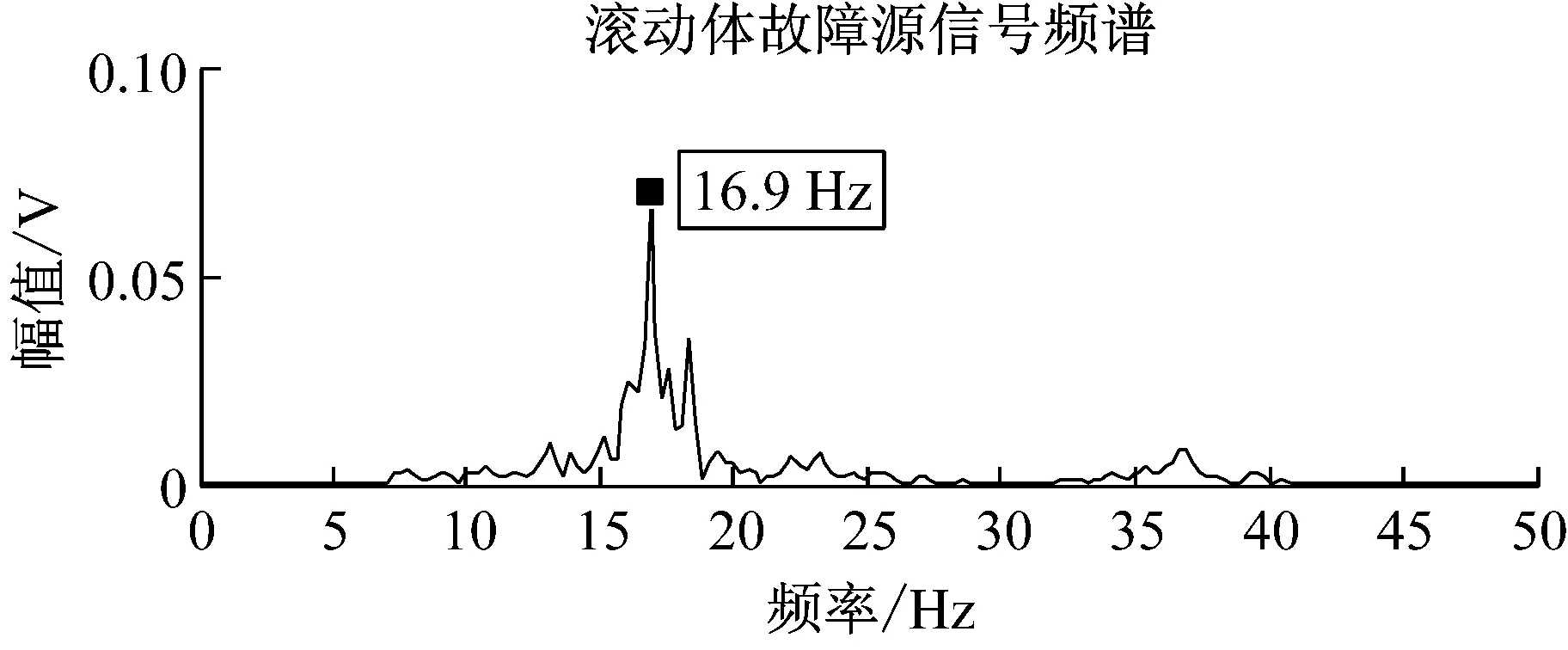
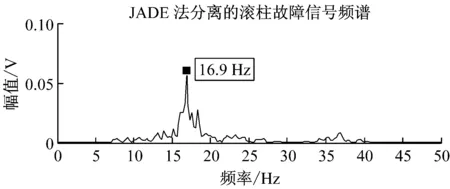
图11 滚柱故障源信号与JADE法分离信号的频谱对比

Fig.11 Spectrum comparison between the rolling element fault source signals and the separated signals by JADE-ICA

图12 声发射传感器安装位置Fig.12 The installation location of AE sensor

与图9、图11比较可以看出，图16中的上图包含外圈故障14.9 Hz的特征频率，下图的频谱峰值包含滚柱故障16.9 Hz的特征频率。图16的频谱分布特征与图9、图11基本符合。

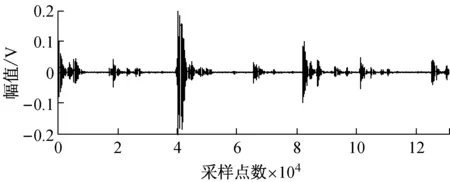
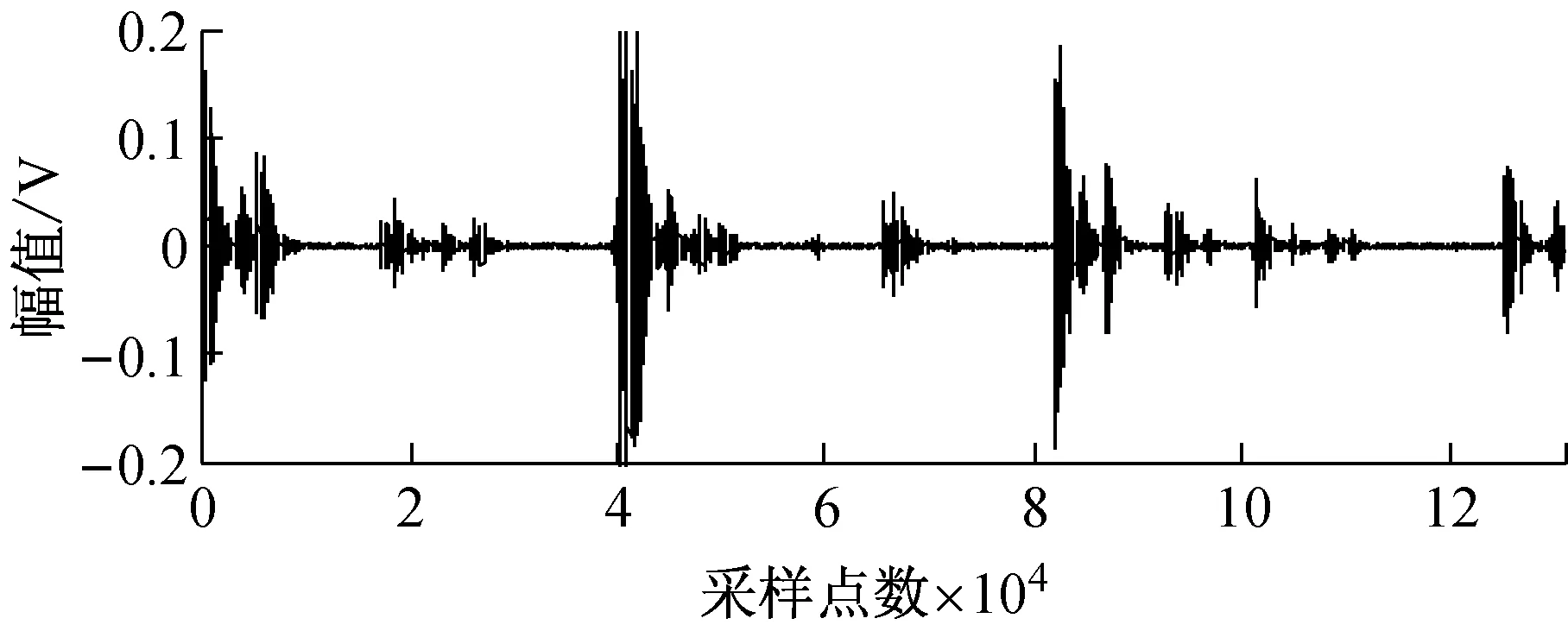
图13 实测多故障波形Fig.13 The waveforms of the measured multi-fault signals

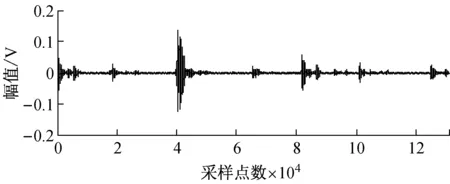
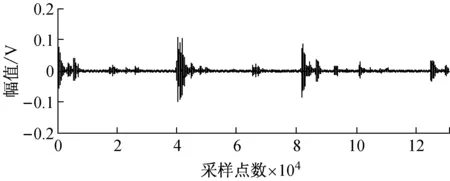
图14 FAST-ICA法分离实测信号波形

Fig.14 The waveforms of the separated measured fault signals by FAST-ICA

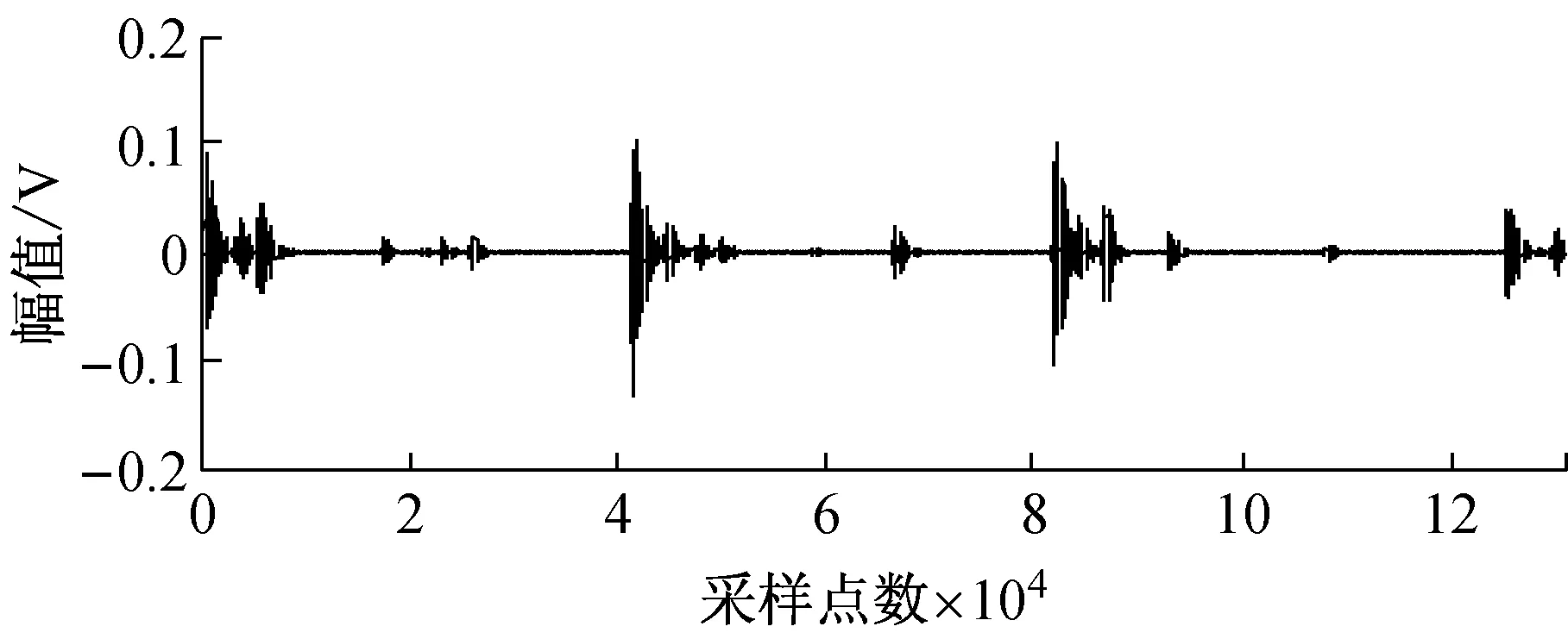
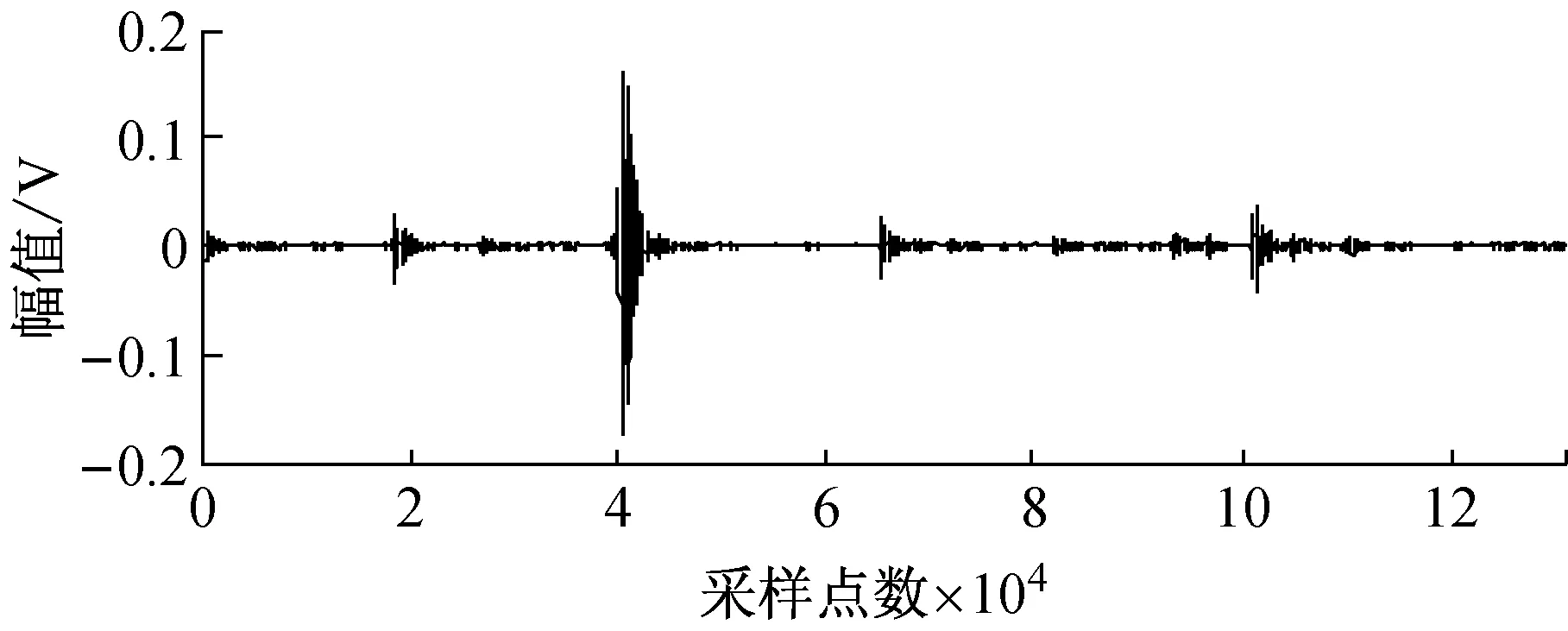
图15 JADE法分离实测信号波形

Fig.15 The waveforms of the separated measured fault signals by JADE-ICA

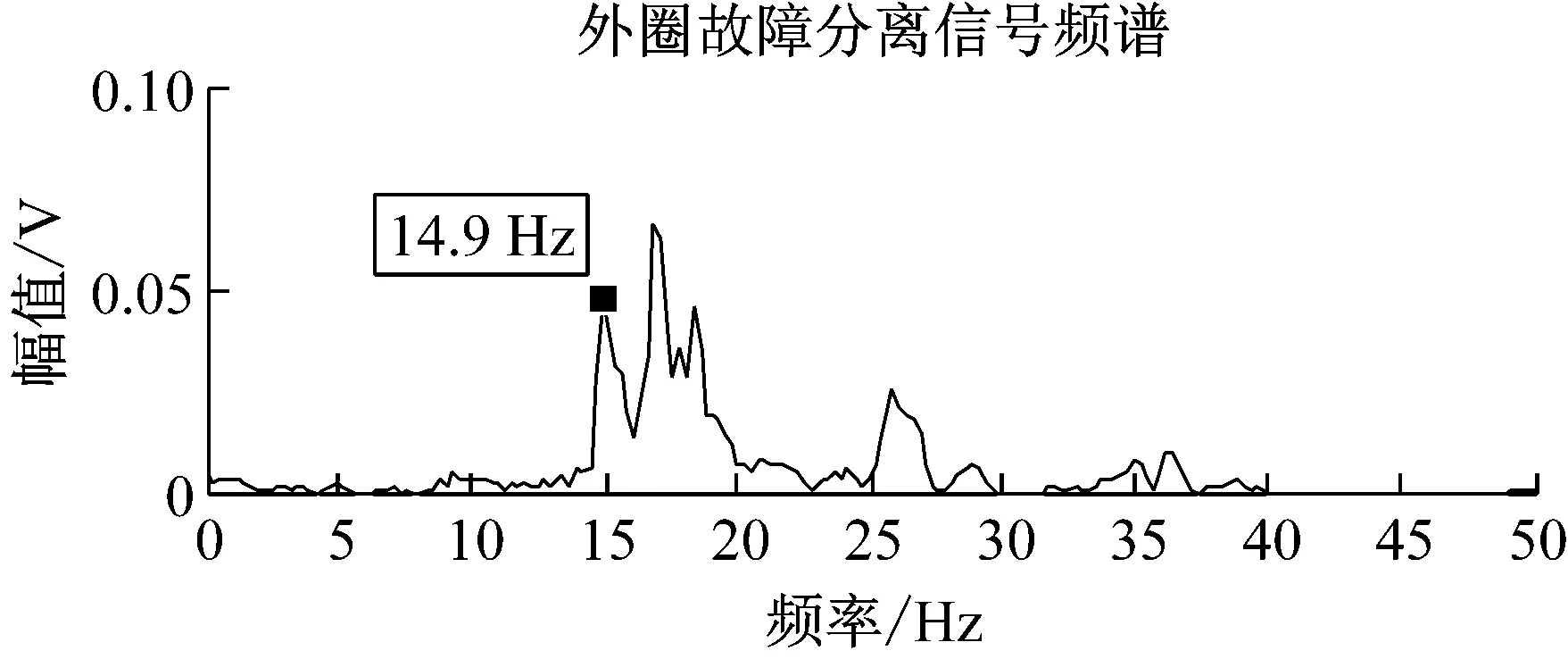
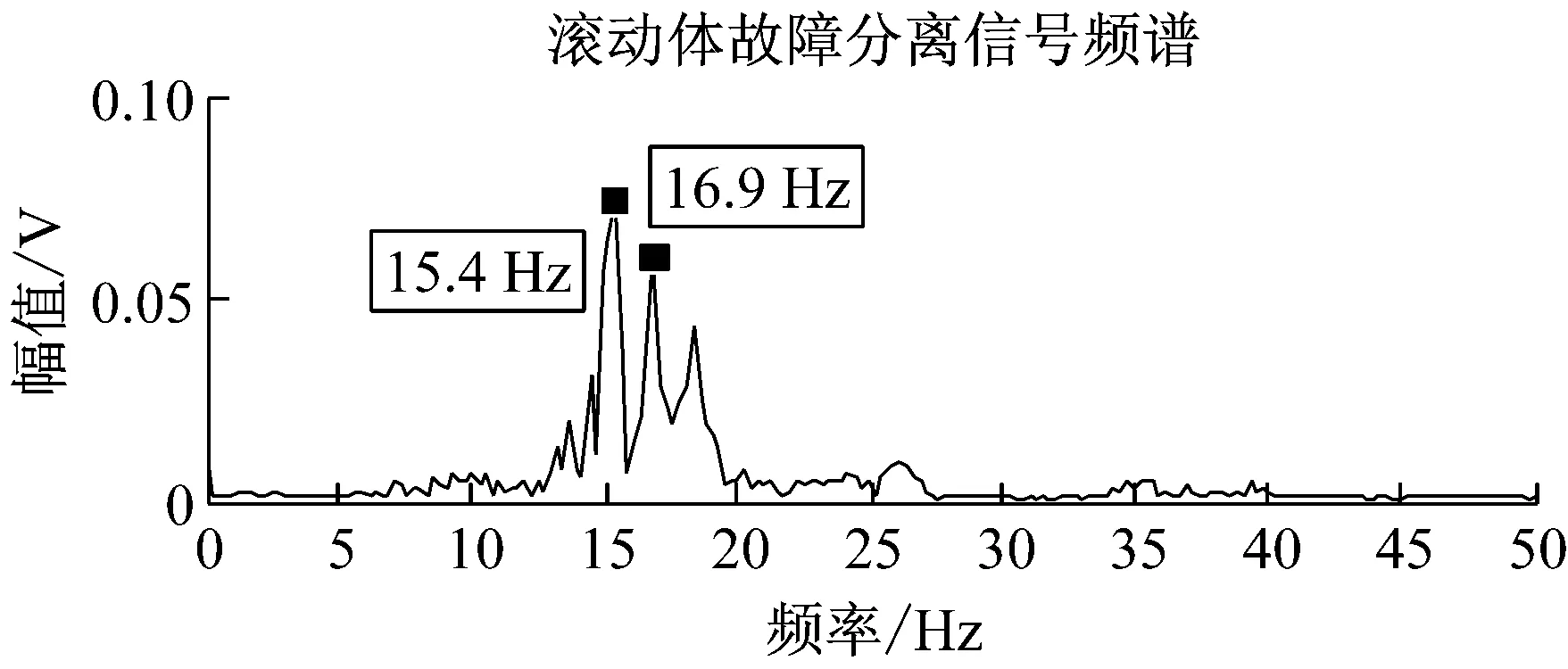
图16 JADE法分离实测频谱

Fig.16 The spectrums of the separated measured fault signals by JADE-ICA

5 结 论

本文研究基于JADE算法的ICA，并将其应用于滚动轴承多故障声发射信号的分离和判断。JADE的联合近似对角化过程可以将源信号和分离信号有效对应，克服时差影响；高阶累积量的高斯噪声不敏感性可以有效克服一类观测噪声的影响。同时选用时域、频域等多个指标组成评价体系对分离结果进行较为全面的评价。仿真结果验证了本文方法的可行性，对进一步开展滚动轴承的状态监测、故障诊断及旋转机械系统的健康维护工作也提供了参考。

[1] 郝如江，卢文秀，褚福磊.声发射检测技术用于滚动轴承故障诊断的研究综述[J].振动与冲击，2008，27(3):75-79.

HAO Rujiang,LU Wenxiu,CHU Fulei, Review of diagnosis of rolling element bearings defaults by means of acoustic emission technique[J].Journal of Vibration and Shock, 2008,27(3) :75-79.

[2] TANDON N, CHOUDHURY A.A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J].Tribology International, 1999, 32: 469-480.

[3] 何沿江，齐明侠，罗红梅.基于ICA和SVM的滚动轴承声发射故障诊断技术[J].振动与冲击，2008，27(3)：150-153.

HE Yanjiang,QI Mingxia,LUO Hongmei, AE based fault diagnosis of rolling bearings by use of ICA and SVM[J].Journal of Vibration and Shock, 2008,27(3): 150-153.

[4] 杨黎明.声发射技术用于段修货车轴承故障诊断研究[D].成都：西南交通大学，2003，11.

[5] 范虹，孟庆丰，张优云，等.基于滤波器组和高阶累积量的信号特征检测.振动与冲击，2007，26(2)：29-32.

FAN Hong,MENG Qingfeng,ZHANG Youyun, et al.Signal feature detection based on filter bank and higher order cumulants[J].Journal of Vibration and Shock, 2007, 26(2): 29-32.

[6] CARDOSO J F, SOULOUMIAC A.Blind beamforming for non Gaussian signals[J].IEE Proc.F: Radar and Signal Process, 1993, 140(6): 362-370.

[7] 王权锋，胥德平，詹泽东，等.金属矿地震数据降噪研究——基于小波域盲分离JADE算法[J].国土资源科技管理，2012，29(6)：106-110.

WANG Quanfeng, XU Deping, ZHAN Zedong, et al.Research on seismic data noise reduction in metallic ore based on wavelet domain blind source separation JADE algorithm[J].Scientific and Technological Management of Land and Resources, 2012, 29(6): 106-110.

[8] 陈恩利，张玺，申永军，等.基于SVD 降噪和盲信号分离的滚动轴承故障诊断[J].振动与冲击，2012，31(23)：185-190.

CHEN Enli, ZHANG Xi, SHEN Yongjun, et al.Fault diagnosis of rolling bearings based on SVD denoising and blind signals separation[J].Journal of Vibration and Shock, 2012,31(23): 185-190.

[9] CARDOSO J F.High-order contrasts for independent component analysis[J].Neural Computation, 1999, 11(1): 157-192.

[10] 张安清.盲分离技术及其在水声信号中的应用研究[D].大连：大连理工大学，2006.

[11] GELLE G,COLAS M,DELAUNAY G.Blind sources separation applied to rotating machines monitoring by acoustical and vibrations analysis[J].Mechanical Systems and Signal Processing, 2000, 14(3):427-442.

[12] CARDOSO J F, LAHELD B.Equivariant adaptive source separation[J].The IEEE Transactions on Signal Processing, 1996, 44(12):3017-3029.

[13] 艾延廷，费成巍，张凤玲，等.ICA在航空发动机振动信号盲源分离中的应用[J].振动、测试与诊断，2010，30(6)：671-674.

AI Yanting,FEI Chengwei,ZHANG Fengling,et al.Blind source separation for aero-engines vibration signalby independent component analysis[J].Journal of Vibration, Measurement& Diagnosis, 2010, 30(6): 671-674.

JADE-ICA-based blind source separation of multi-fault signals of rolling bearings

XI Jianhui, CUI Jianchi, JIANG Liying

(School of Automation, Shenyang Aerospace University, Shenyang 110136, China)

Here, a joint approximate diagonalization of eigen-matrix and independent component analysis (JADE-ICA) method based on the high-order statistics of source signals was studied.It was applied to the blind source separation of rolling bearing faults’ acoustic emission (AE) signals.The multi-AE source signals of rolling bearings were collected with multi-sensor.It was shown that the bolling bearing multi-AE source signals have characteristics, such as, time difference among multi-signals, with decay and quasi periodicity.Through the maximum joint approximate diagonalization, the one-to-one match between source signals and separated signals was realized to overcome the influence of nonlinearity and time difference.With the insensitivity of high-order statistics to Gaussian noise, the effects of random measured noise on the separated results were effectively suppressed.Correlation coefficient, quadratic residual, performance index and spectral characteristics were chosen to form a set of time-frequency domain evaluation indexes to verify the separated results.The simulation results verified the feasibility and effectiveness of the proposed method.

JADE; rolling bearing; fault diagnosis; acoustic emission

国家自然科学基金青年基金(60804025)；辽宁省教育厅科学技术研究项目(L2014069；L2013070)；沈阳市科技创新团队项目(SRC201204)

2015-07-14 修改稿收到日期：2016-02-24

席剑辉 女，博士，副教授，硕士导师，1975年6月生

TP306

A

10.13465/j.cnki.jvs.2017.05.037