匀质地下管线沉降的傅里叶级数解

杨成永，程　霖, 余　乐，韩薛果

(1.北京交通大学 土木建筑工程学院，北京　100044； 2.北京城市快轨建设管理有限公司，北京　100027)

隧道开挖将引起土层及土层中邻近地下管线的沉降。管线沉降变形的理论分析一般采用弹性地基梁方法，并且根据变形的大小，可以分为小变形和大变形力学方法。

小变形力学方法的研究成果较多，主要有：Attewell等(1986)[1]假定地层沉降符合Peck曲线，采用弹性地基梁法分析管线与隧道平行和垂直时管线的响应；Vorster(2005) 等[2]采用弹性地基梁法推导了隧道开挖对邻近匀质管线的最大附加弯矩计算公式；Klar(2005) 等[3]比较了Winkler地基与弹性连续体地基的不同，根据更精细的弹性连续体地基的解答，提出了修正的Winkler地基模量；王霆等(2006)[4]从地下管线的失效模式、管土相互作用、简化算法、离心模型试验及数值模拟等方面，综述了隧道施工对地下管线影响的研究成果；骆建军等(2006)[5]就北京地铁黄庄站施工对地下管线的影响进行了数值计算、现场监测和安全性评价；Klar等(2007)[6]采用边界积分方法研究了土层中管线的沉降变形，探讨了管线周围局部土层屈服的影响；吴为义等(2008)[7]采用弹性地基梁理论及FLAC3D软件计算了盾构下穿时电力管沟的沉降变形及内力；孙宇坤等(2009)[8]对盾构隧道下穿煤气管线进行了沉降监测，分析了管线的沉降变形规律；张坤勇等(2010)[9]对弹性地基无限长梁的控制微分方程进行了解析求解，假定土层的位移函数及管线位移的特解均可用多项式表达，然后根据边界条件及不同区段间的连续性条件确定积分系数；姜玲等(2010)[10]对弹性地基无限长梁的控制微分方程进行了初参数法解析求解，土层的位移函数采用Peck公式。

大变形力学方法方面，杨成永等(2014)[11]建立了考虑管线轴力的控制微分方程，假定管线的轴向伸长在沉降槽范围内为一常量，给出了管线与隧道垂直情况下管线大变形的近似解。

上述既有研究成果表明，将管线视为承受土层位移荷载的弹性地基梁，对其在小变形力学方法方面的研究已较充分；但大变形力学方法方面的研究还有待深入：一方面既有近似解的计算精度有待探究；另一方面，近似解只能适用于管线只承受土层荷载且土层及管线的沉降曲线均为Peck曲线的情况，适用范围相当有限。因此需要探讨管土共同作用下管线大变形问题求解的新方法。

无限长匀质地下管线(以下简称为管线)属于一维杆件。对于一维杆件沉降的微分方程，均可用傅里叶级数进行求解[12-13]，并且傅里叶级数解的精度高，可以视为微分方程的精确解，而且可以用于判断打靶法或其他近似方法计算结果的精度。

本文针对地铁盾构隧道开挖引起邻近管线沉降较大的情况，列出管线大变形的控制微分方程，推导土层沉降及管线沉降的傅里叶级数系数计算公式，给出沉降和内力的计算公式；基于文献[11]中的数据，采用推导的变形和内力计算公式计算管线沉降随土层沉降的级数解，并与近似解的求解结果进行对比，验证级数解的正确性。

1　管线大变形的控制微分方程

管线微元的受力如图1所示。图中：w为管线沉降，m，向上为正；x和y为管线坐标，m；坐标原点位于沉降槽中心；N为管线轴力，N；注意这里直接将N表示其物理分量，而文献[11]中该处为g1N；g1为管线的一维度规(管线变形后长度与变形前长度的比)；Q为管线剪力，N；M为管线弯矩，N·m。根据图1可得管线大变形的控制微分方程为[11]

(1)

式中：E为管线弹性模量，Pa；I为管线截面的惯性矩，m4；q为管线右端单位荷载，N·m，向上为正。

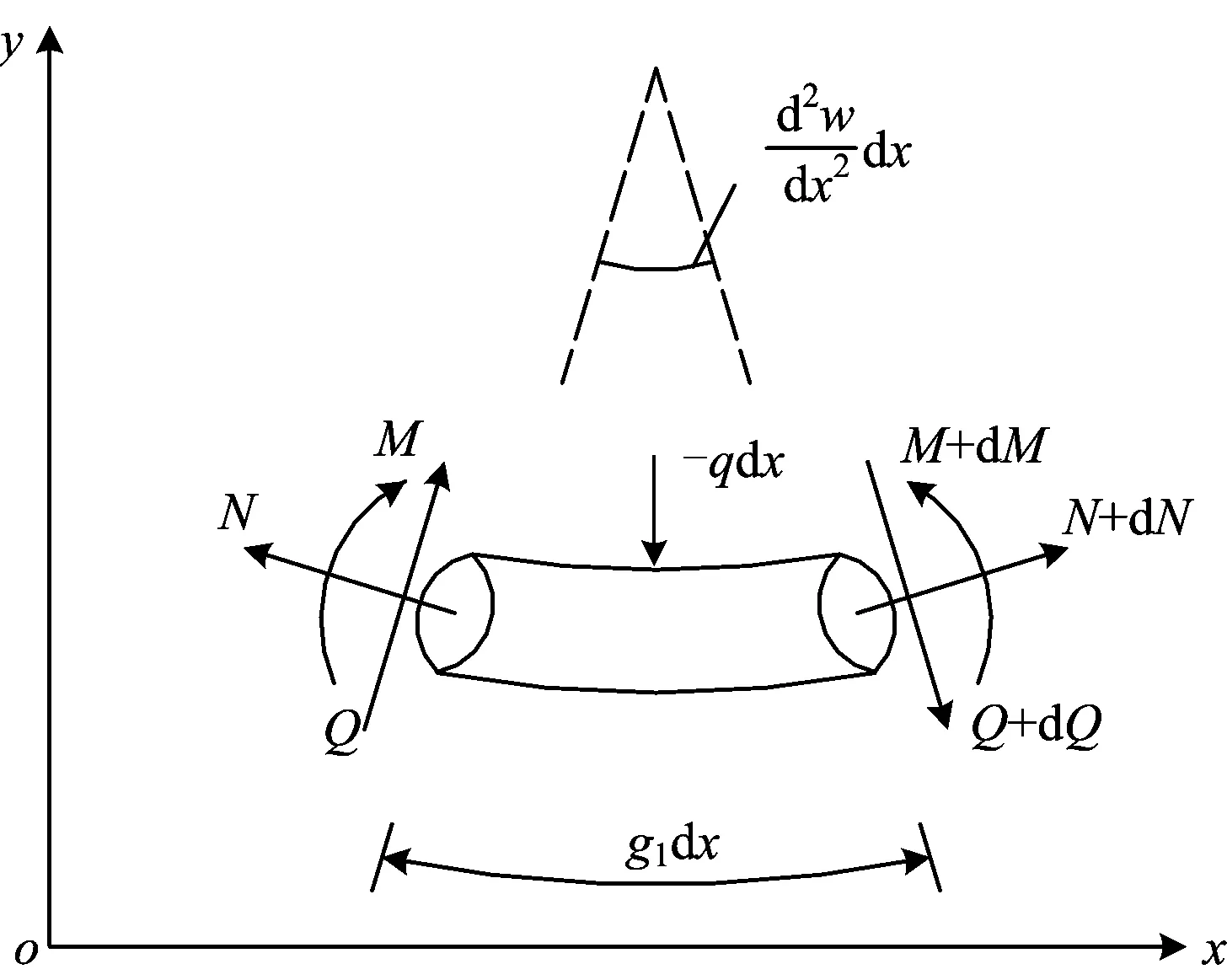
图1　管线微元受力示意图

考虑管线为无限长管线，微分方程(1)的边界条件可视为两端固支，并且由于对称，中点的转角也为0，有

(2)

式(1)和式(2)组成所求解的边值问题，而边值问题中的参数可分别按照如下公式计算得到。

(1)管线右端荷载q按Winkler地基反力计算。

考虑管线沉降是由土层沉降所引起的，地基反力的计算公式为

q=kD(S-w)

(3)

式中：k为地基系数，Pa·m-1；D为管线外径，m；S为土层沉降，m。

土层及管线的沉降变形如图2所示。图中：S0和w0为x=0处土层及管线的最大沉降，m；i和j分别为土层及管线的沉降槽宽度，即沉降曲线反弯点距x=0处的水平距离，m。

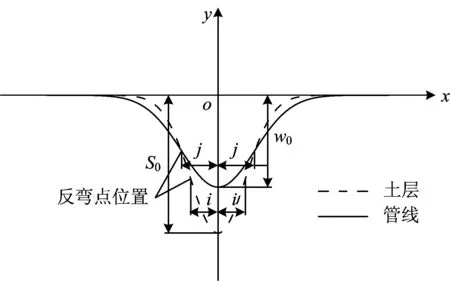
图2　土层及管线的沉降示意图

参照图2，式(3)中土层沉降S可用Peck曲线表示为

(4)

(2)在式(1)中除管线沉降w外，g1和N也是待求的量。

为了降低式(1)的非线性程度，假设沉降槽附近范围内管线的轴向变形和轴力是均匀的，并且管线沉降后的长度按Peck曲线进行计算，即假定用于管线长度计算的沉降曲线为

(5)

因此有[11]

(6)

(7)

式中：A为管线的截面积，m2；L为计算范围的半宽，m。

(3)由梁的弯矩与曲率间的关系可计算管线弯矩M，再根据管线剪力Q与管线弯矩M间的关系可计算管线剪力，分别如下

(8)

(9)

2　基于傅里叶级数的计算公式

为了对式(1)采用傅里叶级数求解，需要把式(1)和式(3)中的S及w均展开成三角级数。由于土层沉降及管线截面和约束关于沉降槽中心对称，管线沉降势必也是对称的，因此可把土层沉降S在[-L, +L]上展成余弦级数，即

(10)

其中，

(11)

(12)

式中：S(x)为土层沉降，m；b0和bn为傅里叶级数的系数；n为自然数。

为使计算范围足够大，L一般取3i以上。利用式(4)、式(11)和式(12)有[14]

(13)

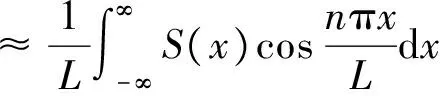
(14)

把管线沉降w在[-L, +L]上同样展成余弦级数，即

(15)

式中：w(x)为管线沉降，m；a0和an为待求的傅里叶级数的系数。

根据式(15)，管线沉降的各阶导数为

(16)

(17)

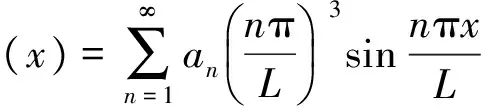
(18)

(19)

把式(13)和式(14)代入式(10)，然后把式(10)和式(15)代入式(3)，最后再将式(3)、式(17)和式(19)带入式(1)，比较常数项及三角函数的系数，得到式(15)的系数为

a0=b0

(20)

(21)

需要说明的是：式(15)在计算区间的端点和中点时已经满足式(2)所示的边界条件；而且式(15)有各阶导数，可以通过增大n的值达到任意精度。式(15)与式(5)的区别是：式(15)是本文的求解目标，它不一定是Peck曲线；式(5)仅是在近似计算轴力及度规时需要用到；式(15)中的系数a0和an是通过级数的方法确定的，而式(5)中的参数w0和j目前只能采用近似方法确定；在已知a0和an后，可以计算w0和j，但反过来则不行。

比较式(5)和式(15)，有

(22)

至于式(5)中的j，可以通过式(17)计算管线沉降曲线的曲率，其正负变号之处对应的x的值即为j。用公式表示时，j为如下方程的根：

(23)

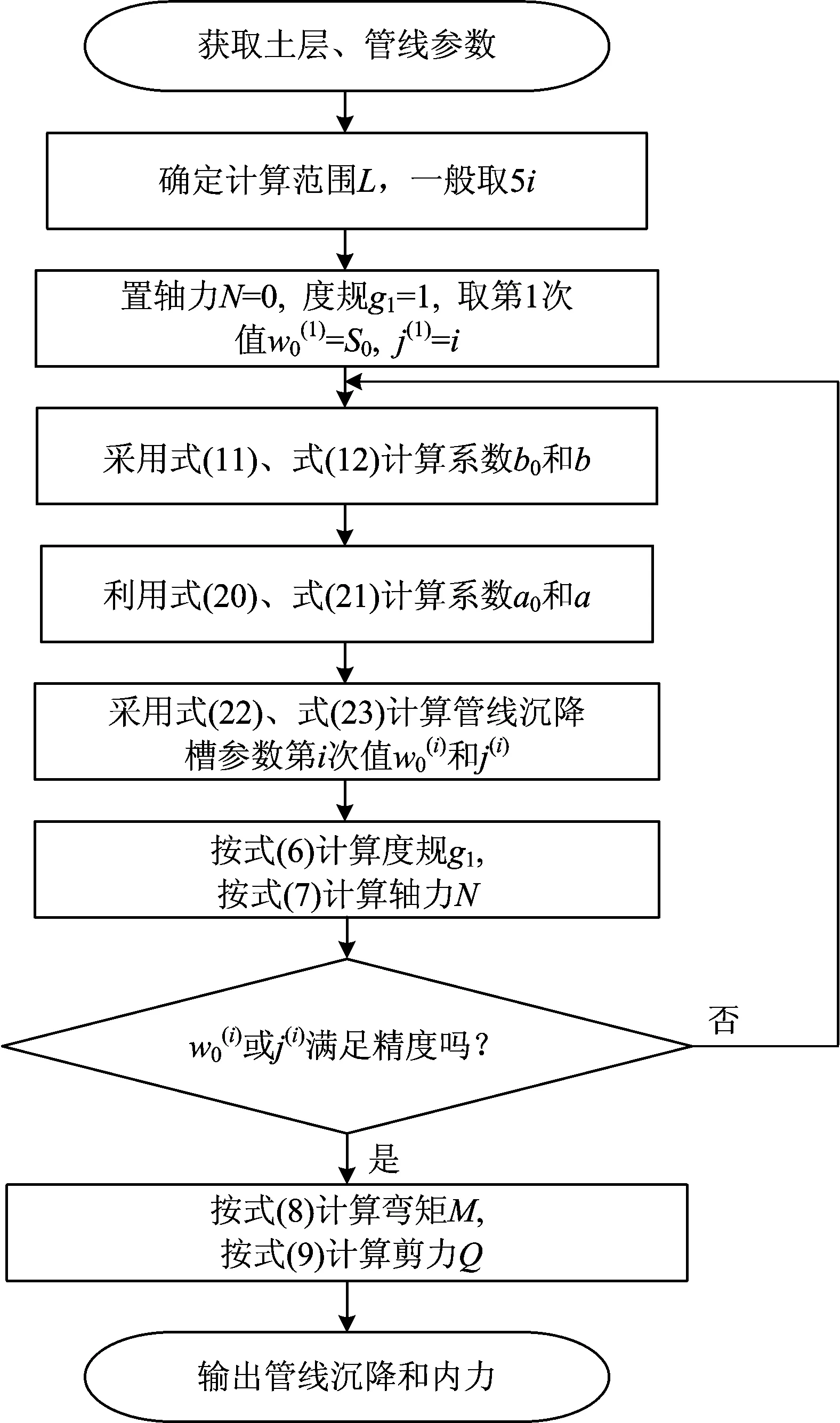
图3　管线沉降和内力的计算框图

至此，若土层沉降参数S0及i，地基系数k，以及管线参数A，E，I，D均已知，则可计算得到管线的沉降和内力，计算框图如图3所示。

3　实例计算

采用文献[11]的工点数据：土层最大沉降S0分别取0.05，0.90，1.80 m；土层沉降槽宽度i=1.8 m，地基系数k=8×107Pa·m-1，管线外径D=426 mm，管线截面惯性矩I=1.746×108mm4，管线弹性模量E=2×1011Pa。

采用C语言编程实现本文的计算方法，对于该实例计算得到的级数解列于表1。为对比分析，将文献[11]计算的近似解也列于表1中。不同土层最大沉降时土层和管线沉降的级数解曲线如图4所示 。

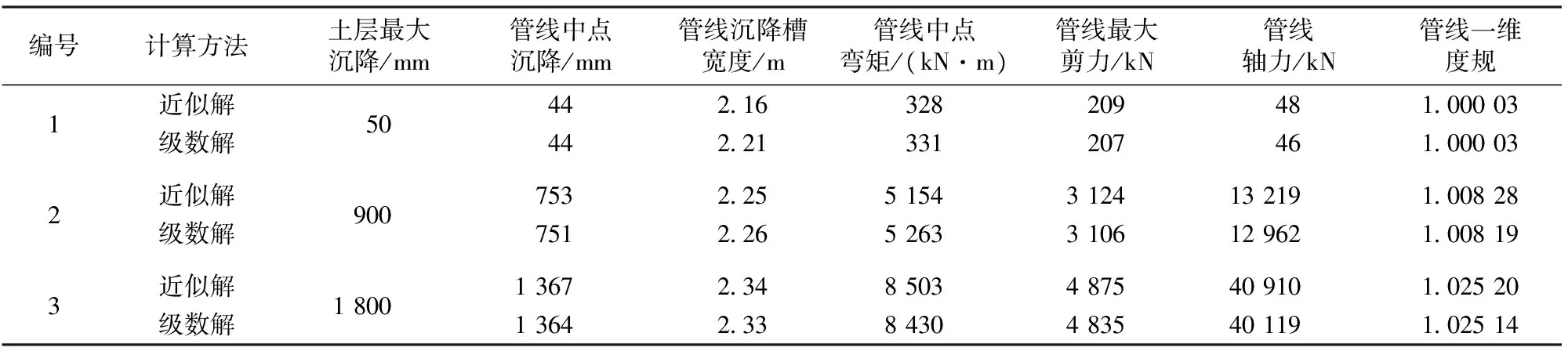
表1　计算结果

图4　不同土层最大沉降时土层和管线的沉降曲线

从表1及图4可以得出如下结论。

(1)管线沉降曲线与正态曲线十分接近。也就是说，在土层沉降曲线为Peck曲线的情况下，管线沉降曲线的形式也是Peck曲线。

(2)文献[11]所得的近似解与本文级数解的计算结果比较接近。近似解的计算精度能够接近级数解的原因在于：“管线沉降符合Peck曲线”的假定与实际吻合；近似解选择了2个合适的位置(x=0及x=j)计算管线沉降槽的参数。

从求解过程来看，级数解比文献[11]的近似解有如下优越性。

(1)级数解不需要事先假定管线沉降曲线的形式。

(2)级数解除土层位移荷载外，还可以处理其他的荷载形式。对近似解来说，在管线上增加土层位移荷载以外的其他荷载，将使管线变形后不再为Peck曲线，难于求解。

(3)级数解随所取级数项数的增加，求解精度稳定提高。近似解求解结果的精度与选取的计算点位置有关，位置不同，结果的精度亦不同。

4　结　语

本文采用傅里叶级数求解管线的非线性沉降问题，得到了满意的结果。级数解本身可以通过增加级数项数达到任意精度。但本文“在沉降槽附近范围内管线均匀伸缩”的假定仍会带来计算结果的近似性，当然这一假设与级数方法本身无关。在土层对管线握裹力不大的情况下，或者管线外表面比较光滑时，这种假设所所产生的影响更小。

级数解可以处理较为复杂的荷载形式，如管线上作用有集中荷载，或者土层抗力只作用在管线的部分区段上等。当然，在处理这些复杂荷载时，傅里叶级数的系数一般不能直接得到显式表达，需要求解线性方程组。

关于小变形情况下地埋管线沉降的傅里叶级数解，因为其只是大变形公式在轴力和伸长均等于零时的特殊情况，所以本文未进行讨论。

[1]ATTEWELL P B, YEATES J, SELBY A R. Soil Movements Induced by Tunnelling and Their Effects on Pipelines and Structures [M]. London: Blackie and Son Ltd, 1986.

[2]VORSTER T E B, KLAR Assaf, SOGA Kenichi, et al. Estimating the Effects of Tunneling on Existing Pipelines [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(11): 1399-1410.

[3]KLAR A, VORSTER T E B, SOGA K, et al. Soil-Pipe Interaction Due to Tunnelling: Comparison between Winkler and Elastic Continuum Solutions [J]. Geotechnique, 2005, 55(6): 461-466.

[4]王霆，刘维宁，李兴高，等.地铁施工影响邻近管线的研究现状与展望[J].中国铁道科学，2006，27(6)：117-123.

(WANG Ting, LIU Weining, LI Xinggao, et al. Current Situation and Prospect of Studies on Tunneling-Induced Effect of Adjacent Pipelines [J]. China Railway Science, 2006, 27(6): 117-123. in Chinese)

[5]骆建军，张顶立，王梦恕，等.地铁施工对管线的影响[J].中国铁道科学，2006，27(6)：124-128.

(LUO Jianjun, ZHANG Dingli, WANG Mengshu,et al. Influence of Metro Construction on Underground Pipeline [J]. China Railway Science, 2006, 27(6)：124-128. in Chinese)

[6]KLAR A， VORSTER T E B， SOGA K，et al. Elastoplastic Solution for Soil-Pipe-Tunnel Interaction [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(7): 782-792.

[7]吴为义，孙宇坤，张土乔.盾构隧道施工对邻近地下管线影响分析[J].中国铁道科学，2008，29(3)：58-62.

(WU Weiyi，SUN Yukun，ZHANG Tuqiao. Analysis of the Effects on the Adjacent Underground Pipelines by Shield Tunneling Construction [J]. China Railway Science, 2008，29(3)：58-62. in Chinese)

[8]孙宇坤，吴为义，张土乔.软土地区盾构隧道穿越地下管线引起的管线沉降分析[J].中国铁道科学，2009，30(1)：80-85.

(SUN Yukun，WU Weiyi， ZHANG Tuqiao. Analysis on the Pipeline Settlement in Soft Ground Induced by Shield Tunneling across Buried Pipeline [J]. China Railway Science, 2009，30(1)：80-85. in Chinese)

[9]张坤勇，王宇，艾英钵.任意荷载下管土相互作用解答[J]. 岩土工程学报，2010，32(8)：1189-1193.

(ZHANG Kunyong, WANG Yu, AI Yingbo. Analytical Solution to Interaction between Pipelines and Soils under Arbitrary Loads [J]. Chinese Journal of Geotechnical Engineering, 2010, 32(8): 1189-1193. in Chinese)

[10]姜玲，汪中卫，王旭东.隧道开挖引起地下管线竖向位移的初参数法求解[J]. 南京工业大学学报:自然科学版，2010，32(4)：72-76.

(JIANG Ling, WANG Zhongwei, WANG Xudong. Initial Parameter Method for Solving Vertical Displacement of Buried Pipelines Caused by Tunnel Excavation [J]. Journal of Nanjing University of Technology: Natural Science Edition, 2010, 32(4): 72-76. in Chinese)

[11]杨成永，张彦斌，张伦政. 匀质地下管线大变形的控制微分方程及其近似解 [J]. 中国铁道科学，2014，35(1)：42-46.

(YANG Chengyong, ZHANG Yanbin, ZHANG Lunzheng. Governing Differential Equation and Approximate Solution for Large Deformation of Jointless Underground Pipeline [J]. China Railway Science, 2014，35(1)：42-46. in Chinese)

[12]严宗达.结构力学中的傅里叶级数解法 [M]. 天津:天津大学出版社，1989.

[13]杨维加.弹性地基梁的三角级数解法[M]. 北京：水利水电出版社，2005.

[14]数学手册编写组.数学手册 [M]. 北京：高等教育出版社，1979.