基于影响矩阵理论的悬索桥索力优化

王会利，秦泗凤，李盛洋

(1.大连理工大学 土木工程学院，辽宁 大连　116023； 2.大连大学 材料破坏力学数值试验研究中心，辽宁 大连　116022； 3.湖北省交通规划设计院股份有限公司，湖北 武汉　430051)

悬索桥具有较强的几何非线性，悬索系统在无应力状态下是无法成形的，只有在荷载和索力作用下缆索系统构形才能稳定，满足平衡方程。缆索系统最终稳定的构形是在相应荷载下的理想线形，理想线形对应着理想索力，即这个“找形”的过程也就是索力优化的过程。

很多学者对悬索桥索力优化或“找形”展开研究。Vu[1]应用非线性缆索单元分析缆索承重桥，他将抛物线作为初始线形，加快了计算收敛速度。Kim[2]基于Newton-Raphson迭代方法，应用弹性悬链线单元，优化了悬索桥在恒载下的线形，并在此基础上，通过初始力消除塔梁的初始变形，获得更精确的结果。Myung-Rag Jung[3]通过设置弹性悬链线单元的无应力长度，得到悬索桥非线性缆索单元广义切线刚度矩阵，进而对结果进行求解。Huu-Tai Thai[4]应用弹性悬链线单元，同时考虑了材料非线性对多跨悬索桥进行索力优化。唐茂林[5]提出了节段悬链线法。罗喜恒[6]应用割线刚度，发展完善了节段悬链线法，推导了缆索单元刚度的精确表达式。王超[7]等以最小弯曲应变能法为理论基础，引入优化理论，运用通用有限元软件ANSYS与自主研发的SiPESC.OPT软件系统对悬索桥进行索力优化。

影响矩阵法多用于斜拉桥、拱桥的索力优化[8-9]，在悬索桥施工调索过程中也有所应用[10]。但是悬索桥初期找形过程具有较强的非线性[11]，目前还未见在悬索桥索力优化方面应用的报道。本文基于非线性有限元，在初始刚度的基础上计算悬索桥影响矩阵，通过迭代计算分析，完成悬索桥索力优化。

1　悬索桥影响矩阵

1.1　影响矩阵

假设图1所示的悬索桥有n根索。定义索力向

图1　结构示意图

量为F=(f1,f2,…,fn)T，对应主梁上拉索锚固点的位移向量为D=(d1,d2,…,dn)T。

当某根索的索力fi发生索力变化Δi(i=1,2,…，n)时，D也随之改变，令变化量为Ai=(a1i,a2i,…,ani)T。如果每根索都发生索力变化，且对应的索力变化对角矩阵为Δ=Diga(Δ1,Δ2,…,Δn) ，那么D的变化量矩阵为

A=(A1A2…An)

(1)

式中：A为结构的影响矩阵。

1.2　悬索桥影响矩阵的形成

将悬索桥恒载和初始索力定义为悬索桥的初始荷载。在初始荷载作用下，悬索桥具有的刚度称为悬索桥的初始刚度。本文在考虑悬索桥初始刚度的基础上，形成悬索桥结构的影响矩阵。具体过程如下：

第1步，假定初始索力F0和初始主缆线形，计算初始荷载作用下悬索桥关键点的位移D0，一般情况下，关键点可以取主梁和主缆上的吊点；

第2步，计算在初始荷载和第i根索的索力变化值Δi作用下关键点的位移Di；

第3步，考虑悬索桥的初始刚度后，悬索桥基本属于线性结构[12]，根据叠加原理，通过Ai=Di-D0得到在第i根索索力变化值Δi作用下关键点的位移变化量；

第4步，重复上述过程，得到影响矩阵A=(A1A2…An)。

2　基于影响矩阵的悬索桥索力优化

在确定优化目标后，即确定关键点的位移向量D后，通过求解方程AF=ΔD，就能得到索力向量F=A-1ΔD。由于悬索桥属于非线性结构，需要迭代逼近优化目标D，因此其索力优化是个迭代的过程，具体如下：

第1步，在形成影响矩阵的基础上,索力向量F0更新为F1,F1=F0+A-1Δ(D-D0)；

第2步，将F1带入有限元模型，计算悬索桥在恒载和F1作用下的结构位移向量D1；

第3步，索力向量F1更新为F2,F2=F1+A-1Δ(D-D1)；

第4步，将F2带入有限元模型，计算悬索桥在恒载和F2作用下的结构反应D2；

第5步，重复第2步—第4步，直到‖D-Dj‖<ε，得到最终的理想索力Fj,其中j为循环次数，j=1,2，…。

理想索力对应的缆索系统形状就是悬索桥合理成桥线形。流程如图2所示。

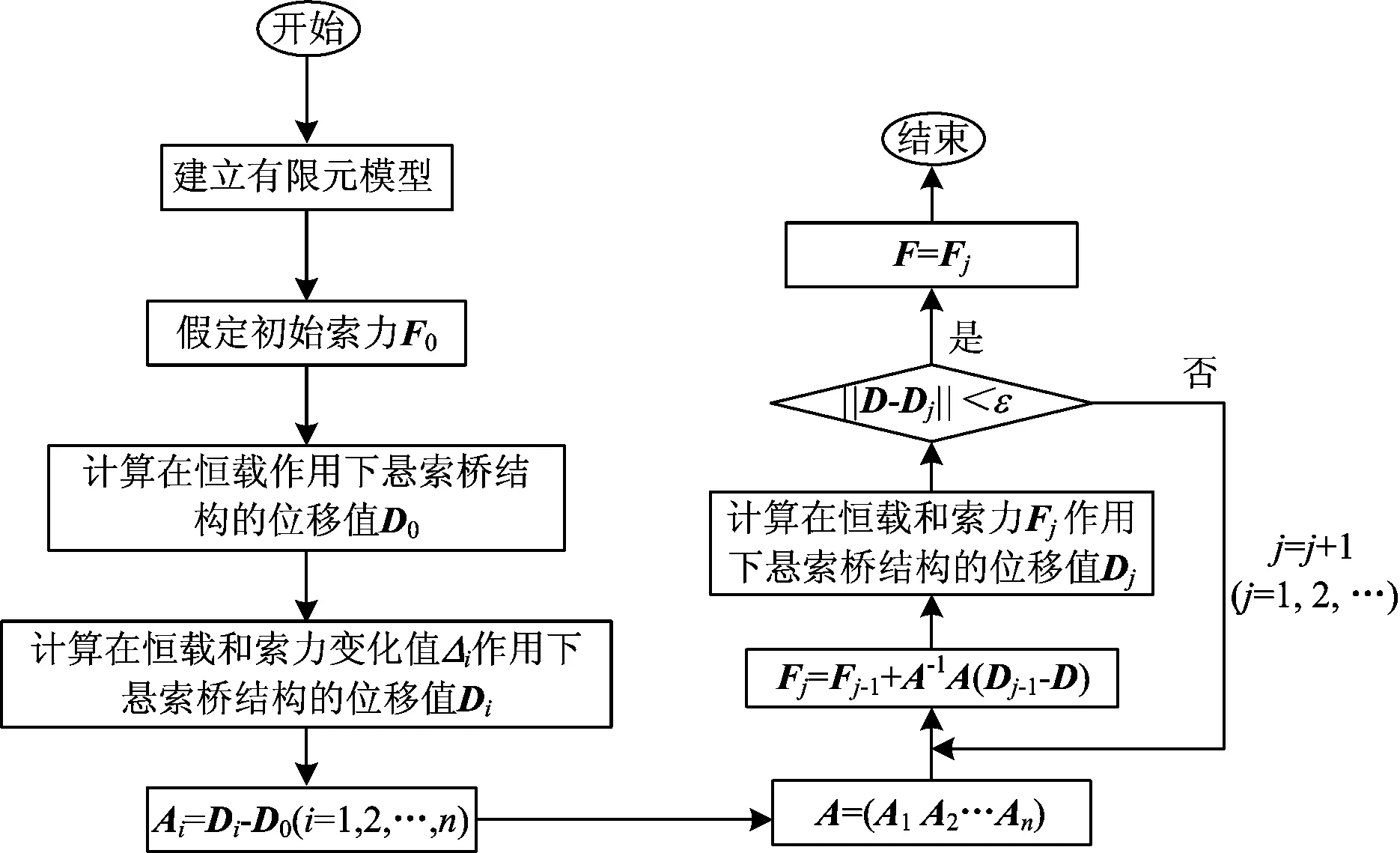
图2　流程图

初始索力F0和初始主缆线形会影响收敛进程，因此需要先估算索力和主缆线形，再进行优化计算。严格来说，主缆成桥线形是多段悬链线[13]，但是为了计算简便，一般可以假设主缆初始线形为抛物线，并按内力平衡法估算吊杆和主缆的初始索力[14]。

3　验　证

以图3所示悬索结构为例，验证上述方法的可行性。

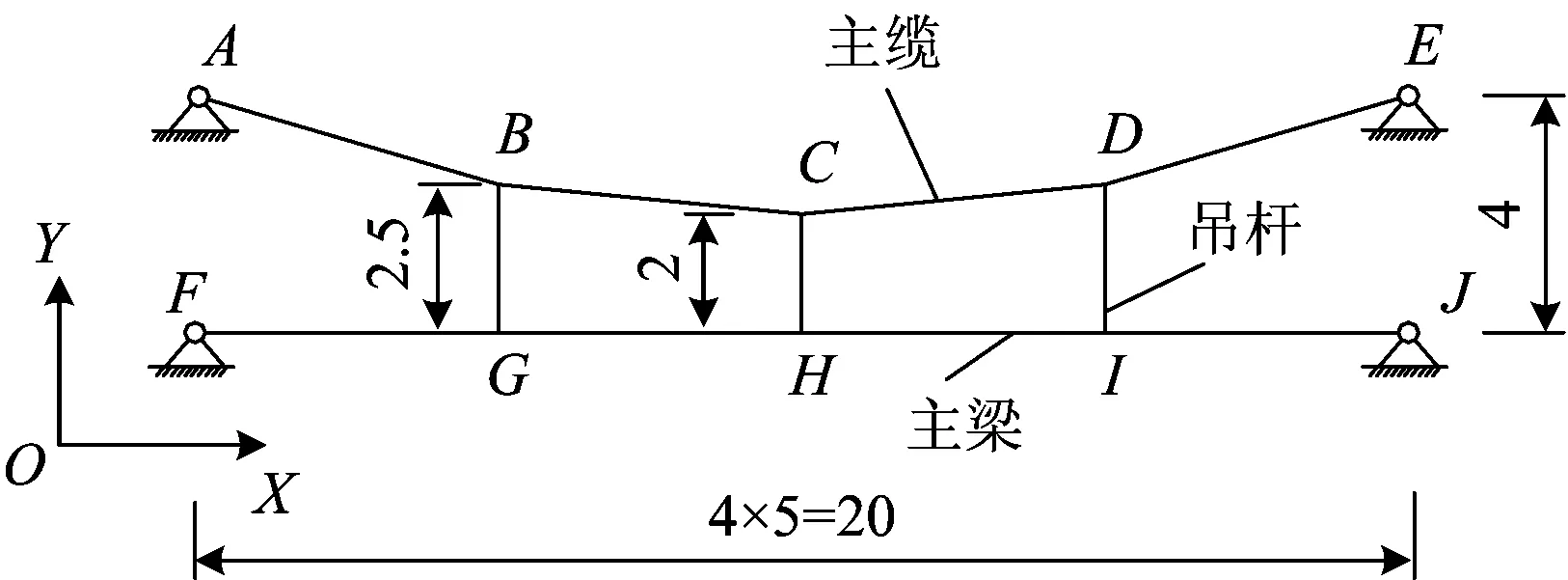
图3　某悬索结构 (单位：m)

在图3所示悬索结构中，有4段主缆，3个吊杆。主梁和主缆跨度均为20 m。主缆的截面面积为1.398×10-2m2，吊杆的截面面积为8.84×10-3m2，二者抗弯惯性矩为0 m4，不承担弯矩。主缆和吊杆采用高强平行钢丝，材料弹性模量为190 GPa。主梁的截面面积为0.84 m2，抗弯惯性矩为5.488×10-3m4，采用Q345钢材，材料弹性模量为210 GPa。在主梁上作用均布荷载20 kN·m-1。

3.1　优化目标

优化目标包括：

(1) 吊杆保持竖直，B，C和D点没有水平位移，即dxB=dxC=dxD=0；

(2) 主梁弯矩最小，G，H和I点没有竖向位移，即dyG=dyH=dyI=0；

(3) 矢高不变，C点没有竖向位移，即dyC=0。

未知索力包括4段主缆的索力fAB，fBC，fCD和fDE，以及3段吊杆的索力fBG，fCH和fDI，即

F=(fAB,fBC,fCD,fDE,fBG,fCH,fDI)T

(2)

3.2　优化过程

按内力平衡法初步估算吊杆和主缆的初始索力，得到主缆和吊杆的初始索力为100 kN，即F0=(100,100,100,100,100,100,100)T；令主缆单元索力变化值为10 000 kN，吊杆单元索力变化值1 000 kN，即Δ=Diga(10 00010 00010 00010 0001 0001 0001 000)。根据上述方法，经过有限元计算，得到结构的影响矩阵为

(3)

经过4轮迭代后‖D-D4‖<0.01，所以索力

F4=(-6 386.26,3 579.63,3 568.88,

-6 385.14,34 855.19,141.06,

3 4849.18)T

因为F是体内力[9]，所以在结果中会有负值。位移和索力的收敛过程如图4和图5所示。从图中可以看出，经过2轮迭代，计算就基本收敛。

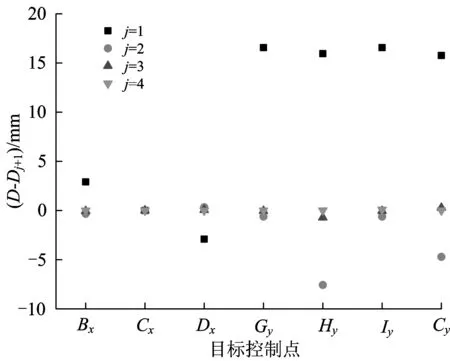
图4　位移收敛过程

3.3　优化结果

将F4带入有限元模型中，可以得到悬索结构的最终状态，结构的位移和索力如图6和图7所示。因为B，C和D点的水平位移为0，所以没有示出。从图中可以看出，结果满足提出的优化目标，同时索力均匀。B和D点竖向位移较大，这是由于在相应的荷载作用下，主缆的初始线形不合理，而变形后主缆的线形才合理。

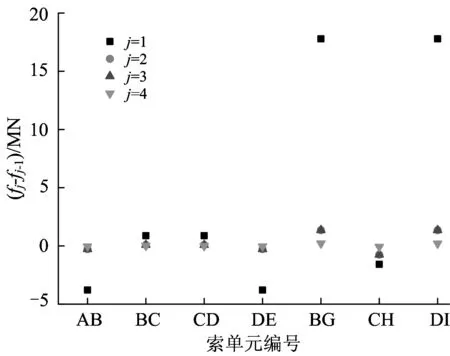
图5　索力收敛过程

图6　主梁、主缆位移

图7　主缆、吊杆索力(单位：kN)

从上面的计算结果可以看出，本方法是可行的，并且收敛较快。与最小弯矩法和内力平衡法[7]相比，本文方法能实现指定目标效应的优化。本算例以关键点位移作为优化目标，在实际的工程项目中，优化目标可以包括内力、应力和位移等。

4　在大连星海湾跨海大桥中的应用

大连星海湾跨海大桥为3跨双层地锚式悬索桥， 如图8所示，加劲梁为钢桁架结构，两端设混凝土重力式锚碇。计算跨径为180 m+460 m+180 m=820 m，主桥桁架轴线宽24 m。混凝土桥塔高112 m，矢跨比1/6.6。设计时速80 km·h-1，主梁纵坡1.5%，车行道横坡1.5%，人行道向内横坡1.0%。有限元模型如图9所示。

优化目标为吊杆水平位移小于2 cm，主梁竖向位移小于5 cm，主缆跨中竖向位移小于5 cm。以上优化目标并没有严格要求为0，是为了加快收敛速度。位移值相对于主跨460 m而言，在工程上是可以被接受的。

图8　星海湾跨海桥立面布置图(单位：m)

图9　有限元模型

结构中有164段主缆和158个吊杆，经过8轮迭代，计算收敛。结构的位移和索力如图10、图11和图12所示。图10中吊杆位移为水平位移。图11和图12同时给出了文献[15]的计算结果，通过对比发现，本文计算结果和文献[15]计算结果基本一致。

图10　主梁、主缆、吊杆位移

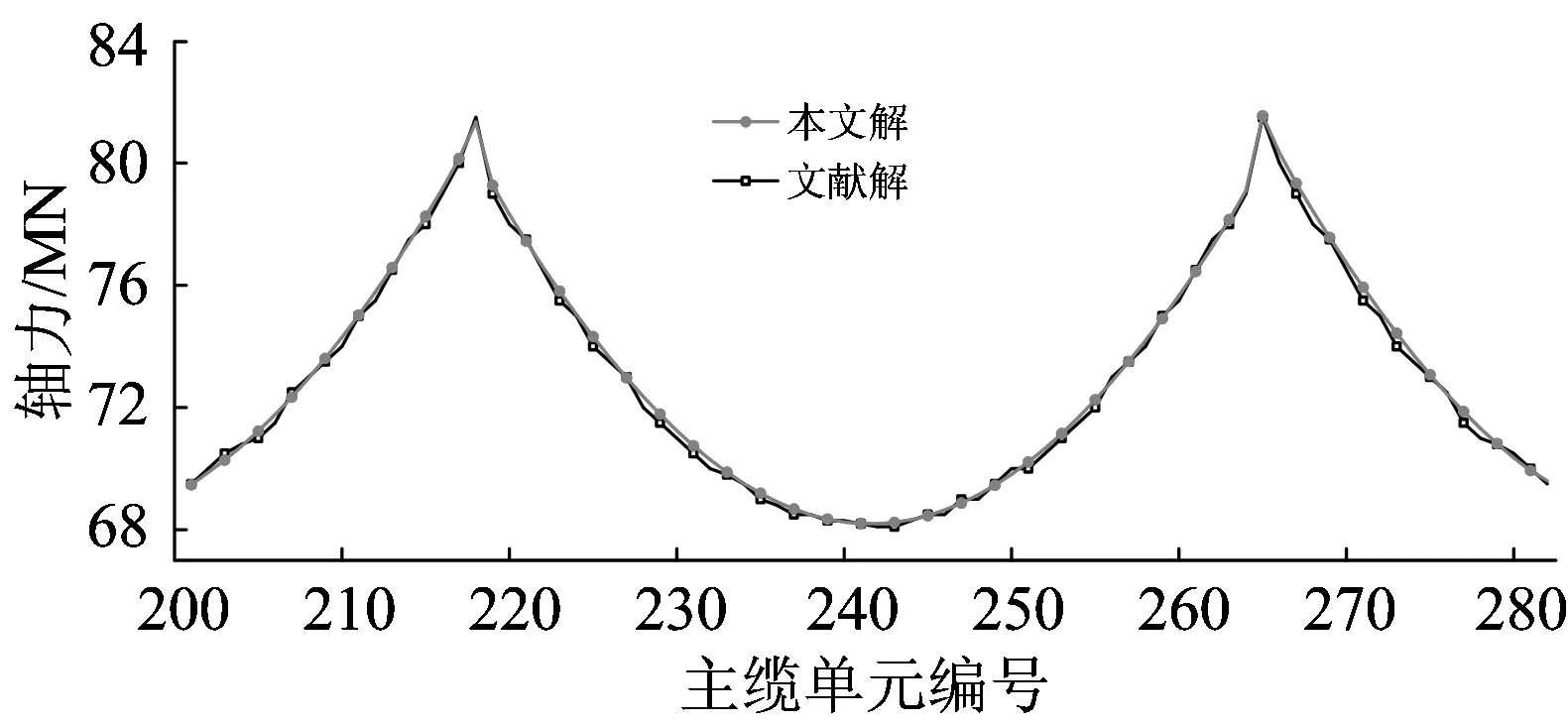
图11　主缆索力

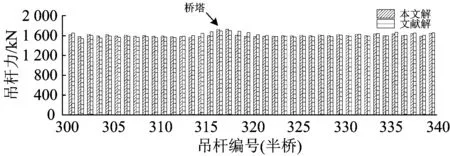
图12　吊杆索力

优化计算结果满足优化目标。在桥塔处，结构位移和索力有突变，是因为桥塔下横梁上的支座对主梁有约束作用。

5　结　语

本文提出了1种基于影响矩阵的悬索桥索力优化方法。首先在恒载和假定初始索力的作用下，形成悬索桥的初始刚度。然后在初始刚度基础上得到悬索桥的影响矩阵。最后基于影响矩阵迭代更新索力，直至收敛，得到悬索桥理想索力和合理成桥线形。本文方法应用于主跨460 m的悬索桥，经过8次迭代计算，优化计算结果为吊杆水平位移小于2 cm，主梁竖向位移小于5 cm，主缆跨中竖向位移小于5 cm，满足工程要求，并且索力计算结果与已有文献计算结果基本一致。本文方法包括悬索桥影响矩阵形成过程和索力迭代求解过程，与其他方法相比，力学概念简单，收敛较快，并能实现指定目标效应的优化。

[1]T V V， LEE H E, BUI Q T. Nonlinear Analysis of Cable Supported Structures with a Spatial Catenary Cable Element[J]. Structural Engineering and Mechanics， 2012, 43(5):583-605.

[2]KIM H K, KIM M Y. Efficient Combination of a TCUD Method and an Initial Force Method for Determining Initial Shapes of Cable-Supported Bridges[J]. International Journal of Steel Structures, 2012, 12(2):157-174.

[3]JUNG M R, MIN D J, KIM M Y. Nonlinear Analysis Methods Based on the Unstrained Element Length for Determining Initial Shaping of Suspension Bridges under Dead Loads[J]. Computers & Structures， 2013, 128(11):272-285.

[4]THAI H T, CHOI D H. Advanced Analysis of Multi-Span Suspension Bridges[J].Journal of Constructional Steel Research， 2013, 90(11):29-41.

[5]唐茂林, 强士中, 沈锐利. 悬索桥成桥主缆线形计算的分段悬链线法[J]. 铁道学报， 2003, 25(1):87-91.

(TANG Maolin, QIANG Shizhong, SHEN Ruili. Segmental Catenary Method of Calculating the Cable Curve of Suspension Bridge[J]. Journal of the China Railway Society， 2003, 25(1): 87-91. in Chinese)

[6]罗喜恒, 肖汝诚, 项海帆. 空间缆索悬索桥的主缆线形分析[J]. 同济大学学报：自然科学版， 2004, 32(10):1349-1354.

(LUO Xiheng, XIAO Rucheng, XIANG Haifan. Cable Shape Analysis of Suspension Bridge with Spatial Cables[J].Journal of Tongji University：Natural Science，2004, 32(10):1349-1354. in Chinese)

[7]王超, 檀永刚, 韩义乐. 基于ANSYS与SiPESC.OPT的自锚式悬索桥合理成桥索力优化[J]. 沈阳大学学报：自然科学版， 2013, 25(6):506-510.

(WANG Chao, TAN Yonggang， HAN Yile. Optimization of Rational Bridging Cable Force of Self-Anchored Suspension Bridge Based on ANSYS and SiPESC.OPT[J]. Journal of Shengyang University：Natural Science， 2013, 25(6):506-510. in Chinese)

[8]DAI Yuwen,WANG Youyuan. A Research to Cable Force Optimizing Calculation of Cable-Stayed Arch Bridge[J]. Procedia Engineering, 2012, 37:155-160.

[9]刘迎春. 上承式拉索组合拱桥索力优化与受力性能研究[D]. 北京: 北京工业大学, 2012.

(LIU Yingchun. Study on Cable Forces Optimization and Mechanical Behavior of Deck Type Arch Bridges with Diagonal Cables [D]. Beijing: Beijing University of Technology, 2012. in Chinese)

[10]杨俊，沈成武. 基于影响矩阵法的自锚式悬索桥施工张拉力确定[J]. 武汉理工大学学报：交通科学与工程版， 2009, 33(3):588-591.

(YANG Jun, SHEN Chengwu. Determining Construction Suspender Force of Self-Anchored Suspension Bridge on the Base of Influence Matrix[J].Journal of Wuhan University of Technology：Transportation Science & Engineering， 2009, 33(3):588-591. in Chinese)

[11]KIM H K,LEE M J,CHANG S P. Non-Linear Shape-Finding Analysis of a Self-Anchored Suspension Bridge[J]. Engineering Structures, 2002, 24:1547-1559.

[12]李黎, 陈伟, 龙晓鸿, 等. 四渡河特大悬索桥静力非线性分析[J]. 华中科技大学学报：城市科学版， 2006, 23(2):9-12.

(LI Li, CHEN Wei, LONG Xiaohong, et al. Nonlinear Static Response Analysis of Siduhe River Suspension Bridge[J]. Journal of Huazhong University of Science and Technology：Urban Science Edition， 2006, 23(2):9-12. in Chinese)

[13]张志国, 靳明君, 邹振祝. 自重荷载作用下悬索静力解析解[J]. 中国铁道科学，2004, 25(3)：67-70.

(ZHANG Zhiguo, JIN Mingjun, ZOU Zhenzhu. Static Solution of Suspension Cables under Tare Load [J]. China Railway Science，2004, 25(3)：67-70. in Chinese)

[14]GIMSING N J. Cable Supported Bridges[M]. Chichester: John Wiley, 1997.

[15]王超. 星海湾跨海大桥施工控制关键问题研究[D]. 大连: 大连理工大学, 2013.

(WANG Chao. Research on the Key Issues of Construction Control of Xinghai Bay Sea-Crossing Bridge [D]. Dalian: Dalian University of Technology, 2013. in Chinese)