有砟轨道轮轨力功率谱曲线的拟合模型
牛留斌,刘金朝,李 谷,祖宏林,杨 飞
(1.中国铁道科学研究院 基础设施检测研究所,北京 100081; 2.中国铁道科学研究院 机车车辆研究所,北京 100081)
轮轨力是运营车辆对轨道状态的动态响应,它是评价车辆运行安全的重要参数。任何影响车辆运行安全的轨道缺陷都会在轮轨力检测数据中有所反映,通过分析轮轨力检测数据、定位查找线路缺陷、消除车辆和轨道部件疲劳损伤的根源成为一种新兴的轨道检测技术[1],安装于轨道检查车上的轮轨力检测系统为获取实时轮轨力检测数据提供了技术手段。
轮轨力受到车辆及其运行速度、轨道空间状态、轮轨作用形式等多方面随机因素的影响,轮轨力的函数形式不能通过单一确定性变量表达,而应从其幅值和频率的分布特性等方面进行研究。功率谱分析方法是研究轮轨力的有效工具之一,轮轨力功率谱从幅值和频率2个方面反映了轮轨力在时域和频域的分布特征和规律。在既往轮轨力及其功率谱分布规律的研究中,轮轨力数据主要是通过车辆—轨道耦合模型的数值计算[2]、成熟商业仿真软件仿真[3]、检测系统实测[4]或者直接在特定的轨道断面上布置测试传感器[5]得到,但耦合模型或仿真模型中仿真参数的设定和轨道输入与实际轨道状态的关联程度均会制约着轮轨力计算和仿真的精度,在轨道特定位置安装传感器实测不同速度条件下轮轨力的数据量也会影响轮轨力功率谱分布特征的研究。截至目前,国内外还未建立类似于轨道不平顺谱的具有普适意义的轮轨力功率谱。
本文从有砟轨道上不同速度条件下的轮轨力检测数据时域波形重复性入手,在分析轮轨力功率谱特征分布的基础上,利用非线性最小二乘法(Nonlinear Least Squares)中的Levenberg-Marquardt算法,提出了一种结构简单、适用性强的轮轨力功率谱有理式函数拟合模型,并给出了有砟轨道轮轨力功率谱拟合结果,以验证所提拟合模型的实用性。
1 轮轨力检测数据的时域分析
本文采用的轮轨力检测数据来源于SY998799型安全综合检测车上配备的轮轨力检测系统,该检测车最高运行速度为160 km·h-1。轮轨力检测系统安装有中国铁道科学研究院研制的“单周期双桥路正弦余弦合成法”测力轮对,具有实时连续检测功能。轮轨力检测数据的采样频率为500 Hz。
图1为检测车3次以140 km·h-1速度通过中国铁道科学研究院试验场环形铁道某段200 m长有砟轨道区段时的轮轨力检测数据波形对比图。从图1可以看出:3组轮轨力检测数据的波形吻合良好,变化趋势一致,具有相似特性,反映了该区段相同轨道状态引起的轮轨力响应是相对稳定,也就是在车辆、运行速度等因素相对固定的条件下,轮轨力主要受到轨道状态的影响,相同区段轨道状态引起的轮轨力波形具有较高的相似性。
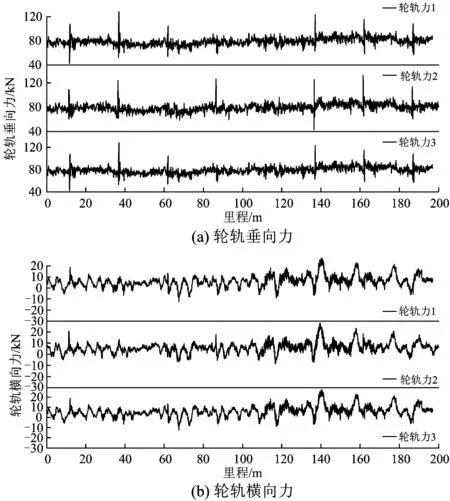
图1相同速度条件下相同区段上3组轮轨力检测数据的波形对比
图2为检测车以不同的速度通过环形铁道某段100 m长有砟轨道区段时的轮轨力检测数据波形对比图。从图2可以看出:检测车以不同速度经过同一轨道时轮轨力的波形具有很强的相似性,特别是在轮轨力波形峰值处;如图2(a)中在轨道短波不平顺引起的轮轨垂向力虽然峰值大小不相等,但轮轨垂向力峰值波形显示出同样的冲击特征,图2(b)中相同的横向轨道不平顺引起的轮轨横向力波动特征很明显,这说明了相对于固定的轨道状态,检测车对轨道的轮轨力响应特征是相对固定的,检测车运行速度的变化并不改变轮轨力波形的形状,仅会引起轮轨力波形峰值的变化。
由于低频轮轨力与测力轮对的静轮重及轨道的长波不平顺有关,且不影响轮轨力分布特征的描述,因此在下文中滤除了轮轨力检测数据中1 Hz及以下频段的低频数据成分。图3为检测车运行速度为100 km·h-1和通过环形铁道某段100 m长有砟轨道区段时25万个轮轨力样本数据分布的频数直方图及其拟合曲线。从图3可以看出:在该速度条件下,轮轨力检测数据分布的频数直方图呈现正态分布特征,其中轮轨垂向力的频数直方图拟合曲线服从0均值正态分布,而轮轨横向力的则服从正偏右拖尾正态分布。
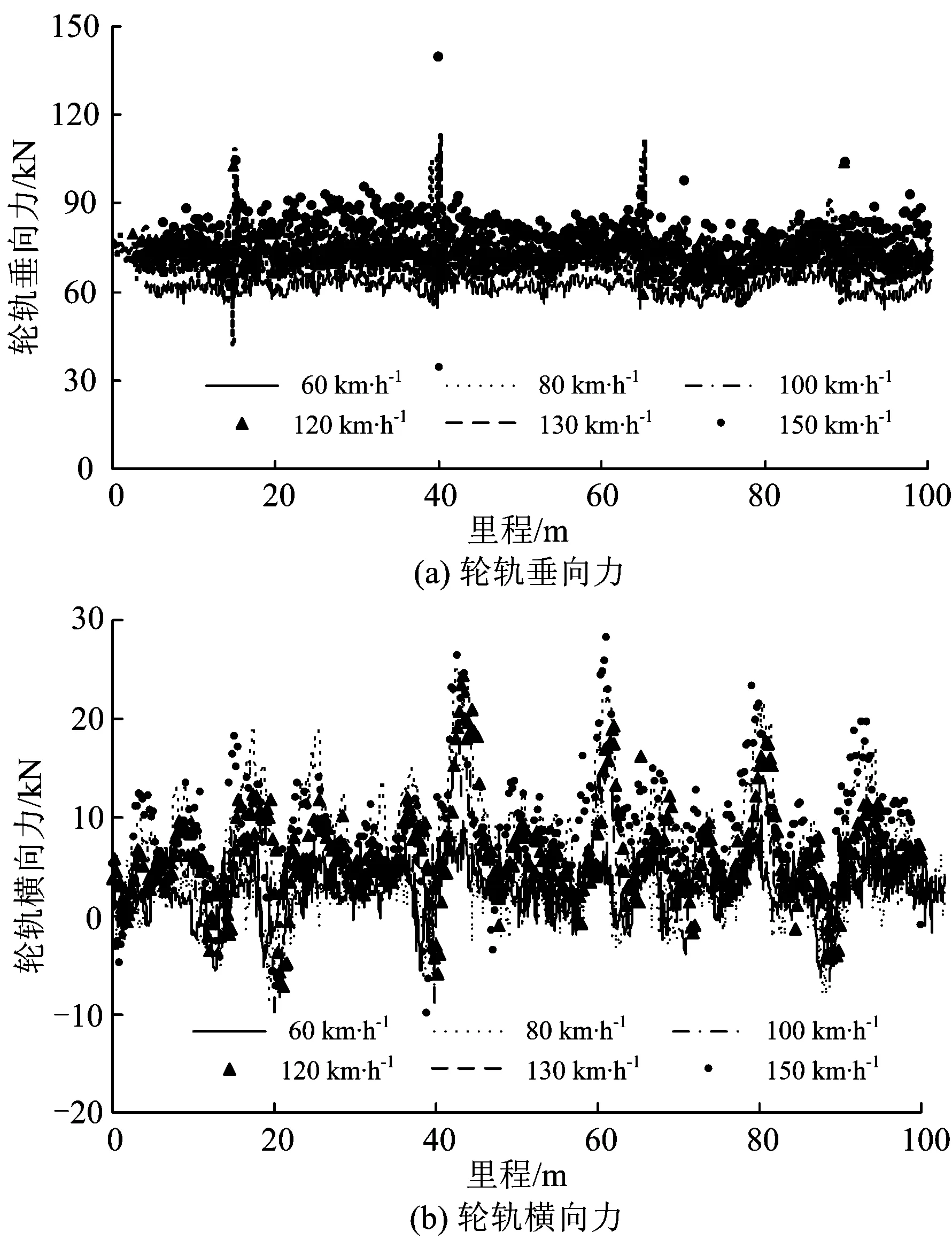
图2 不同速度条件下轮轨力检测数据的波形对比

图3100 km·h-1速度条件下轮轨力检测数据分布的直方图及拟合曲线
采用标准GB/T 4882—2001《数据的统计处理和解释 正态性检验》[6]中的非参数爱泼斯—普利(Epps-Pully)检验方法对轮轨力检测数据是否符合正态分布进行假设检验。对于n组轮轨力检测数据x的检验统计量TEP为
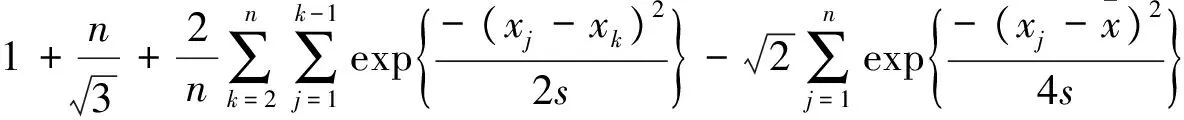
(1)
其中,
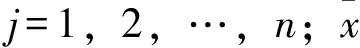
根据文献[6]查表得到由显著性水平α(如0.05)和样本量n确定的检验值Tn,如果轮轨力检测数据的检验统计量TEP大于Tn,则表示轮轨力检测数据不符合正态分布;否则,表明轮轨力检测数据符合正态分布。
本文采用的轮轨力检测数据经过Epps-Pully检验后、在显著性水平α=0.05的条件下,轮轨力检测数据的检验统计量TEP小于检验值Tn,即轮轨力检测数据符合正态分布,与图3中频数直方图拟合曲线呈正态分布的结果一致。
图4为不同速度条件下轮轨力检测数据正态分布时的概率密度曲线。从图4可以看出:随着检测车运行速度的增加,轮轨力检测数据正态分布概率密度曲线的顶峰越平缓,即曲线的峰值逐步减小;图2和图4都显示了相对于相同的轨道状态,不同速度条件下轮轨力检测数据的波形在时域上具有相似性。
功率谱分析是建立在数据平稳性假设的基础上,因此进行轮轨力检测数据平稳性检验的目的是检验该信号是否属于平稳随机过程。
平稳性检验的方法[7]有逆序检验法、游程(轮次)检验法、特征根检验法等,本文采用游程检验法进行轮轨力检测数据的平稳性检验。游程检验的步骤为:在保持随机序列原有顺序的情况下,将轮轨力检测数据分成相互排斥的2组符号序列,比如大于序列中位数的数据标记为“+”,小于中位数的标记为“-”,从而得到1组符号序列,将N1和N2分别记为符号序列内标记为“+”和“-”的个数,N为两者之和,而游程检验法中的游程定义为具有相同元素符号的序列,即把夹在异类元素符号之间的同类元素定义为1个游程。统计上述轮轨力检测数据符号序列中的游程数r。按照文献[7],平稳随机过程的游程统计量Z应近似服从标准正态分布N(0,1),即Z~N(0,1),且
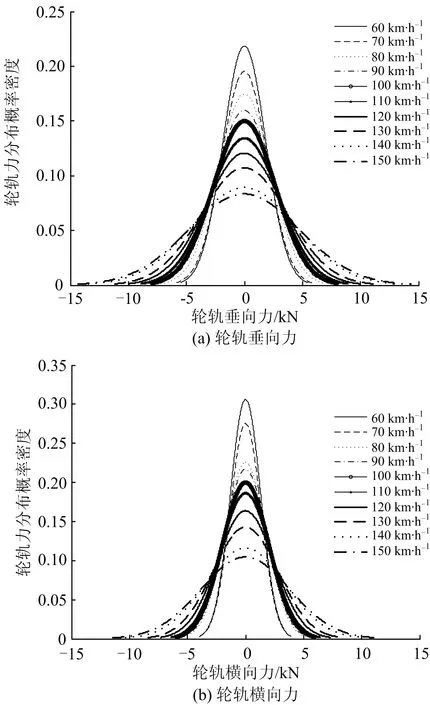
图4不同速度条件下轮轨力检测数据的概率密度分布曲线
(2)
其中,
在给定显著性水平为α的情况下,游程统计量Z落入标准正态分布N(0,1)的水平分别为1-α/2和α/2时,其由分位数u1-α/2,uα/2组成的置信区间为[u1-α/2,uα/2],则认为所检验的轮轨力检测数据属于平稳随机过程;如果游程统计量Z落入置信区间[u1-α/2,uα/2]之外,则认为轮轨力检测数据不属于平稳随机过程。
利用游程检验法对轮轨力检测数据进行平稳性检验,在显著性水平α=0.05的条件下,对应的置信区间为[-1.96,1.96],当由式(2)计算出轮轨力检测数据游程统计量Z满足|Z|<1.96时,即认为本文采用的轮轨力检测数据属于平稳随机过程。
2 轮轨力检测数据的频域分析
本文采用修正周期图谱法[8](Welch功率谱分析方法)得到轮轨力检测数据的功率谱密度曲线,Welch方法先对轮轨力检测数据分段,因相邻段内数据的重叠率为50%,傅里叶变换长度选为4 096。为了减少功率谱密度能量的泄露,在做功率谱分析时需对轮轨力检测数据进行加窗处理,本文采用加汉明窗(Hamming)进行处理。
图5为100 km·h-1速度条件下轮轨力检测数据的功率谱曲线,该数据在时域上对应的频数直方图即为图3。
从图5可以看出:轮轨力功率谱曲线包含有周期性谐波成分和随机成分;周期性谐波成分对应轮轨力功率谱曲线中的高频尖峰处,如轮轨力功率谱曲线在10,20和30 Hz等处出现规律性的尖峰值,对应的周期性谐波成分的波长分别为2.78,5.56和8.34 m等,这个周期性谐波的波长是与测力车轮的周长相关,是由车轮的不圆顺引起的;随机成分对应轮轨力功率谱中的低频成分,其变化平缓、特征明显,显示了轮轨力检测数据在频域上的变化规律。
不同速度条件下轮轨力检测数据的功率谱曲线如图6所示。从图6可以看出:在轨道状态相对稳定的条件下,由于速度的差异造成轮轨力功率谱曲线中周期性谐波成分的峰值出现的频率不一样,但是各周期性谐波成分对应的波长是一致的,即与测力车轮的周长相关;轮轨力功率谱曲线中随机成分的波形具有很强的相似性,可以通过相同的曲线模型对其进行拟合,并且在轮轨力功率谱曲线拟合前应先消除周期性谐波成分的影响。

图5100 km·h-1速度条件下轮轨力检测数据的功率谱曲线
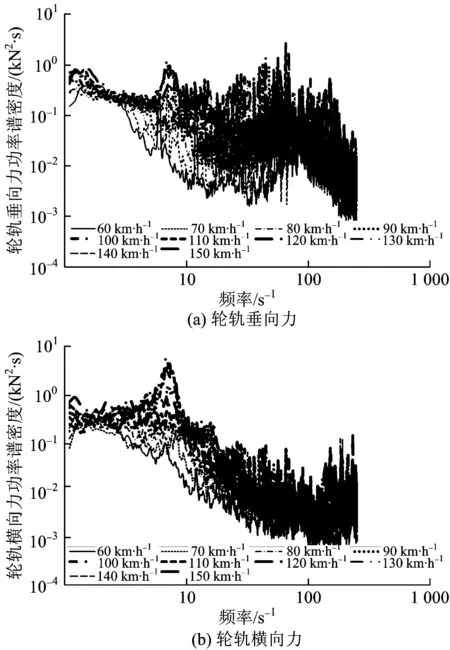
图6不同速度条件下轮轨力检测数据的功率谱密度曲线
3 轮轨力功率谱曲线拟合模型
相对于轮轨力功率谱分析,轮轨力功率谱模型的研究尚处于起步阶段,国内外鲜有实用的轮轨力功率谱模型报道。本文提出采用有理式函数得到轮轨力功率谱曲线的拟合模型(Rational Wheel-rail Force Model,RFM)。有理式函数定义为2个多项式函数相除,因此首先定义m阶多项式Fm为
Fm=F(f,p,m)=fm+p(1)fm-1+
p(2)fm-2+…+p(m)
(3)
式中:f为频率,Hz;p为由多项式函数Fm中待定系数向量,共有m个值,即p(1),p(2),…,p(m)。
经过多次拟合分析,将RFM模型的表达式定义为3阶多项式函数F3与4阶多项式函数F4的比值,即
(4)
式中:S(f,c)为轮轨力功率谱的曲线拟合模型;p3和p4分别为3阶多项式函数F3与4阶多项式函数F4中的待定系数向量,它们的长度分别为3×1和4×1;A为RFM模型的放大系数;c为RFM模型待定系数组成的向量,即由p3,p4,A组成的向量,它的长度为8×1。
由式(4)可以看出:RFM模型的待估参数少,结构简单。
本文采用非线性最小二乘法中的Levenberg-Marquardt算法估计RFM模型的待定参数c。
在进行曲线拟合前,为了使后续的曲线拟合结果能更真实地反映轮轨力功率谱的信息状态,应先对轮轨力功率谱曲线进行平滑处理,消除初始轮轨力功率谱中的周期性谐波成分和奇异点对拟合结果的影响。
3.1 平滑处理方法
本文采用五点三次平滑算法对轮轨力检测数据功率谱曲线(初始曲线)y进行平滑处理,得到用于拟合的轮轨力功率谱平滑曲线Y。五点三次平滑是一种局部加权平均的方法,算法如下。
Yi=
(5)
式中:i为轮轨力功率谱的点数,i=1,2,…,q,它的值与Welch谱分析方法中选取的傅里叶变换点数有关;yi为第i个初始轮轨力功率谱数据;Yi为第i个平滑处理后的轮轨力功率谱数据。
为了得到轮轨力功率谱平滑曲线拟合数据,以上五点三次平滑过程需要进行多次迭代。
3.2 拟合算法
通过采用非线性最小二乘拟合方法中的Levenberg-Marquardt算法对轮轨力功率谱平滑曲线Y进行拟合。该算法[9-10]是对高斯—牛顿拟合方法进行了修正的非线性优化方法,既具有高斯—牛顿法的局部收敛性,又具有梯度下降法的全局特性,它通过自适应调整阻尼因子λ达到收敛。
首先设置拟合曲线系数向量c的初始值c0(在RFM模型中,可选8个随机数据作为c0的初始值),初始权重向量h0,目标误差ξ,迭代次数M,初始阻尼因子λ0,阻尼调节因子ν(本文选择整数10)等控制参数。则当轮轨力功率谱曲线拟合到第k步时,轮轨力功率谱为Yk,拟合系数为ck,权重向量为hk,阻尼因子为λk。当k≥m时,停止迭代,输出拟合系数ck;当k 步骤1:计算第k步轮轨力功率谱拟合误差εk,即 εk=‖Yk-S(f,ck)‖ (6) 步骤2:计算系数矩阵Ck的雅克比(Jacobi)矩阵(切映射)Jk,构造增量正规方程为 (7) 其中, 式中:δ为增量正规方程的根;I为单位矩阵。 步骤3:求解增量正规方程的根δk,判断如下。 (1)若‖yk-S(k,ck)‖≥εk, 则阻尼因子为λk+1=νλk, 重新求解增量正规方程的根δk+1, 且令ck+1=ck+δk+1后返回步骤1, 并重新调整权重向量hk, 使得靠近拟合曲线的轮轨力功率谱权重大,远离拟合曲线的轮轨力功率谱数据权重小,即调整权重hk有利于消除离散边缘数据点对拟合曲线的干扰,提高曲线拟合质量。权重向量的调整方法如下。 定义经第k次迭代后的轮轨力功率谱Yk与拟合的轮轨力功率谱曲线S(f,c)之间的向量差为Dk,其加权平方和为Lk,即有 Dk=Yk-S(f,ck) (8) (9) 式中:hk,l为第l个权重向量hk的值。 销售渠道的转型升级。采用内部转化的方法,将传统的发行渠道进行扬弃,改造提升传统出版渠道,逐步提高传统渠道转化为数字渠道的比例;独立自主地建构数字产品销售渠道,建立健全个人用户、机构用户客户关系管理系统,持续推动数字出版的市场化运营和产业化发展。 (10) 其中, 式中:hk+1,l为第l个调整后权重向量hk+1的值;t为修正差值变量。 权重向量调整为hk+1后,轮轨力功率谱Yk根据各点权重的变化,生成新的轮轨力功率谱Yk+1,进行新一轮的迭代计算。 (2)若‖yk-S(k,ck)‖<εk, 且‖δk‖≥ξ, 则调整阻尼因子, 令λk+1=λk/ν,εk+1=εk, 返回步骤2,重新构造增量正规方程并求解。 (3)若‖yk-S(k,ck)‖<εk, 且‖δk‖<ξ, 令ck+1=ck+δk,进行步骤4。 步骤4:停止迭代,并将最终权重向量记为H、最终拟合系数记为C。 迭代步骤结束时,得出平滑轮轨力功率谱Y的拟合曲线S(f,C),两者的相似程度用拟合优度进行检验。 (11) 拟合优度R2的取值范围为0~1.0,R2的值越接近1.0,说明拟合效果越好。 对图5所示100 km·h-1速度条件下的轮轨力功率谱初始曲线进行五点三次平滑处理,得到其平滑曲线如图7所示。从图7可以看出:平滑处理消除了初始轮轨力功率谱数据中的奇异点及周期性谐波成分,形成规律性明显的轮轨力功率谱随机成分,它反映了轨道状态引起的轮轨力特征。 图7 轮轨力功率谱曲线平滑结果 利用RFM模型对图7中的平滑轮轨力功率谱曲线进行拟合,得到的轮轨垂向力和横向力功率谱拟合曲线的拟合优度R2分别为0.97,0.95,结果如图8所示。由图8可以看出:轮轨力功率谱平滑后,高频成分波动性较大,如200 Hz以上部分,在数据拟合过程中会影响到整体的拟合优度,在这种情况下,可以对轮轨力功率谱进行分段拟合。 图8 轮轨力功率谱拟合结果 图8中轮轨力功率谱拟合曲线与其98%置信度上、下限曲线的对比结果如图9所示。从图9可以看出:轮轨力功率谱中的随机成分大部分位于拟合曲线置信度上、下限曲线之间。 图9轮轨力功率谱拟合曲线与其98%置信度上、下限曲线的对比 同理得到图6所示不同速度条件下轮轨力功率谱的拟合曲线如图10所示,且拟合曲线的拟合优度R2均大于0.94。从图10可以看出:不同速度级下的轮轨力功率谱变化趋势相似,反映了图6中轮轨力功率谱曲线族中随机成分的变化规律。 为进一步对RFM拟合模型进行验证,利用以上拟合步骤对某条有砟轨道线路上不同速度条件下的轮轨垂向力功率谱曲线进行拟合,得到的拟合曲线(见图11)拟合优度R2均不小于0.93。 对比图10与图11可以看出:不同的有砟轨道线路状态对应的轮轨力响应状态是不同的,如图11中,该有砟轨道上轮轨垂向力功率谱曲线变化相对平缓,但同一有砟轨道线路的轮轨力功率谱拟合模型在形式上相似,均可以用RFM模型进行拟合。 图10 不同速度级轮轨力功率谱的拟合曲线 (1)有砟轨道轮轨力检测数据的时域分析结果表明:时域波形具有相似特性,车速的变化并不改变其波形的形状,仅会引起其峰值的变化;其在分布上符合正态分布,且满足平稳随机过程的检验条件;频域分析结果表明:有砟轨道线路上轮轨力的功率谱曲线包含周期性谐波成分和随机成分,周期性谐波出现的频段对应特定的空间波长且与车速有关,而轮轨力功率谱中的随机成分呈现出相似的变化规律,可用拟合模型对其进行描述。 (2)根据基于平均周期图谱分析Welch方法得到不同速度级下轮轨力功率谱的特征,提出了轮轨力功率谱曲线拟合模型(RFM),主要用于描述轮轨力功率谱中随机成分的分布规律;轮轨力功率谱中周期性谐波成分的波长主要对应车轮周长、桥梁单倍跨距等。在拟合模型中,首先采用五点三次平滑算法对轮轨力功率谱初始曲线进行平滑处理,然后采用非线性最小二乘拟合方法中的Levenberg-Marquardt算法进行拟合,最后采用拟合优度进行检验。 (3)尽管不同的有砟轨道线路对应的轮轨力功率谱分布特征不一样,但实测数据验证了本文提出的RFM拟合模型结构简单,拟合优度高,普适性强,该模型能够较好地描述有砟轨道线路轮轨力功率谱的分布状态。 (4)本文采用的轮轨力检测数据采样频率是500 Hz,轮轨力功率谱RFM拟合方法适用频段范围为1~250 Hz。由于高频轮轨力功率谱的分布离散性大,为了提高拟合曲线在全频段范围内的拟合优度,可以根据需要分频段利用RFM模型进行曲线拟合。 [1]祖宏林,张志超,汪伟. 轮轨力测量在高速铁路轨道检测中的应用研究[J].铁道机车车辆,2012,32(4):19-24. (ZU Honglin,ZHANG Zhichao,WANG Wei. Application Research of the Wheel-Rail Interaction Force Measurement on the High-Speed Railway Track Inspection [J].Railway Locomotive & Car, 2012,32(4):19-24. in Chinese) [2]冯青松,雷晓燕,练松良. 轨道随机不平顺影响下高速铁路地基动力分析模型[J].振动工程学报,2013,26(6):927-934. (FENG Qingsong,LEI Xiaoyan,LIAN Songliang. A Model of Dynamic Analysis of Ground for High-Speed Railway with Track Random Irregularities [J].Journal of Vibration Engineering,2013,26(6):927-934. in Chinese) [3]SUN Yanquan, COLIN Cole, MAKSYM Spiryagin. Study on Track Dynamic Forces Due to Rail Short-Wavelength Dip Defects Using Rail Vehicle-Track Dynamics Simulations [J]. Journal of Mechanical Science & Technology, 2013, 27(3):629-640. [4]BLANCO-Lorenzo J, SANTAMARIA J, VADILLO E G, et al. Dynamic Comparison of Different Types of Slab Track and Ballasted Track Using a Flexible Track Model [J]. Proceedings of the Institution of Mechanical Engineers Part F:Journal of Rail & Rapid Transit, 2011, 225(6):574-592. [5]王建西,许玉德,练松良,等.随机轮轨力作用下钢轨滚动接触疲劳裂纹萌生寿命预测仿真[J].铁道学报,2010,32(3):66-70. (WANG Jianxi,XU Yude, LIAN Songliang,et al. Simulation of Predicting RCF Crack Initiation Life Rails under Random Wheel-Rail Forces [J].Journal of the China Railway Society, 2010, 32(3):66-70. in Chinese) [6]全国统计方法应用标准化技术委员会. GB/T 4882—2001数据的统计处理和解释正态性检验[S].北京:中国标准出版社,2002. (National Statistical Method Application Standardization Technical Committee .GB/T 4882—2001 Statistical Interpretation of Data-Normality Tests[S].Beijing: Standards Press of China, 2002. in Chinese) [7]张树京,齐立新.时间序列分析简明教材[M].北京:清华大学出版社,2003. [8]PETRE Stoica,RANDOLPJ Moses. Spectral Analysis of Signals[M].New Jersey:Pearson Prentice Hall,2005. [9]张鸿燕,耿征.Levenberg-Marquardt算法的一种新解释[J] .计算机工程与应用,2009,45(19):5-8. (ZHANG Hongyan, GENG Zheng. Novel Interpretation for Levenberg-Marquardt Algorithm[J]. Computer Engineering and Application,2009,45(19):5-8. in Chinese) [10]MADSEN K, NIELSEN H B, TINGLEFF O. Methods for Non-Linear Least Square Problems [M]. Lyngby:Informatics and Mathematical Modelling Technical University of Denmark, DTU, 2004. [11]The Mathworks,Inc. Curve Fitting Toolbox User’s Guide[M].Natick MA:The MathWorks Inc.2010.3.3 拟合优度

4 实测数据验证

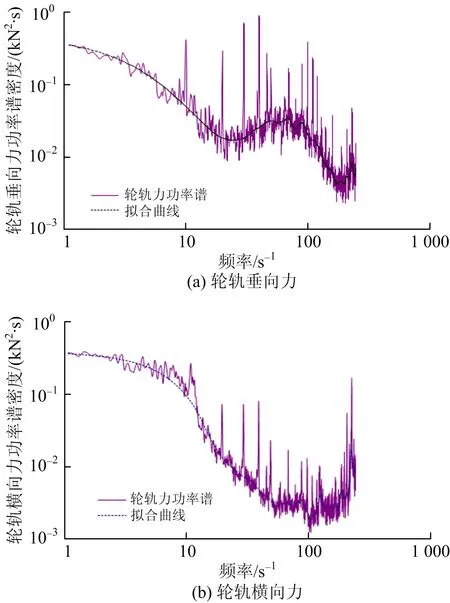

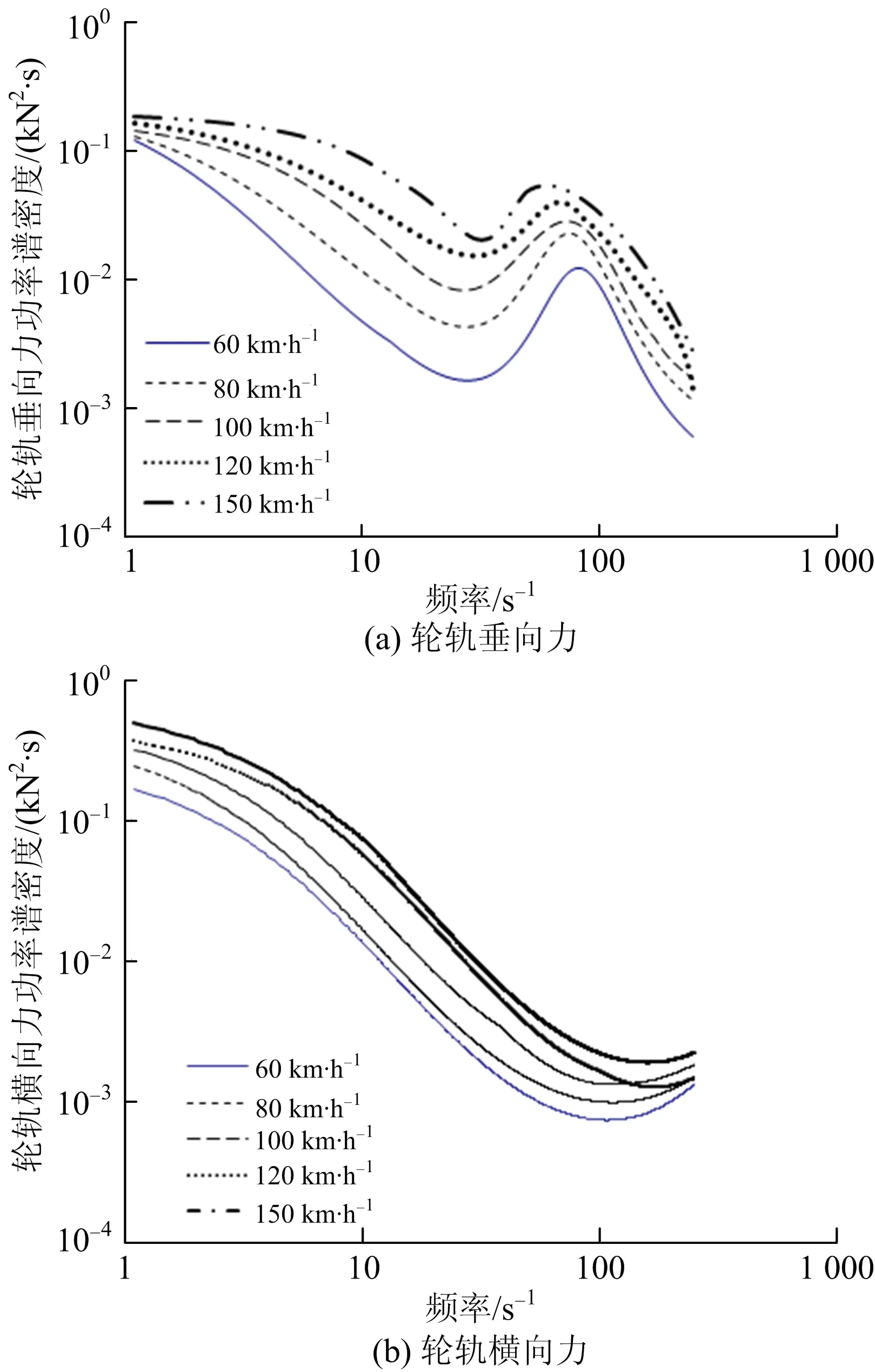
5 结 论

