高速铁路旅客出行需求集聚下的列车经停比优化方法
史 峰,李祯怡,赵 烁,单杏花
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.中国铁道科学研究院 电子计算技术研究所,北京 100081)
高速铁路列车运行组织中,列车停站方案优化是一个既重要、又复杂、且重视不够、研究积累还非常薄弱的问题。该问题的重要性表现为直接影响到旅客出行的便捷程度和出行时间的长短,直观上看,若列车停站次数越多,则旅客可搭乘的列车越多,但列车旅行时间越长,否则旅客可搭乘的列车越少,但列车旅行时间越短。其复杂性表现为每1列列车通过每个车站时都存在是否停站的0-1决策,所有列车在沿途各站是否停站的0-1决策组合构成非常庞大的离散决策空间,优化搜索的工作量极大。重视不够表现为停站优化是列车开行方案优化问题的子问题,而列车开行方案还包括列车开行径路、数量、列车等级和编组等内容,在涉及诸多重要因素的列车开行方案优化研究中,对列车开行数量、径路和列车编组更加重视,对停站方案往往只假设为几种简单的模式。研究积累还非常薄弱的原因除与前2个因素直接相关外,还由于列车停站优化问题的独立性不强,难于从整体优化问题中剥离出来。
列车停站方案优化问题的相关研究主要集中在3个方面。其一,停站方案与列车开行方案的综合优化。文献[1,2]将车站和列车都划分为3个级别,规定每个级别的列车在低级别的车站不停车、在同级别和高级别的车站全停车,并在这种固定停站模式下优化列车开行方案。文献[3,4]基于列车备选集优化列车开行方案,其中列车备选集中包括了备选列车的停站和其他信息,最终选择的所有备选列车及其开行频率确定了列车停站方案。文献[5]在列车开行方案的优化模型中包括了列车停站策略,用客流分配对包括停站方案在内的列车开行方案进行整体评价,在优化列车开行方案的同时优化停站方案。其二,列车停站方案与列车时刻表综合优化。文献[6]在列车时刻表优化问题中引入列车是否服务于O-D对的决策变量,线路上每个O-D对的服务列车数达到下限要求,目标函数中增加了列车停站总数的加权负效用,并采用列生成法求解模型。文献[7]在列车时刻表优化问题中引入列车是否在车站停车的决策变量,每个车站停车的列车数达到下限要求,停站列车在该站分配的载客能力达到该站的发送量要求,并以最小化列车停站总时间为目标函数对停站方案实现了控制。其三,给定所有列车运行径路优化停站方案。文献[8]以铁路网络为研究背景,建立了优化列车停站方案的双层规划模型,上层规划在停站数量上限约束下优化停站方案,使得广义出行费用最小化;下层规划在给定停站方案基础上进行客流分配,并采用模拟退火方法对列车停站方案进行搜索。文献[9]以列车在车站停车与否为决策变量,列车的停站数满足上下限约束,在车站停车的列车数满足下限约束,以2类列车的停站成本最小化和每个O-D对可达方案数的加权平均值最大化为优化目标,其中每类列车在车站的停车成本为固定常数,可达方案包括直达和1次换乘2种形式,可达方案数的权值按照各O-D需求所占份额确定,并利用混合遗传算法进行求解。文献[10]以列车是否在车站停车为0-1决策变量,每个车站停车的列车数满足上下限要求,线路上每个O-D对的服务列车数满足下限要求,并给出了该下限值的估计方法,以最小化所有列车的停站总数为目标,建立列车停站方案的优化模型;通过松弛0-1决策变量为连续变量求解线性规划,并按照一定的阈值进整和舍零求解模型。文献[11]针对不确定性出行需求,要求所有列车在给定车站的到发能力分别达到规定标准的置信水平条件下满足下限约束,G字头和D字头动车组在给定车站分别满足下限停站次数约束,并且共同满足上限停站次数约束条件下,谋求列车总停站数最小化。
列车在车站的停站概率简称为列车经停比。经停比描述了列车停站的疏密程度,是列车停站方案的重要属性。本文以高铁线路为背景,从最优经停比的角度研究列车停站方案优化问题。考虑到省会城市(包括直辖市)和地级市(或地区政府所在城市)高铁旅客出行需求的集聚特征,对出行需求进行分类。在省、地两级行政区内不同列车停站密度较均匀的约束下,将旅客上车时间分解为旅客出行时间偏差、列车停站时间和列车起停附加时间(简称为停站及附加时间),构建最小化人均出行时间的列车经停比优化模型,利用最优经停比可获得各需求类每个O-D对的平均服务列车数。并通过京沪高铁的实例,分析验证该优化方法的有效性。
1 列车经停比优化问题
考虑到列车经停比优化问题是列车开行方案优化问题的子问题,我们从列车开行方案优化问题出发,在若干假设条件下,提出列车经停比优化问题。
众所周知,高速铁路列车开行方案优化问题可基本描述为:给定高速铁路网络结构及线路通过能力、可支配的动车组总里程和旅客出行需求,在给定的旅客服务水平条件下,以旅客人均出行时间最少为目标,求解最优列车开行方案。
在上述列车开行方案优化问题中,高速铁路网络结构可以是单条高速铁路线路,也可以是任意网络;线路通过能力和可支配的动车组总里程共同表现为运输能力;不同O-D对的旅客出行需求在全天运营时间内具有不同的分布特征;旅客服务水平表现为列车客座利用率下限等标准。
为了简洁描述列车经停比优化问题,针对列车开行方案优化问题中的各个要素,提出如下假设条件。
(1) 仅限于高速铁路上列车经停比优化问题的研究;
(2) 对于高速铁路沿线的县、地级车站(位于县政府或地级市政府所在城市的车站),同地级市的地级车站和同省的省级车站(位于省会城市或直辖市的车站)也在这条高速铁路上;
(3) 线路上开行的列车具有相同的编组,运输能力能够满足旅客出行需求;
(4) 在运营时间内,所有O-D对不同类别的旅客出行需求都服从均匀分布;
(5) 在每条高铁线路上,列车的追踪运行间隔时间是个定值;
(6) 只考虑旅客直达出行方案(不考虑旅客换乘出行);
(7) 不同省级车站的列车经停比相互独立,每个省级车站的列车经停比独立同分布。列车在省级车站停车与否确定后,在同省的地级车站的列车经停比也独立同分布;在地级车站停车与否确定后,在同地级市的县级车站的列车经停比同样独立同分布。
现实中的高速铁路线路不一定满足假设条件(2),但只要根据相关车站客流量的大小,采用归并(到相邻省份)、升级(升级为省地级车站)或降级(降级为地县级车站)的方法进行调整,便可使假设条件(2)得到满足。
在假设条件下,如果再给定所有列车的开行径路,列车开行方案优化问题中只剩下列车停站方案没有确定。这样就可描述高铁列车经停比优化问题如下。
给定高速铁路线路、所有列车的开行径路和旅客出行需求,在假设条件的约束下,以旅客人均出行时间最小化为目标,求解最优列车经停比。
根据假设条件,只考虑旅客直达出行方案,则旅客出行时间由2部分组成,即上车时间偏差和乘车时间;其中上车时间偏差是指旅客在计划出行时间基础上推迟上车或提前上车的偏移时间;乘车时间等于列车旅行时间,而列车旅行时间包括列车区间运行时间、列车停站及附加时间。注意到列车区间运行时间是固定不变的,而在目标函数中去掉这个固定部分并不影响优化的结果,故将其忽略,所以将旅客出行时间定义为旅客上车时间偏差与列车停站及附加时间之和。
为了方便描述、求解和展示,分先后2个阶段求解省、地、县三级车站的最优列车经停比。首先,不区分地县级车站,研究省会城市高铁旅客出行需求集聚条件下的最优列车经停比;然后,在给定省级车站最优列车经停比的条件下,研究省、地2个层次需求集聚条件下地、县级车站的最优列车经停比。
2 省会城市高铁路旅客出行需求集聚条件下的列车经停比
2.1 2类车站与5类需求的划分
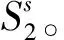
W1,1:2个不同省级车站之间的。
W1,2:省级车站与外省地县级车站之间的。
W2,2:不同省的2个地县级车站之间的。

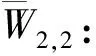
上述需求类的符号中,没有上画线的表示省际高铁旅客出行需求类,有上画线的表示省内高铁旅客出行需求类;下标1和2分别表示省级车站和地县级车站。在下文的客流量比例、O-D起讫站同时停站概率、通过O-D对的列车数、人均上车时间偏差等参数或变量中,都采用相同的命名规则。
2.2 各需求类每个O-D对的平均服务列车数

(1)

(2)
其中,通过O-D对的列车是指同时通过O-D对起讫站的列车,服务于O-D的列车是指同时在O-D对起讫站停车的列车。
2.3 人均出行时间
1)旅客人均上车时间偏差

(3)
式中:T为全天运营时长,h。
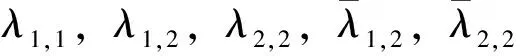
Tdiff=λ1,1Tdiff,1,1+λ1,2Tdiff,1,2+λ2,2Tdiff,2,2+
(4)
2)旅客人均停站及附加时间
旅客人均停站及附加时间Tstop等于人均中途停站数与每次停车的平均停站及附加时间τstop之积,而旅客人均中途停站数又等于旅客中途人均通过车站数与列车在任意车站的平均经停比之积。
旅客中途人均通过车站数不包括旅客上下车的车站,比旅客中途人均通过的区间数少1。而区间数等于旅客人均行程l除以高铁线路的平均站间距d,所以旅客中途人均通过车站数等于1/d-1。根据两类车站所占的比例θ1,θ2和列车在两类车站的经停比x1,x21及x22,可得列车在任意车站的平均经停比等于θ1x1+θ2[x1x21+(1-x1)x22]。所以有

(1-x1)x22)]τstop
(5)
2.4 省会城市高铁旅客出行需求集聚下的最优列车经停比优化模型
在不同的高铁线路上,尽管通过能力都能满足需求,但运行图的铺画结果与通过能力紧张程度是相关的,通过能力越紧张,要求不同列车的旅行速度越接近,进而要求不同列车的停站密度越接近,也就是说,要求在省级车站停车条件下的列车经停比x21与不停车条件下的列车经停比x22达到某种规定的比值,可表示为x22=αx21,其中,α(α>0)用于描述不同条件下列车停站密度的接近程度,α的值可以依据运行图统计获得。
综上所述,以旅客人均出行时间最少为目标函数,构建省会城市高铁旅客出行需求集聚下的最优列车经停比优化模型M为
minZ=Tdiff+Tstop
(6)
s.t.
x22+αx21
(7)
x1>0;x21≤1
(8)

2.5 省会城市高铁旅客出行需求集聚下的实例分析


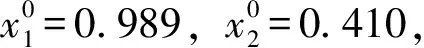
|Z*-Z0|=|0.605-0.620|
=0.015(h)=0.9(min)
由图1可以看出:随着列车经停比的增加,人均旅行时间在前面下降期下降的速度较快、而在后面增长期增加的速度较慢。高铁运营企业可据此在最优列车经停比基础上适度增加列车经停比,用少量的人均旅行时间增量换取更多的服务列车。与省级车站相比,地县级车站列车经停比从最优列车经停比开始,沿着列车经停比增加方向,人均旅行时间增长速度更快。这是因为地县级车站数比省级车站数更多一些所致。

图1不区分地县级站条件下随列车经停比变化的人均出行时间等值线
与地级车站相比,县级车站的列车经停比增加时,人均旅行时间在前期降低的更快,在后期增长的更慢。这是因为京沪高铁沿途的县级车站数所占比例较少所致。
在省会城市高铁出行高度集聚状态下,省级车站的最优列车经停比几乎为1,可以为省级车站相关需求提供更多的服务列车数。这个实例的分析结果与高铁现场组织形式是完全契合的。
3 两层次高铁旅客出行需求集聚下的列车经停比
3.1 3类车站与13类需求的划分
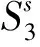
将全体高铁旅客出行需求O-D对集划分为6个省际需求类(其表示符号不带上画线者)和7个省内需求类,其中省内需求类包括地县级车站都隶属同1个地级市的4个需求类(其表示符号带有单上画线者),地县级车站隶属不同地级市的3个需求类(其表示符号带有双上画线者)。表示符号下标中的1,2,3分别对应表示省级车站、地级车站和县级车站。具体13个双向旅客出行需求类如下。
W1,1:2个不同省级车站之间的。
W1,2:省级车站与外省所辖地级车站之间的。
W1,3:省级车站与外省所辖县级车站之间的。
W2,2:不同省的2个地级车站之间的。
W2,3:地级车站与外省县级车站之间的。
W3,3:不同省的2个县级车站之间的。


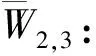


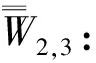
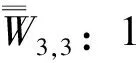
3.2 两层次高铁旅客出行需求集聚条件下的最优列车经停比优化模型

(9)
由所有开行列车的径路统计获得各需求类每个O-D对的平均通过列车数,分别记为

(10)
类似于式(2),由式(9)和式(10)可得各需求类每个O-D对的平均服务列车数分别为

(11)
类似于式(4)可得旅客人均上车时间偏差为

(12)
类似于式(5)可得旅客人均停站及附加时间为

(13)

(14)
s.t.
x3,2=βx3,1
(15)
x2>0;x31≤1
(16)
模型中的约束条件式(15)描述了在地级车站停车和不停车2种条件下列车经停比应满足规定的比例要求,β(β>0)用于限制不同列车具有相近的旅行速度,描述了不同条件下列车停站密度的相近程度,β可以依据运行图统计获得。

3.3 两层次高铁旅客出行需求集聚条件下的实例分析
仍然以京沪高铁为例,京沪高铁省、地、县3类车站数所占比例分别为θ1=0.173 9,θ2=0.652 2,θ3=0.173 9,各个需求类客流量所占比例分别为
λ1,1=0.299 4,λ1,2=0.309 6,
λ1,3=0.063 6,λ2,2=0.061 4,
λ2,3=0.006 0,λ3,3=0.000 1,
各需求类每个O-D对的平均通过列车数分别为
m1,1=65.58,m1,2=67.14,m1,3=67.04,
m2,2=69.96,m2,3=63.79,m3,3=63.83,
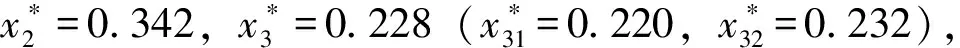
随着列车在地、县级车站经停比(x2,x3)的变化,人均出行时间的等值线如图2所示。由图2可以看出:随着列车经停比的增加,人均旅行时间在前面的下降期降速较快、而在后面的增长期增速较慢。最优解临近等值线类似于水平椭圆状表明:与地级车站相比,县级车站的列车经停比从最优列车经停比开始,沿着列车经停比增加方向,人均旅行时间增长速度更慢。这是因为京沪高铁线上县级车站数所占比例较少所致。
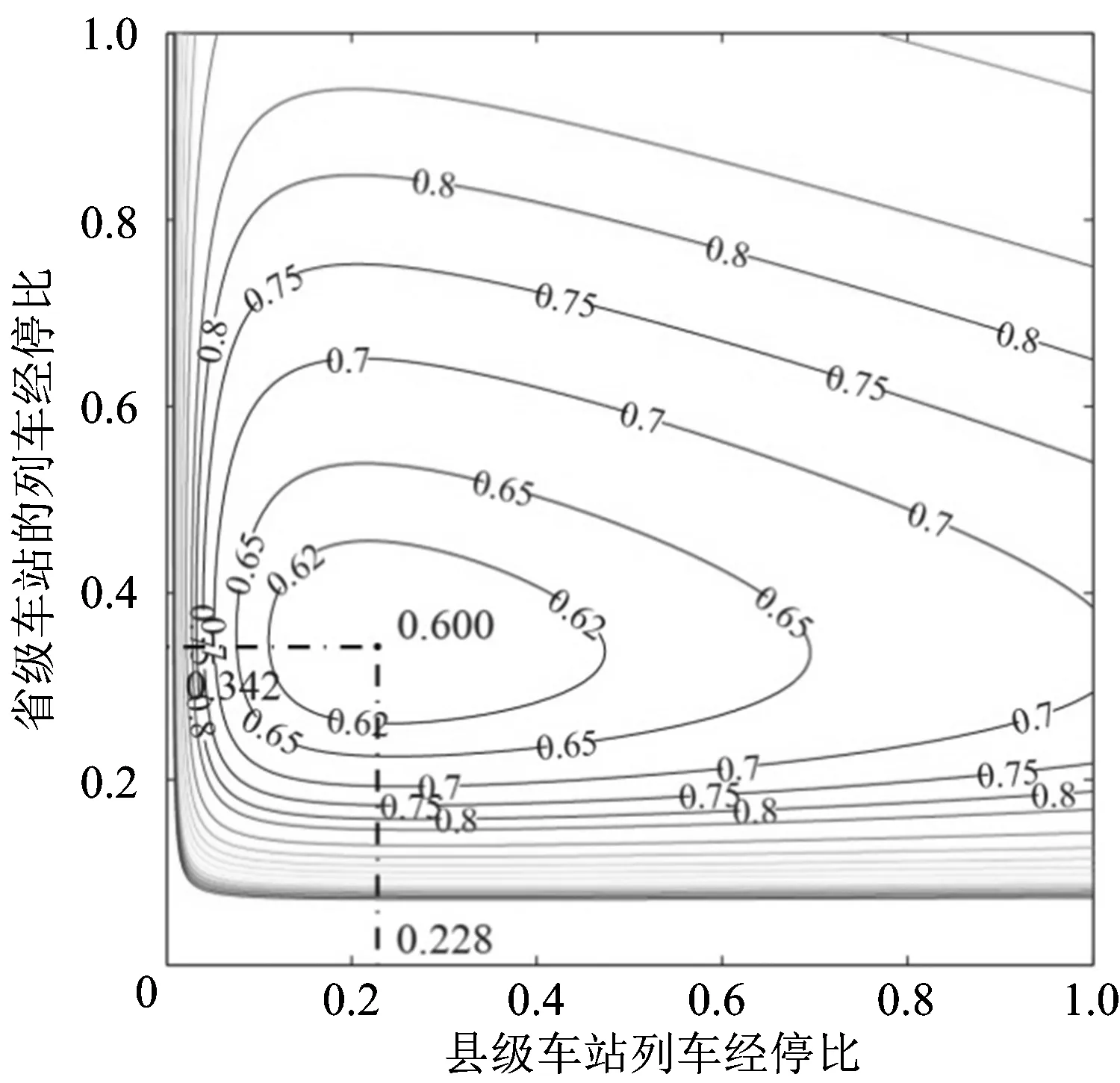
图2 省级车站的列车经停比为1时人均出行时间等值线
重要的是,我们可以利用最优列车经停比和式(11)计算出服务各个需求类的列车数分别为
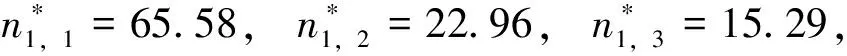
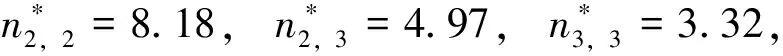


=0.011(h)=0.66(min)
模型最优列车经停比与实际列车经停比的相对偏差为
由此可见,实际列车经停比与模型最优列车经停比的偏差非常小。
各个需求类的实际服务列车数为



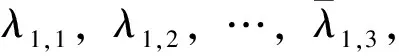
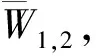
当然,由于本文给出的最优列车经停比研究方法需要满足前提假设条件(1)—(7),而生产实际中难以完全具备这些假设条件,所以生产实际中的列车经停比略高于模型的最优列车经停比也是合理的,旅客多支付少量人均出行时间,但能获得更多的服务列车。
另外,由于京沪高铁的县级车站数所占比例特别少(θ3=0.173 9),所以地级车站的需求集聚特征非常弱,这也是β=1/0.95>1的原因。
对京广高铁和杭福深高铁的列车经停比进行了优化计算也获得相近的计算结果,将2个层次的优化问题进行整体优化,同样获得了相同的结果。本文篇幅所限未予列出。
4 结 论
(1)列车在省、地级车站停与不停2种条件下,在所辖行政区内列车经停比是控制列车停站均匀程度的参数,该参数值与线路能力的富足程度相关,与对应行政区所辖的地、县级车站数相关。
(2)在省、地两级行政区内各列车停站密度较均匀的约束下,以最小化旅客人均出行时间为优化目标,建立列车经停比优化模型。虽然理想化假设可能导致列车最优经停比略小于实际的列车经停比,但优化结果与实际情况偏差很小,验证了该优化方法的合理性。
(3)省级车站的最优列车经停比接近于1,说明省级车站具有显著的高铁旅客出行需求集聚特征;如果县级车站数所占比例较大,则地级车站也具有一定的集聚特征;县级车站的列车经停比相对稳定,是因为县级车站没有大量旅客集聚需求的支撑。
(4)不论哪一类车站,随着列车经停比增加,人均旅行时间在前面的下降期下降速度较快、后面的增长期速度增长较慢。高铁运营企业可据此在最优列车经停比基础上适度增加列车经停比,用少量的人均旅行时间增量换取更多的服务列车。对于数量占比越小的车站类别,从最优列车经停比开始,在列车经停比增加方向,人均旅行时间的增长速度越慢。
[1]GOOSSENS J W, KROON L. A Branch-and-Cut Approach for Solving Railway Line-Planning Problems[J]. Transportation Science, 2001, 38(3):379-393.
[2]GOOSSENS J W, HOESEL S V, KROON L. On Solving Multi-Type Railway Line Planning Problems[J]. European Journal of Operational Research, 2006, 168(2):403-424.
[3]FU H, NIE L, MENG L, et al. A Hierarchical Line Planning Approach for a Large-Scale High Speed Rail Network: the China Case[J]. Transportation Research Part A Policy & Practice, 2015, 75:61-83.
[4]苏焕银, 史峰, 邓连波,等. 面向时变需求的高速铁路列车开行方案优化方法[J]. 交通运输工程与信息, 2016,16(5):110-116.
(SU Huanyin, SHI Feng, DENG Lianbo, et al. Time-Dependent Demand Oriented Line Planning Optimization for the High-Speed Railway[J]. Journal of Transportation Systems Engineering and Information Technology,2016,16(5):110-116.in Chinese)
[5]史峰,邓连波,霍亮. 旅客列车开行方案的双层规划模型和算法[J]. 中国铁道科学, 2007, 28(3):110-116.
(SHI Feng, DENG Lianbo, HUO Liang. Bi-Level Programming Model and Algorithm of Passenger Train Operation Plan[J]. China Railway Science, 2007,28(3):110-116.in Chinese)
[6]YUE Y, WANG S, ZHOU L, et al. Optimizing Train Stopping Patterns and Schedules for High-Speed Passenger Rail Corridors[J]. Transportation Research Part C Emerging Technologies, 2016, 63(2):126-146.
[7]YANG L, QI J, LI S, et al. Collaborative Optimization for Train Scheduling and Train Stop Planning on High-Speed Railways[J]. Omega, 2016, 64:57-76.
[8]邓连波, 史峰, 周文梁. 旅客列车停站设置方案优化[J]. 中国铁道科学, 2009,30(4):102-107.
(DENG Lianbo, SHI Feng, ZHOU Wenliang. Stop Schedule Plan Optimization for Passenger Train[J].China Railway Science,2009,30(4):102-107.in Chinese)
[9]CHEN Dingjun, NI Shaoqun, XU Chang’an, et al. High-Speed Train Stop-Schedule Optimization Based on Passenger Travel Convenience[J]. Mathematical Problems in Engineering, 2016(3):1-10.
[10]李得伟, 韩宝明, 李晓娟,等. 基于节点服务的高速铁路列车停站方案优化模型[J]. 铁道学报, 2013, 35(6):1-5.
(LI Dewei, HAN Baoming, LI Xiaojuan, et al.High-Speed Railway Stopping Schedule Optimization Model Based on Node Service[J]. Journal of the China Railway Society,2013,35(6):1-5.in Chinese)
[11]牛丰, 戚建国, 秦进. 基于不确定客流的高速铁路列车停站方案优化方法[J]. 铁道学报,2016, 38(7):1-7.
(NIU Feng, QI Jianguo, QIN Jin. Optimization Model for Train Stopping Plan on High-Speed Railway Corridor with Uncertain Passenger Demands[J].Journal of the China Railway Society,2016,38(7):1-7.in Chinese)
[12]甄静. 京沪线铁路客流规律分析[J]. 中国铁道科学, 2002,23(2):122-126.
(ZHEN Jing. Analysis of the Rule of Passenger Traffic Flow of Jing-Hu Railway Line[J]. China Railway Science, 2002,23(2):122-126.in Chinese)
[13]兰淑梅, 赵映莲, 汤奇志. 论京沪高速铁路客流及其组织方案[J]. 中国铁道科学, 2002, 23(3):124-129.
(LAN Shumei, ZHAO Yinglian, TANG Qizhi. Passenger Flow and Its Organization Solution for Beijing-Shanghai High-Speed Railway[J]. China Railway Science, 2002, 23(3):124-129.in Chinese)

