知识团视角下中美高中数学教材的比较研究
孙成成+胡典顺
摘 要 通过比较不同版本教材中的数学知识团,可以帮助教师理清知识脉络、明确知识点之间的联系、促进教学设计的改进,并有利于学生对数学知识的系统化掌握。选取“人教A版”和“核心教材”为研究对象,以圆锥曲线知识团的建构为例,对中美高中数学教材知识团的建构特征进行比较分析发现,两套教材在知识团特征、辅助知识团建构方式和知识团习题这几个层面上存在一定的差异。因此,教师需要深刻地研究和掌握知识团的内涵;学会驾驭教材并挖掘隐性知识点;重视研究性题型的开发。
关键词 知识团 圆锥曲线 中美数学教材 比较研究
一、研究背景
教材研究与建设一直是课程与教学研究中的核心问题,也是教学质量提升、教学改革实施的基本保障。教材研究也是中小学一线教师在教学实践中普遍关心与经常研究的一个问题[1]。很多研究是从宏观层面上去分析一本教材或一章教学内容,少有研究者去研究一个特定数学内容概念化、结构化的呈现方式。简单的对比并不能揭示出一个特定内容的数学本质及其与其他内容的关联,而从微观层面上去分析,却可以获得其概念化、结构化的特征[2]。史宁中教授提到的知识团概念,为学者更深入更微观地研究中学数学内容提供了方向。
在中学数学中,知识是层层深入、逐渐递进而又紧密联系的。然而实际教学中,由于缺乏对知识团结构的把握,对知识点间的联系不够明确,一些教师往往只会依据教学大纲和教材对知识点进行线性讲解,导致教学过程中的清晰度不够高,降低了学生对数学知识结构的掌握。高中圆锥曲线知识点复杂并且知识点间联系紧密,为了更好地认识中学数学教材知识点的设计,通过中、美两国教材中圆锥曲线知识团建构的比较,来帮助教师理清知识点结构和知识点网络,了解数学知识团的属性和规律,为更好地设计教学、提高数学课堂教学质量提供新思路。研究选取了Core-Plus Mathematics(Preparation for Calculus,Student Edition PartB,2010年版)(以下简称“核心教材”)和中国的《普通高中课程标准实验教科书数学A版》(以下简称“人教A版”)。
二、研究准备
1.知识团的概念
在数学中知识点可以分为数学概念和数学命题。数学概念是现实世界中空间形式和数量关系及其本质属性在人们头脑中的反映,数学命题是用来表示数学判断的语句或符号的组合。知识点所包含的数学概念与数学命题在学生接触之前或是模糊的或是新的或是未曾在大脑中建构起来的。若干知识点构成一个知识团。知识团的选取与确立需要遵循两个原则:知识团的容量应尽可能小;若兩个知识点之间有必然的不可拆分的逻辑关联,则这两个知识点同属于一个知识团[3]。
2.分析和统计框架的建构
(1)知识团特征
知识团的广度是指一个知识团所含知识点的多少;知识团的深度即概念和命题的深度之和[3]。概念的深度主要分为“白描、归纳总结、抽象定义”三个水平,分别赋值1、2、3。其中,通过画出图形并指出这种图形就是某个概念的定义形式属于白描层次;通过发现规律、推导、证明、归纳总结得出概念的定义形式属于归纳总结层次;直接给出概念的定义形式属于抽象定义。命题的深度主要分为“了解、理解、应用”三个水平,分别赋值1、2、3。其中,直接给出结论的命题属于了解层次;通过证明或归纳总结而给出的命题属于理解层次;在理解层次的基础上运用于衍生或引出其他知识点的命题属于应用层次。本研究的知识点包括显性概念和隐性概念、显性命题和隐性命题。将教材中用特殊符号、特殊颜色或特殊字体标记的概念(或命题)作为显性概念(或显性命题),将教材中没有用特殊符号、特殊颜色或特殊字体标记但却是教学重点或难点并能揭示知识团本质属性的概念(或命题)作为隐性概念(或隐性命题)。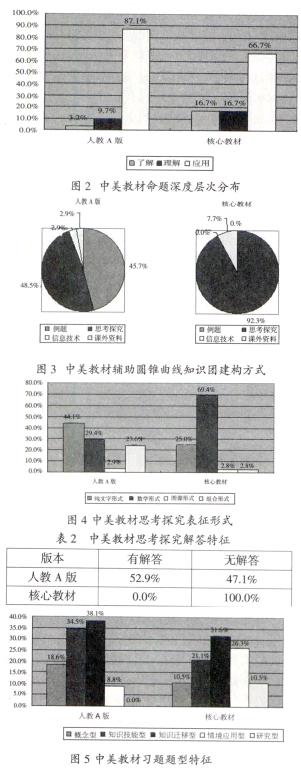
(2)辅助知识团建构的方式
教材中为引入知识点或加深知识点的理解和掌握而呈现出来的教学方法或学习资料等都属于辅助知识团建构的方式,主要包括例题、信息技术、课外资料和思考探究。以“例1、例2…”这种形式呈现的属于例题;呈现出运用信息技术画图或介绍知识点的属于信息技术;呈现出数学知识在生活或科学中运用的事例的属于课外资料;“人教A版”中标有“思考”“观察”“探究”栏目的属于思考探究方式,并且每一个栏目算作一个思考探究题。“核心教材”中调研之下的题目属于思考探究方式,并且每一个以小写字母为题号的算作一个思考探究题。教材中的思考探究主要以4种形式呈现:第一种纯文字形式,思考探究问题的主干完全是由文字表述;第二种数学形式,思考探究问题的主干是由文字和数学符号或数学表达式共同表述;第三种图像形式,思考探究问题的主干是由文字和图像共同表述;第四种组合形式,思考探究问题的主干呈现出上述三种表述形式。
(3)知识团习题
习题有大题与小题之分,我们把含有关联密切的多问的习题算作一道题,包含多道小题的习题算作一道题。习题的统计是对教材每一节或每一调研之后习题的统计,不包括对本章复习或本单元复习题目的统计。知识团习题题型包括概念型、知识技能型、知识迁移型、情境应用型和研究型。其中,知识点只涉及概念并且用于加强概念记忆和理解的习题属于概念型;以圆锥曲线知识团为主干,训练学生命题与概念综合运用能力的习题属于知识技能型;以圆锥曲线知识团和其他类型知识团共同为主干的习题属于知识迁移型;运用信息技术解题或以生活、科学为背景的习题属于情境应用型;在小组讨论、搜集资料、实验操作、写总结或论文、作报告中,至少包含两种形式以上的习题属于研究型。
三、中美数学教材圆锥曲线知识团建构的比较分析
1.中美数学教材圆锥曲线知识团的比较分析
(1)圆锥曲线知识团特征的比较分析
表1反映出,在圆锥曲线知识团中,“人教A版”的显性概念数比“核心教材”的多,但是“人教A版”与“核心教材”的隐性概念的数目都很少并且都是2。“人教A版”与“核心教材”都不含有显性命题,但是“人教A版”的隐性命题数是“核心教材”的5倍。“人教A版”在这一知识团的广度是“核心教材”的2倍多,深度也是“核心教材”的将近2倍。
(2)圆锥曲线知识团概念深度层次的比较分析
图1表明,在圆锥曲线知识团中,“核心教材”比“人教A版”更加重视抽象定义这个层次,它在“核心教材”中所占的比例最重,为77.3%;而“人教A版”概念的抽象定义这一层次所占比例是最少的,只有17.7%。从整体上看,“人教A版”概念深度层次分布呈现出递减的趋势,抽象定义这一层次所占比重最小,而“核心教材”概念深度层次分布呈现“U型”,归纳类比层次所占比重最小。
(3)圆锥曲线知识团命题深度层次的比较分析
图2表明,在圆锥曲线知识团中,“人教A版”和“核心教材”都非常重视数学命题的应用,但是“核心教材”在了解和理解两个层次上的比重都比“人教A版”的多,并且比重分布也比“人教A版”相对均衡。而“人教A版”在命题应用上的比重比“核心教材”的多,但在了解这个层次上的比重极少,只有3.2%。
2.中美数学教材辅助圆锥曲线知识团建构的比较分析
(1)中美教材辅助圆锥曲线知识团建构的方式的比较
图3表明,“人教A版”中通过例题、思考研究、信息技术和课外资料四种方式来辅助圆锥曲线知识团的建构,而“核心教材”只有思考研究和课外资料两种方式。“人教A版”是以例题和思考探究两种方式为主干,并且思考探究的比重偏多,而“核心教材”是以思考探究为主干并且是贯穿整个教材。
(2)中美数学教材圆锥曲线知识团思考探究表征形式的比较
图4反映出,在圆锥曲线知识团思考探究表征形式中,纯文字形式在“人教A版”中所占的比重最大,而数学形式在“核心教材”中所占的比重最大。图像形式在“人教A版”和“核心教材”中所占的比重都是最小的,都不超过3%。从组合形式上看,“人教A版”是“核心教材”的8倍。
(3)中美数学教材圆锥曲线知识团思考探究解答特征的比较
表2反映出,在圆锥曲线知识团中,“人教A版”的思考探究有超过一半是给出解答的,而“核心教材”中所有的思考探究都没有给出解答。
3.中美数学教材圆锥曲线知识团习题的比较分析
图5反映出,在圆锥曲线知识团习题中,“人教A版”中概念型和知识技能型的习题所占的比重都比“核心教材”的大。而“核心教材”中情境應用型习题所占的比重是“人教A版”的将近3倍;“核心教材”中研究型习题占10.5%,而“人教A版”中却没有研究型习题。从整体上看,“人教A版”和“核心教材”圆锥曲线知识团习题分布都呈现“倒U型”,即知识迁移型习题的比重都是最大的,但“核心教材”中习题题型的分布更均衡。
四、启示
1.知识团内涵的进一步理解
史宁中教授指出,两个知识点之间有必然的不可拆分的逻辑关联,则这两个知识点同属于一个知识团。这里的不可拆分性是相对不可拆分性,即知识团中的知识点在揭示同一个特定的数学属性时,这两个知识点之间是不可拆分的。例如,椭圆的概念和双曲线的概念这两个知识点都能够揭示圆锥曲线的本质属性,具有不可拆分性也具有必然的联系,属于同一个知识团。然而,在揭示椭圆的本质属性时,椭圆的概念与双曲线的概念之间就不具备不可拆分性。这也意味着知识团具有生成性,如果两个知识团的知识点合在一起可以揭示另一种特定的数学属性,并且这些知识点之间具有必然的不可拆分的联系,那么这些知识点就组成了一个新的知识团,而原知识团就是新构知识团的子团。
知识团的建构也是数学认知结构的一种建构。认知结构是学习者头脑里的知识结构,是学习者观念的全部内容和组织。数学认知结构是学习者通过教师所激发起来的心理结构作用于外界的数学知识结构而形成的一种内在的知识结构。教师要为学生建构良好的知识脉络,就要理清知识之间的联系,对教材上的知识点进行剖析、加工和重新组织,这就需要建立良好的知识团体系。所以在知识团建构的过程中,既要重视数学知识发生的顺序性和阶段性以及学生的认知发展水平,又要重视对知识点、知识团的整合。在“人教A版”的圆锥曲线知识团里,知识点之间出现了“断层”的现象,例如圆锥曲线中的圆放在了必修2,而椭圆、双曲线和抛物线放在了选修2-1,在选修4-4还涉及到了一些圆锥曲线的参数方程。所以数学教师应当了解知识团的未完成性、重塑性和生成性等特点,意识到知识团是数学思维的架构能力的体现,明确如何在教学中不断充实知识团以及如何从知识点过度到知识团、再从知识团细化到知识点。
2.驾驭教材,挖掘隐性知识点
构建良好知识团的前提是要正确引起学生进行积极深刻的思考进而产生“头脑风暴”。在“人教A版”中促进学生思考比较常见的方式是,在知识点附近采用“思考”或“探究”栏目并以旁注的形式呈现出问题来启发思考,促进对知识点的掌握。但是往往在这些栏目的后面直接就会给出思考的答案或探究的结果。而在“核心教材”中,思考探究贯穿整个教材,但教材并没有给出明确的思考解答或探究结果,甚至一些知识点是在思考探究的过程中给出的。“核心教材”这样设定的目的是让学生自己去发现问题、提出问题、思考问题、解决问题,进而获得知识点。任何有效的学习都是一个主动建构的过程,教师必须调动学生的主观能动性,引导学生通过自己积极主动的思维活动来学习数学、获取知识[4]。而“人教A版”把所要思考探究的答案以书面形式呈现在学生的面前,这不利于调动学生学习的积极性,也会阻碍学生的独立思考、影响学生的创造性思维、个性思维以及独特性思维的发展。所以,“人教A版”可以对思考探究的解答进行适当的修改,应当着力于培养学生放下教材去思考和探究的能力。
“人教A版”中有些没有特殊标记的命题,些没有特殊标记但却是教学的重点或难点的命题都应当是知识点,教师要学会挖掘和整理教材中的隐性知识点,也要教授学生挖掘隐性知识点的方法。在“核心教材”中,辅助圆锥曲线知识团建构的方式只有思考探究和课外资料,这就要求数学教师在传授知识的过程中要有自己的方法,不能照本宣科,而要根据实际情况填补教材的不足,并明确是教师引导学生而非教材在引导学生。
3.加强研究性题型的开发
知识树能使错综复杂的知识内容条理化、系统化,使各种关系变得明确直观[5]。知识团的迁移应用就可以形成知识树,可以清楚地看到各个相对独立的知识团,也可以清晰地展现出各知识团之间的相互联系。“核心教材”最大的特色在于每一调研里都会设置一些研究性题目,这些题目都需要知識团的迁移应用,并且一般都分为三个阶段来完成。第一阶段是问题阶段,需要学生从多个角度认识和分析问题并确定研究方案;第二阶段是求解阶段,主要包括搜集和研究信息资料、调查研究、建立数学模型、交流研讨等;第三阶段是表达内化阶段,主要是学生将取得的进展进行归纳整理、总结提炼,形成书面材料。研究性题型重过程、重应用、重体验、重全员参与,帮助学生获得亲身参与研究与探索的体验、学会与人沟通和合作、增强探究创新意识、了解科学研究和学习方法、加快知识团的稳固建构。我国数学课标强调现代数学教学不仅注重学生的数学学习水平和学习结果,还要注重他们的学习过程以及在数学活动中所表现出来的情感、态度和价值,让他们更好地认识自我,实现全面发展。所以缺乏研究性练习设置的“人教A版”应当借鉴“核心教材”的方式,加大研究性题型的开发,促进学生数学素养的全面提高。
参考资料
[1] 吴立宝,曹一鸣.中学数学教材的分析策略[J].中国教育学刊,2004(1).
[2] 王科,汪晓勤.“中美日新”四国高中教材中的数学归纳法比较研究[J].数学教育学报,2015(2).
[3]严家丽,孔凡哲,李清.中美高中数学教材难度特征的比较研究——以《核心数学课》和人教A版教材为例[J].上海教育科研,2014(3).
[4] 曹才翰,章建跃.数学教育心理学[M].北京:北京师范大学出版社,2006.
[5] 张思明,李大永,刘雪莲.高中数学新课程与学生学习[M].北京:高等教育出版社,2008.
[作者:孙成成(1990-),男,安徽淮南人,华中师范大学数学与统计学学院在读硕士研究生;胡典顺(1965-),男,湖北孝感人,华中师范大学教授。]
【责任编辑 郭振玲】

