二阶Emden-Fowler型非线性变时滞微分方程的振荡准则

杨 甲 山

(1.梧州学院 信息与电子工程学院， 广西 梧州 543002; 2.梧州学院 复杂系统仿真与智能计算实验室， 广西 梧州 543002)

二阶Emden-Fowler型非线性变时滞微分方程的振荡准则

杨 甲 山1,2

(1.梧州学院 信息与电子工程学院， 广西 梧州 543002; 2.梧州学院 复杂系统仿真与智能计算实验室， 广西 梧州 543002)

研究了一类具有变时滞的二阶Emden-Fowler型非线性中立型泛函微分方程的振荡性. 借助Riccati变换、积分平均技术和微分不等式等技巧，获得了该类方程振荡的新判别准则和比较判别定理，推广、改进并丰富了现有文献中的结果.

振荡性；变时滞；泛函微分方程；Riccati变换

近来，中立型变时滞泛函方程的振荡性研究引起了国内外学者的广泛兴趣[1-25]. 本文考虑如下形式的二阶非线性中立型变时滞微分方程

[a(t)φ1(z′(t))]′+q(t)f(φ2(x(δ(t))))=0，t≥t0

(1)

的振荡性.式(1)中，z(t)=x(t)+p(t)x(τ(t)),φ1(u)=|u|λ-1u,φ2(u)=|u|β-1u(λ>0,β>0为实常数)；而函数a,p,q∈C([t0,+∞),R)；函数f∈C(R,R)，当u≠0且uf(u)>0时，有

(H1)a∈C1([t0,+∞),(0,+∞))，且q(t)>0，p(t)≥0.

(H3) 存在常数L>0使得当u≠0时，f(u)/u≥L.

若函数x(t)满足a(t)φ1(z′(t))∈C1([Tx,+∞),R)且在区间[Tx,+∞)上满足方程(1)，则称函数x(t)∈C1([Tx,+∞),R)(Tx≥t0)是方程(1)的一个解. 本文只讨论方程(1)的非平凡解. 若方程(1)的解x(t)既不最终为正也不最终为负，则称解x(t)是振荡的，否则是非振荡的；若方程(1)的所有解都是振荡的，则称方程是振荡的.

{a(t)|[x(t)+p(t)x(τ(t))]′|β-1× [x(t)+p(t)x(τ(t))]′}′+q(t)|x(δ(t))|γ-1x(δ(t))=0

(E)

的振动性，得到了方程(E)的若干振动准则，推广、改进并丰富了现有的一些结果. 但文献[14]有限制条件“a′(t)≥0且0≤p(t)<1”，而且当β<λ时没有得到方程(E)的振动准则. 笔者将在条件

(2)

成立的情况下研究方程(1)的振荡性，建立了方程(1)振荡的一个较为精准的判别准则和比较判别定理，改善了对中立项系数函数的限制条件0≤p(t)<1，去掉了条件a′(t)≥0,且β>γ和β<λ2种情形均有方程的振荡准则, 所得准则在β=λ的特殊情形下推广并改进了现有文献中的一系列结果.

引理1[18]设X,Y为非负实数,则

(1)当0<λ≤1时，Xλ+Yλ≥(X+Y)λ,当且仅当X=Y时等号成立.

(2)当λ>1时，Xλ+Yλ≥21-λ(X+Y)λ,当且仅当X=Y时等号成立.

1 主要结果及其证明

为了叙述方便，引入下列3个记号：

Q(t)=min{q(t),q(τ(t))}，

φ+(t)=max{0,φ(t)}，

定理1 设条件(2)成立且0≤p(t)≤p0<+∞(p0为常数)，如果存在函数φ∈C1([t0,+∞),(0,+∞))使得当λ≤β时，有

(3)

当λ>β时，有

(4)

证明 反证法.设方程(1)存在一个非振荡解x(t)，不妨设x(t)为最终正解(当x(t)为最终负解时类似可证)，则∃t1≥t0，使得当t≥t1时，有x(t)>0，x(τ(t))>0，x(δ(t))>0，于是由z(t)的定义知，z(t)>0且(t≥t1).由方程(1)得

[a(t)φ1(z′(t))]′=-q(t)f(φ2(x(δ(t))))≤

-Lq(t)(x(δ(t)))β<0，

(5)

注意到条件(2)，于是由式(5)不难推出z′(t)>0(t≥t1).应用式(5)，当t≥t1时，有

Lq(τ(t))(x(δ(τ(t))))β≤0，

(6)

于是，综合式(5)及(6)，当t≥t1时，可得

[a(t)φ1(z′(t))]′+Lq(t)(x(δ(t)))β+

当0<β≤1时，注意到τ′(t)≥τ0>0，τ°δ=δ°τ及z(t)≤x(t)+p0x(τ(t))以及引理1，则上式可进一步写成

-LQ(t)[x(δ(t))+p0x(δ(τ(t)))]β≤

-LQ(t)zβ(δ(t))≤0.

当β>1时，注意到引理1，类似地，有

-L21-βQ(t)[x(δ(t))+p0x(δ(τ(t)))]β≤

-L21-βQ(t)zβ(δ(t))≤0.

-L0Q(t)zβ(δ(t))≤0.

(7)

考虑到γ和β的取值范围，下面分2种情形进行讨论.

情形1λ≤β.

做Riccati变换：

(8)

则w(t)>0(t≥t1)，注意到τ′(t)≥τ0>0，由式(8)有

(9)

由z(t)>0，z′(t)>0知，存在常数η>0使得当t≥t1时，有z(τ(t))≥η.于是，综合式(9)和(8)，并注意到引理2的不等式，得

(10)

再做Riccati变换：

(11)

则v(t)>0(t≥t1)，类似于上面的推导过程，可得

(12)

综合式(10)和(12)，并注意到式(7)及z′(t)>0，有

(13)

由式(5)知，a(t)[z′(t)]λ(t≥t1)是单调减小的，因此有

即

(14)

将式(14)代入式(13)，得

于是有

与式(3)矛盾.

情形2λ>β.

(15)

再做如式(11)所示的Riccati变换，与式(12)的推导过程类似，可得

(16)

综合式(15)、(16)，z′(t)>0及式(7)和(14)，可得

-L0φ(t)Q(t)Ψβ(t,t1)+

因此，

与式(4)矛盾. 定理证毕.

定理2 设条件(2)成立，并且0≤p(t)≤p0<+∞(p0为常数)，如果一阶微分不等式

yβ/λ(δ(t))≤0

(17)

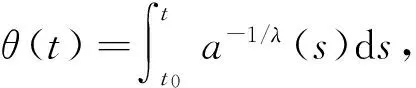
证明 反证法：设方程(1)存在一个非振荡解x(t)，不妨设x(t)为最终正解(当x(t)为最终负解时类似可证)，则∃t1≥t0，使得当t≥t1时，有x(t)>0，x(τ(t))>0，x(δ(t))>0. 由定理1的证明知，式(7)成立，于是由式(7)得

(18)

由于当t≥t1时,z′(t)>0，[a(t)φ1(z′(t))]′=[a(t)(z′(t))λ]′<0，所以当t≥s≥t1时，有a(t)(z′(t))λ≤a(s)(z′(s))λ，即a1/λ(s)z′(s)≥a1/λ(t)z′(t)，因此

a1/λ(t)z′(t)[θ(t)-θ(t1)]，

由式(18)并记y(t)=a(t)(z′(t))λ，于是可得

L0Q(t)aβ/λ(δ(t))(z′(δ(t)))β[θ(δ(t))-θ(t1)]β=

θ(t1)]βyβ/λ(δ(t))，

表明y(t)是式(17)的一个正解，矛盾. 定理证毕.

注1 显然, 本文给出了一类非常广泛的二阶Emden-Fowler泛函微分方程(1)振荡的2个判别准则，改善了现有研究(如文献[14])对中立项系数函数的限制条件：0≤p(t)<1. 从定理1可看出，λ>β和λ<β方程的振荡条件是有差别的. 此外，从以下例子还可以看出，本文结果的特殊情形即定理1中当λ=β且p0=1时，其振荡结果也是较“精细的”，这些结果推广、改进并丰富了现有文献的结论.

2 实例分析

例1 对常数q0>0，考虑二阶时滞微分方程

(E1)

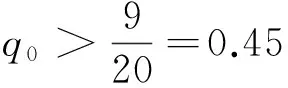
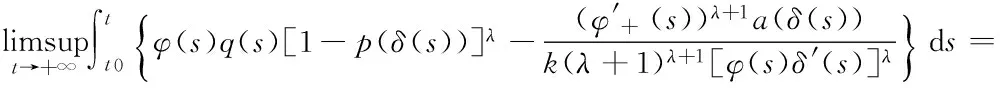
由文献[11]定理2.1知，当q0>1.25时方程(E1)是振荡的. 因此，本文定理1不仅包括了文献[11]中的定理2.1，而且改进了文中的相关定理.

例2 考虑二阶泛函微分方程

(E2)

取f(u)=u[1+ln(1+u4)]，由于

显然条件(H1)～(H3)全部满足. 又因为

取φ(t)=1，则

定理1的条件均满足，故由定理1知，方程(E2)是振荡的.

注3 由于方程(E2)的中立项系数函数p(t)>1,λ≠β且不满足a′(t)≥0，因此文献[1-8,11-19]中的定理均不能用于方程(E2). 值得注意的是,本文定理条件(H2)中要求τ°δ=δ°τ, 因此当τ°δ≠δ°τ时,寻找新的技术手段来研究方程(1)的振荡性, 这将是非常有意义的事情.

[1]HASANBULLIM,ROGOVCHENKOYV.Oscillationcriteriaforsecondordernonlinearneutraldifferentialequations[J]. Applied Mathematics and Computation,2010,215(12):4392-4399.

[2] LI T X, AGARWAL R P, BOHNER M. Some oscillation results for second-order neutral differential equations[J]. The Journal of the Indian Mathematical Society,2012,79(1/2/3/4):97-106.

[3] LI T X, AGARWAL R P, BOHNER M. Some oscillation results for second-order neutral dynamic equations[J]. Hacettepe Journal of Mathematics and Statistics,2012,41(5):715-721.

[4] LI T X, ROGOVCHENKO Y V. Oscillatory behavior of second-order nonlinear neutral differential equations[J]. Abstract and Applied Analysis,2014:ID143614.

[5] SUN S R, LI T X, HAN Z L,et al. Oscillation theorems for second-order quasilinear neutral functional differential equations[J]. Abstract and Applied Analysis,2012:ID819342.

[6] ZHANG C H, AGARWAL R P, BOHNER M, et al. New oscillation results for second-order neutral delay dynamic equations[J]. Advances in Difference Equations,2012:227.

[7] ZHONG J,OUYANG Z, ZOU S. An oscillation theorem for a class of second-order forced neutral delay differential equations with mixed nonlinearities[J]. Applied Mathematics Letters,2011,24(8):1449-1454.

[8] AGARWAL R P, BOHNER M, LI T X, et al. A new approach in the study of oscillatory behavior of even-order neutral delay differential equations[J]. Appl Math Comput,2013,225:787-794.

[9] YANG J S, QIN X W. Oscillation criteria for certain second-order Emden-Fowler delay functional dynamic equations with damping on time scales[J]. Advances in Difference Equations,2015:97.Doi:10.1186/S13662-014-0328-X.

[10] YANG J S, QIN X W, ZHANG X J.Oscillation criteria for certain second-order nonlinear neutral delay dynamic equations with damping on time scales [J]. Mathematica Applicata,2015,28(2):439-448.

[11] YE L, XU Z. Oscillation criteria for second order quasilinear neutral delay differential equations[J]. Applied Mathematics and Computation,2009,207(2):388-396.

[12] LI T X, ROGOVCHENKO Y V, ZHANG C H. Oscillation of second-order neutral differential equations[J]. Funkcialaj Ekvacioj,2013,56(1):111-120.

[13] AGARWAL R P, BOHNER M, LI T X, et al. Oscillation of second-order Emden-Fowler neutral delay differential equations[J]. Annali di Matematica Pura ed Applicata,2014,193(6):1861-1875.

[14] 黄记洲,符策红.广义Emden-Fowler方程的振动性[J].应用数学学报,2015,38(6):1126-1135. HUANG J Z, FU C H. Oscillation criteria of generalized Emden-Fowler equations[J]. Acta Mathematicae Applicatae Sinica,2015,38(6):1126-1135.

[15] 杨甲山,方彬.一类二阶中立型微分方程的振动性[J].数学的实践与认识,2013,43(23):193-197. YANG J S, FANG B. Oscillation of a class of second order neutral differential equations[J]. Mathematics in Practice and Theory,2013,43(23):193-197.

[16] 杨甲山.具阻尼项的高阶中立型泛函微分方程的振荡性[J].中山大学学报:自然科学版,2014,53(3):67-72. YANG J S. Oscillation of higher order neutral functional differential equations with damping[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2014,53(3):67-72.

[17] 杨甲山.具正负系数和阻尼项的高阶泛函微分方程的振动性[J].华东师范大学学报:自然科学版,2014(6):25-34. YANG J S. Oscillation of higher order functional differential equations with positive and negative coefficients and damping term[J]. Journal of East China Normal University: Natural Science,2014(6):25-34.

[18] XING G J, LI T X, ZHANG C H. Oscillation of higher-order quasi-linear neutral differential equations[J]. Advances in Difference Equations,2011:45.Doi:10.1186/1687-1847-2011-45.

[19] 杨甲山,覃学文.具阻尼项的高阶Emden-Fowler型泛函微分方程的振荡性[J].中山大学学报:自然科学版,2015,54(4):63-68. YANG J S, QIN X W. Oscillation of higher hrder Emden-Fowler functional differential equations with damping[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2015,54(4):63-68.

[20] 杨甲山,黄劲.时间模上一类二阶非线性动态方程振荡性的新准则[J].华东师范大学学报:自然科学版,2015(3):9-15. YANG J S, HUANG J. New criteria for oscillation of certain second-order nonlinear dynamic equations on time scales[J]. Journal of East China Normal University :Natural Science,2015(3):9-15.

[21] 杨甲山,孙文兵.具正负系数的二阶差分方程的振动性[J].山东大学学报:理学版,2011,46(8):59-63. YANG J S, SUN W B. Oscillation of second order difference equations with positive and negative coefficients[J]. Journal of Shandong University:Natural Science,2011,46(8):59-63.

[22] 赵雪芹.非线性微分方程精确解及振动性[D].大连:大连理工大学,2007. ZHAO X Q. Exact Solutions and Oscillation of Nonlinear Differential Equations[D]. Dalian: Dalian University of Technology,2007.

[23] 莫协强,张晓建,杨甲山.一类高阶泛函微分方程非振动解的存在性[J].四川师范大学学报:自然科学版,2014,37(6):861-866. MO X Q, ZHANG X J, YANG J S. Existence of nonoscillatory solutions for a class of higher order functional differential equations[J]. Journal of Sichuan Normal University:Natural Science,2014,37(6):861-866.

[24] YANG J S. Oscillation of third-order delay dynamic equations on time scales[J]. Chinese Quarterly Journal of Mathematics,2014,29(3):447-456.

[25] 杨甲山.具可变时滞的二阶非线性中立型泛函微分方程的振动性[J].浙江大学学报:理学版,2016,43(3):257-263. YANG J S. Oscillation of certain second-order nonlinear neutral functional differential equations with variable delay[J]. Journal of Zhejiang University:Science Edition,2016,43(3):257-263.

YANG Jiashan1，2

(1.SchoolofInformationandElectronicEngineering,WuzhouUniversity,Wuzhou543002,GuangxiZhuangAutonomousRegion,China; 2.LaboratoryofComplexSystemsSimulationandIntelligentComputing,WuzhouUniversity,Wuzhou543002,GuangxiZhuangAutonomousRegion,China)

The purpose of this article is to study the oscillatory behavior of second-order Emden-Fowler nonlinear neutral functional differential equations with variable delay. By using the Riccati transformation, integral averaging technique and differential inequalities, we established a new oscillation criteria and a comparison theorem for the oscillation of the equations. These criteria dealing with some cases have not been covered by the existing results in the literature.

oscillation; variable delay; functional differential equation; Riccati transformation

2016-03-26.

梧州学院2014年校级科研重大项目(2014A003); 硕士学位授予单位立项建设项目(桂学位[2013]4号);广西教育厅科研项目(2013YB223).

杨甲山(1963-), ORCID:http://orcid.org/0000-0002-0340-097X, 男, 学士， 教授, 主要从事微分方程的理论与应用研究，E-mail:syxyyjs@163.com.

10.3785/j.issn.1008-9497.2017.02.004

O 175. 7

A

1008-9497(2017)02-144-07

Oscillation criteria of second-order Emden-Fowler nonlinear variable delay differential equations. Journal of Zhejiang University(Science Edition), 2017,44(2):144-149,160