小学数学前概念资源利用的教学策略
林智
小学数学教学中,在学习某个概念之前,学生已对周围与之相关的事物及现象有了一定的认识和了解,同时初步形成了一些自己的观点和看法,这些看法我们称之为前概念。学生的前概念有些是错误的,有些是模糊的,但也有一些是正确的。基于对小学数学前概念教学的调查与分析,可把学生的前概念分为三类:与科学概念截然不同的,与科学概念部分相似的,与科学概念完全一致的。前概念教学就是进行合理的概念转变,是对学生前概念的纠正、澄清和同化,是一个复杂的认知建构过程。
在实际教学中,学生带着各种前概念进入数学课堂,如果利用不好可能会影响数学新概念的建立,阻碍数学新概念的形成,成为概念教学的绊脚石。倘若教师察知到位并合理利用前概念,那么前概念就是教学的有利资源,就能帮助学生快速、准确地构建科学概念。
一、基于错误前概念,探寻纠正策略
1.创设认知冲突,纠正错误前概念
认知冲突是一种认知矛盾,是学生原有认知结构和新知识之间不一致时所形成的状态,教师需要提前了解、分析学生的前概念,并在课堂教学中合理创设冲突点激发学生的参与意识,在参与活动中纠正学生错误的前概念,使学生重新认识并改变自己的观点,达到新的认知平衡。
如教学人教版《数学》四年级下册“三角形的特性”中的稳定性时,为了纠正学生错误的前概念——长方形也具有稳定性(因为平常见到的门窗是长方形且是固定的),创设如下的情境:先让学生拉一拉三角形和长方形的框架,得出长方形容易变形而三角形不易变形。接着出示用塑料吸管围成的三角形,让学生试着拉一拉,有学生发现有一些变形。此时便产生了认知上的冲突,教室里出现了一些躁动。然后再让学生用3根小棒摆出一个三角形,用4根小棒摆出一个四边形。学生通过观察惊奇地发现,用3根小棒摆出的图形只有一种形状(三角形),而4根小棒则摆出了很多种形状不同、大小不一的四边形。在强烈的视觉冲击下,学生很自然地体会到三角形具有稳定性(唯一性)而四边形不具备,真正領悟三角形稳定性的本质含义。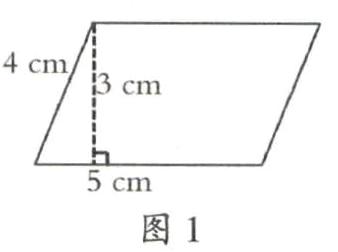
教学中,为了纠正与科学概念矛盾的错误前概念,需要经历“暴露错误前概念—探寻科学概念—纠正错误前概念—形成科学概念”的探究过程,使学生在概念修正与完善的过程中,培养探究的能力,体验探究的乐趣,让学生在体验中建立科学的新概念。
2.开展探究活动,弱化错误前概念
探究式教学基于每位学生自主学习、探究问题的天性,将学生置于一种主动探究、解决实际问题的学习状态中,让学生通过自己的亲身体验来经历知识的形成和发展过程,引发强烈的认知冲突,转变前概念,建立正确的科学概念。
如教学人教版《数学》三年级下册“面积单位”时,开展如下探究活动:先让学生比较两个差异明显的图形,通过观察得出一致的结论,接着出示大小差异不明显的两个图形,使学生认识到直觉观察无法判断,从而想到用重叠的方法去比较,紧接着出示用重叠法也不能直接比出两个图形的大小,学生再次陷入迷惘,想出新办法,用摆小正方形或数方格的方法去比较。至此,给出两个方格数一样多但方格大小不一的两个图形分别给两组学生看,通过方格数的比较达到一致(面积“一样大”),再把刚才两个图形出示给全班同学进行比较,顿时惊住了。从这样一步一步的深入探究中,学生真正体会到方格的大小必须一样(即比较的标准要统一),才能比较大小,然后顺势推出面积单位。
这样的设计,不仅让学生体验到面积大小比较方法的多样性,而且让学生感受到统一面积单位去比较大小的必要性,同时又弱化了学生对面积认识的错误前概念。
3.紧扣课堂生成,消除错误前概念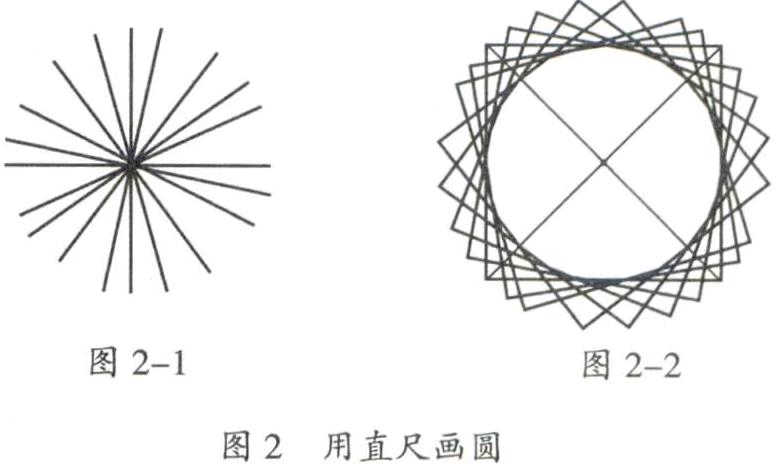
概念的形成和发展过程对于每位学生来说都是不一样的,因为他们会依据自己独特的思维方式和生活经验进行学习。“生成”是以学生原有的知识结构作为新知识的“生长点”,依据具体情境及其变化对教学行为和过程不断地做出调整和创造教学。
如教学人教版《数学》五年级上册“平行四边形的面积”时,出示图1,老师问:你知道这个平行四边形的面积是多少?生1:
5×3=15(cm2)。生2:5×4=20(cm2)。追问:那平行四边形的面积到底是多少?它与什么有关系?有着怎样的关系?请同学们根据提供的学具进行探究。每位学生结合自己的原有认知,开展方式不同的探究。有的学生沿着平行四边形的高剪下,通过剪、移、拼的方法转化成长方形,长方形的长相当于平行四边形的底,宽相当于平行四边形的高,根据“长方形的面积=长×宽”,得到“平行四边形的面积=底×高”;有的学生没有沿高剪下,也可以得到一个平行四边形,但无法求出平行四边形的面积,从而产生了疑问。经过同学之间的合作探究、汇报交流、再次操作,大家渐渐地领悟、慢慢地体会到平行四边形的面积与它的底和高有关,从而消除了平行四边形的面积与邻边有关的错误前概念,建立正确的平行四边形面积计算方法。
二、基于含糊前概念,调整澄清策略
1.铺垫概念形成时,感受概念生长处
概念的形成、转变不是一朝一夕、一蹴而就的事情。教学中,教师不要急于求成,要包容学生模糊的前概念,耐心等待学生认知的生长,保持良好的教学心态。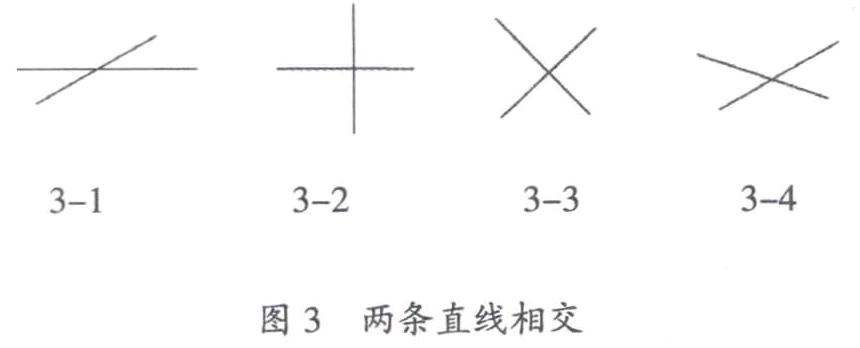
如教学人教版《数学》六年级上册“圆的认识”时,基于前测,得知学生对圆都有一定的认识,能简单描述圆的特征,但对圆的本质属性(到定点距离等于定长)就知之甚少了。同时,学生容易掌握圆的一些基本特征,但为什么用圆规画圆跟定点和定长有关,这个概念是模糊的。为此可以创设如下教学情境,为圆概念的形成埋下伏笔。在用圆规画圆后,交给学生一个任务:用直尺画圆。教师引导学生采用以下两种方法。
图2-1方法:在纸上定一个点,再从这个点出发画长2cm长的线段,画得越多越好,接着把每条线段的另一个端点用曲线连起来。
图2-2方法:用直尺取一段长4 cm的线段作为圆的直径,找到这条线段的中心,把这个中心作为圆的圆心,然后用这条线段的长度作一个正方形,就这样作无数个正方形,这些正方形围成的图形就是一个圆。
通过实践操作活动,使学生真正明白为什么圆要有定点和定长。
从多种方法中,引导学生探索定点与定长之间的距离关系,从而渐渐明晰圆上的所有点到一个定点的距离都相等,为感受圆的本质属性埋下伏笔,在这样的教学铺垫中,学生的科学概念得到生长。
2.架设概念新桥梁,形成概念新表象
表象是指人们经过感知的客观事物在头脑中再现的形象。其形象常常会在头脑中以痕迹的形式保留下来,以后这种事物虽不出现,但在一定条件的刺激下,它的形象仍会在头脑中再现。心理学研究表明,感知材料越丰富,活动体验越充分,建立的表象就越清晰,概念就越清晰。
如教学人教版《数学》二年级上册“长度单位”时,很多教师都非常重视1 cm长度概念的建立,让学生在生活中找1 cm,比划一下,哪些物体的长度约为1 cm,学生会欣喜地发现,指甲盖长度、田字格的边长、图钉高度约为1 cm,学生在估计、测量、再估计、再测量中建立1 cm概念的同时,建构2 cm、3 cm甚至更多的空间表象,为以后更多的空间观念架设起桥梁。
通过这样的教学,使学生把抽象的单位概念转化成本来就熟悉的、具体的物体,通过触摸事物,找到物体的长度,测一测、估一估长度,从而逐步建构单位的空间观念,形成正确的单位表象,真正形成正确的空间观念。
3.依循学生思维,建立科学概念
通过对学生前概念的调查与分析,可以让我们全面真实地了解学生的知识起点与思维起点。因此在教学预设时,要紧扣学生的前概念组织材料、设计问题,再根据学生的知识起点与思维起点组织教学。
如在教学人教版《数学》四年级上册“垂直和平行”時,让学生在白纸上任意画出两条直线,结合学生作品进行分类得到相交的作品(如图3),请学生仔细观察哪种情况最特殊,结果87.6%的学生认为只有3-2是垂直的,他们心目中的垂直就是 “竖着的一条直线”,面对这一概念的描述,我们不能将3-3也是垂直强加给学生,而是先让大家比较两条直线的关系,发现他们的位置有“直的”也有“斜的”,说3-2是“直的”,3-3是“斜了”。再让学生通过反复的观察、比较,发现“直的”真正含义就是两条直线相交后的角是直角,“斜的”本质就是相交后的角不是直角。根据这样的辨析,把垂直的两幅图圈到一起,并表述:像这样相交成直角的两条直线,叫做互相垂直。
依循学生的思维,暴露学生的想法,再顺水推舟,顺着学生的思维设计问题,通过分析、比较,在问题解决中逐步领悟,最终形成正确的科学概念。
三、基于正确前概念,组织同化策略
1.在比较中渗透
小学数学教材中有许多既有联系又有区别的教学内容,倘若在教学中充分运用比较的方法,则有助于突出教学重点、突破教学难点,使学生容易接受新概念,防止概念混淆,提高辨别能力和思维能力。
如教学人教版《数学》二年级下册“锐角和钝角”时,从前测中了解到,学生能准确地判断这些角,只不过专业术语描述不够完整、全面罢了。为此,我们在教学中首先复习直角,然后用直角引出锐角、钝角,同时借助教具演示,用直角器和锐角、钝角进行比较,比直角小的角是锐角,比直角大的角是钝角,这样锐角和钝角的概念就在学生眼前渐渐地明朗起来。
运用比较的方法建立概念,既有助于理解数学概念,又利于建构数学概念,还有助于发展学生的逻辑思维能力。
2.在应用中深化
学生在学习一个新概念后,为了巩固所学,在教学中应设计所学概念与易混淆概念的比较练习,帮助学生全面、正确理解概念,在运用中理解、掌握科学概念,暴露概念理解中的缺陷,以便有针对性地对所学概念加以纠正、完善和深化。
对于易混淆概念的同学,他们的概念形成需要时间消化,也需要在不断的练习应用中深化。因此在教学中,教师要关注学生在科学概念建立过程中的负迁移及容易出现的问题,了解学生的认知结构和能力状况,有针对性地选择一些典型的习题,帮助学生更好、更全面、更深入地理解和掌握科学概念。
3.在系统中整合
概念的理解与建立需要一个过程,也需要时间去消化,更需要学生在一个系统整合的过程中巩固。当学生在前概念的基础上形成了正确的数学概念后,还需要通过实际问题的解决加以巩固,把新知识与学生的前概念进行整合,使新知识得到有效地巩固,建构起有张力的知识网络。
如教学人教版《数学》三年级下册“面积与面积单位”时,当学生建立了面积单位的概念后,让学生估一估身边熟悉物体的面积,再用面积单位测一测。随后安排适当的巩固练习,将新知识融入已有知识体系。
总之,在数学教学中,学生在学习之前已对知识有了一定的认识,这些认识或错误、或模糊、或正确,教师在教学之前需要提前了解,准确把握学生学习的知识起点和思维起点。教学预设时立足学生的前概念,运用各种有效的教学策略,把前概念作为产生和孕育科学概念的“生长点”,促使学生的前概念能顺利转变为科学概念,从而建立完整、正确的科学概念。这样,才能提高教学的有效性,才能让学生真正理解和掌握数学的基本知识与技能,进而获得数学的基本思想和积累基本的活动经验。
参考文献
[1] 李高峰,刘恩山.前科学概念的研究进展[J].内蒙古师范大学学报,2007(4).
[2] 雷永生,王至元,杜丽燕.皮亚杰发生认知论评述[M].北京:人民出版社,1987.
[3] 吴继敏.科学课上改变学生错误前概念的概念教学[A].江苏省教育学会2006年年会论文集(理科专辑)[C],2006.
[4] 蔡铁权,姜旭英,胡玫.概念转变的科学教学[M].北京:教育科学出版社,2009.
[5] 王岳.小学科学教育中儿童概念学习问题探讨[M]北京:人民教育出版社,2000.
[6] 窦轶洋,高凌飚,等.论学生前概念及教学的启示[J].学科教育,2007(10).
[责任编辑:陈国庆]

