采用动态灰聚类算法的风电场动态等值方法

方瑞明， 吴敏玲， 王彦东， 尚荣艳， 彭长青

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

采用动态灰聚类算法的风电场动态等值方法

方瑞明， 吴敏玲， 王彦东， 尚荣艳， 彭长青

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

由于风力发电的间歇性与随机波动性特征，大规模风电并网对电力系统的稳定性影响愈发显著[1-2].为了提高风电并网电力系统的分析精度，优化风电并网的控制策略，文献[3-12]借鉴传统电力系统动态等值中的同调等值法并结合某些聚类算法，将实测运行数据应用于风电场的动态多机等值建模方法中.然而，上述文献在应用实测运行数据进行风电场动态等值建模过程中，大多仅考虑了不同风速或风电功率数据对模型的影响.风电机组的发电过程是一个将风能转化为旋转机械能，再由旋转机械能转化为电能并向电网输出的复杂过程[13].其输出特性不仅受到风速等外部因素影响，还与机组内各部件和子系统的相互作用和耦合密切相关.因此，有必要从时间维度和空间维度综合分析考虑风电机组实测运行数据对风电场等值模型精度的影响.然而，风电机组的实测运行数据具有繁杂冗余的特点，如果不能对风电机组的外部特性与运行数据之间的关联性进行全面挖掘，则所建模型计算复杂度过高，缺乏实用价值.灰色关联分析理论是一种能够通过较少数据量来处理不确定关联性因素的有效方法[14]，它能够将不确定性量化，使系统“白化”，从而表现风电机组运行状况间的动态灰色关联性.本文结合灰色关联分析理论，提出一种基于动态灰聚类算法的风电场动态等值建模方法.

1 基于实测运行数据的风电机组间关联性分析

自相关特性分析实质上是，将一个时间序列经由时间Δt平移得到另一个序列，通过计算两个序列间的自相关系数来描述当前数据值与时刻前数据变化的一致性.自相关系数ρΔt的计算式为

(1)

式(1)中:cov(·)为协方差；var(·)为方差.ρΔt绝对值越大，则序列随时间变化的相关性越强.

首先,对风电场实测运行数据进行自相关特性分析，数据可从机组的数据采集与监控(SCADA)系统获得.以某风电场为例，该风电场组的SCADA系统涉及的连续量监测项目共20项，计算各机组监测项目数据序列的自相关系数,并进行分析及对比.由于篇幅关系，文中仅选取风速、有功功率、发电机转速和齿轮箱输入轴温度为代表(其余16项监测项目的分析结果是一致的)，结果如图1所示.

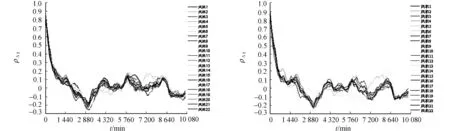
(a) 风速 (b) 有功功率

(c) 发电机转速 (d) 齿轮箱输入轴温度图1 各风电机组7 d数据序列的自相关系数Fig.1 Autocorrelation coefficients of main index of wind turbines during seven days

图2 各风力发电机组1 d数据序列的风速自相关系数Fig. 2 Wind speed autocorrelation coefficient of main index during one day

由图1可知：各风力发电机组相同项目数据序列对应的自相关系数，随时间跨度变化呈快速地无规律衰减振荡趋势；同一机组不同项目数据序列对应的自相关系数曲线较为相似，不同机组相同项目数据序列对应的自相关系数分布较为接近.这表明机组运行是个动态变化很快的过程，影响机组运行状况的因素间有着紧密的耦合相关，各机组运行状况间存在着不确定关联性，即灰色关联性.

由于风电机组运行是个快速动态变化过程，因此，应用风电场实测运行数据进行风电场动态等值建模时，只需取自相关性较强数据，一般认为自相关系数降到0.3以下的数据与当前时刻的数据相关性较弱[15].1 d内22台风力发电机组风速数据序列的自相关系数曲线，如图2所示.其他相关项目的曲线与此类似，限于篇幅不再给出.由图2可知：对风电场实测运行数据进行分析时，以7 h(420 min)为跨度截取样本较为适宜.

2 基于动态灰聚类算法的风电场动态等值模型

2.1 基于动态灰聚类算法的机群划分

结合动态灰关联分析，构造出一个能体现风电机组运行状况间动态灰色关联性的关联度矩阵.然后，将其作为机群划分的聚类指标进行K均值聚类.从而改善传统聚类指标数据繁杂或包含信息不全的缺点，得出更合理的机群聚类结果，具体有以下10个主要步骤.

1) 风电场实测运行数据的收集及预处理.

2) 设某风电场为一个评价大系统，即{Xi，j∈(Si，Xj，Tt)}m·n·N，i=1，2，…，m；j=1，2，…，n；t=1，2，…，N.其中:Si为某时刻t第i台风电机组的运行状况；Xj为式(1)中选取的第j项监测项目；Tt为数据预处理后选定的第t个时刻；m为机组台数；n为监测项目个数；N为时刻个数.

3) 定义A1，A2，…，An为不同时刻各风力发电机组运行状况监测项目的信息矩阵，即

其中：xi，j(t)为第t个时刻第i台风机的第j项监测项目经数据预处理后的运行数据.

4) 计算各时刻的各监测项目实测运行数据时间维度上的最大均值，有

(2)

5) 对数据预处理后得到的小数据样本进行归一化(无纲量化)处理，即有

(3)

6) 令表示某时刻单台风力发电机组运行状况的比较序列为

7) 令表示所有风电机组综合运行状况的动态参考序列为

8) 计算各时刻、各机组运行状况的比较序列Si(t)与参考系统S0(T)之间的灰色关联度，即有

(4)

9) 所求的灰色关联度矩阵G,其计算式为

(5)

式(5)中:γt，i为在时刻t第i台机组运行状况与所有机组综合运行状况间的灰关联度；gi为数据样本所选时间跨度内第i台机组运行状况的灰关联度变化序列.

10) 选取G中样本组作为聚类指标，计算样本组间的欧氏距离di，j进行K均值聚类，结果为

(6)

通过计算样本组i的轮廓值S(i)判断聚类结果的合理性，即有

(7)

式(7)中:a为样本i与同簇其他样本之间的平均距离；b为一个向量，其元素是样本i与不同簇的簇内样本之间的平均距离.S(i)取值范围为[-1，1]，S(i)值越大于0，说明样本i的分类越合理;否则，S(i)小于0,则说明样本i的分类不合理，还有比目前分类更合理的方案[6].

2.2 等值模型参数计算

假定同一类机群内有M台风力发电机组，则同群机组等值参数[16]为

(8)

式(8)中:下标eq代表等值参数；M为等值机组数；H，K，D分别表示惯性时间常数、轴系刚度系数、轴系阻尼系数.

由于风电场的集电系统对风电场实际出力有较大影响[17]，因此，还需对风电场集电系统进行等值.集电系统等值采用等值损耗功率法[18]，主要等值参数线路阻抗Zeq的计算式为

(9)

式(9)中:Zk为第k条电缆阻抗；Pj为第j台风力发电机组的输出功率.

3 实例仿真分析

3.1 某实际风电场的动态等值

基于某实际风电场进行分析，该风电场内共有22台风力发电机组，单机额定容量为1.5MW.该风电场公共连接点(PCC)为35kV母线，经由T1升压至110kV.为便于比较，将此风电场接入IEEE39节点系统的35节点处，风电场详细模型单线示意图，如图3所示.在中国电力科学研究院所研发的电力系统全数字仿真平台上,搭建该系统模型,并进行仿真分析.

图3 某实际风电场详细模型示意图Fig.3 Detailed model of an actual wind farm

根据前文分析，具体有如下3个主要的动态等值步骤.

1) 风电场实测运行数据的收集及预处理.选取该风电场2012年10月14日8：02～15:02间7 h的20项SCADA系统连续量监测数据进行分析.剔除故障数据后，以每30 min为间隔随机选取一个样本，最终从这7 h各台风力发电机组20项监测项目数据内确定13个时刻的小数据样本.

2) 机群划分.基于选取的小数据样本，计算机组运行状况间灰色关联度矩阵G,如图4所示.由图4可知:从空间横向比较，风电机组运行状况间的灰色关联度γ(i,t)是不同的，表现了风电机组运行状况间的灰色关联性；从时序纵向比较，各台风力发电机组运行状况的灰色关联度是动态变化的，表现了各台风力发电机组运行状况受多方面因素影响的随机动态波动性.因此,所求灰色关联度矩阵作为聚类指标，能够从时间与空间的角度量化地反映出风电机组运行状况间的动态灰色关联性，且其数据量少，满足建模的需求.

图4 风电机组运行状况间灰色关联度矩阵三维图Fig.4 3D graph of gray relational grade matrix about operation condition of wind turbines

基于同段时间风速数据和矩阵G的机群聚类结果，如表1所示.对应样本轮廓值S(i)，如图5所示.由图5可知：对聚类后样本S(i)进行计算，均大于0，表明聚类结果是达标的.

表1 不同聚类结果的机群聚类划分结果

由表1可知:依据风速数据得出的机群聚类结果比较分散，聚类结果仅片面地表现出风电机组间风速的差异性;依据灰色关联度矩阵得出的机群聚类结果大致符合按地理位置划分的规律，但机组WT6,WT8,WT19与WT20却没有划分到与之地理位置较近的机群里.这是由于受到天气、上游风电机组尾流效应、电网运行状况等灰色因素的影响.说明通过灰色关联矩阵作为聚类指标进行K均值聚类，能够将风电机组运行状况间隐藏的动态灰色关联信息全面地反映出来，得到更合理的机群聚类结果.

3) 根据式(8)，(9)计算同群机组等值参数，得到等值后的风电场模型.

3.2 仿真分析

分别对电网侧三相接地短路故障和阵风扰动两种情况进行仿真分析.其中：在电网侧三相接地短路故障情况下，设系统在t=1.00 s时，母线24发生三相接地短路故障，在t=1.12 s时故障消除；而在阵风扰动情况下，设迎向风电场的阵风4 s启动，8 s结束，阵风最大值为3 m·s-1.分别采用传统单机等值模型、基于风速实测运行数据等值模型、基于动态灰聚类算法的等值模型和基于风电机组物理模型所搭建的详细模型(简称详细模型)进行分析，得到风电场PCC母线的无功功率(Q)、有功功率(P)的动态响应曲线，如图6,7所示.

(a) 有功功率 (b) 无功功率图6 短路故障时风电场的动态响应曲线Fig.6 Dynamic response curves of wind farm with short circuit fault

(a) 有功功率 (b) 无功功率图7 风速扰动时风电场的动态响应曲线Fig.7 Dynamic response curves of wind farm with gust disturbance

由图6,7可知:文中所提出的基于动态灰聚类算法的风电场动态等值建模方法，其结果与详细模型最为接近.这说明对实测运行数据进行自相关分析并引入动态灰聚类算法进行信息挖掘，可使机群划分结果更能反映风电机组运行状况间的动态灰色关联性.它不仅改善传统做法聚类时其指标信息不全的缺点，还可以有效地减少实测运行数据的繁杂冗余度，在提高模型精确度的同时，降低所建模型的计算复杂度.

4 结束语

提出动态灰聚类算法的风电场动态等值建模方法，使风电机组运行状况间的动态灰色关联性全面包含在聚类指标中，提高了风电场多机动态聚类等值效果，同时还克服了详细模型建模过程复杂、仿真时间长和单机模型精度低的不足.通过实例仿真分析可以看出：所建立的动态灰聚类算法的风电场动态等值模型的动态响应特性与详细模型较接近，能够较准确地反映风电场并网点的动态特性，适用于对风电并网暴露出的故障问题进行暂态稳定分析，具有重要的工程应用价值.

[1] 李洪美，万秋兰，向昌明.考虑风速的风电场等值方法[J].电力自动化设备，2013，33(1):121-123，159.

[2] ZOU Jianxiao，PENG Chao，XU Hongbing，etal.A Fuzzy clustering algorithm-based dynamic equivalent modeling method for wind farm with DFIG[J].IEEE Transactions on Energy Conversion，2015，30(4)：1329-1337.

[3] 葛江北，周明，李庚银.大型风电场建模综述[J].电力系统保护与控制，2013，41(17):146-153.

[4] CHOWDHURY M A，HOSSEINZADEH N，BILLAH M M.Dynamic DFIG wind farm model with an aggregation technique[C]∥Electrical and Computer Engineering.Dhaka:IEEE Press，2010:330-333.

[5] 刘力卿，李秀锦，余洋，等.变速恒频双馈风电机组风电场动态出力特性建模方法[J].电力科学与工程，2011，27(12):7-11.

[6] 陈树勇，王聪，申洪，等.基于聚类算法的风电场动态等值[J].中国电机工程学报，2012，32(4):11-19.

[7] ALI M，ILIE I S，MILANOVIC J V.Wind farm model aggregation using probabilistic clustering[J].IEEE Transactions on Power Systems，2013，28(1):309-316.

[8] 范国英，史坤鹏，郑太一，等.风电场集群接入系统后的聚类分析[J].电网技术，2011，35(11):62-66.

[9] 林俐，陈迎.基于扩散映射理论的谱聚类算法的风电场机群划分[J].电力自动化设备，2013，339(6):113-118.

[10] ZHAO Zhouli，YANG Ping.Dynamic equivalent modeling of wind farm with double fed induction wind generator based on operating data[C]∥Power Electronics Systems and Applications.Hong Kong:IEEE Press，2013:1-6.

[11] 苏勋文，米增强.基于运行数据的风电机组建模方法[J].电力系统保护与控制，2010，38(9):50-55.

[12] 林俐，潘险险.基于分裂层次半监督谱聚类算法的风电场机群划分方法[J].电力自动化设备，2015，35(2):8-14.

[13] 梁颖，方瑞明.基于SCADA和支持向量回归的风电机组状态在线评估方法[J].电力系统自动化，2013，37(14):7-31.

[14] 杨良军，熊小伏，张媛.基于灰色关联度和理想解法的电力设备状态维修策略[J].电力系统保护与控制，2009，37(18):74-78.

[15] 史书良.统计学原理[M].北京:清华大学出版社,2009:227-234.

[16] 米增强，苏勋文，杨奇逊，等.风电场动态等值模型的多机表征方法[J].电工技术学报，2010，25(5):162-169.

[17] 王碧阳，王锡凡，王秀丽，等.考虑集电系统的风电场可靠性评估[J].中国电机工程学报，2015，35(9):2105-2111.

[18] MULJADI E，BUTTERFIELD C P，ELLIS A，etal.Equivalencing the collector system of a large wind power plant[C]∥IEEE Power Engineering Society General Meeting.Montreal:IEEE Press，2006:1-6.

(责任编辑： 钱筠 英文审校： 吴逢铁)

Dynamic Equivalence of Wind Farm Based on Dynamic Gray Cluster Algorithm

FANG Ruiming， WU Minling， WANG Yandong，SHANG Rongyan， PENG Changqing

(College of Information Science and Engineering， Huaqiao University， Xiamen 361021， China)

The characteristics of dynamic gray correlation among the different operation conditions of wind turbines are considered, and then a method of dynamic equivalence for wind farm based on dynamic gray clustering algorithm is proposed. Firstly, the correlation relationship among the wind turbines is analyzed by using the measured data, and the time span of data sample is determined. Secondly, a correlation matrix, named G, is constructed based on dynamic gray correlation analysis method, which can describe the characteristics of dynamic gray correlation among the different conditions of wind turbines. Thirdly, theK-means cluster method is adopted to divide all wind turbines in the wind farm into several groups. Meanwhile, the sample groups in G are used as clustering index. Finally, the equivalent parameters of each group are calculated by using the capacity weighting method, and a dynamic equivalent model of wind farm is obtained. Simulation results carried on a real wind farm indicate that the obtained model can describe the dynamic response characteristics of the wind farm with the accuracy close to the detailed model. Keywords： dynamic gray correlation analysis； cluster algorithm； wind farm； wind turbine grouping； dynamic equivalence

10.11830/ISSN.1000-5013.201702016

2016-04-29

方瑞明(1972-)，男，教授，博士，主要从事电力设备在线监测与故障诊断的研究.E-mail:fangrm@126.com.

国家自然科学基金资助项目(51577050)； 福建省厦门市重大科技创新平台资助项目(3502Z20111008)； 华侨大学研究生科研创新能力培育项目(1400201013)

TM

A

1000-5013(2017)02-0218-07