紧急制动工况下车辆的PI稳定性控制

李军， 方春杰, 束海波

(重庆交通大学 机电与车辆工程学院， 重庆 400074)

紧急制动工况下车辆的PI稳定性控制

李军， 方春杰, 束海波

(重庆交通大学 机电与车辆工程学院， 重庆 400074)

针对制动工况中的汽车，建立9自由度车辆动力学模型，并基于车辆动力学模型，采用比例-积分(PI)稳定性控制逻辑算法对车辆的行驶状况及运动姿态进行控制.最后，利用CarSim和MATLAB/Simulink联合仿真平台，结合低附着系数路面和对开路面的紧急制动工况进行离线仿真.仿真结果表明：采用稳定性控制逻辑算法可以改善车辆的纵向运动状态，有效地抑制车辆的侧向运动，有助于提高车辆的稳定性. 关键词： 车辆； 对开路面； 紧急制动； 稳定性控制； 动力学模型

高速行驶的车辆在行驶方向上遇到突发状况时，需要进行紧急制动.当前、后车轮均位于低附着系数路面时，车辆不能充分利用制动系统提供的制动力，前、后车轮极易发生抱死，致使车辆失去转向能力，造成车辆制动效能下降，车辆的制动距离大幅度增加.若左、右两侧车轮分别处于附着系数相差较大的对开路面，两侧车轮产生的地面制动力相差较大，导致车辆受到较大的横摆力矩作用而发生甩尾甚至激转[1]，偏离其预定的行驶车道，将危及乘员的人身安全.针对紧急制动工况下的车辆稳定性控制问题，研究人员陆续提出了诸多控制方法.赵伟等[2]提出利用主动转向技术控制汽车紧急制动时的稳定性；唐国元等[3]采用最优控制方法解决车辆在对开路面制动时的稳定性问题；晏蔚光等[4]提出一种结合横摆力矩控制和主动前轮转向控制，提高紧急制动侧偏稳定性的控制方法.本文针对四轮驱动汽车，建立9自由度车辆动力学模型，并在建模的基础上，采用稳定性控制逻辑算法对车辆的行驶状况及运动姿态进行控制.然后，利用CarSim和MATLAB/Simulink对车辆在低附着系数路面和对开路面上的紧急制动工况进行联合仿真，以验证控制的有效性.

1 车辆动力学建模

1.1 车辆动力学模型

为了反映车辆在紧急制动工况的运动状态及动力学特性，建立9自由度车辆动力学模型，如图1所示.9自由度依次为车辆的纵向运动、侧向运动、横摆运动、侧倾运动、俯仰运动，及前、后4个车轮绕各自车轴的转动自由度[5-9].

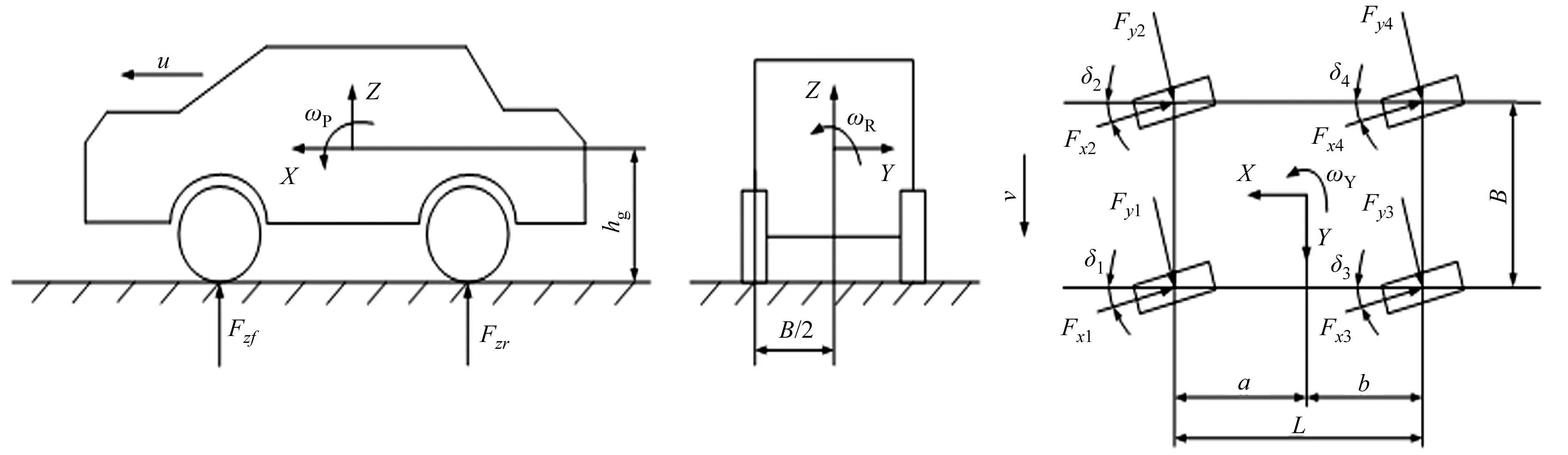
图1 9自由度车辆动力学模型Fig.1 Nine-degree-of-freedom vehicle dynamics model

建模过程中，主要考虑由纵向、侧向加速度引起的轴荷转移和轮胎的非线性动力学特性[9].该模型不考虑垂向自由度及悬架系统的影响.根据达朗贝尔原理，列出车辆动力学方程为

(1)

(2)

(3)

(4)

(5)

制动工况下，前、后4个车轮的转动方程为

(6)

车辆质心侧偏角为

(7)

1.2 轮胎动力学模型

采用“魔术公式”轮胎模型[10]，以滑移率、轮胎侧偏角和轮胎垂直载荷作为模型的输入，并以轮胎的纵向力、侧向力作为模型的输出.则该模型的表达式为

(8)

式(8)中：y(x)为纵向力或侧向力；x为滑移率或轮胎侧偏角；B为模型刚度因子；C为模型形状因子；D为模型峰值因子；E为模型形状因子.

1.3 车轮滑移率和轮胎侧偏角及其垂直载荷

车轮滑移率为

(9)

轮胎侧偏角为

(10)

一般地，车轮中心的纵向速度uw≈u，车轮中心的侧向速度vw≈vy.取重力加速度g=9.8m·s-2，则左前、右前、左后及右后轮胎的垂直载荷分别为

(11)

2 车辆稳定性控制

采用CarSim建立包含9自由度车辆动力学模型和“魔术公式”轮胎模型的整车模型，提出基于制动工况下汽车运动状态反馈的PI稳定性控制算法，其具体框架如图2所示.在图2中，利用CarSim整车动力学模型输出的纵向车速u、转向盘转角δsw等参数，由二自由度操纵参考模型[11]计算出理想的横摆角速度ωY_ideal为

(12)

式(12)中：K为稳定性因数，s2·m-2；i为转向系传动比.

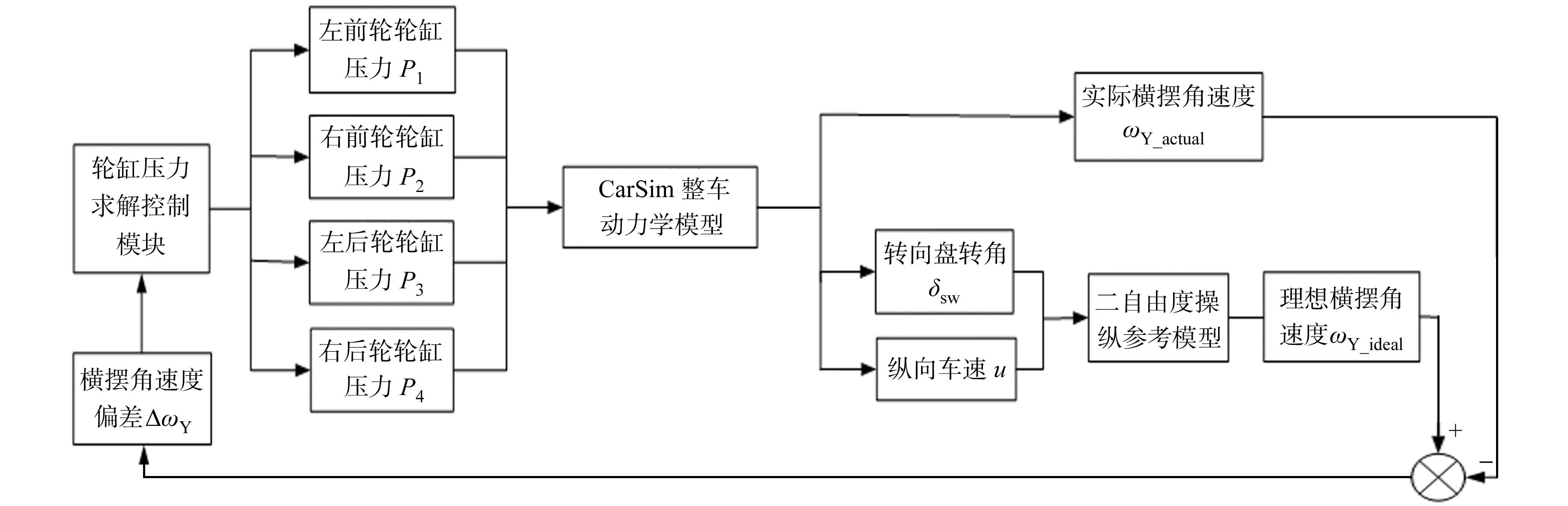
图2 稳定性控制算法的框架图Fig.2 Frame diagram of stability control algorithm

由车辆动力学模型计算出实际的横摆角速度ωY_ideal，从而得到横摆角速度偏差为

(13)

然后，利用ΔωY确定车辆4个车轮轮缸的制动压力，则可得到

(14)

式(14)中:Pi为第i个车轮的轮缸压力，MPa；T为换算系数；KP为比例环节系数；KI为积分环节系数；Δ为制动管路压力的动态修正量，MPa；Ci为第i个车轮的轮缸压力分配系数.

轮缸压力应位于最小调节压力Pmin和最大调节压力Pmax之间.当轮缸压力低于最小调节压力时，控制模块输出的轮缸压力值为零，此时,制动不起作用；当轮缸压力超过调节压力上限时，控制模块输出的轮缸压力值为最大调节压力Pmax.

图3 车辆稳定性仿真模型Fig.3 Vehicle stability simulation model

将各车轮的轮缸压力值反馈给CarSim整车动力学模型，使其输出横摆角速度、纵向车速和转向盘转角的数值；然后，将它们作为稳定性控制的输入，通过图2的控制算法框架实现轮缸压力的反复控制，从而不断调节施加于车辆各车轮的制动力，获得所需要的横摆角速度、质心侧偏角和制动距离等稳定性参数的期望值.

3 车辆稳定性仿真分析

采用Carsim和MATLAB/Simulink建立包含车辆整车动力学模型和稳定性控制器的仿真模型，如图3所示.为了验证车辆稳定性的控制效果，选取某款国产SUV车型，其具体配置参数,如表1所示；然后，结合低附着系数路面,对开路面下的两种紧急制动工况进行仿真.

表1 车辆具体配置参数

3.1 低附着系数路面下的紧急制动

车辆以70 km·h-1的初速度行驶2 s后紧急制动，路面附着系数为0.2.采用该工况进行仿真，得到引入稳定性控制前、后的车辆纵向车速、各车轮轮速变化曲线,如图4所示.图4(b)中各曲线的局部放大情况,如图5所示.图4,5中：v为速度；t为时间.

(a) 控制前 (b) 控制后图4 车辆纵向车速和各车轮轮速变化曲线Fig.4 Curves of vehicle longitudinal speed and each wheel speeds′ variation before control

由图4(a)可知：车辆在2 s时完成紧急制动，由于路面附着系数很低，各车轮的制动力立即增加并达到附着力，前左、前右、后左及后右4个车轮均发生抱死现象，其轮速立刻减小为零，此时，车辆完全失去转向能力.由图4(b)和图5可知：车辆的纵向速度与各车轮的轮速基本保持一致，由式(9)得到车轮的滑移率非常接近于零，此时，各车轮运动均接近于纯滚动状态.

在上述工况其他条件不变的前提下，将路面附着系数提高至0.8，通过对比仿真，得到未施加控制的两种不同附着条件下车辆的制动距离(S)，如图6所示.由图6可知：车辆在附着系数为0.2和0.8的两种路面上，2 s后发生紧急制动时的制动距离分别为89.26，24.06 m.显然，处于低附着条件下，未施加任何控制的车辆制动效能大幅度下降，制动距离显著增加.

图5 图4(b)中各曲线的局部放大图 图6 两种附着条件下车辆的制动距离 Fig.5 Partial enlargement of each Fig.6 Braking distance of vehicle curves in figure 4(b) under two adhesion conditions

综合上述分析可知，在紧急制动工况下，处于低附着系数路面的车辆在未施加任何控制时，车轮极易发生抱死现象，制动效能大幅降低.施加控制后的车辆在相同工况条件下，车轮运动接近于纯滚动状态，且车速有所下降.当在行驶方向上突遇障碍物时，由于前轮抱死无法进行转向操作，且制动距离较长，因而，未施加控制的车辆极易与障碍物发生碰撞，进而引发交通事故.相反，引入控制后的前轮均未发生抱死，因而，车辆可以通过适当转向有效地避开障碍物，从而避免事故的发生.

3.2 对开路面下的紧急制动

车辆在对开路面上以70 km·h-1的初速度行驶2 s后紧急制动，左侧车轮位于附着系数为0.2的低附着路面，右侧车轮则位于附着系数为0.8的高附着路面.基于该工况，仿真得到施加控制前、后车辆的运行轨迹，如图7所示.图7中：X为纵向位移；Y为侧向位移.由图7可知：在未施加控制时车辆侧向位移绝对值最大为6.59 m，施加控制后车辆侧向位移绝对值最大为0.273 m.

控制前、后的车辆横摆角速度(ωY)变化曲线，如图8所示.由图8可知：未施加控制的车辆横摆角速度波动较大，其绝对值最大为2.91 rad·s-1，施加控制后车辆的横摆角速度接近于零，其绝对值最大为4.82×10-4rad·s-1.通过对比可得，控制后车辆的横摆角速度显著减小.

图7 控制前、后的车辆运行轨迹 图8 控制前、后的车辆横摆角速度Fig.7 Vehicle running track before and after control Fig.8 Vehicle yaw rate before and after control

图9 控制前、后的车辆质心侧偏角Fig.9 Vehicle slip angle before and after control

控制前、后的车辆质心侧偏角(β)变化曲线，如图9所示.由图9可知：在整个紧急制动工况下，未施加控制的车辆质心侧偏角变化十分剧烈，其绝对值最大为3.14 rad，施加控制后车辆质心侧偏角显著减小，其绝对值最大为1.30×10-4rad.

综合上述分析可知，未施加控制的车辆在紧急制动过程中运动姿态急剧发生改变，侧向位移较大，行驶状态极不稳定；施加控制后，车辆的侧向位移、横摆角速度及质心侧偏角均显著减小，其侧向运动得到了有效地抑制，行驶状态得到了良好地调整，表明控制取得了较好的效果.

4 结束语

针对制动工况下的汽车，建立了9自由度车辆动力学模型，采用稳定性控制逻辑算法，根据理想、实际横摆加速度的差值对各车轮轮缸压力进行调节，进而实现对各车轮制动力的控制.结合低附着系数路面、对开路面下的两种紧急制动工况进行仿真.结果表明:该控制方法可以较好地调整车辆的运动姿态，改善了车辆的纵向行驶状态，有效地抑制了车辆的侧向偏移，对提高汽车的稳定性和行驶安全性具有一定的作用.

[1] 赵伟，魏朗，杜峰.基于模糊-PID控制的对开路面汽车制动稳定性研究[J].河北工业大学学报，2008，37(1):48-50.

[2] 赵伟，魏朗，周志立,等.基于主动转向技术的汽车制动稳定性控制[J].农业机械学报，2008，39(2):33-38.

[3] 唐国元，宾鸿赞.对开路面制动车辆稳定性的控制方法及仿真[J].计算机仿真，2007，24(3):254-256.

[4] 晏蔚光，毋茂盛，余达太,等.一种基于横摆力矩和主动前轮转向控制的制动稳定性控制方法[J].北京科技大学学报，2005，27(4):505-508.

[5] 王国业，张彦如，章娟丽,等.基于非平稳约束试验系统的汽车附着极限稳定性研究[J].农业机械学报，2012，43(8):1-3.

[6] 赵艳娥,张建武.基于滑模控制的四轮驱动电动汽车稳定性控制[J].上海交通大学学报,2009,43(10):1526-1528.

[7] 徐明法.基于最优滑模控制理论的车辆稳定性控制策略研究[D].长春：吉林大学,2011:7-10.

[8] 张对霞.汽车ESC硬件在环仿真研究与试验[D].秦皇岛：燕山大学，2013：13-15.

[9] 赵治国，顾君，余卓平.四轮驱动混合动力轿车驱动防滑控制研究[J].机械工程学报，2011，47(14):86-88.

[10] PACEJKA H B，BESSELINK I J M.Magic formula tyre model with transient properties[J].Vehicle System Dynamics，1997，27(S1):13-29.

[11] 喻凡，林逸.车辆系统动力学[M].北京：机械工业出版社，2008:200-205.

(责任编辑： 黄晓楠 英文审校： 崔长彩)

PI Stability Control of Vehicle Under Emergency Braking Conditions

LI Jun， FANG Chunjie, SHU Haibo

(School of Mechantronics and Vehicle Engineering， Chongqing Jiaotong University， Chongqing 400074， China)

In this paper, a nine-degree-freedom dynamic model was built and a proportional integral (PI) stability control logic algorithm was applied to control vehicles driving conditions and postures under the conditions of emergent braking. Off-line simulations were performed using CarSim and MATLAB/Simulink software to study the effects of low adhesion coefficient road and bisectional road during the emergency braking condition. Simulation results demonstrated that the stability control logic algorithm can improve the vehicle longitudinal motion state and effectively inhibit undesirable lateral movement of vehicle which contributes to enhancing the vehicle stability. Keywords： vehicle； bisectional road； emergency braking； stability control； dynamics model

10.11830/ISSN.1000-5013.201702001

2016-09-29

李军(1964-)，男，教授，博士，主要从事汽车发动机排放与控制、节能与新能源汽车的研究.E-mail:cqleejun@163.com.

重庆市自然科学基金重点项目(CSTC2013yykfB0184)； 重庆市教委科技项目(KJ120423); 重庆市重点实验室项目(csct2015yfpt_zdsys30001)

U 463

A

1000-5013(2017)02-0135-06