受扰线性不确定系统鲁棒H∞混合镇定
庄梁, 林灿煌, 孙洪飞
(厦门大学 航空航天学院, 福建 厦门 361005)

受扰线性不确定系统鲁棒H∞混合镇定
庄梁, 林灿煌, 孙洪飞
(厦门大学 航空航天学院, 福建 厦门 361005)
针对受外界扰动和参数不确定性影响的线性系统,同时考虑其暂态性能和稳态性能,提出基于混合稳定的鲁棒H∞控制概念和控制方法.给出闭环系统混合稳定且抑制外部扰动对被控输出影响的充分条件,并将这些条件转化为线性矩阵不等式约束.所设计的是一个关于时间连续的H∞混合镇定控制器,简化了设计过程,避免控制器切换导致的抖振.仿真结果表明:在外界扰动和参数不确定影响的情况下,该控制方法达到预期的暂态性能和稳态性能的要求,且有效抑制了干扰对系统状态的影响. 关键词:H∞混合镇定控制器; 鲁棒H∞控制; 线性不确定性系统; 外界扰动; 闭环系统
在实际应用中,除了研究控制系统的稳态性能[1]外,更加注重的是控制系统能否满足相应的暂态性能指标要求[2].为了研究系统的暂态性能,Dorato首先提出了“短时间稳定性”的概念,即后来所谓的有限时间稳定(finite-time stable,FTS),并得到学术界的广泛关注和研究.有限时间稳定要求在给定时间区间内,系统的状态始终不超过给定界限[3-4].有限时间稳定和李亚普若夫渐近稳定(Lyapunov asymptotic stability,LAS)是两个互相独立的概念[5].对于控制过程比较短暂的系统,如机器人操控系统、导弹系统等,除了研究控制系统的稳态性能外,更加注重的是控制系统能否满足相应的暂态性能指标要求.林灿煌等[6]研究了输入受限不确定线性系统的镇定问题,并首次提出了混合稳定的概念,给出混合稳定的稳定性条件.目前,控制系统扰动抑制采用的控制策略主要有内模原理[7]、滑模控制[8-10]、自适应干扰抑制[11]和H∞控制理论[12-13].申铁龙[12]在控制器设计过程中不仅能实现对干扰的抑制,且考虑了系统数学模型在一定范围内存在的不确定性影响.Sun等[13]通过H∞控制和非线性干扰观测器解决了系统含有周期扰动时的控制问题.本文针对受外界扰动和参数不确定性影响的线性系统,同时考虑系统控制过程中的暂态性能和稳态性能,提出一种基于混合稳定的鲁棒H∞控制概念和控制方法.
1 问题描述
考虑如下受扰线性不确定系统
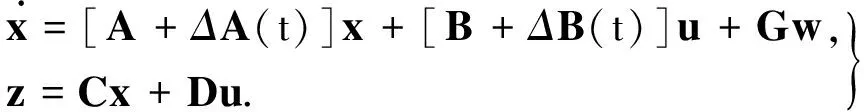
(1)
式(1)中:x∈Rn为系统的状态变量;z∈Rp为系统的被调输出;u∈Rm为系统的控制向量;w∈Rq为能量有限的外部干扰信号;A∈Rn×n,B∈Rn×m,G∈Rn×q,C∈Rp×n,D∈Rp×m为描述标称系统的矩阵.ΔA,ΔB是系统的不确定参数矩阵并假设它们是范数有界的,则有形式[14]为
(2)
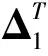
外部扰动条件应满足
(3)
定义1[3]考虑如下线性系统,有
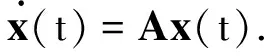
(4)
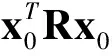
则称该系统关于(c1,c2,T,R)是有限时间稳定的,其中,x0=x(0)是系统的初始状态.
定义2[6]如果系统(4)关于(c1,c2,T,R)是有限时间稳定的,且在无穷时间区间上是李雅普诺夫渐近稳定(LAS)的,则称系统是混合稳定的.
问题1 (H∞混合镇定)对系统(1)设计一个状态反馈控制器,即
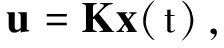
(5)
使得系统(1)连同控制器(5)形成的闭环系统.a) 当w=0时,混合稳定;b) 当x(0)=0时,从外部扰动w到被控输出中z的L2增益小于给定正数γ.K为需要设计的控制器增益矩阵,称具有性质a)和b)的控制器u为H∞混合镇定控制器.
2 H∞混合镇定控制器设计
混合控制需要同时考虑系统的暂态性能和稳态性能.文献[6]给出的混合控制器本质上包含两部分,暂态过程控制器u1=K1x和稳态过程控制器u2=K2x,其中,K1,K2为控制器增益矩阵.控制器u1的作用是使闭环系统满足暂态过程性能要求,控制器u2的作用是使闭环系统满足稳态过程性能要求.一般的混合控制器的形式为
(6)
上述混合控制器是关于时间的切换控制器,在t=T时刻,由于控制输入的不连续性会导致系统状态出现跳变甚至抖振.文献[6]通过引入缓冲时间消除潜在抖振,得到控制器形式为
(7)
式(7)中:ts为切换缓冲时间;k=K1+(K2-K1)(t-T)/ts为过渡时间段控制器增益矩阵.
仿真结果表明:通过引入缓冲时间可以在一定程度上消除抖振,但无法在理论上保证闭环系统混合稳定.以下给出控制器简化的设计过程,所设计关于时间连续的H∞混合镇定控制器使H∞混合镇定问题1可解.
引理1[15]给定适当维数的矩阵N,E和M,其中,N是对称的,则
对所有满足ΔT(t)Δ(t)≤I的矩阵Δ(t)成立,当且仅当存在数ε>0,使
下面定理通过给出一个关于时间连续的H∞混合镇定控制器,使当系统受到外界干扰和不确定影响时,满足有限时间稳定和渐近稳定.
定理1 如果存在标量α≥0,γ>0,ε>0,矩阵L∈Rn×m和正定对称矩阵Q∈Rn×m,使
(8)
(9)
(10)
式(10)中:A1=A+ΔA+(B+ΔB)K,且有
(11)
另一方面,由Schur补引理可知,式(8)等价于
(12)

(13)
再由引理1可知,式(13)等价于
(14)
式(14)中:C1=C+DK.
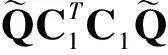
(15)
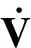
(16)
对式(16)从 0到t积分,∀t∈[0,T],可得
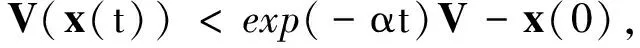
(17)
则有
(18)
又因xTR1/2Q-1R1/2x(t)≥λmin(Q-1)x(t)TRx(t),则λmin(Q-1)x(t)TRx(t)≤xTR1/2Q-1R1/2x(t)≤exp(αT)[λmax(Q-1)x(0)TRx(0)],由此可得
(19)
则有
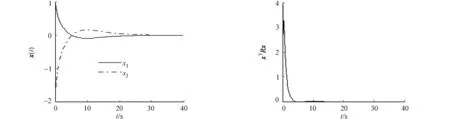
再由式(9)可得x(t)TRx(t) 因此,当外扰为零时,闭环系统在时间[0,T]上有限时间稳定,在无穷时间内渐近稳定,即当外扰为零时,闭环系统混合稳定. (20) 对比式(11)和式(20)可得 (21) 两边对式(21)积分,可得 (22) (23) 即‖z‖<γ‖w‖.故x(0)=0时,从外部扰动w到被控输出z的L2增益小于γ. 注1 文献[6]中使用的是两个不同的李雅普诺夫函数,分别刻画系统的有限时间稳定和渐近稳定性;而定理1中使用的是一个李雅普诺夫函数,同时刻画系统的有限时间稳定和渐近稳定性,具有一定的保守性.定理1给出的H∞混合镇定控制器是一个关于时间连续的控制器,简化了设计过程,避免了控制器切换过程存在的潜在抖振. 由定理1可知,式(8)是一个线性矩阵不等式形式,而式(9)不是线性矩阵不等式形式.为了方便控制器求解,将定理1转化为如下基于线性矩阵不等式(LMI)的可行解问题. 推论1 如果存在标量α≥0,γ>0,ε>0,矩阵L∈Rm×n和正定对称矩阵Q∈Rn×n,使式(8)和下列LMI成立,即 (24) 考虑外界干扰和不确定影响,设计H∞混合镇定控制器,将得到的控制器在线性系统上进行仿真.使过渡时间在10s内,超调量不超过10%,系统状态稳定到平衡点且对外界干扰有一定的抑制作用. 假设受控系统(1)参数为 ΔA,ΔB分别满足‖ΔA‖≤0.1,‖ΔB‖≤0.1,将不确定性矩阵ΔA,ΔB写成式(2)形式,其中 状态变量的初值为 给定的外部扰动具有衰减特性,由如下线性系统描述 为了实现控制目的,取(c1,c2,T,R)=(1,4,10,I2×2),给定α=0.2,γ=1.3.由推论1可得H∞混合镇定控制器u=Kx,其中,K=[-1.355 760 0 -1.013 010 4].将得到的控制器在本节给出的线性系统上进行仿真,仿真结果如图1,2所示. 图1 系统状态变化曲线 图2 xTRx变化曲线图 Fig.1 Curves of state Fig.2 Curves of xTRx 为了说明H∞混合控制器的优越性,对给出的系统分别使用H∞混合镇定控制器、渐近控制器[15]、混合稳定控制器[6]进行仿真.其中:H∞渐近控制器增益矩阵K渐近=[-2.796 947 3 -7.591 343 0];混合稳定控制器中的有限时间稳定控制器增益矩阵K1=[-1.097 713 1 -2.865 556 4];渐近稳定控制器增益矩阵K2=[-3.526 577 2 -7.020 336 6].在H∞混合镇定控制器和H∞渐近控制器作用下,系统状态1的变化曲线,如图3所示.在H∞混合镇定控制器和混合稳定控制器作用下,系统状态1的变化曲线,如图4所示. 图3 使用H∞ 混合镇定控制器和 图4 使用H∞混合镇定控制器和混H∞渐近控制器系统状态1变化曲线 稳定控制器系统状态1变化曲线Fig.3 Curves of state under H∞ mixed Fig.4 Curves of state under H∞ mixed stabilization controller and H∞ asymptotic controller stabilization controller and mixed controller 由图3,4可知:系统在受到外界扰动和不确定影响的情况下,系统状态最终能稳定到平衡点,超调量小且系统的状态不超过给定的界限.由图3可知:单独使用渐近控制器,系统状态稳定到平衡点过渡时间长,超调量大.由图4可知:H∞混合镇定控制器相对于一般的混合稳定控制器能有效抑制干扰对系统状态的影响.这说明设计的H∞混合镇定控制器的有效性和优越性,保证了系统的暂态性能和稳态性能要求,且对外界扰动有一定的抑制作用. 针对受外界扰动和参数不确定性影响的系统,提出了基于混合稳定意义下的鲁棒H∞控制方法.同时考虑系统的暂态性能和稳态性能,给出了闭环系统混合稳定且抑制外部扰动对被控输出影响的充分条件,将这些条件转化为线性矩阵不等式约束.本文设计的H∞混合镇定控制器是一个关于时间连续的函数,简化了控制器设计过程.如何将文中结果应用于不仅需要满足稳态性能指标要求,而且需要满足相应暂态性能指标要求的系统,如机器人操控系统、导弹系统、宇航控制系统等控制过程比较短暂的实际系统,有待于进一步研究. [1] KHALIL H K,GRIZZLE J W.Nonlinear systems[M].New Jersey:Prentice Hall,1996:112-118. [2] AMATO F,AMBROSINO R,ARIOLA M,etal.Finite-time stability and control[J].London:Springer,2014:9-17. [3] AMATO F,CARANNANTE G, DE TOMMASI G,etal. Necessary and sufficient conditions for input-output finite-time stability of linear time-varying systems[C]∥IEEE Conference on Decision and Control and European Control Conference.Orlando:IEEE Press,2011:1933-1937. [4] DORATO P.Short-time stability in linear time-varying systems[C]∥Proceedings of the IRE International Convention Record.New York:IEEE Press,1961:83-87. [5] AMATO F,ARIOLA M,DORATO P.Finite-time control of linear systems subject to parametric uncertainties and disturbances[J].Automatica,2001,37(9):1459-1463. [6] 林灿煌,孙洪飞.输入受限不确定线性系统混合镇定[J].厦门大学学报(自然科学版),2016,55(2):244-250. [7] LU Jin,BROWN L J.A combination of open and closed-loop control for disturbance rejection[C]∥24th Canadian Conference on Electrical and Computer Engineering.Niagara Falls:IEEE Press,2011:563-568. [8] TANG Gongyou,LU Shanshan,DONG Rui.Optimal sliding mode control for linear time-delay systems with sinusoidal disturbances[J].Journal of Sound and Vibration,2007,304(1/2):263-271. [9] YOUNG K D,UTKIN V I,OZGUNER U.A control engineer′s guide to sliding mode control[J].IEEE Transactions on Control Systems Technology,1999,7(3):328-342. [10] NA S,LIBRESCU L,KIM M.H,etal.Robust aeroelastic control of flapped wing systems using a sliding mode observer[J].Aerospace Science and Technology,2006,10(2):120-126. [11] FUENTES R J,BALAS M J.Direct adaptive rejection of persistent disturbances[J].Journal of Mathematical Analysis and Applications,2000,251(1):28-39. [12] 申铁龙.H∞控制理论及应用[M].北京:清华大学出版社,1996:121-124. [13] SUN Haibin,HOU Linlin,ZONG Guangdeng.Asymptotic attenuation and rejection for systems with general periodic disturbances via nonlinear disturbance observer andH∞, control[C]∥Proceedings of the 34th Chinese Control Conference.Hangzhou:IEEE Press,2015:710-715. [14] QIAN Chengshan,WU Qingxian,JIANG Changsheng,etal.H∞tracking control for a class of uncertain nonlinear systems with time-delay by using multi-model switching[J].Journal of Shandong University,2008,42(12):4150-4154. [15] 俞立.鲁棒控制: 线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:87-88. (责任编辑: 钱筠 英文审校: 崔长彩) RobustH∞Mixed Stabilization of Uncertain Linear Systems With Disturbances ZHUANG Liang, LIN Canhuang, SUN Hongfei (School of Aerospace Engineering, Xiamen University, Xiamen 361005, China) To guarantee both the transient and steady performances of a linear system with uncertainties and disturbances, a new control method called mixed-stability-basedH∞stabilization is proposed. The solvable conditions of mixed-stability-basedH∞stabilization are presented by using the linear matrix inequalities. The mixed-stability-basedH∞stabilization controller given in this paper is continuous in time domain, thus simplifies the design process and avoids the potential chattering. Finally, a numerical simulation is conducted to demonstrate the effectiveness and feasibility of the proposed method. Keywords:H∞hybrid stabilization controller; robustH∞control; linear uncertain system; external disturbance; closed loop system 10.11830/ISSN.1000-5013.201702003 2016-08-02 孙洪飞(1970-),男,教授,博士,主要从事混合系统控制、基于网络的系统控制和非线性控制理论及在运动体控制上的应用的研究.E-mail:sunhf@xmu.edu.cn. 国家自然科学基金资助项目(61273153, 61374037) TP 273 A 1000-5013(2017)02-0147-06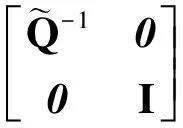
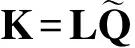
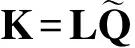
3 数值仿真
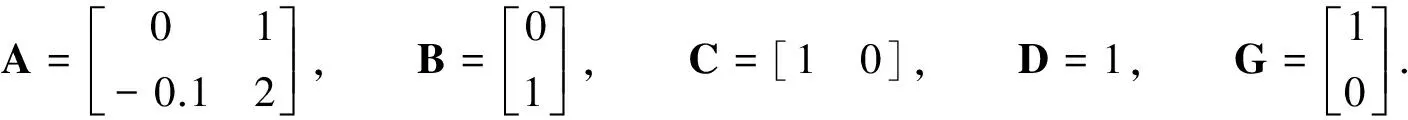
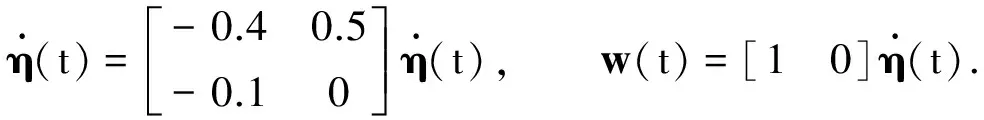

4 结束语

