基于共同题非等组设计的等值结果评价标准研究综述
张健 任杰
(北京语言大学,北京 100083)
等值是将同一测验不同版本的分数统一到一个量尺上的过程[1]。经过等值的分数才可以直接比较,因此,等值是测验公平性和科学性的重要保障。为了实现同一测验不同版本分数的可比性,目前国内外许多大型标准参照测验均对测验分数进行了等值处理。标准参照测验是以具体体现教学目标的标准作为依据,确定学生是否达到标准以及达标的程度如何的一种评价方法,即“人与标准比较”的方法,它是衡量学生能做什么的绝对评价。
在我国,大学英语四、六级考试(CET-4,CET-6),少数民族汉语水平等级考试(MHK)等均属于标准参照测验。对于这类测验而言,其标准是长期稳定的,但是其不同年份的试卷难度和考生能力很难保证完全相同。就难度而言,尽管命题专家在命题过程中尽力保持考试难度的稳定性,但是不同试卷之间在难度、分数分布方面的差别还是在所难免的。这种差别不仅会影响到考试的质量,也会影响评价标准的客观性。为了将不同年份的试卷置于同一个量尺上并用同一标准比较,需要对不同试卷进行等值处理。此外,随着我国高考外语“一年两考”模式的开启,作为常模参照测验的高考英语也面临着同样的问题。常模参照测验是将考生测验分数与其所在考生群体进行比较,即“人与人比较”,但同一年份的两份高考英语试卷很难保证难度完全一致,这使得作答较难试卷的考生处于劣势,直接影响高考英语的公平性。因此,无论是标准参照测验还是像高考英语这样的常模参照测验,都需要经过等值技术将不同试卷置于同一量尺上,最终实现不同试卷分数的可比性。近年来,虽然等值技术在我国已得到广泛应用,如CET-4、CET-6、MHK等,但不同研究者对等值结果的评价标准却不尽相同。谢小庆使用总平均加权差异平方和(MSD)对HSK的等值结果进行评价[2],焦丽亚使用变异均方根(RMSD)对湖南某地区中考数学成绩的等值结果进行评价[3]。此外,还有学者采用模拟检验、跨样本一致、标准误、重要差异等方式评价等值结果[4-7]。这些等值结果评价标准的区别是什么?它们的使用条件是否相同?对于具体的测验而言应该选用哪种标准?目前学界对这些问题的探讨还远远不够,这可能导致由于评价标准的不同,使得不同研究者对同一等值结果的解释大相庭径,直接影响研究结论的可信度。因此,只有深入地认识等值结果的评价标准,才能根据实际需要选择合适的标准并对等值结果进行合理评价,使等值技术真正落到实处。
1 等值误差
对等值结果的评价本质上是对等值误差的评价。等值过程中存在着两类误差,一类是随机误差,一类是系统误差。随机误差来源于样本,可以通过增加样本量来减少;系统误差远比随机误差复杂,原因主要有:研究违背了等值方法的统计假设或数据收集原则,一些等值技术的使用无形中引入了系统误差等。针对等值过程中存在的误差,研究者们提出了一系列评价标准,然而,没有一个等值结果评价标准可以应用到所有的等值情境中[8]。对于经典测量理论(CTT)等值而言,经过等值可以得到分数的等值结果;对于项目反应理论(IRT)等值而言,经过等值不仅可以得到分数等值的结果,还可以得到参数等值的结果(包括项目参数等值结果和被试能力参数等值结果)。因此,我们根据评价对象的不同,将等值结果评价标准划分为以下两种类型:一类是用于评价等值分数的标准,另一类是用于评价等值参数的标准。下文将以共同题非等组设计为例,对该等值设计下的等值结果评价标准进行梳理,以期通过对比不同等值结果评价标准的原理、适用范围及其优缺点等,深化对等值结果评价标准的认识,并为研究者今后根据实际需要选择合理的评价标准提供借鉴。
2 等值分数的评价标准
2.1 共同组标准
在共同题非等组设计中,可以采用共同组作为标准对等值结果进行评价,共同题等值分数结果和共同组等值分数结果差异越小,则代表等值方法越优。计算指标上可以选用总平均加权差异平方和(MSD):
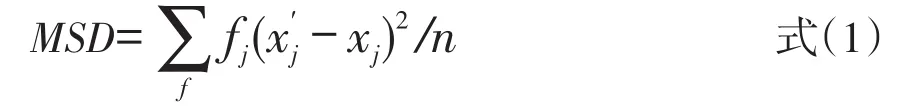
其中j是原始分数,是作为标准的共同组等值分数,xj是经过等值的分数,fj是获得原始分j的人数[2],且

这种方法虽然简单客观,但是也有其局限性。尤其是在大型标准化考试中很难找到满足条件的共同组,因为一次测验不可能让被试在短时间内同时考两次,即使能找到合适的被试,被试前后参加同一个测验的动机等因素也会直接影响等值效果。
2.2 等值分数的标准误
等值分数标准误是描述等值随机误差的指标。通过从总体中重复抽样,以一个完全拟合数据条件的等值方法进行等值,那么,等值结果分布的平均数即是真正的等值分数,而分布的标准差即是等值分数标准误[9]。戴海崎认为,采用Bootstrap法估计等值分数标准误比较接近于等值结果评价标准误的定义[10],并提出Bootstrap法估计等值分数标准误主要包括以下几个步骤:
1)从X测验一个容量为Nx的样本中有返回地随机抽取一个Bootstrap样本,容量为nx;
2)从Y测验一个容量为Ny的样本中有返回地随机抽取一个Bootstrap样本,容量为ny;
3)用相应的等值方法,在所抽取的两个Bootstrap样本上估计X与Y的等值关系,记为

重复步骤1)~3)R次,则获得R个等值关系式,即
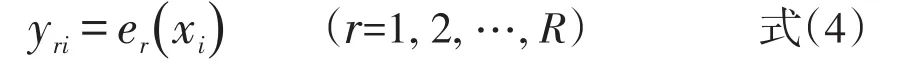
4)在R足够大情况下,用式(5)求出等值分数标准误的Bootsrap估计值
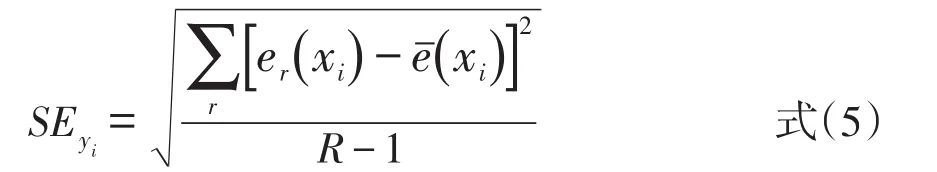
其中,
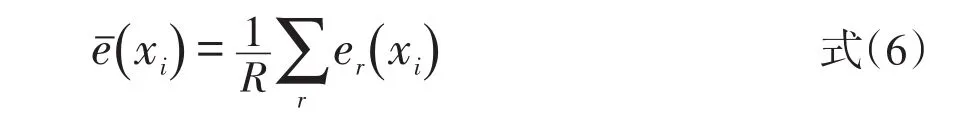
等值分数标准误是目前主流的对等值分数的评价标准,大量的研究均采用这种等值结果评价标准[11-14]。通过对等值分数标准误的估计原理分析,我们发现等值分数标准误的本质是考察等值分数受样本影响的大小,其假设是在样本不同的情况下,等值分数结果越稳定的方法越好。然而,在计算过程中,等值分数标准误也受到了样本量的影响,当样本量越大时,等值分数标准误越稳定,当样本量较少时,等值分数标准误的估计结果不稳定。因此,当样本量较小时,不建议采用等值分数标准误作为等值分数的评价标准。
2.3 重要差异
Dorans提出了一种重要差异(Differences That Matter)作为等值的评价标准。他认为,在特定分数点上,等值结果之间的差异大于0.5倍原始分数,则为两种方法有重要的差异[15]。这种重要差异的标准在SAT测验等值上已得到广泛应用。Brossman等用等百分位等值结果作为标准,采用重要差异的方法检验MIRT真分数法和观察分数法等值结果的稳定性[16]。由此可见,重要差异方法的本质是将一个新方法的等值分数结果与一个公认较好的方法的等值分数结果对比,以公认较好的方法的分数等值结果为标准,比较二者差异,差异越小,则说明新方法的等值效果越好,然而在现实中很难找到一个适用于不同等值情境的公认的较好方法。
2.4 跨样本一致性检验
跨样本一致性检验的基本原理是:由于抽样会带来随机误差,因此受样本的影响最小的等值方法就是最稳定、最优的等值方法。跨样本一致性检验的操作步骤如下:首先,将总体划分为几个样本,这几个样本之间互不包含;其次,用总体数据和样本数据分别进行等值;最后,比较样本等值结果与总体等值结果的差异,差异最小的方法即在不同样本中表现最为一致的方法就是较好的方法。跨样本一致性检验的计算采用REMSD指标,公式如下:
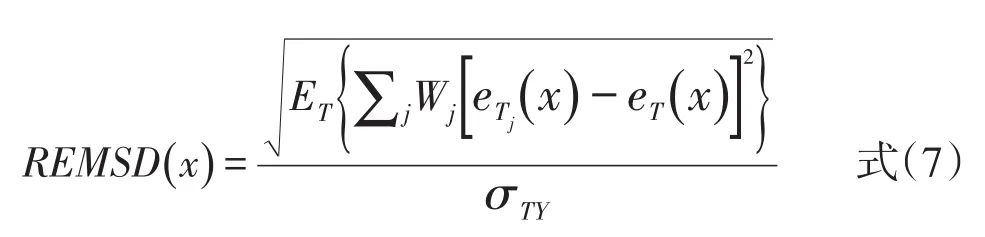
共同题非等组设计包含两个被试群体。T是由被试组P和被试组Q按照一定比例组成的综合组。Tj表示从综合组T中抽取出的小样本,公式中eTj(x)表示在综合组小样本Tj中将X卷分数等值到Y卷上的分数,eT(x)表示综合组T上X卷分数等值到Y卷上的分数。eTj(x)和eT(x)的等值方法相同。ET{ }是指T组在X卷上分布的平均数,Wj表示被试组P和被试组Q的权重[6]。另外,可以采用前述的重要差异标准判断REMSD结果是否在合理范围。跨样本一致性检验仅能描述等值方法受样本影响的程度,一种等值方法的跨样本一致性越高,表明用该方法等值时的随机误差越小,但是该方法对系统误差无法估计。
2.5 等值分数交叉检验
等值分数交叉检验的方法和跨样本一致性检验类似,也是以大样本所得的等值分数结果为标准,通过对比小样本等值分数结果与大样本等值分数结果的差异,差异最小的方法就是较好的方法。与跨样本一致性检验不同的是,交叉检验只选取大样本中的一部分小样本,仅涉及一个小样本群体。其计算公式是
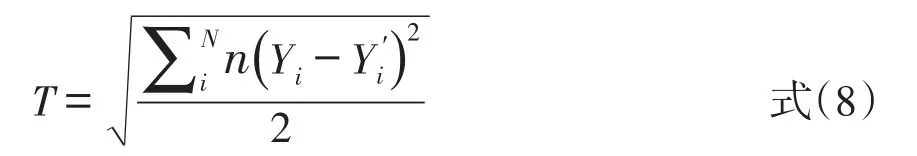
其中,Yi表示在等值分数交叉检验的样本中,将测验X上总分排在第i位的考生采用某种方法等值到测验Y上的实际分数,n是获得该分数的人数,Yi
'表示在大样本中将测验X上总分排在第i位的考生采用同种方法等值到测验Y上的实际分数,N是交叉验证样本的总人数。T指标的值越小,表明各等值方法所得结果的一致性越高[14]。和跨样本一致性检验一样,交叉检验方法也只能够选取出随机误差最小的等值方法,但对不同等值方法的系统误差的大小却无法估计。
3 等值参数的评价标准
3.1 共同题参数稳定性
在共同题非等组设计下,共同题是用于连接两个平行测验的桥梁。对于共同题参数而言,从理论上看,用分别校准法将新测验的共同题参数等值到基准测验上时,等值后的共同题参数应该是相同的,但实际由于等值误差的存在,使得经过等值后的共同题参数往往不一致。正因为如此,若经过某种等值方法等值后的共同题参数差别越小,则说明等值误差越小,等值方法越好。根据这一思路,研究者提出以RMSD作为分别校准法下评判项目参数等值方法精确性的操作性检验标准,以此衡量各种等值方法的误差大小[3]。RMSD计算公式如下:
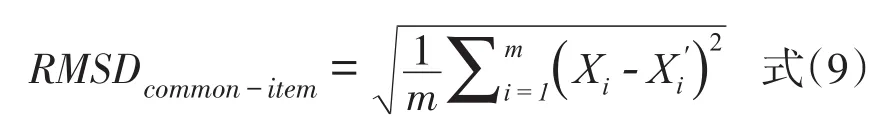
其中,m代表共同题的数量,Xi为作为基准测验的项目参数,X'i为新测验等值到基准测验上的项目参数。RMSD值越小,表明等值方法的等值误差越小,经过该等值方法等值后的共同题参数越稳定。共同题参数稳定性的估计中既包含了随机误差的大小,也包含了系统误差的大小,因此,相较而言,共同题参数稳定性的方法对等值误差的估计更全面。但是共同题参数稳定性方法的使用有一定的局限性,它仅适合对共同题非等组设计下采用分别校准法所得的参数等值结果进行评价,对于其他等值方法如同时校准法、固定校准法,则共同题参数稳定性指标无法适用,这也使得共同题参数稳定性指标的使用范围受到一定限制。
3.2 模拟研究参数返真性
在等值参数评价标准中,通过模拟研究观察参数的返真性是目前主流的评价标准,大量的研究均采用这种参数等值结果评价标准[4-5,17]。这种方法的操作步骤如下:首先,通过使用IRT模型估计基准测验X的参数(包括项目参数和能力参数)并给定等值系数A和B;其次,以测验X的参数结果和等值系数A和B为真值,采用Monte-Carlo法生成新的测验X′的数据来模拟测验X的作答情况;然后,估计新测验X′的项目参数和能力参数。再次,采用不同的等值方法将新生成的测验X′的参数重新等值到原始的基准测验X上;最后,以测验X的真实参数结果作为等值的标准,对比新测验X′等值后的参数结果和测验X的真实参数结果的差异,偏差越小代表等值效果越优,等值方法的参数返真性越好。
在具体研究中,通常采用以下两类指标衡量偏差的大小,一类是衡量项目参数返真性指标,另一类是衡量等值系数返真性指标。
3.2.1 均方根误差指标和偏差
均方根误差指标(RMSE)、偏差(BIAS)均采用X′等值后的难度、区分度参数和原来的X的难度、区分度参数对比。这里的参数仅指共同题等值前后的参数。计算公式如下:
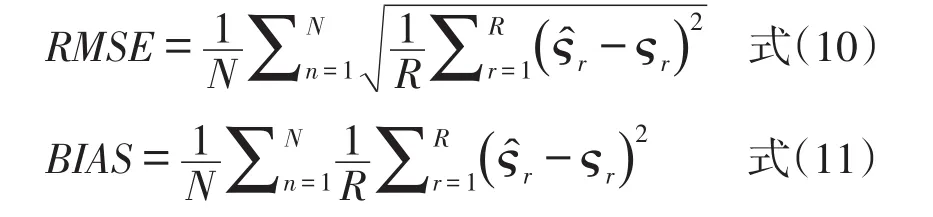
其中表示等值后的各参数,ςr表示参数的真实值,R表示全卷的题目数量,N表示重复的次数[4]。RMSE和BIAS的结果越小,代表等值后的共同题参数越接近真值,等值效果越好。
3.2.2 平均绝对离差
平均绝对离差(ABSE)表示的是等值系数真值与估计值的差异。其公式如下:
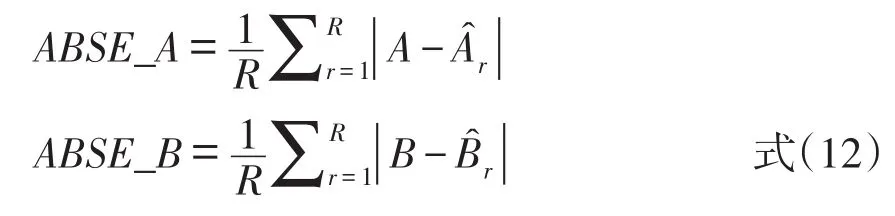
在式(12)中,R代表模拟实验的总次数,A和B表示等值系数真值,表示经过第r次模拟后的等值系数估计值,ABSE的值越小,代表等值系数估计值对真值的修复程度越好,即等值系数估计值越接近于真值。
尽管采用模拟研究观察参数返真性的方法是目前等值参数评价的主流方法,但也存在着一些问题,其最突出的问题是模拟数据与真实数据之间存在一定的差别,这对研究结果的使用产生很大制约。为了使模拟数据的结果更接近真实数据,研究者往往会进行多次模拟,一般而言,模拟次数不低于30次。
3.3 等值系数的标准误
基于IRT的等值主要包括两部分,第一部分是参数等值,包括项目参数等值和被试能力参数等值;第二部分是测验分数的导出,又分为IRT真分数法和IRT观察分数法两类。当有两个群体分别参加了两个测验X和Y,其中X是基准测验,Y是新测验,X和Y均有j道项目,且包含m个共同题(anchor item)。根据IRT等值理论,首先应进行测验X和Y的项目参数和被试能力参数的等值,测验X和Y的项目参数和能力参数具有如下关系[18]:

其中,A和B就是等值系数,IRT参数等值的核心就是求解等值系数A和B。正是由于求解等值系数A和B时所采用的估计参数的原理不同,才会产生不同的IRT等值方法。利用一种等值方法求解等值系数时,不仅会产生等值系数,还会产生等值系数估计的标准误,它是衡量等值系数受随机误差影响的程度。等值系数标准误越大,表明该等值方法的随机误差越大,等值结果越差。在应用方面,吴锐以等值系数估计的标准误为衡量标准,对IRT项目特征曲线法的等值结果进行分析[19]。但是,这种等值评价标准仅适用于IRT分别校准法,对IRT同时校准法和IRT固定校准法却不适用。
3.4 项目参数交叉检验
等值参数交叉检验方法和等值分数交叉检验的原理基本相同,即以大样本所得的参数等值结果为标准,通过对比小样本参数等值的结果与大样本参数等值结果的差异,差异最小的方法就是较好的方法。其计算公式是:
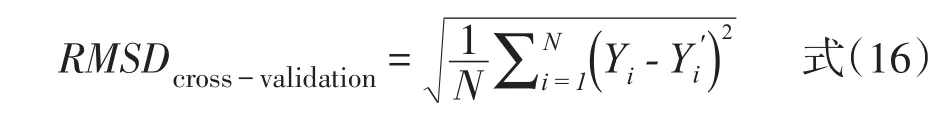
其中,Yi表示在交叉检验的样本中,Y测验上第i题等值后的项目参数,N表示测验的题目个数,Y'i表示在大样本中Y测验上第i题等值后的项目参数。RMSD指标的值越小,表明各等值方法所得结果的一致性越高[3]。等值参数交叉检验的方法仅适用于IRT等值,此外,等值参数交叉检验法也只能够选取出随机误差最小的等值方法,无法对等值方法的系统误差进行估计。
4 结语与建议
通过梳理国内外关于等值结果评价标准的文献,我们以共同题非等组设计为例,根据评价对象的不同,将等值结果的评价标准划分为两种类型:一类是用于评价等值分数的标准,一类是用于评价等值参数的标准,如表1所示。这两类标准既有联系又有区别,如交叉检验的标准既可以用于等值分数的评价也可以用于等值参数的评价,只是公式内容略有不同。而共同题稳定性的标准仅适用于等值参数的评价,重要差异的标准仅适合对等值分数结果进行评价。此外,我们对每种等值结果评价标准的适用范围及其局限性进行了简要说明,这将有助于研究者从宏观上把握等值结果评价标准的分类,并结合研究实际选择合理的等值结果的评价标准。
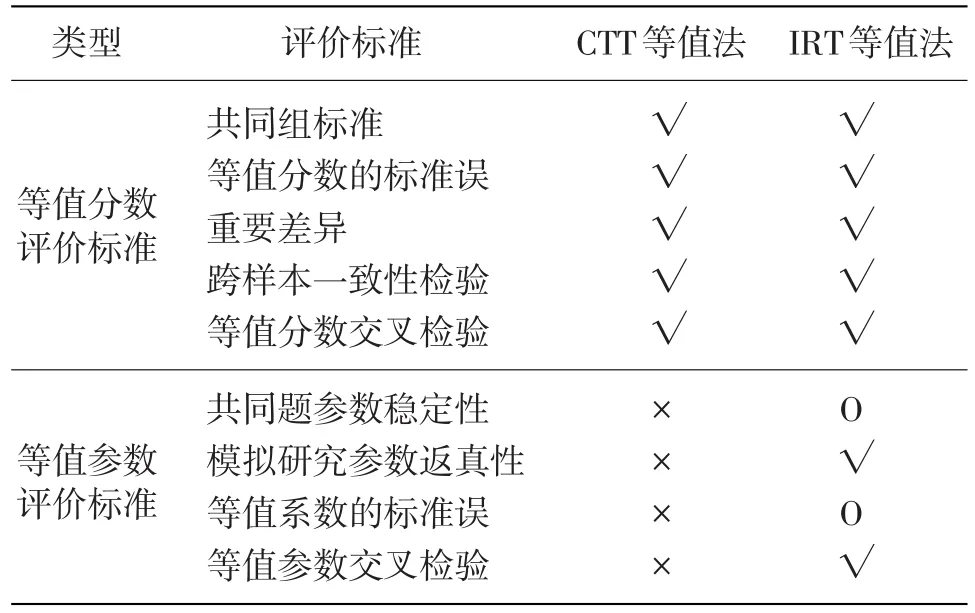
表1 等值结果评价标准概览
为此,我们提出以下建议:
第一,研究者可根据其等值研究所选用的等值方法的不同、等值结果的不同选择与其相对应的等值结果的评价标准。比如:若研究采用的是CTT等值方法,则只能选取用于评价等值分数的评价标准。
第二,以往的等值研究往往是采用一种标准对多种等值方法的结果进行评价,由于每种等值结果评价标准都有一定的局限性,仅仅采用一种标准对多种等值结果进行评价的做法过于绝对。因此,我们建议研究者可以根据研究对象的不同,采用多种评价标准对等值结果进行综合评价,从不同角度对等值结果进行合理解释,这不仅有助于深化研究者对各种等值方法的认识,也使得等值研究的结论更加合理、全面、可靠。
[1]谢小庆.对15种测验等值方法的比较研究[J].心理学报,2000,32(2):217-223.
[2]谢小庆.谢小庆教育测量学论文集[M].北京:北京语言大学出版社,2012:160.
[3]焦丽亚.基于IRT的共同题非等组设计中五种项目参数等值方法的比较研究[J].考试研究,2009(2):85-99.
[4]刘玥,刘红云.不同铆测验设计下多维IRT等值方法的比较[J].心理学报,2013,45(4):466-480.
[5]YAO L H.Multidimensional linking for domain scores and overall scores for nonequivalent groups[J].Applied Psychological Measurement,2011,35(1):48-66.
[6]张泉慧,黄慧英.IRT理论不同模型下同时校准等值方法的跨样本研究[J].中国考试,2016(2):3-8.
[7]BROSSMAN B G,LEE W C.Observed score and true score equating procedures for multidimensional item response theory[J].Applied Psychological Measurement,2013,37(6):460-481.
[8]HARRIS D J,CROUSE J D.A study of criteria used in equating[J].Applied Measurement in Education,1993(6):195-240.
[9]罗照盛.经典测量理论等值的误差研究[J].心理科学,2000,23(4):494-501.
[10]戴海崎.等值误差理论与我国高考等值的误差控制[J].江西师范大学学报,1999,32(1):30-36.
[11]PARSHALL C G,HOUGHTON P D B,KROMREY J D.Equating Error and Statistical Bias in Small Sample Linear Equating[J].Journal of Educational Measurement,1995,32(1):37-54.
[12]HAN YI KIM.A comparation of smoothing methods for the common item nonequivalent groups design[D].Iowa,US:The University of Iowa,2014.
[13]刘玥,刘红云.多维数据IRT真分数等值和IRT观察分数等值研究[J].心理学探新,2015,35(1):56-61.
[14]焦丽亚,辛涛.基于CTT的锚测验非等组设计中四种等值方法的比较研究[J].心理发展与教育,2006(1):97-102.
[15]DORANS N J,HOLLAND P W,THAYER D T,TATENENI K.Population invariance of score linking:Theory and applications to advanced placement program examinations[M].Princeton,US:Educational Testing Service,2003.
[16]BROSSMAN B G,LEE W C.Observed score and true score equating procedures for multidimensional item response theory[J].Applied Psychological Measurement,2013,37(6):460-481.
[17]张军之.基于多维IRT的测验等值研究[D].南昌:江西师范大学,2016.
[18]KOLEN M J,BRENNAN R L.Test Equating,Scaling and Linking:Methods and Practices(2nded)[M].New York,US:Springer,2004.
[19]吴锐.含题组测验的IRT等值问题研究[D].南昌:江西师范大学,2007.

