闵可夫斯基时空的命运
冯晓华 张 耀 高 策
(山西大学科学技术史研究所,太原 030006)
闵可夫斯基时空的命运
冯晓华 张 耀 高 策
(山西大学科学技术史研究所,太原 030006)
闵可夫斯基在1908年的“空间和时间”演讲已经成为一个经典,闵可夫斯基时空也已经成为一种自然观,现代物理学没有闵可夫斯基时空是不可能的。但是,历史上对这样一个观念的接受是一件极其复杂的事,原因涉及固守传统、优先权问题、对时空本身的不认可以及闵可夫斯基的早逝等。不过,在朋友与支持者的努力下,最终时空与闵可夫斯基的名字紧紧相连。然而,闵可夫斯基是如何形成这一观念的,则可能永远不得而知。
闵可夫斯基 闵可夫斯基时空 四维时空 数学家 物理学家 反应
爱因斯坦在瑞士苏黎世大学读书时的数学老师、德国数学家闵可夫斯基(H. Minkowski, 1864~1909)在1907年11月的演讲“相对性原理”[1]中,运用了四维方法;在同年12月的演讲“动体电磁过程的基本方程”[2](附录)中,给出了时空术语与时空图;在1908年9月的演讲“空间与时间”[3]中,把时间与空间结合到一起形成了四维时空。
通过这三场有关相对论的演讲,闵可夫斯基逐步提出了他的时空构想。其中最后一场演讲是他的事业的第一个高峰,直到三个月后,他和朋友们仍然在相当兴奋地校对这篇讲稿,准备发表。正在此时,闵可夫斯基因病突然离世。[4]
对于闵可夫斯基的这些工作,爱因斯坦(A. Einstein, 1879~1955)一开始认为,他们只是对自己的狭义相对论(1905年6月,在《论动体的电动力学》[5]中提出,该论文当时并没有很快被物理学家理解,直到1910年才开始被接受[6])的四维形式的改写[7](爱因斯坦后来认识到这是一种误解,不过直到现在还有人经常会认为三维和四维的相对论表示只是对相对性现象的不同描述[8]),而且这种数学对于物理学家而言很陌生,于是他和奥匈帝国物理学家劳布(J. Laub, 1884~1962)很快就将这种四维时空形式又改回了三维形式[9];再加上后来,爱因斯坦相对论获得成功,至今很大一部分人认为是爱因斯坦的狭义相对论要求同样地对待空间和时间[10],他的思想决定性地影响了闵可夫斯基[11];闵可夫斯基只是第一个从中认识到时空需要统一[12],并发展了爱因斯坦相对论数学形式的人[13]。的确,闵可夫斯基在第一个“相对性原理”演讲之前的一个月,为了希尔伯特(D. Hilbert, 1862~1943)的研讨会,确实曾写信向爱因斯坦索要狭义相对论论文的复印件[14]。
与此相反,闵可夫斯基的助手德国物理学家、数学家玻恩(M. Born, 1882~1970)指出,闵可夫斯基生前曾表示,当他看到爱因斯坦在1905年论文中声称,相对于彼此移动的观察者,不同局部时间的等价性时,他相当震惊,因为他自己早已得出了相同结论,只是希望首先解决其中的数学结构而没有发表。[15]
还有第三种观点,法国南希大学和庞加莱LPHS-档案馆的沃尔特(S. Walter)认为,匀速运动中可观察时间的等价性观念早已被庞加莱(J. H. Poincaré, 1854~1912)提到,闵可夫斯基可能没有注意到庞加莱对于局部时间的定义,也有可能是闵可夫斯基想到了计时员的精确等价。[16]
这些不同观点涉及的是四维时空发现的优先权问题,曾一度被科学史家进行研究。加拿大康科迪亚大学科学学院的佩特科夫(V. Petkov)认为,虽然爱因斯坦和庞加莱曾指出所有惯性观察员的时间都一样,但是他们没有涉及空间。[8]以色列海法大学的温斯坦(G. Weinstein)认为,闵可夫斯基从来没有提出优先权的要求,总是将这一伟大发现完全归功于爱因斯坦。[13]
尽管闵可夫斯基生前并没来得及完成他的大胆计划,去世的时候,他的时空构想也没什么影响,甚至还有不认可的声音;尽管他的早逝不可避免地进一步弱化了人们对其时空构想的早期评价[17],尽管这种弱化的一些部分延续至今;但历史结果是,时空与闵可夫斯基的名字紧紧相连。这是如何实现的?为什么是闵可夫斯基?
1 闵可夫斯基之前的四维时空
四维时空是不是闵可夫斯基的独创?答案是否定的。闵可夫斯基之前,一些数学家、小说家、物理学家和哲学家都曾描述过四维时空。较早的是17世纪,英国物理学家牛顿(I. Newton, 1643~1727)与德国数学家莱布尼兹(G. W. Leibniz, 1646~1716)的微积分将一维时间与三维空间联系到一起。[18]18世纪,法国数学家达朗贝尔(J. R. D’Alembert, 1717~1783)、拉格朗日(J. L. Lagrange, 1736~1813)和哲学家狄德罗(D. Diderot, 1713~1784)也认同时间是第四维度。[19]19世纪,英国数学家兼科幻小说家欣顿(C. H. Hinton, 1853~1907)分别在其科幻小说《第四维是什么?》[20]和科学论文《四维空间》[21]中正式讨论了四维时空。其中欣顿掌握了我们现在所说的时空图,甚至通过观察立方体在时空中的运动正确描述了超立方体。[22]不过,上述这些都不是以数学理论的形式讨论四维时空。
1889~1894年,德国物理学家赫兹(H. R. Hertz, 1857~1894)通过假定物质点在欧几里得空间和绝对时间中移动,发展了一个新的力学公式。[10]相关著作《在新背景下提出的力学原理》[23]在其去世的当年出版。1895年,英国科幻小说家威尔斯(H. G. Wells, 1866~1946)在小说《时间机器》[24]中,使用了时间和空间组合的四维空间,不过他没有将时间看作类空间的第四维。[25]1901年,匈牙利籍德国哲学家巴拉圭(M. Palagyi, 1859~1924)出版了《空间和时间的新理论》[26],他非常含糊地将空间和时间结合成一个四维实体,命名为流动空间,并给出了时空图,介绍了运动粒子的世界线和时间轴之间的时间角。不过巴拉圭除了指出流动空间中一点的坐标可以表示为x+it,y+it,z+it外,没有给出任何数学方案。从他的书中可以发现,他的时空思想仍处在心理层面,对数学和物理是无能为力的。后来当他注意到闵可夫斯基时空演讲时,还一度声称对时空图的优先权。1902年,欣顿还试图在四维中几何化电荷和电流,该文发表在《华盛顿物理学会通报》上[27]。1904年,韦尔斯的《时间机器》有了德文翻译,哥廷根大学理论物理研究所的戈纳(H. Goenner)认为原则上闵可夫斯基可能读过它[22]。
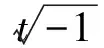
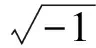
庞加莱不关心四维形式,甚至强烈拒绝四维形式,但是有人从他的文章中注意到了四维形式。首先是意大利墨西拿大学的数学物理学家马尔科隆戈(R. Marcolongo, 1862~1945),他是矢量分析的主要支持者,很快就从庞加莱的文章看出端倪,他用到了有一个虚轴的四维空间。之后就是闵可夫斯基1907~1908年间有关四维时空的三场演讲。[29]闵可夫斯基曾在1907年11月第一场演讲“相对性原理”中多次致谢庞加莱,尤其是庞加莱在1905年论文最后一节中提出的虚构时间坐标轴[30],闵可夫斯说自己的时空概念归功于庞加莱的这个研究。[6]
但是,在1908年的时空演讲中,闵可夫斯基只致谢了荷兰物理学家洛伦兹(H. A. Lorentz, 1853~1928)和爱因斯坦,没有提到庞加莱。对此,瑞典数学家米塔-列夫勒(G. Mittag-Leffler, 1846~1927)在1909年7月给庞加莱的信中,提到斯德哥尔摩数学家弗雷德霍姆(E. I. Fredholm, 1866~1927)认为,闵可夫斯基只是把庞加莱的思想做了不同的表达,庞加莱是首次以数学方式讨论过类似想法的人。庞加莱对这件事没有发表任何意见。不过在此前的几个月,即1909年4月哥廷根的新力学演讲中,庞加莱也没有提爱因斯坦和闵可夫斯基。1913年,德国物理学家索末菲(A. Sommerfeld, 1868~1951)重印闵可夫斯基的“时间与空间”时,在脚注中强调四维矢量思想之前被庞加莱提出过。沃尔特认为这不仅仅是简单的遗漏;因为闵可夫斯基的写作相当认真,且对庞加莱崇拜并熟悉他的电子动力学论文,对此,他也给出过两个推测。[17]
2 闵可夫斯基时空的逐步提出
庞加莱与马尔科隆戈都可以说是数学物理学家,研究这些问题并不出人意料;而闵可夫斯基在1907年之前的主要研究是纯数学,除了很少的例外,他发表的论文都与物理无关。[17]他为什么会在生命的最后几年专注于讨论时空以及相关的物理问题?并且,尽管闵可夫斯基在数学方面有很大成就,但还是他生命最后几年对时空的研究,才使他在科学界名声大噪。[32]
实际上,闵可夫斯基对理论物理的兴趣在他以一名数学家著称时就已存在。[32]这可以追溯到他在玻恩大学的时候(1885~1894)。在那里他接触到了很多物理学家,尤其密切接触过著名物理学家赫兹,写过一篇关于流体动力学的文章。之后闵可夫斯基去了苏黎世大学(1895),从与德国数学家希尔伯特的通信可知他对物理的兴趣仍旧热烈,尤其是热力学方面。1902年,闵可夫斯基加入哥廷根大学,在这里他深入参与了希尔伯特的所有科学活动,包括他的公理化物理学。[11]以色列特拉维夫大学科学史与科学哲学科恩研究所的科里(L. Corry)就认为,闵可夫斯基四维时空形式是对希尔伯特物理理论公理化的实现。[14]
当时哥廷根物理学家主要研究电子理论,尤其是德国物理学家亚伯拉罕(M. Abraham, 1875~1922)和考夫曼(W. Kaufmann, 1871~1947)还在电子动力学研究的最前沿。[6]于是闵可夫斯基配合希尔伯特组织了几场电动力学最新研究的研讨会。正是在这些研讨会上,闵可夫斯基逐渐渴望运用自己出色的数学能力解决物理学家无法解决的数学问题,来赶上当时物理研究的潮流。[11]他的时空新观点也是从这时开始发展的[6]。
其中,比较著名的一次是1905年夏天的电子理论高级研讨会,会上主要讨论庞加莱和洛伦兹的论文,目的是用成熟的数学分析扩展电动力学理论。德国物理学家劳厄(M. V. Laue, 1879~1960)、玻恩、亚伯拉罕以及索末菲出席了这次研讨会。据1955年玻恩的回忆,在这次研讨会上,闵可夫斯基提到了一些他自己还不是很明晰的四维方法。[7]
1907年11月,闵可夫斯基在哥廷根数学学会做了关于空间和时间的演讲“相对性原理”。这个演讲的起点是评论庞加莱1905年的工作。闵可夫斯基不满意庞加莱的方法,认为他仍旧没有解决引力与相对论的基本问题。不过,对于庞加莱论文最后一节用到但并不看好的四维矢量空间,闵可夫斯基却比较重视;[29]因为他意识到,把空间和时间统一成一个四维时空不只是一个方便的数学设计,只有在真实的四维世界里,相对性假设才有意义,[8]物理法则才能被完全理解[6]。这是闵可夫斯基与庞加莱不同的地方。闵可夫斯基本人很清楚这一点,他说这种形式化特征从来没被人注意到,甚至庞加莱[11]。这也是闵可夫斯基为什么会做一个主要思想已经被庞加莱在两年前发表(在三年前早已写好)的演讲的原因;甚至,这也是在时空问题上,我们为什么只歌颂闵可夫斯基而不说庞加莱的原因。[8]

不过,此次演讲中,闵可夫斯基的阐述更多的是一种方案,并不系统。[33]因为他当时还没有相应知识,所以出现在后来演讲中的一些关键概念,在此次演讲时仍为雏形。[16]
很快,一个月以后,闵可夫斯基将上述演讲提出的空间和时间新概念以及新的四维矢量方法用在了哥廷根科学学会的演讲“动体电磁过程的基本方程”中,该演讲1908年4月发表在《哥廷根新闻》(GottingerNachrichten)上。这是他去世前唯一发表的关于电动力学和相对论主题的论文。闵可夫斯基通过运用英国数学家凯莱(A. Cayley, 1821~1895)的矩阵演算将四维方法发展到了麦克斯韦-洛伦兹真空方程、移动介质的电动力学和洛伦兹协变力学中,构想了适合四维空间的力学基础。[17]在附录中,闵可夫斯基提出了他的标志性“时空”术语:时空点、时空丝、时空线、时空光锥以及时空图。[16]
这是一篇长而技术高超的论文,也是一篇无论数学形式还是物理结果都非常重要的论文[17]。通过这个工作,闵可夫斯基认为相对论变成了出众的数学研究领域,并且对于习惯考虑多维流形和接受非欧几何的数学家来说,在洛伦兹变换的应用中采用时间概念也不是很困难,所以他鼓励数学家用数学或者几何形式去研究相对性原理。[10]
1908年秋天,闵可夫斯基在哥廷根的几个场合都公开谈到了他的时空。1908年9月,在科隆举行的第80届德国科学家和医生学会年会上,闵可夫斯基首次有机会在哥廷根之外的学者面前谈他的时空。[17]此次他演讲的题目不再是物理味道的,而直接是“空间和时间”。对此,沃尔特认为,闵可夫斯基本人很可能意识到,之前自己将新的四维形式与一个争议性的主题“移动介质的电动力学”结合在一起,所以在紧接着的演讲中,简单地题为“空间与时间”,几乎完全是时空几何和力学要素,仅仅在电动力学方面示意了一下。沃尔特还认为能量守恒定律和经典牛顿力学定律之间的联系也直接影响到闵可夫斯基这次演讲的形成。[16]
“空间和时间”的主要结果都可以在闵可夫斯基的《动体电磁过程的基本方程》附录里找到[16],只是这次不再是附录,而是正文。此时,闵可夫斯基已经完全意识到时空能够使物理定律的统一性得到更优雅地描述[10],并且清晰理解了时空的这种重要性[4]。此次演讲的一个中心特征是时空图,全文共使用4次。对闵可夫斯基来说,时空图不仅仅是一个工具,而是表达自己引力定律的模型。[29]事实上时空图支撑起了闵可夫斯基的几何论证,强调了时空理论的数学本质,给出了四维矢量电流密度、电磁场的四维张量、四维条件下的麦克斯韦方程、四维速度矢量、四维力,这是狭义相对论四维理解的所有基本概念[32]。沃尔特认为闵可夫斯基还试图用时空图来区分他与爱因斯坦、洛伦兹对空间和时间的理解。[16]
在这次演讲中,闵可夫斯基再次强调了四维形式,他指出某些情况要求科学家放弃传统三维欧几里得空间的物理空间观,代之以某种二次型不变量所表征几何的真实四维时空世界。[34]在这样的世界中,不仅时间和空间的地位是平等的,而且一个惯性观察员的时间、空间与其他惯性观察员的时间、空间一样好,所以所有惯性观察员能够用他们自己的时间、空间来描述所有的物理现象。[8]闵可夫斯基还指出了四维时空与普通欧几里得空间的联系,他说,在新的时空观点下,三维几何变成了四维物理的一章。在同样精神的鼓舞下,他建议这种新的四维物理学应当有它自己的称号。[30]不过,闵可夫斯基没有将自己的工作描述为理论物理,也没把自己看作是理论物理学家。他向听众不断重申他是一个数学家[17],相对性原理是纯粹的数学[10]。事实上闵可夫斯基也是这样做的,在“时间与空间”演讲中,他回避了任何物理考虑,只通过纯数学论据引导出时空理论。沃尔特指出这是预防像爱因斯坦这样的物理学家对四维时空相对论的任何篡改。[16]
这是闵可夫斯基死前最后一次演讲,71位听众包括数学家、物理学家、天文学家、化学家、哲学家以及工程师。[4]科里认为,这肯定限制了闵可夫斯基对演讲主题和重点的选择。[11]比如在“相对性原理”中提到时空的非欧特征,在这里并没有出现;还有闵可夫斯基通过虚数定义时间坐标,保持了时空度量的欧氏特征。[10]这可能是他也意识到非欧几何会阻碍非数学家对时空形式的接受,毕竟,当时非欧几何在物理学中的应用还只是一种温和的倾向。[30]说到非欧特征,被四维几何深深吸引的美国艺术家和作家罗宾斯(T. Robbin, 1943~)认为,射影几何很可能对闵可夫斯基的时空思想有影响[18]。美国科学史家格里森(P. Galison, 1955~)也指出,闵可夫斯基因为有了阴影、投影和平面的视觉图象,所以从三维空间转换到新的四维空间。[6]
1908年圣诞节的前几天,闵可夫斯基将演讲稿“时间与空间”寄给《物理杂志》,1909年1月8日,《物理杂志》主编与闵可夫斯基还讨论了讲稿内容。[13]四天后,闵可夫斯基由于手术延误,阑尾破裂去世。[32]虽然闵可夫斯基英年早逝,但他那还没有什么名气的四维时空世界的梦想没有一同突然地被终止。[4]
3 朋友对其手稿与论文的出版与再版工作
闵可夫斯基去世一个月后,希尔伯特就在哥廷根科学院会议中回忆他最亲密的朋友兼同事闵可夫斯基的成就[35]。没有哪一个同事比希尔伯特更深受影响,他的纪念演讲反映了他深深的失落。同时,希尔伯特几乎是一个无私的人,他决心确保他的朋友对相对论的贡献不被遗忘。希尔伯特首先在闵可夫斯基的讣告中,迅速将“时间与空间”一同刊出来。他没做任何评论,完全同意闵可夫斯基的观点。[17]同年,这篇文章还刊载在《物理杂志》、《德国数学学会的年度报告》中。也在这一年,该文被莱比锡托伊布纳(B. G. Teubner)出版社以独立小册子形式出版,其中附有德国数学学会会长古兹曼(A. Gutzmer, 1860~1924)撰写的简要介绍[36]。他指出以独立小册子的形式出版是闵可夫斯基的最后遗愿,为了让更多的人能读到它。[4]到了年底,该文还有了意大利、法文版。
对于闵可夫斯基去世时留下的未发表的论文、未完成的手稿以及一大堆没有额外解释只有等式的相关笔记,希尔伯特委托一位年轻的瑞士数学家斯派泽(A. Speiser, 1885~1970)和闵可夫斯基去世前的助手玻恩进行筛选与整理[13]。1910年2月,玻恩在哥廷根大学数学学会讲解了闵可夫斯基未完成的电动力学内容。在这些讨论的基础上,玻恩重构了闵可夫斯基的想法[37],同年发表在《数学年刊》上。[11]
这一年,希尔伯特的学生德国数学家布卢门撒尔(L. O. Blumenthal, 1876~1944)与托伊布纳出版社合作出版一系列有关数学科学研究进展的专著。第一卷就是宣传闵可夫斯基对物理学的贡献,其中再版了闵可夫斯基的《动体电磁过程的基本方程》以及玻恩在闵可夫斯基笔记基础上整理的有关电子性质的研究。在前言中,布卢门撒尔指出,希望通过这个专题论文,激发更多不同学术背景的人研究闵可夫斯基的思想和相对论,促进和传播闵可夫斯基大胆梦想的理论,使下一代自觉意识到三维空间本身和一维时间本身已完全消退成阴影,只有二者的结合才具独立性,并且至今仍然生机勃勃。[38,4]
希尔伯特本人在1911年组织出版了《闵可夫斯基文集》[39]。希尔伯特与闵可夫斯基的终生友谊是科学史的一段佳话。两人对数学与物理的态度可谓志同道合,都相信数学和物理预先建立的和谐。闵可夫斯基早在1904年夏天微分方程讲座中就提到了这种不寻常的融合,并且在之后的演讲中也曾明确提到它。[7]在这个理念影响下,闵可夫斯基相信数学家可以从物理研究中获益,物理学家也可以从纯数学研究中获益,数学家和物理学家之间要有更好的合作。后面我们将会看到,要使纯数学家和物理学家信服这样的意见,还需要花些时间。[16]
另外,到了1913年,托伊布纳出版社曾出版的独立小册子《空间和时间》已经绝版。当索末菲得知这个情况后,他不是要求重新印刷,而是建议布卢门撒尔在他几乎流产的数学科学研究进展系列中出版第二卷。他的想法是以闵可夫斯基的“空间和时间”为中心,发表有关相对论论文的概要。在听取洛伦兹和爱因斯坦的建议后,这一卷以“相对性原理”[40]为题在当年发行。这是一本由索末菲评述的关于狭义相对论和广义相对论经典论文的论文集,包括洛伦兹1904年电子理论论文、爱因斯坦1905年的两篇相对论论文以及闵可夫斯基1907年和1908年的演讲。[4]该书后来被多次再版。两年后,索末菲又编辑、修改了闵可夫斯基生前与死后一直未发表的“相对性原理”。在他的协调下,该文首次在《物理年鉴》中刊载出来。
4 数学家对闵可夫斯基时空的反应
对于闵可夫斯基的时空,数学家最初的反应几乎是平静的,因为绝大多数数学家对物理没有兴趣。但是对希尔伯特而言,闵可夫斯基在理论物理的工作代表了未来的潮流。1908年5月,即《动体电磁过程的基本方程》发表的一个月后,希尔伯特就极力向德国数学家克莱因(F. C. Klein, 1849~1925)推荐闵可夫斯基。在他的争取下,闵可夫斯基很快成为了《数学年刊》编委会的一员。[16]
闵可夫斯基去世的几个月后,即1909年4月,克莱因说,“相对性原理”中洛伦兹群背后的思想实际上已经被他在1872年爱尔兰根纲领中预先考虑过。直到1917年,克莱因在讲 19世纪数学史时,仍然说闵可夫斯基论文中他最喜欢“相对性原理”。闵可夫斯基在自己所有论文中都没有提到克莱因的想法。沃尔特好奇,如果闵可夫斯基活着,他会对克莱因的评价作何反应呢。闵可夫斯基无法回应,沃尔特做了考查。他说尽管克莱因提出的爱尔兰根纲领和闵可夫斯基的相对论群理论之间的联系回想起来似乎清晰可见,但是当时爱尔兰根纲领的实际历史影响有时要比认为的小,没有直接证据表明闵可夫斯基在阐述自己关于时空的思想时是在思考爱尔兰根纲领。另外,庞加莱在群论与电动力学方程的洛伦兹协变之间建立明确联系后,几何体可以由它们的运动群表示是被广泛接受的一种概念,当然是闵可夫斯基最基本数学概念的一部分。[30]
对于闵可夫斯基前后几场演讲在术语使用上的变化,克莱因表达了自己的遗憾。在他看来,闵可夫斯基在相对论中隐藏了“最深处的、数学的、特别的不变理论思想”。1907年11月演讲中,闵可夫斯基提出时间与空间是一个四维非欧流形,这就要求给出四维矢量在非欧几何中的微积分。但是尽管伪超球面和双叶双曲面被认为是非欧空间的模型,可它们都没有构成四维流形。沃尔特认为,闵可夫斯基肯定意识到了这一点,之后他再也没有提及四维非欧流形。[30]
短短几年的工夫,一些数学家就理解了闵可夫斯基四维时空的概念。他们将它归入传统非欧几何研究的范围。如比利时数学家曼生(P. Mansion, 1844~1919),曾写过60多篇有关非欧几何的论文,在评论闵可夫斯基时空演讲时,认为闵可夫斯基自觉或不自觉地将非欧几何运用于物理。另外他和英国数学家马修斯(G. B. Mathews, 1861~1922)都赞同相对论是由几何学家研究和发展的观点。[30]克罗地亚萨格勒布大学数学教授瓦里查克(V. Varicak, 1865~1942),致力于从非欧几何的观点来研究相对论[41]。他以一个实四维坐标系为基础,在双曲几何中给出了闵可夫斯基的速度矢量关系,并在1911年德国数学年会与德国学会联合会上报告了这些研究。[30]在当时四维方法仍被忽视的情况下,他的方法获得了一定的关注。[29]
同时,闵可夫斯基的“相对性原理就是数学”的观点也被全世界数学系接收到。许多研究相对论的数学家相信相对论就是数学,因为他们早已熟悉闵可夫斯基理论中所采用的矩阵演算、双曲几何、群论的概念和技术。再加上英国数学家贝特曼(H. Bateman, 1882~1946)1911年在一篇文章[42]中将相对性原理看作是几何、偏微分方程、广义矢量分析、连续变换群、微分和积分不变量等各个数学分支的统一。于是,从全职数学教授到数学研究生,都响应号召开始研究和发展相对论。[17]
但并不是所有相对论数学家都认可闵可夫斯基的四维时空物理。1911年英国数学家坎宁安(E. Cunningham, 1881~1977)仍旧表示了对洛伦兹方法在研究动体电动力学时的偏爱。一年后,庞加莱也表达了同样的态度。[30]代数几何领军人物、意大利数学学会主席、罗马大学数学教授卡斯德尔诺沃(G. Castelnuovo)虽然在1911年的一篇文章[43]中承认闵可夫斯基几何方法的说服力,但他坚持认为是爱因斯坦修改了经典的空间概念,将相对论的时空归功于爱因斯坦。[17]
5 物理学家对闵可夫斯基时空的反应
尽管闵可夫斯基已经考虑到物理学家的接受性,在后来的演讲中回避了对非欧几何的引用,但是并不能保护它们免遭批评。物理学家最初对闵可夫斯基时空理论是激烈批判的。对于闵可夫斯基的《动体电磁过程的基本方程》,沃尔特认为有两点受到批判:一是新的四维形式,物理学家不熟悉其中四维空间结构和四维矢量符号所采用的非欧几何,他们普遍认为难以理解;二是以此为基础的移动介质电动力学,这一新的电动力学本身被认为与观测结果不一致。对于闵可夫斯基的四维形式以及新的电动力学,物理学家要么用一个熟知形式代替四维形式来改写相关方程,要么仅提供这种四维形式的大意。[16]
闵可夫斯基的《动体电磁过程的基本方程》在1908年4月5日发表不久,爱因斯坦就抱怨说,闵可夫斯基改写他的理论不过是多余的博学,自此数学扑向了相对论,他从此不再了解他自己了[33]。不只是抱怨,当月月底,爱因斯坦和他的合作者劳布迅速在一篇投稿中用普通三维矢量改写了闵可夫斯基的四维形式。文中给出的原因是,四维形式对读者提出了相当高的数学要求,尤其是其中的矩阵演算。[13]对于这种改写,人们可能认为会影响到闵可夫斯基的时空理论,不过事实不是这样的,因为在几个月之后的“空间和时间”中,闵可夫斯基为了预防对四维时空相对论的篡改,回避了任何物理考虑,只通过纯数学论据引导出他的时空理论。这引起了物理学家对数学的集中关注。[16]
同年,闵可夫斯基生前在哥廷根的同事、物理学家亚伯拉罕也用普通矢量改写了闵可夫斯基的理论[44]后,将其列入自己的辐射电磁波理论教材中。[16]的确,和闵可夫斯基的矩阵演算相比,采用普通矢量分析会让年轻物理理论家感到更多的自信。一个例子是德国物理学家维恩(W. Wien, 1864~1928)的表弟、物理学家马克思·维恩(M. Wien, 1866~1938)在1909年2月16日私下和索末菲说:读闵可夫斯基的文章让他晕头转向,时间和空间似乎混乱地聚集在一起。[30]
1909年春天,德国理论物理领军性人物普朗克(M. Planck, 1858~1947)在哥伦比亚大学的讲座中,称赞爱因斯坦与劳布对闵可夫斯基时空相对论的改写,称非欧几何是小孩子玩的,[45,30]尽管他也承认闵可夫斯基将爱因斯坦的理论放置在一个非常优美的数学形式中。维恩也持类似观点[46]。他们的评价主导了对闵可夫斯基时空理论的物理意见。沃尔特认为,虽然闵可夫斯基在“时间与空间”的演讲中,试图将自己的工作区别于爱因斯坦的工作,但这种努力至少对物理学家来说是失败了。[17]
但是,通过对闵可夫斯基论文的再版与翻译以及玻恩与其他几位物理学家对时空形式的采用[30],闵可夫斯基的时空得到了一定的传播,一些物理学家开始表达了对闵可夫斯基四维时空形式的欣赏。1909年,维恩通过考查非欧几何开始了对相对论的研究,尽管还是认为实验物理学开创了新的时空观,但他承认自己被闵可夫斯基理论的内在美和一致性所吸引。[47]还有一个有趣的例子可以归到这里,前面谈到爱因斯坦和他的合作者劳布对闵可夫斯基的四维时空没什么好印象,自然地,劳布也想知道其他物理学家对闵可夫斯基方法的看法。于是他询问德国理论物理学家康托(M. Cantor, 1861~1916)如何看待闵可夫斯基理论中把时间看作第四空间坐标的真实物理意义。劳布没有得到答案,但他认为康托本人对其中的非欧几何留下了深刻印象。[30]
捍卫闵可夫斯基时空理论的关键人物是希尔伯特的学生、克莱因的得意门生索末菲[17],他起初对爱因斯坦的理论持怀疑态度,后来发现闵可夫斯基的时空理论非常有说服力,尤其是爱因斯坦的“某些奇怪”结果从闵可夫斯基的时空观点来看就变得非常清楚,而且它在问题解决中还具有实践优势。随着闵可夫斯基的去世,索末菲成了物理领域中最具影响力的时空理论拥护者。在1909年9月萨尔茨堡举办的德国自然科学家和医生学会会议上,索末菲就试图激起物理学家对闵可夫斯基时空的兴趣。他说,闵可夫斯基深刻的时空观不仅系统地促进了相对论的全面构建,而且在具体问题中作为简明的指南也很成功。[30]
一年后,通过索末菲、亚伯拉罕和美国物理化学家刘易斯(G. N. Lewis, 1875~1946)的努力,闵可夫斯基的矩阵演算转化成了一个便捷的四维矢量分析,最终进入张量计算[48-51]。这些矢量和张量对闵可夫斯基微积分的改写以及像索末菲和亚伯拉罕这样受人尊重的理论家的倡导,毫无疑问鼓励了其他物理学家对时空形式的尝试,而他们也确实认识到,与普通矢量分析或直角坐标法相比,时空形式具有非常明显的优势。[30]这之后,相当一部分物理学家开始研究相对论[29],就连普朗克的态度也发生了改变。1910年9月,在德国学会的致辞中,他致谢了数学家,因为与相对性原理有关的大部分抽象问题是由数学家做出的。他还指出相对论的标准数学方法与四维几何的发展是完全一样的。[30]
在德国矢量电动力学令人兴奋的氛围下,年轻理论物理学家开始热切地阅读索末菲的工作。当时的维也纳物理学家弗兰克(P. Frank, 1884~1966)颇有些感慨地说,对于古怪的符号系统与术语,物理学家已经超负荷了,还是索末菲的系统好啊。确实在1910~1911年,物理学家被湮没在令人困惑的一大批新的符号系统中,包括普通矢量代数、四元微积分、双曲坐标系以及三个四维形式,而索末菲等人都相信矢量符号在物理与几何中的有效性,所以他们通过矢量符号来统一各种作者使用的多种符号。[29]
劳厄在1911年出版的相对论教科书[52]对时空形式的传播起了重要作用。它系统而优雅地把索末菲的四维向量代数扩展到相对论中[30]。该书在规范四维代数的术语和符号方面很知名[29]。不过,爱因斯坦仍旧表示,劳厄的教科书很难理解[33]。同年,在卡尔斯鲁厄举办的德国数学年会与德国学会联合会上,普朗克指出相对论不能再视为当前的一个研究对象,它已经成为物理学的一部分。当年德国顶尖物理期刊《物理年鉴》的一个明显特点就是四维矢量运算,在9篇关于相对论的文章中有8篇采用了时空形式。年底,时空形式就已经取代普通矢量成为研究相对论的首选工具。[30]
1912年,时空形式已经赢得了物理学家的信心,成为相对论前沿研究的标准。而且同年11月,美国科学家吉布斯(J. W. Gibbs, 1839~1903)的最后一位博士生、麻省理工数学家威尔逊(E. B. Wilson, 1879~1964)和他的同事刘易斯,在《相对论的时空流形:力学和电磁学的非欧几何》[53]中,把时空的非欧几何属性光明正大地说了出来,这曾是闵可夫斯基出于物理学家的接受性而回避的。[30]这一年,爱因斯坦也开始后悔了,他对数学的态度开始发生重大转变。[13]主要原因是,过去一段时间,当他越是研究广义相对论,越是不得不承认闵可夫斯基方法的内在价值;最终,他充分意识到,闵可夫斯基时空的不变线元ds2=dx2+dy2+dz2-(cdt)2在取无穷小时就是表示广义相对论弯曲时空以及建立时空结构与引力势关系的基础。[33]
闵可夫斯基时空理念的首次重要阐述在1916年由爱因斯坦完成[54]。他成功地将重力与时空弯曲联系起来,表明广义相对论就是一种宏观的时空理论。[32]这个曾经对他的数学老师有复杂感情的学生,此次终于认可了老师的工作。他在论文中说,狭义相对论的推广在相当大程度上是由闵可夫斯基促进的,数学家闵可夫斯基第一个清晰地认出时间和空间的形式对等,并使用它来进行理论构建。[4]的确,没有时空概念广义相对论是不可能的[8]。最终,包括爱因斯坦在内的很多物理学家彻底认可了闵可夫斯基时空几何方法对相对论的促进。[16]
不过此时,物理学家仍然怀疑非欧几何会在物理中起重要作用。对此,沃尔特总结了三个原因:首先是从一开始索末菲就强烈反对。其次是没有现成的非欧几何风格的矢量演算供物理学家使用。尽管有少数人能拿到威尔逊和刘易斯非欧几何风格向量代数的复印件,但是在运用之前首先得死记硬背大量的符号约定,而且,改写普通向量代数用于双曲空间仍然是不可行的,瓦里查克本人在1924年也不得不承认这一点。再次,或许是当时非欧几何风格只算是一个物理尝试,还无法吸引物理学家采用它。[30]
另外,尽管在1912年,即爱因斯坦后悔没重视数学的那一年,庞加莱也承认四维闵可夫斯基时空物理定律取代洛伦兹-庞加莱电子理论得到了广泛接受,[55,17]但他仍然喜欢采用后者,因为它不需要空间概念的改变。庞加莱在这一年去世了,但是十多年后,庞加莱的绝大多数法国同事们还在继承庞加莱的习惯,使用笛卡尔直角坐标表示普通矢量,这是法国对待德国矢量符号运动的典型态度。[29]
6 结 语
正如庞加莱预测的,在物理中运用四维语言障碍重重,这种语言的构建的确耗费了闵可夫斯基相当的艰辛和努力。[29]首先是看待数学在物理中所起作用的问题上,闵可夫斯基的观点不仅与物理学家而且与德国大学里那些无视物理的数学家都截然不同,这使得对闵可夫斯基时空的接受成为一件复杂的事。[16]其次,即使闵可夫斯基尽力说服数学家,他的工作是独立的,但大部分德国物理学家认为时空理论就是爱因斯坦理论的纯形式发展。[17]
遗憾的是,闵可夫斯基在自己的一生中并没有改变这种状况。幸运的是,他的朋友和支持者立即追随他的观点,带领时空物理进入相对论的舞台,[4]使时空流形以及四维矢量语言成为与洛伦兹、庞加莱和爱因斯坦基本思想密不可分的部分。[11]
20世纪初,数学在构建物理理论中的作用作为一种新的认识影响了一大批数学家,如法国的嘉当(É. J. Cartan, 1869~1951)、意大利的列维-奇维塔(T. Levi-Civita, 1873~1941)、美国艾森哈特(L. P. Eisenhart, 1876~1965)、荷兰的斯考滕(J. A. Schouten, 1883~1971)和德国的外尔(H. Weyl, 1885~1955)。他们纷纷转向理论物理寻找新的研究方向,来重新征服被理论物理学家占据的领域。[17]
之后,随着爱因斯坦相对论成为物理学中的一场革命,对闵可夫斯基的认可又开始弱化。希尔伯特在一封为理论物理学家客座讲师申请资金支持的信中,承认爱因斯坦的贡献比闵可夫斯基的更基础。[17]外尔在1947年写给闵可夫斯基姐姐范妮(Fanny Minkowski, 1863~1954) 的信中说,人们在自己专业以外的学科有所贡献,往往会对他所掌握的其他学科的东西自豪,再加上缺乏大局观,很容易倾向于夸大地评价自己的贡献。演讲“时间与空间”就是这样,闵可夫斯基想让一个物理的过渡阶段成为不朽。[11]
但是,不可否认闵可夫斯基时空在物理思想自身里是全新的[16],它不仅仅是物理中的一个有用工具,而是一种新的自然观,它点燃了很多科学家的想象。在过去的100多年里,这个观点被用于从电磁场到黑洞的物理领域中[6],对20世纪物理学产生了巨大的影响,现代物理学没有闵可夫斯基时空是不可能的[8]。如今,闵可夫斯基的“空间和时间”演讲已然成为一个经典[4], 闵可夫斯基时空对于理论物理的数学意义已经达成一致共识。但是100多年来,对于闵可夫斯基时空本身的性质一直没有达成共识[8]。 一方面,闵可夫斯基时空是爱因斯坦引进度规场后才完整建立的,只有在场论的构架下讨论才有意义。另一方面,20世纪物理学两大支柱量子力学和广义相对论结合后建立的量子重力(或量子引力)理论的两种不同进路形成了对闵可夫斯基时空的不同态度:继续保持或者变革和修正。所以,闵可夫斯基时空概念到底是一大进步还是约束和限制了物理学家在量子化重力过程中的想象力,仍是个重要问题。*这是引用审稿专家的意见。
致 谢 感谢审稿专家专业和细致的修改意见,使得文章的质量得到了极大提升,尤其是文章一开始问题引出部分,变得更加清晰,文章的最后一句话,变得更加明确。
1 Minkowski H.Das Relativitätsprinzip[J].AnnalenderPhysik, 1915, 352(15): 927~938.
2 Minkowski H. Die Grundgleichungen für die Elektromagnetischen Vorgänge in bewegten Körpern[J].Nachr.Ges.Wiss.Göttingen, 1908: 53~111.
3 Minkowski H. Raum und Zeit[J].PhysikalischeZeitschrift, 1909, 10: 104~111.
4 Rowe D E. A Look Back at Hermann Minkowski’s Cologne Lecture “Raum und Zeit”[J].TheMathematicalIntelligencer, 2009, 31(2): 27~39.
5 Einstein A. Zur Elektrodynamik bewegter Körper[J].AnnalenderPhysik, 1905, 322(10): 891~921.
6 Galison P. Minkowski’s Space - Time: From Visual Thinking to the Absolute World[J].HistoricalStudiesinthePhysicalSciences, 1979, 10: 85~121.
7 Pyenson L. Physics in the Shadow of Mathematics: the Göttingen Electron - Theory Seminar of 1905[J].ArchiveforHistoryofExactSciences, 1979, 21(1): 55~89.
8 Petkov V.MinkowskiSpacetime:AHundredYearsLater[M]. Dordrecht, Heidelberg, London, New York: Springer, 2010. Preface.
9 Einstein A, Laub J. Über die Elektromagnetischen Grundgleichungen für bewegte Körper[J].AnnalenderPhysik, 1908, 331(8): 532~540.
10 Bertolami O. The Adventures of Space - Time[M]// Petkov V (Ed.).RelativityandtheDimensionalityoftheWorld. Netherlands: Springer, 2007.31~47.
11 Corry L. Hermann Minkowski and the Postulate of Relativity[J].ArchiveforHistoryofExactSciences, 1997, 51(4): 273~314.
12 Dieudonné J. Hermann Minkowski[M]// Gillispie C C.DictionaryofScientificBiography. New York: Scribner’s Sons, 1981.411~414.
13 Weinstein G. Max Born, Albert Einstein and Hermann Minkowski’s Space - Time Formalism of Special Relativity[DB/OL]. (arXiv preprint arXiv:1210.6929, 2012)[2015- 12- 05].https://arxiv.org/ftp/arxiv/papers/1210/1210.6929.pdf.
14 Corry L. Hermann Minkowski, Relativity and the Axiomatic Approach to Physics[M]// Petkov V.MinkowskiSpacetime:AHundredYearsLater. Dordrecht, Heidelberg, London, New York: Springer, 2010.3~42.
15 Born M.MyLife:RecollectionsofaNobelLaureate[M]. New York: Scribner’s Sons, 1978.131.
16 Walter S. Hermann Minkowski’s Approach to Physics[J].MathematischeSemesterberichte, 2008, 55(2): 213~235.
17 Walter S. Minkowski, Mathematicians, and the Mathematical Theory of Relativity[J].TheExpandingWorldsofGeneralRelativity, 1999, 7: 45~86.
18 Robbin T.ShadowsofReality:theFourthDimensioninRelativity,Cubism,andModernThought[M]. New Haven, London: Yale University Press, 2006.44~49.
19 Archibald R C. Time as a Fourth Dimension[J].BulletinoftheAmericanMathematicalSociety, 1920, 20(8): 409~412.
20 Hinton C H. What is the Fourth Dimension[J].ScientificRomances, 1884, 1: 1~22.
21 S. Four - Dimensional Space[J].Nature, 1885, 31(804): 481.
22 Goenner H. On the History of Geometrization of Space - Time: From Minkowski to Finsler Geometry[DB/OL]. (arXiv preprint arXiv:0811.4529, 2008)[2015- 12- 25]. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.245.2310&rep=rep1&type=pdf.
23 Hertz H.DiePrinzipienderMechanikinNeuemZusammenhangeDargestellt[M]. Leipzig: Johann Ambrosius Barth, 1894.
24 Wells H G.TheTimeMachine[M]. London: William Heinemann, 1895.
25 Bork A M. The Fourth Dimension in Nineteenth - Century Physics[J].Isis, 1964, 55(3): 326~338.
26 Palagyi M.NeueTheoriedesRaumesundderZeit[M]. Leipzig: Engelmann, 1901.
27 Hinton C H. The Recognition of the Fourth Dimension[J].BulletinofthePhysicalSocietyofWashington, 1902, 14: 179~203.
28 Poincaré H. Sur la Dynamique de l’électron[J].ComptesRendusdel’AcademiedesSciences, 1905, 140: 1504~1508.
29 Walter S. Breaking in the 4 - Vectors: the Four - Dimensional Movement in Gravitation, 1905-1910[M]// Renn J (ed.).TheGenesisofGeneralRelativity. Netherlands: Springer, 2007.1118~1178.
30 Walter S. The Non-Euclidean Style of Minkowskian Relativity[M]// Gray J (ed.).TheSymbolicUniverse:GeometryandPhysics1890-1930. Oxford: Oxford University Press, 1999.91~127.
31 Poincaré H. La Relativité de l’espace[J].AnnéePsychologique, 1907, 13: 1~17.
32 Pyragas K, Svirskas K. On the Biography and the Scientific Heritage of Hermann Minkowski[J].BalticAstronomy, 2005, 14: 323~330.
33 Corry L. The Influence of David Hilbert and Hermann Minkowski on Einstein’s Views over the Interrelation between Physics and Mathematics[J].Endeavour, 1998, 22(3): 95~97.
34 Walter S. Minkowski’s Modern World [M]// Petkov V.MinkowskiSpacetime:AHundredYearsLater. Dordrecht, Heidelberg, London, New York: Springer, 2010.43~64.
35 Hilbert D. Hermann Minkowski[J].MathematischeAnnalen, 1910, 68: 445~471.
36 Damour T. What is Missing from Minkowski’s “Raum und Zeit” Lecture[J].AnnalenderPhysik, 2008, 17(9,10): 619~630.
37 Minkowski H.Eine Ableitung der Grundgleichungen fur die elektromagnetischen Vorgange in bewegten Korpern(Aus dem Nachlaß von Hermann Minkowski bearbeitet von Max Born in Gottingen) [J].MathematischeAnnalen, 1910, 68: 526~551.
38 Blumenthal O.ZweiAbhandlungenuberdieGrundgleichungenderElektrodynamik(MiteinemEinfuhrungswortvonOttoBlumenthal,FortschrittedermathematischenWissenschafteninMonographien,Heft1)[M]. Leipzig: Teubner, 1910.
39 Minkowski H. Gesammelte Abhandlungen[M]. 2 vols. ed. D. Hilbert. Leipzig: Teubner, 1911.
40 Blumenthal O.DasRelativitatsprinzip(EineSammlungvonAbhandlungen.MitAnmerkungenvonA.SommerfeldundVorwortvonO.Blumenthal,FortschrittedermathematischenWissenschafteninMonographien,Heft2)[M]. Leipzig: Teubner, 1913.
41 Varicak V. Anwendung der Lobatschefskijschen Geometrie in der Relativtheorie[J].PhysikalischeZeitschrift, 1910, 11: 93~96.
42 Bateman H. Mathematics and Physics at the British Association[J].Nature, 1911, 87(2189): 498~502.
43 Castelnuovo G. Il Principio di Relativita e Fenomeni Ottica[J].Scientia(RivistadiScienza), 1911, 9: 64~86.
44 Abraham M.ElektromagnetischeTheoriederStrahlung[M]. 2nd edn. Leipzig: Teubner, 1908.
45 Planck M.AchtVorlesungenuberTheoretischePhysik:GehaltenAnDerColumbiaUniversityInTheCityOfNewYorkImFrühjahr1909[M]. Leipzig: Hirzel, 1910.
46 Wien W.UberdieWandlungdesRaum-undZeitbegriffsinderPhysik[M]. Sitzungsberichte der physikalisch-medicinischen Gesellschaft zu Wurzburg, 1909.29~39.
47 Pyenson L. Relativity in late Wilhelmian Germany: The appeal to a preestablished harmony between mathematics and physics[J].ArchiveforHistoryofExactSciences, 1982, 27(2): 137~155.
48 Sommerfeld A. Zur Relativitätstheorie(I): Vierdimensionale Vektoralgebra[J].AnnalenderPhysik, 1910, 32: 749~776.
49 Sommerfeld A. Zur Relativitätstheorie(II): Vierdimensionale Vektoranalysis[J].AnnalenderPhysik, 1910, 33: 649~689.
50 Abraham M. Sull’elettrodinamica di Minkowski[J].RendicontidelCircoloMatematicodiPalermo, 1910, 30: 33~46.
51 Lewis G N. On Four - Dimensional Vector Analysis, and its Application in Electrical Theory[J].ProceedingsoftheAmericanAcademyofArtsandScience, 1910, 46: 165~181.
52 Laue M V.DasRelativitätsprinzip[M]. Braunschweig: Vieweg, 1911.
53 Wilson E B., Lewis G N. The Space - Time Manifold of Relativity. The non-euclidean geometry of mechanics and electromagnetics[J].ProceedingsoftheAmericanAcademyofArtsandSciences, 1912, 48(11): 389~507.
54 Einstein A. Die Grundlage der allgemeinen Relativitatstheorie[J].AnnalenderPhysik, 1916, 354(7): 769~822.
55 Poincaré H. L’Espace et le Temps[J].Scientia(RivistadiScienza), 1912, 12: 159~170.
The Fortune of Minkowski Space - time
FENG Xiaohua, ZHANG Yao, GAO Ce
(InstitutefortheHistoryofScienceandTechnology,ShanxiUniversity,Taiyuan030006,China)
Minkowski’s speech “Space and Time” in 1908 has become a classic, and Minkowski space - time also has become a conception of nature. Now, modern physics without Minkowski space - time is impossible. However, the history of the acceptance of the concept was an extremely complex matter, due to reasons such as conservatism, priority problems, disagreements over the fundamental nature of space - time, and Minkowski’s untimely death, etc. In the end, thanks to the efforts of friends and supporters, space - time and the name of Minkowski became closely linked. Yet, how the idea came to Minkowski may never be known.
Minkowski, Minkowski space - time, four - dimensional space - time, reaction of mathematicians, reaction of physicists
2016- 06- 14;
2016- 10- 08
冯晓华,女,1977年生,山西原平人,讲师,主要研究方向为数学史;张耀,1990年生,山西霍州人,科学技术史在读研究生;高策,1958年生,山西太原人,教授,主要研究方向为科技史。
教育部人文社科重点研究基地重大项目“数学、物理学的关系与科学理论的语境模型研究”(项目编号:13JJD720012);教育部重点研究基地重大项目“语境论数学哲学的基本问题研究”(项目编号:12JJD720012)。
N091∶K816.1
A
1000- 0224(2017)01- 0098- 14

