《符天历》历元问题再研究

钮卫星

(上海交通大学科学史与科学文化研究院,上海 200240)

《符天历》历元问题再研究

钮卫星

(上海交通大学科学史与科学文化研究院,上海 200240)

文章通过考察相关研究和文献资料,提出《符天历》历元的确切日期为显庆五年庚申岁正月壬寅雨水合朔,该雨水为定气而不是一般认为的平气,对应公元日期为660年2月16日,对应的儒略日序为1962169；解决了历来部分学者以为的《符天历》历元“气朔不合”与文献记载《符天历》历元“气朔相合”之间的矛盾；并引用了几则与《符天历》有关的传世星占文献和出土历日资料中的积日数据对结论加以讨论和验证；最后通过对《九执历》积日算法的讨论,指出使用该算法不能支持《符天历》历元为显庆五年正月三日雨水甲辰(660年2月18日)的结论。

《符天历》 历元 积日 定气

1 前人工作回顾和问题的提出

《符天历》为活动于唐建中至元和年间(780～820 )的术士曹士蒍所撰。据《新五代史·司天考》记载：“唐建中时,术者曹士蒍始变古法,以显庆五年为上元,雨水为岁首,号《符天历》。然世谓之小历,只行于民间。”([1],670页)然而《符天历》与域外传入的星命术一起配合使用,逐渐产生了影响,得到当时一些历法家的重视,如五代时历法家马重绩以《符天历》为法,改名《调元历》,获得官方正式颁行。([1],670页)日本僧人日延于公元953年在吴越国司天台学习了《符天历》,并将其传入日本([2],118～119页)。《符天历》在日本与唐《宣明历》长期相参使用,因此它对日本历法也产生了较大影响。

《符天历》使用近距历元、以雨水为岁首等具有明显域外天文历法特征的做法得到了一些研究的确认[3],然而针对《符天历》历元的具体日期,历法史研究者们尚未达成一致意见。薮内清指出《符天历》历元所在年份显庆五年的雨水为正月三日甲辰(660年2月18日),与该年正月朔(660年2月16日)相差两天。在考察《续群书类从》卷908中一则日本天永三年十二月二十五日《宿曜运命勘录》所载积日数时(详见下文讨论),薮内清发现若从显庆五年“雨水甲辰”算起,积日数差了两日。他无法解释这两天差异,因此提出《符天历》的积日可能是从显庆五年正月朔算起。也就是说,薮内清认为《符天历》历元气朔是不相合的,历元是正月朔,并提出雨水为“岁首”的记载是“误记”,应为“气首”。([4],83～94页)

陈久金则认为“既称以雨水为岁首,就必然是气朔相合”,但也承认“如果以精密数值推算,显庆五年正月气朔确实相距两天”。他推测气朔之间两天的差异可能是《符天历》使用了不精确的回归年长度而导致的。[5]

孔庆典提出《符天历》的积日计算使用了《九执历》所载的算法,并运用该算法计算出天永三年《宿曜运命勘录》中的积日起点恰好显庆五年“正月三日雨水甲辰”,所以“《符天历》的历首确始于显庆五年雨水,而非目前学界普遍认为的显庆五年正月朔”。([6],162～163页)

那么,《符天历》历元究竟是显庆五年正月壬寅朔,还是雨水甲辰？气朔之间到底是存在两天的差异,还是“气朔相合”的？该历元的确切日期是哪一天？笔者拟在本文通过考察相关研究和文献资料,解决《符天历》历元“气朔不合”的矛盾,提出《符天历》历元的确切日期,并引用几则与《符天历》有关的星占文献中的积日资料加以讨论和验证。

2 《符天历》历元的确切日期

陈垣《二十史朔闰表》给出显庆五年正月朔的日干支为壬寅,对应公元日期为660年2月16日[7],以往的研究对此均无异议。笔者在此援引两则文献记录加以证实：其一,《册府元龟》卷3载有一通抄写古典时无须避唐高宗李治名讳的诏书,颁发于“显庆五年正月壬寅”[8]；其二,《唐文续拾》卷14“樊宏度墓志铭”中记载有“显庆五年岁次庚申二月壬申朔十三日甲申合葬”一事[9]。壬申距壬寅30天,据此可断定显庆五年正月大、壬寅朔。

薮内清认为显庆五年雨水为正月三日甲辰——这一点也得到其他研究者的认同,但未能给出该说法的依据([4],83～94页)。笔者编制程序调用数字行星历表DE404[10]算得显庆四年冬至时刻归算为西安地方时后为659年12月19日癸卯6时2分,加上4个平气的天数(约60.874天),得660年2月18日甲辰3时1分(西安地方时)。这就是显庆五年平气雨水所交时刻。因此,笔者推断薮内清等人所指的“显庆五年正月三日甲辰雨水”是一种平气。

在清代《时宪历》以前,中国古代官方历法确实一直使用平气注历,然而各种证据表明被称作“民间小历”的《符天历》却是使用定气注历的。《七曜攘灾决》被薮内清推断为属于《符天历》系统([4],83～94页),在其第2卷中专门收录了一份“黄道日躔定气”表格,并强调“太阳之精凡行背以定气为准”。[11]日本《续群书类从》卷908保存的一则《宿曜运命勘录》*薮内清在《关于唐曹士蔿的符天历》([4],88页)一文中摘录了《续群书类从》卷908保存的这则《宿曜运命勘录》的开头部分,并对有关星占内容进行了讨论。,是使用《符天历》进行推算的(详见下文讨论),其开头为：“天永三年壬辰十二月廿五日戊申时丑诞生男,大寒初日,算勘：自上元庚申岁距今日所积日数十六万五千四百廿八日。”[12]此处“天永三年壬辰十二月廿五日戊申”为1113年1月14日,可算得该日太阳黄经为300.59度,虽然有半日误差,但基本符合大寒定气的定义。又东京大学“东京都六条有康氏所藏文书”中有一则《宿曜御运录》*桃裕行在《关于〈符天历〉》”([2],118页)一文中提到了《续群书类从》所保存的《宿曜运命勘录》和6条有康氏藏《宿曜御运录》,并讨论了其中所用历法的历元。感谢杨凯为本文作者把该文从日文翻译成中文。,也是一则使用《符天历》推算的星命书(详见下文讨论),其开头为：“文永五*原文“五”误作“六”。日本文永六年为公元1269年,年干支为己巳,故可知戊辰年当为文永五年。年戊辰六月己未廿六日丙午时亥御诞生男,当立秋七日,算勘：积日廿二万二千二百四十五日。”[13]“文永五年戊辰六月己未廿六日丙午”即1268年8月6日,该年立秋(定气)初日在7月31日,因此8月6日正好“当立秋七日”。

以上三个例证表明《符天历》是使用定气注历的。近代以来在日本天理图书馆收藏的《天文秘书》中发现的《符天历》残篇《符天历经日躔差立成》抄本则进一步证明《符天历》是有办法推算定气的。《符天历经日躔差立成》开篇写道：

日躔差法,经文幽微,非久习者,致或难了固。今新张立成,得其意,定率即固。经朔、弦、望、中日度分,以差积度分,盈加缩减,为定日度分。其后每日累加一度。若盈缩历一度已上九十一度已下,以差率盈加缩减；九十二度已上百八十二度已下者,以差率盈减缩加。次日定度分,去命度数,加常定法。专与经意不相违之。[14]

以上文字类似于一种对所给出的数表所作的使用说明,在该残篇接着给出的数表中提供了从平太阳位置求得真太阳位置的方法。中山茂利用该数表拟合出《符天历》求太阳真位置与平位置差的近似公式：

式中l是太阳平黄经,λ是太阳真黄经。利用《符天历》残篇提供的数表或上述近似公式,可以求得太阳的真实位置,并可进一步确定各定气的日期。

因此,笔者推断被《符天历》选作历元的显庆五年雨水应是定气。据DE404[10]可算得660年2月16日壬寅西安地方时14时17分太阳黄经为330.00度,此即为雨水定气时刻；显庆五年正月合朔时刻为同日西安地方时21时41分,日月俱在黄经330.31度。可见,显庆五年正月朔与雨水定气是在同一天内,是“气朔相合”的。薮内清假定《符天历》历元气朔不相合、雨水晚正月朔二日([4],83～94页),是不必要的。

《符天历》以“雨水为岁首”的记载见于《新五代史》卷58《司天考》,是为了说明马重绩作《调元历》是对《符天历》同样做法的模仿。在《新五代史》卷57《杂传第四十五》的“马重绩传”中对此也有记述：“天福三年,重绩上言：……自前世诸历皆起天正十一月为岁首,用太古甲子为上元,积岁愈多,差阔愈甚。臣辄合二历,创为新法。以唐天宝十四载乙未为上元,雨水正月中气为气首。……乃下诏班行之,号《调元历》”([1],665页)这里马重绩强调了放弃传统的以“十一月甲子合朔冬至”为历元的做法,改为以雨水为历元。对此,可算得天宝十四载乙未正月辛酉合朔雨水(755年2月16日)。可见,从曹士蒍到马重绩,虽然选取不同的近距历元年份,但以“气朔相合”的正月合朔雨水作为历元的做法是一脉相承的。

至此,我们可以给出《符天历》历元的确切日期是显庆五年庚申岁正月壬寅雨水合朔,对应公元日期为660年2月16日,对应的儒略日序为1962169。

3 传世星命书、出土历日资料中的积日和《符天历》历元

明确了《符天历》以显庆五年正月壬寅雨水合朔(660年2月16日)为历元,从而就解决了薮内清在考察《续群书类从》卷908日本天永三年十二月二十五日《宿曜运命勘录》所载积日数时所遇到的2日差异的困难。《续群书类从》“宿曜运命勘录”给出其积日为“自上元庚申岁距今日所积日数十六万五千四百廿八日”,这里的上元庚申岁即《符天历》的历元年份显庆五年。“天永三年壬辰十二月廿五日戊申”可换算为公元1113年1月14日,儒略日序为2127595,与《符天历》历元相差165426日。古代星命书中的积日是指经过的所有日子(更多例证可参见下文有关案例的讨论),首尾两天都算上,所以积日的数目还要在两个儒略日序差值上加上1日,得165427。《续群书类丛》“宿曜运命勘录”所载的积日数为165428,比所算得日数多1日。这一日之差的原因,薮内清已经给出解释：由于日本平安朝时代以寅时为一日起算点,该件星命书所记的出生时辰丑时仍属于前一日戊申。([4],88页)如果以中国传统的夜半为一日起算点的话,该求卜者生于天永三年十二月二十六日丑时(1113年1月15日,儒略日序为2127596),到《符天历》历元的积日正好为165428。可见,《续群书类从》“宿曜运命勘录”所给出积日的起点是《符天历》历元显庆五年庚申岁正月壬寅雨水合朔。

另外,上文提及东京大学“东京都六条有康氏所藏文书”中有一则“宿曜御运录”,其中所载求卜者生辰为“文永五年戊辰六月己未廿六日丙午”,可换算成公元1268年8月6日,儒略日序为2184413,与《符天历》历元(1962169)之间,算上首尾,积日数为222245,与所载“积日廿二万二千二百四十五日”相符。由此可以肯定六条有康氏所藏文书“宿曜御运录”也是以《符天历》为基础进行推算的。

又,俄藏黑水城汉文文献中有一份“X37刻本绍圣元年历书”残篇,其中注有“积日一十五万八千四百九十二日”的字样。绍圣元年正月初一为公元1094年1月19日,对应儒略日序为2120660,与《符天历》历元显庆五年正月一日(1962169)之间算上首尾,积日数正好为158492。可见该份“X37刻本绍圣元年历书”残篇上所注积日的历元也是显庆五年正月合朔雨水,该份历书与《符天历》之间有密切的关系。

以上所讨论的两则传世星命书文献和一则出土历日资料中的积日数据都是从《符天历》的历元显庆五年正月合朔雨水算起的,可见《符天历》在唐宋之际星命术和民间历术中有相当广泛的使用。

4 《星学大成》所载十一曜行度算法中的积日和《符天历》历元

在明代万民英编撰的《星学大成》卷14《三辰通载》中收录了计算十一曜*日、月、五星构成七曜,加上罗睺、计都、月孛、紫气形成十一曜,也即所谓的“七政四余”体系。中国古代“七政四余”体系的形成和演变参见文献[17]和[18]中的分析和讨论。行度的“总龟算法”。其中的“木徳岁星总龟算法”为：“先置积日一十七万一千三百,减七十四,以周天三百九十八日八十八分六十一秒去之,看余日多少,入在何段,下太阳中定星度,又以余日数去之,不满者为定度。”([16],卷14)此处计算木星行度时,其积日数的算法是用171300的固定积日数减去调整积日数74,然后累减木星运行周期的天数,看最后不足减的余数落在木星运行周期的何段,来确定其行度。其余十曜的算法与此类似,只是具体参数有所不同,现把与本文讨论有关的积日数据整理成表1。

表1 《三辰通载》十一曜行度算法中的积日数据

因计都的“总龟算法”依赖于罗睺的计算结果：“将罗睺定度加半周天数”([16],卷22),所以表1中无独立的积日数据。

不难发现,从《符天历》的历元显庆五年正月壬寅雨水合朔(660年2月16日)开始算起,第171300日正好是宋建炎三年正月辛酉雨水(1129年2月12日,儒略日序为2133468)。此处积日的算法照例是首尾两日都算上。从显庆五年雨水到建炎三年雨水共469年的实际天数为171299天,因此《三辰通载》“总龟算法”计算太阳行度时调整积日数为减1日。

由上可知,《三辰通载》中“总龟算法”给出的十一曜行度计算法均以建炎三年正月雨水为近距历元,实际计算的时候加上或减去1日到一千多日不等的历元时刻修正。此算法的真正历元可上溯到《符天历》的历元显庆五年正月壬寅雨水合朔。这一点也意味着唐宋之际兴起的十一曜星命术与《符天历》有很密切的关系。

5 《九执历》的积日算法与《符天历》历元

本文第1节提到,孔庆典认为《符天历》使用《九执历》所载的积日算法,并运用该算法计算出日本《续群书类从》中所保存的一则天永三年《宿曜运命勘录》中的积日起点为显庆五年“正月三日雨水甲辰”——即其所认定的《符天历》历元。([6],163页)

《九执历》计算积日的方法记载在《开元占经》所录该历的“推积日及小余章”中,为方便下文讨论,摘录如下*摘录过程中校改了几处传抄错误的文字。：

上古积年数太繁广,每因章首,遂便删除,务从简易,用舍随时。今起明(显)庆二年丁巳岁二月一日,以为历首,至开元二年甲寅岁,置积年五十七算。术曰：置积年。以十二乘之,加自入年已来所积月。(假令推其年三月五日事,即历起二月一日为首,于十二乘讫,数上更加一算,即是加入年所经一个月了。)加讫,重张位下,以七乘之,恒加一百三十二,以二百二十八除之,得闰月。以闰月加上位,为积月,以三十乘之,加自入月已来所经日。(假令推三月五日事,即于三十乘讫,数上更加五算,即是加入月所经五日了。)重张位下位,十一乘之,恒加差四百二十九,以七百三除之,得自入历已来所经小月(梵云欠夜),不尽为小余。以小月减上位,为积日*从该段术文提供的算例(计算过程和结果见表2算例1)可知,该处的“积日”等于两个日期之间的儒略日序之差,与本文上文所引星命书和历日资料中的积日在含义上有差别,后者是指儒略日序差再加一日。。[19]

根据上述记载可知,《九执历》断取近距,以显庆二年丁巳岁二月一日己未(657年3月20日)为历元,并不难将以上文字叙述的积日算法转化为以下5式：

积年=所求年-历元年

积月=积年×12+自入年已来所积月+闰月

积日=积月×30+自入月已来所经日-小月

表2中的算例1以上述所引《九执历》术文中所举的开元二年甲寅岁三月五日壬辰(714年4月23日)为例,列出了中间计算结果和最后结果。结果显示,在《九执历》被编译出来的年代,《九执历》给出的求积日方法是有效的,与实际计数日子的方法是等价的。

表2 《九执历》求积日法算例三则1)

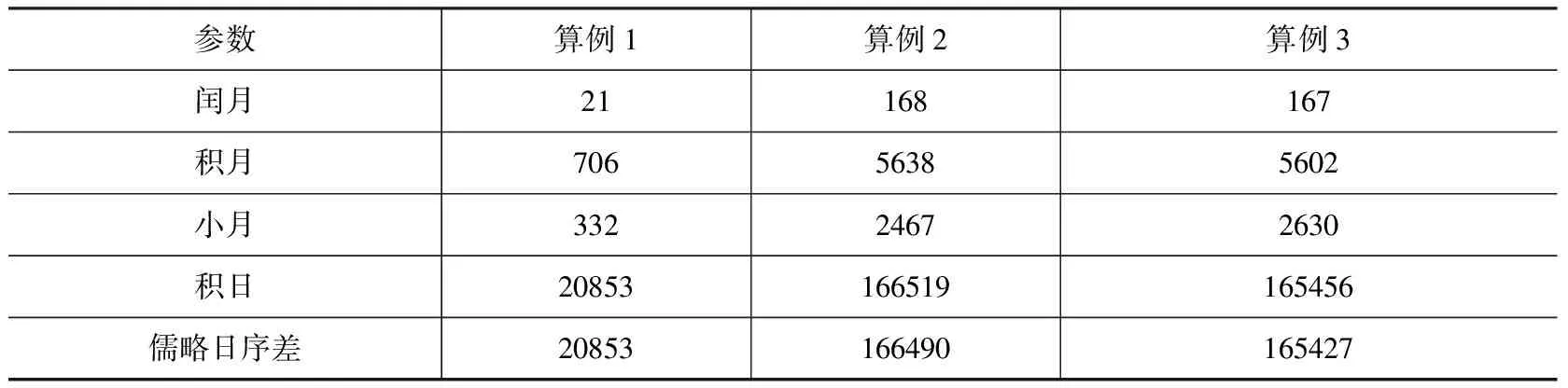
续表2

1) 表中加“*”号的求卜者生辰日期的归算详见本文第三节的讨论。

表2中算例2以《九执历》求积日法计算其历元到日本天永三年《宿曜运命勘录》中某求卜者生辰之间的积日,可以发现用《九执历》积日算法得到的积日数比实际计数日子所求得的天数少29日,即一个历法月的天数。查陈垣《二十史朔闰表》,从显庆二年二月一日到天永三年十二月二十六日之间共有167个闰月,比上述求得的168个闰月,正好少一个闰月。因此用《九执历》求积日法求得的积日数与实际计数日子的结果之间正好差一个月。

表2中算例3又以《九执历》求积日法来计算《符天历》历元到天永三年十二月二十六日之间的积日(这里需要注意历元日期从《九执历》的“二月一日”变为《符天历》的“一月一日”),所得结果比实际计数日子少29日,也是一个月的天数。查陈垣《二十史朔闰表》,从显庆五年正月一日到天永三年十二月二十六日之间共有166个闰月,比上述求得的167个闰月,正好少一个闰月。

由上可知,如果要用《九执历》中求积日的方法计算两个日期之间的天数,需要特别谨慎,尤其当两个日期相隔比较久远,其中实际的置闰情况可能与《九执历》所给方法求出的闰月数目不一致,这样求得的积日与实际的日数之间可能有一个月之差。

在了解了上述《九执历》求积日的方法、步骤和可能出现的偏差之后,再来看孔庆典计算天永三年《宿曜运命勘录》中积日的方法和过程,发现有如下问题：(1)在计算“积年”和“积月”时以公元1113年1月入算([6],162页),但彼时并无公历的概念,按照《九执历》计算“积年”、“积月”的方法,应取壬辰年十二月入算。(2)在计算“小月”和“积日”的时候,“加入月以来所经日”取“-2”日,其给出解释为“经归算后比历首日少3日”([6],181页注69),不知何意。无论取《九执历》的“二月初一”还是《符天历》的“正月初一”为历首日,均不能得到此结果。而“加入月以来所经日”的含义,从《九执历》原文所举例子可知,就是加上所求日在该月中的序数,无需归算。(3)孔文称“历首处在二月”([6],181页注68),说明其在计算天永三年《宿曜运命勘录》中的积日时所取的历元是《九执历》的历元“显庆二年丁巳岁二月一日”,但其又将计算所得的积日认为始于“显庆五年正月甲辰雨水”,即其认定的《符天历》历元。这样的处理显然矛盾重重。如果要在《符天历》框架内计算积日,那必定是要从《符天历》的历元算起。

综上,孔庆典得出的日本天永三年《宿曜运命勘录》中的积日始于“显庆五年正月甲辰雨水”的结论建立在错误的计算之上,是不成立的。《九执历》积日算法算得的积日数与实际计数日子所得的天数本应相等,并不存在一个“相差3日”的“系统误差”([6],181页注70)；只是在所求日远离历元时,确定闰月数的经验算法可能出现偏差；而像天永三年《宿曜运命勘录》这样的星命书中的积日数是指正常的民用日天数。

6 结 论

经过本文的讨论,可以确定《符天历》历元的确切日期是显庆五年庚申岁正月壬寅雨水合朔,对应公元日期为660年2月16日,对应的儒略日序为1962169。该结论解决了以往学者针对《符天历》历元“气朔不合”与“气朔相合”的争论,并与日本天永三年《宿曜运命勘录》所载积日数、东京大学“东京都六条有康氏所藏文书”中一则“宿曜御运录”所载积日数、俄藏黑水城汉文文献“X37刻本绍圣元年历书”残篇所载积日数相符合；同时,该历元日期还解释了《星学大成·三辰通载》十一曜行度算法所给出的总积日数171300,即为该算法所取近距历元建炎三年正月雨水距《符天历》历元的积日数。最后,通过对《九执历》积日算法的讨论可知,该算法至少在《九执历》被编译出来的年代是有效的,与实际计数日子所得结果是一致的；但当所求日远离其历元时,算得的闰月数目可能与实际置闰不一致,所求得的积日数可能与实际计数所得的日子有一个闰月的差异。已有的工作认为《符天历》历元始于“显庆五年正月甲辰雨水”,并以此推断《符天历》“气朔不合”,是错误地使用了《九执历》积日算法的结果,是无效的。

1 欧阳修. 新五代史·司天考第一[M]. 北京: 中华书局, 1974.

2 桃裕行. 符天曆について[J]. (日本)科學史研究, 1964,(71).

3 钮卫星, 江晓原. 中国古历中的近距历元及其印度渊源[C] // 江晓原, 钮卫星. 天文西学东渐集. 上海: 世纪出版集团, 上海书店出版社, 2001. 177～186.

4 薮内清. 关于唐曹士蔿的符天历[J]. 柯士仁, 译. 易树人, 校. 科学史译丛, 1983,(1).

5 陈久金. 符天历研究[J]. 自然科学史研究. 1986, 5(1): 34～40.

6 孔庆典. 10世纪前中国纪历文化源流——以简帛为中心[M]. 上海: 上海人民出版社, 2011.

7 陈垣. 二十史朔闰表[M]. 上海: 上海古籍出版社, 1956. 87.

8 王钦若, 等. 册府元龟校订本. 周勋初, 等校订. 南京: 凤凰出版社, 2006. 33.

9 陆心源. 唐文续拾[M]//董诰, 等. 全唐文. 第11册. 北京: 中华书局, 1983. 11330.

10 Standish M, et al. Planetary and Lunar Ephemeris DE404[CD]. JPL/NASA.

11 金俱叱. 七曜攘灾诀[M]//大正新修大藏经. 卷21. 东京: 大正一切经刊行会, 1924～1934. 450.

12 宿曜運命勘錄[M]//続群書類従. 第31輯上. 東京: 続群書類従完成会, 1926(大正十五年). 429.

13 宿曜御运录[M]//东京都六条有康氏所藏文书. 东京: 东京大学图书馆藏.

14 曹士蔿. 符天历经日躔差立成[M]//薄树人. 中国科学技术典籍通汇·天文卷一. 郑州: 河南教育出版社, 1995. 137.

15 中山茂. 符天曆の天文學史的位置[J]. (日本)科學史研究, 1964,(71): 120～121.

16 万民英. 三辰通载[M]//星学大成//景印文渊阁四库全书. 台北: 台湾商务印书馆, 1986.

17 钮卫星. 从“罗、计”到“四余”: 外来天文概念汉化之一例[J]. 上海交通大学学报(哲学社会科学版), 2010, 18(6): 48～57.

18 钮卫星. 唐宋之际道教十一曜星神崇拜的起源和流行[J]. 世界宗教研究, 2012,(1): 85～95.

19 瞿昙悉达. 开元占经[M]//薄树人. 中国科学技术典籍通汇·天文卷五. 郑州: 河南教育出版社, 1995. 873～874.

A Re-examination of the Epoch Date of theFutianLi

NIU Weixing

(SchoolofHistoryandCultureofScience,ShanghaiJiaoTongUniversity,Shanghai200240,China)

After investigating some previous research and related literature, it is concluded that the epoch date ofFutianLi(符天历) is the date renyin(壬寅), when the solar term of yushui(Rainwater) combined with the first day of the first month of the 5thyear of Reign Xianqing (显庆). Thisyushuiis a kind of ‘true solar term’ (定气) instead of ‘mean solar term’ (平气). Its corresponding Gregorian date is February 16, 660, and its Julian date is 1962169. A contradiction is thus resolved between the opinion that the ‘solar termyushuidoes not conform to the new moon’, which was held by some previous researchers, and the opposite point of view recorded in relevant literature. The conclusion is further examined by means of four records on the sum of days accumulated from theFutianLi’s epoch date, which are preserved in astrological and calendrical sources. Finally, after a detailed discussion on theJiuzhiLi’s method of calculating accumulated days from epoch, it is pointed out that theJiuzhiLi’s method does not support the argument of taking the third day of the first month of the 5th year of Reign Xianqing (February 18, 660) as the epoch date of theFutianLi.

FutianLi, epoch date, sum of days accumulated from epoch, true solar term

2016- 05- 02；

2016- 12- 20

钮卫星,1968年生,浙江湖州人,教授,主要从事天文学史研究。

上海市浦江人才计划项目《唐代中外天文学的交流与比较研究》(项目编号：15PJC068)

N092∶P1- 092

A

1000- 0224(2017)01- 0001- 09