船舶自动靠泊简捷非线性神经网络控制器

张 强, 张显库, 林南均

(1．大连海事大学 航海学院，辽宁 大连 116026； 2. 山东交通学院 航海学院， 山东 威海 264209； 3. 木浦国立海事大学 航海学院，韩国 木浦 530729)

船舶自动靠泊问题涉及船舶在浅水中的低速运动，风、浪、流的干扰相对较强，系统的信息量较大，操纵和控制船舶较为困难。[1]因此，有关船舶自动靠泊问题的研究隐含受限水域、不确定数学模型、较强环境扰动下的船舶操纵及定位控制等内容。[2]

为实现自动靠泊控制，在控制器设计中应用非线性滑模[3]、反步法[4]、最优控制[5]和神经网络等算法。由于人工神经网络(Artificial Neural Network，ANN)具有较强的非线性函数映射能力，且易复制船长丰富的靠泊经验，因此在解决自动靠泊控制问题时得到广泛应用。ZHANG等[6]利用多参数神经网络算法设计在线调参的靠泊控制器。IM等[7-9]和TRAN等[10]利用传统的神经网络算法设计并行神经网络靠泊控制器、基于运动识别的神经网络靠泊控制器、根据不同靠泊状态进行决策的神经网络控制器及利用侧推器和拖船等辅助设备的自动靠泊控制器。NGUYEN等[11]利用自适应神经网络分别训练舵、桨控制信号，实现自动靠泊。AHMED等[12-16]利用神经网络技术，结合虚拟窗口理论、非线性规划及PD混合控制等算法设计自动靠泊控制器，并利用自由船模试验验证其有效性。

随着海上信息技术的不断发展，基于大数据的靠泊控制参数整定逐渐成为可能。[17]在大量有效样本数据下，神经网络输入参数的优化会减少计算维数。因此，为实现自动靠泊控制，降低计算负荷，首先在ANN架构[9]的基础上，利用BP神经网络算法设计3层神经网络控制器。根据靠泊经验，通过取消虚拟导航线和位置辅助线参数，优化输入参数。其次，在4种船舶初始状态下进行训练，从而获取样本数据，训练网络权重和偏差。针对样本数据较多、计算负荷大的问题，根据样本有效数据信息量与控制器输出成正比的关系，对有效信息量较大的数据(例如舵角或螺旋桨转速变化较大时的数据)增大提取频率，而对有效信息量少的数据减小提取频率，从而优化有效样本数据，缩短计算时间。最后，利用基于MMG(Maneuvering Modeling Group)船舶数学模型的靠泊仿真试验，验证船舶在不同于样本数据的初始状态下达到理想的控制效果，从而进一步验证简捷神经网络靠泊控制器在减少计算维度时的控制有效性。

1 船舶靠泊非线性数学模型

在充分考虑船舶靠泊等操纵实践的基础上，借鉴MMG分离建模的思想，采用惯性坐标系O-xyz和附体坐标系O′-x′y′z′(见图1)，其中：X，Y，N分别为作用在船舶上的合外力在附体坐标系上的投影；u，v，r分别为船舶纵向速度矢量分量、横向速度矢量分量和转艏角速度；δ，Ψ，β分别为舵角、航向角和漂角。采用的数学模型为

(1)

式(1)中：m为船舶质量；mx，my，Jzz分别为附体坐标系上船舶纵向附加质量、横向附加质量和附加惯性矩；Izz为船体绕z0轴的转动惯量；YxC重心力矩修正；H，P，R，W，C分别为船体、桨、舵、风、流。

2 自动靠泊原理

船舶自动靠泊通常有泊位外镇定、直接靠拢和先泊位外镇定再平行靠拢等3种类型。[2]大型船舶自主靠港操纵一般分为靠泊操纵和系泊操纵2个阶段。

1)靠泊操纵为船舶由外海减速至泊位外当，使船体尽量平行于泊位或有利于系泊的位置，并控制船位至撇缆绳能打到泊位或带缆艇能拖带缆绳上岸桩的位置。此时船速尽可能小。

2)系泊操纵是船舶综合利用舵、桨、缆绳、锚链及侧推器等设备，实现船舷与泊位碰垫完全靠拢。

然而，大部分大型船舶都要借助拖船等辅助手段靠泊。参考文献[7]～文献[9]，本文设计的控制器主要应用在大型船舶靠泊操纵的第一阶段，控制目标是使船速减小到0.1 m/s以内，航向保持在泊位方向±20°以内，船位距离泊位1倍船长以内。

AHMED等[13]认为船舶沿虚拟导航线航行至距离码头1.5倍船长的泊位外档处镇定，即完成自动靠泊控制任务。虚拟导航线是大多数船长靠泊时导引船舶抵达泊位的航线，与码头岸线的夹角一般为30°(见图2)。然而，在实际靠泊过程中，虚拟导航线是根据不同泊位的地理条件和外界干扰随时调整的，并非固定的航线。由于欠驱动船舶在低速时并不能完全跟踪设计的航线，且虚拟航线有时会给船长或引航员带来干扰，从而影响船舶安全靠泊，因此在进行训练样本时取消虚拟导航线。

3 ANN控制器设计

本文设计的自动靠泊控制器(见图3)是利用ANN直接学习的方法得到的。首先，由有经验的船长在已知初始条件下操纵具有舵机特性和螺旋桨特性的MMG船舶数学模型进行实际靠泊，从而获得训练数据。随后，利用多层神经网络设计控制器，并采用BP算法训练网络权重和偏差。最后，利用ANN的泛化性能，在不同初始输入条件下实现船舶自动靠泊控制的输出。

网络训练的目标是减小样本训练输出和控制器输出的误差。设3层ANN中各层的节点个数分别为m，n，p，训练数据以{q1,o1}, {q2,o2},…，{qi,oi}的形式存储，其中qi及oi为神经网络输入和目标输出。在隐层的n个节点处，其输出Hn可表示为

(2)

式(2)中：f1和Nn分别为隐层的激活函数及网络N的n个节点的输入；Wmn和bn分别为节点n到m的权重及隐层Hn的阈值。隐层的活化函数选择Tansig函数，即

(3)

同理，在输出层第p节点的输出可表示为

(4)

式(4)中：f2和Np分别为输出层的活化函数及输出层p节点的输入；Wnp和bp分别为p节点到n节点的权重及输出层Op的阈值。在隐层的传递函数选择Satlin函数，即

(5)

目标函数表示为

(6)

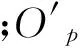
Wk+1=Wk-[JT(Wk)J(W)+μI]-1JT(Wk)E(Wk)

(7)

式(7)中：Wk包括神经网络的所有权重；J为雅克比矩阵；I为辨识矩阵；μ为调整系数。

输入层由输入的特征决定，在进行ANN模型设计时，若将对模型贡献较小的参数引入到网络中，势必会造成网络瘫痪，影响网络收的敛速度，且易于使网络陷入局部极小；同时，当外推这组学习输入/输出数据时，预测结果的正确率也没有保证。[19]在文献[9]中，8个与靠泊有关的输入参数分别为y0，x0，Ψ，u，v，r，d1，d2。由于船位信息包含船位到坐标横轴的距离x0和纵轴的距离y0及船位到虚拟导航线的辅助坐标参数d1和d2，而后者相当于x0和y0的坐标变换。考虑到实际靠泊中d1和d2的必要性不足(第2部分自动靠泊原理中已论述)，且对模型的贡献较小，因此采用与靠泊直接相关的6个参数，减少2个计算维度。ANN三层网络架构见图4，其中：输入层有6个输入参数，分别为y0，x0，Ψ，u，v，r；隐层节点数为25个；输出层有2个输出参数，即舵角δ和螺旋桨转速n。

最终t+1时刻的控制律[δt+1,nt+1]T表示为

Ψ(t),ut,vt,rt]T+bn)+bp)

(8)

4 ANN参数训练

以一艘液化气船[18]作为仿真对象，在MATLAB环境下利用MMG船舶运动数学模型(1)和GUI控件搭建靠泊仿真平台。液化气船仿真参数见表1。

在参数训练中，凭借多年的船舶操纵经验，利用搭建的靠泊仿真平台，在不同的初始条件下操纵船舶，针对舵角δ和螺旋桨转速n进行多次靠泊试验。试验后，剔除靠泊过程中不理想的样本点数据(1个样本点数据包含某时刻的船舶运动、舵角和螺旋桨转速数据)，仅保留最优样本点数据，例如剔除船舶靠泊速度过大或最终船位距离目标点较远的数据。为方便处理，在进行样本训练时，需对输入/输出数据进行归一化；在实际操作中，取预测参数的最大值为1，最小值为0，中间值利用加权平均法计算。仿真中设置训练采样步长为0.2 s，在1次完整的靠泊过程中的采样数据较多，为优化样本质量，根据有效信息量调整提取频率。

表1 液化气船仿真参数

4.1 样本数据

为提高样本数据的有效性，设计4种不同的初始船位进行靠泊训练，获得大量具有多样性的样本数据。初始状态的参数为(y0/L，x0/L，Ψ，u，v，r，n，δ)，4组具体值为:(5，6，240，2，0，0，0.75，0)；(5，6，220，2，0，0，0.75，0)；(3，6，260，2，0，0，0.75，0)；(3，6，240，2，0，0，0.75，0)。由于本文主要验证输入参数优化后的控制器的有效性，因此仿真环境中的外界干扰只考虑风速为5 m/s，风向为270°的情况。为使靠泊效果明显，保证靠泊安全，仿真坐标系的原点取在泊位横向外当0.5倍船长处。训练后的样本数据见图5。

由图5可知，在4种初始状态下均能完成靠泊任务。以初始状态(1)为例，其参数见图6。

4.2 参数训练

利用样本数据进行权重和偏差训练。由于在样本训练中产生大量的样本数据，为优化数据和简化计算，在提取样本数据时根据样本数据信息量与控制器输出成正比的关系，对有效信息量较大的时间段增大提取频率，例如图6中的500～600 s时间段，若舵角或螺旋桨转速变化较大，则平均时间间隔内提取100%或80%的数据；而对有效信息量较小的时间段减小提取频率，因为该部分包含的有效信息较少，例如在100～240 s时间段内，平均时间间隔内提取10%的数据。

在进行网络训练时，设定训练目标最小误差为0.000 1，最大迭代次数等于样本数量。数据归一化处理后的训练结果见图7，其中：横坐标为时间；纵坐标为归一化后的舵角和螺旋桨转速；训练前的初始数据为随机数据，训练后的数据与样本数据符合度较高，说明参数训练有效。

5 仿真结果

利用训练好的ANN，在初始状态参数为(4，6，250，2，0，0，0.75，0)的条件下进行自动靠泊控制仿真，其他仿真环境与参数训练时一致。仿真结果见图8。控制器能使船舶较好地完成控制任务。

由图9可知，船速从2 m/s下降到接近0.068 m/s，达到<0.1 m/s的目标，且下降速率较为平稳，横向速度为-0.003 m/s，转艏速度为0.001 m/s。最终横向船位坐标在0.04L处，纵向船位坐标在-0.07L处，非常接近目标船位，误差较小。最终靠泊时艏向为250°，最佳目标艏向为270°，误差为-20°。虽然未能达到270°，但也符合航海实践要求(实践中有时使艏部先接近泊位，以便带艏缆或艏倒缆)。存在误差的原因主要有：

1)在自动靠泊仿真中，为检验所提出算法的泛化性能，采用的初始位置与训练位置不同，导致误差存在。

2)在设计4种不同的初始船位进行靠泊训练时，各次手动靠泊的样本数据之间也存在一定的差异，影响自动靠泊的精度。

相比图6中第1种初始状态下的训练数据，图9中纵向船速u下降较快，虽然舵角δ较大，但由于船速相对较小，造成转艏力矩较小，从而使航向未能达到270°，但这满足航海实践的要求。

在282～325 s及605 s以后，使用右满舵信号，以控制航向、摆正船位。螺旋桨转速变化较为平缓，整个靠泊时间为706 s，满足航海实践的要求。控制结果显示设计的控制器能达到预期的控制效果。

6 结束语

为利用ANN实现自动靠泊，减少计算维度，降低计算负荷，本文利用BP神经网络算法设计3层神经网络控制器，并根据实际靠泊操纵经验对神经网络输入参数进行优化。在大样本数据处理中，采用选择性有效数据提取方法优化控制效果，缩短计算时间。通过基于MMG的数学模型的靠泊仿真试验，验证了该控制器不仅能在不同于样本数据的初始状态下减少计算维数、降低计算负荷，还能达到较为理想的控制效果，满足航海实践的要求。

此外，本文提出的ANN模型不依赖具有不确定因素的虚拟导航线，可在实际控制过程中降低计算负荷，提高控制的实时性，为后续自动靠泊的在线ANN控制提供理论支撑。

[1] 张显库. 船舶运动简捷鲁棒控制[M].北京:科学出版社, 2012：5.

[2] 张强，张显库. 船舶自动靠泊研究综述[J]. 大连海事大学学报， 2015, 41(3):1-9.

[3] 卜仁祥,刘正江,胡江强. 欠驱动船舶非线性滑模靠泊控制器[J]. 交通运输工程学报，2007, 7(4):24-29.

[4] PARK J Y, KIM N. Design of an Adaptive Backstepping Controller for Auto-Berthing a Cruise Ship Under Wind Loads[J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6(2):347-360.

[5] MIZUNO N, UNCHIDA Y, OKAZAKI T. Quasi Real-Time Optimal Control Scheme for Automatic Berthing[J]. IFAC Papers Online, 2015, 48(16):305-312.

[6] ZHANG Yao, HEARN G E, SEN P. A Multivariable Neural Controller for Automatic Ship Berthing Control Systems[J]. IEEE Control Systems, 1997, 17(4):31-45.

[7] IM N K, HASEGAWA K. A Study on Automatic Ship Berthing Using Parallel Neural Controller (2nd Report)-Motion Identification Considering Lateral Speed and Angular Velocity to Cope with Disturbances[J]. Journal of the Kansai Society of Naval Architects Japan, 2001, 237(3):127-132.

[8] IM N K, HASEGAWA K. Motion Identification Using Neural Networks and its Application to Automatic Ship Berthing Under Wind[J]. Journal of Technology, 2002, 6(1): 16-26.

[9] IM N K, LEE S K, DO B H. An Application of ANN to Automatic Ship Berthing Using Selective Controller[J]. International Journal on Marine Navigation and Safety of Sea Transportation, 2007, 1(1):101-105.

[10] TRAN V L, IM N K. A Study on Ship Automatic Berthing with Assistance of Auxiliary Devices[J]. International Journal of Naval Architecture and Ocean Engineering, 2012,4(3):199- 210.

[11] NGUYEN P H, JUNG Y C. Automatic Berthing Control of Ship Using Adaptive Neural Networks[J]. International Journal of Navigation and Port Research, 2007, 31(7):563-568.

[12] AHMED Y A, HASEGAWA K. Automatic Ship Berthing Using Artificial Neural Network Based on Virtual Window Concept in Wind Condition[C]//IFAC Symposium on Control in Transportation Systems, 2012,45(24):286-291.

[13] AHMED Y A, HASEGAWA K. Automatic Ship Berthing Using Artificial Neural Network Trained by Consistent Teaching Data Using Nonlinear Programming Method[J]. Engineering Applications of Artificial Intelligence, 2013, 26(10): 2287-2304.

[14] AHMED Y A, HASEGAWA K. Experiment Results for Automatic Ship Berthing Using Artificial Neural Network Based Controller[Z]. IFAC Proceedings Volumes, 47(3): 2658-2663.

[15] AHMED Y A, HASEGAWA K. Artificial Neural Network Based Automatic Ship Berthing Combining PD Controlled Side Thrusters[C]//13th International Conference on Control, Automation, Robotics & Vision. Singapore, 2014.

[16] AHMED Y A, HASEGAWA K. Consistently Trained Artificial Neural Network for Automatic Ship Berthing Control[J]. International Journal on Marine Navigation and Safety of Sea Transportation, 2015, 9(3):365-368.

[17] 黄泽洋，邵哲平，潘家财，等. 基于AIS的大型船舶靠泊航速分布规律[J]. 中国航海, 2016, 39(2): 55-58.

[18] ZHANG Qiang, ZHANG Xianku, IM NK. Ship Nonlinear-Feedback Course Keeping Algorithm Based on MMG Model Driven by Bipolar Sigmoid Function for Berthing[J]. International Journal of Naval Architecture and Ocean Engineering, 2017，9(5):525-536.

[19] 高大文，王鹏，孙丽欣，等. 人工神经网络输入层节点筛选规则的确定[J]. 高技术通讯，2002, 12(6):65-68.