C-Gorenstein模与Gorenstein模

张 珍，陶琳琳

（淄博师范高等专科学校 初等教育系，山东 淄博 255130）

C-Gorenstein模与Gorenstein模

张 珍，陶琳琳

（淄博师范高等专科学校 初等教育系，山东 淄博 255130）

在这篇文章中，我们介绍了平凡扩张环R∝C，其中C是一个半对偶化模.我们得到，当R是非诺特环时，内射模和C-内射模是C-Gorenstein内射的，平坦模和C-平坦模是C-Gorenstein平坦的。并且C-Gorenstein内射R-模是Gorenstein内射R∝C-模，以及C-Gorenstein投射R-模是Gorenstein投射R∝C-模，C-Gorenstein平坦R-模是Gorenstein平坦R∝C-模。

半对偶化模；平凡扩张环；C-Gorenstein投射模

整篇文章中，R始终代表一个有单位元的结合环，C是一个半对偶化的R-模。早在很久以前，很多作者就研究了半对偶化模这个概念，不过他们并没有用“半对偶化模”这个名字。Foxby称这样的模为秩为 1的 PG-模；Golod称之为 suitable-模；Vasconcelos称其为spherical-模.

总的来说，这类模是对偶化模和秩为1的自由模的推广.由半对偶化模诱导的相对代数引起了海内外大量专家和学者的重视.有了它，经典的投射模被推广成C-投射模；内射模被推广成C-内射模；平坦模被推广成C-平坦模.并且，Gorenstein投射（内射、平坦）模被推广成C-Gorenstein投射（内射、平坦）模等等，从而产生了由半对偶化模诱导的同调代数，这一方面的内容请参看文献。［6、7、8］

在经典的同调代数中，我们用投射（内射、平坦）模来分解一给定的R-模，得到该模的投射（内射、平坦）维数，这些同调维数可以来刻画环。利用同样的方法，许多作者研究了Gorenstein同调维数，从而更好地刻画了Gorenstein环.自然的，我们想考虑由半对偶化模C诱导的同调维数和 Gorenstein同调维数，用它们来研究C诱导的Gorenstein环.我们知道环R叫做n-Gorenstein环如果它是左右诺特的并且R的自内射维数小于等于n。因为半对偶化模C是R的推广，所以我们想研究一下当C的内射维数小于等于n时，环R会有一些什么性质.

本文包括两节，第一节我们给出了一些用到的定义和符号。第二节证明了一些主要的结论.

1.预备知识

定义1.1.［6］（P171）设X是由R-模构成的子范畴.对于任意R-模M，

（1）M的左X-预解式是指一个正和序列：

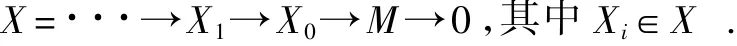
（2）M的右X-预解式是指一个正和序列：

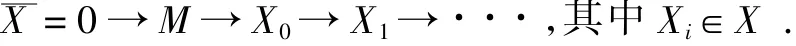
模M的X投射维数是指这样一个数：X-pdM =inf{sup{n≥0|Xn≠0}|X 是M的左X预解式}；类似的，我们可以定义 M的X内射维数及X-平坦维数.

本文中我们用pd（M），id（M），fd（M）分别代表M的投射、内射和平坦维数.用Gpd（M），Gid（M）和 Gfd（M）分别代表 M的 Gorenstein投射（内射、平坦）维数.

定义1.2.一个R-模C称作半对偶化的，如果它满足下列三个条件：

（1）C有一个有限生成的投射模构成的预解式；

（2）C是自正交的，即：Ext≥1（C，C）=0；

（3）Hom（C，C）≅R.

假设C是一个半对偶化R-模，我们分别用FC，PC和IC来代表所有的C-平坦、C-投射和C-内射R-模类，即：

（1）FC={C⊗ F/F是一平坦模}；

（2）PC={C⊗ P/P是一投射模}；

（3）IC={Hom（C，E） /E是一内射模}.

通过FC，PC和IC，Holm and JÂrgensen在交换诺特环上分别定义了由C诱导的C-Gorenstein平坦，投射和内射模［1］。很明显，这三类模推广了Holm的Gorenstein平坦，投射和内射模。White在一般的交换环上定义了C-Gorenstein投射模，并称之为-投射模.

根据 Definition 9［1］，对任意R-模M，我们分别用C-Gpd（M）、C-Gid（M）和C-Gfd（M）来表示M的C-Gorenstein投射、内射和平坦维数.

最后，我们给出平凡扩张环的定义：

定义 1.3.设R是任意环，C是任意R-模。我们对R⊕C的元素定义乘法如下：

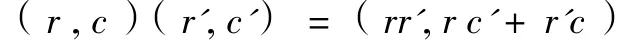
从而R⊕C成为一个环，称为由环R和模C构成的平凡扩张环，记为R∝C.

环R和R∝C之间存在自然的环同态，从而我们可以把任意R-模看成是R∝C-模，也可以把任意R∝C-模看成是R-模.

2.主要结果

定义 2.1.设R是一个交换诺特环，C是一半对偶化R-模，如果对于任意非负整数n有id（C）≤n，则称环R是n-C-Gorenstein环.

注 2.2. 根据［8］，如果R是诺特环，那么平凡扩张环也是诺特的.并且由Theorem 4.3.2［8］知，idR∝C（R∝C）=id（C）。因此R∝C是n-Gorenstein环.

为了证明我们的主要结论，我们首先证明下列命题。

命题2.3

（1）每一个内射模和C-内射模都是C-Gorenstein内射的；

（2）每一个投射模和C-投射模都是C-Gorenstein投射；

（3）每一个平坦模和C-平坦模都是C-Gorenstein平坦的.

证明：（1）由定义1.2知，半对偶化模C有一个有限生成的投射预解式：

显然它是Hom（C，-）正和的。因此我们得到这样的正和列：

对任意内射模I，用Hom（-，I）作用上述正和列得到

···→Hom（C，In1）→Hom（C，In0）→I→0对于内射模E，因为E∈BC（R），由C诱导的Bass类，所以C⊗Hom（C，E）≅E对任意的i≯0，我们有下列同构：

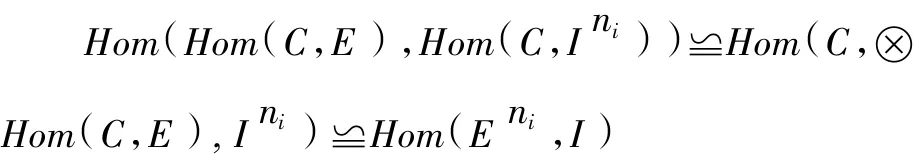
从而，用Hom（Hom（C，E），I）作用到上述正和列，我们得到

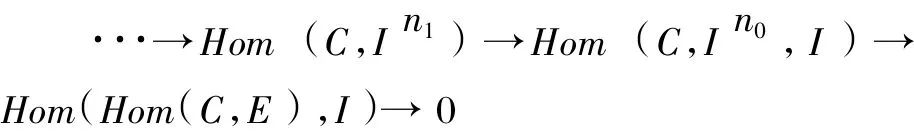
因为存在正和列0→Hom（C，I）→Hom（C，I）→0，很容易证明Hom（C，I）是C-Gorenstein内射的.

（2）和（3）可以类似于（1）来证明.

在定理 2.16［11］中，Holme证明了任意的CGorenstein内射R-模是Gorenstein内射R∝C-模，并且任意的C-Gorenstein投射R-模是Gorenstein投射R∝C-模.注意到他们要求R是一个诺特环.下面，我们将证明在一般的非诺特环上也有这样的结论.

命题 2.4：设R是任意交换环。对任意R-模M和内射R-模I，我们有

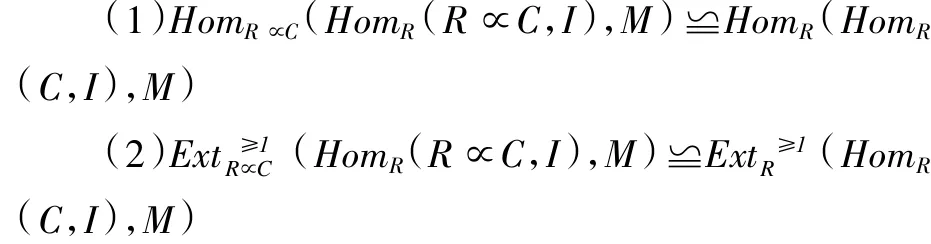
证明：因为存在R-模同构：R∝C≅R⊕C，所以R∝C存在有限生成的投射预解式.因此我们存在下列同构

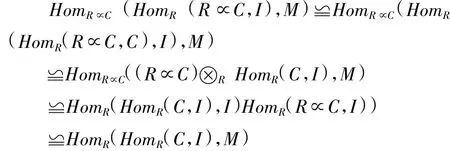
其中，第二个同构是根据定理3.2.11［2］，第三个同构是Hom-Adjoint同构.

（2）考虑HomR（C，I）的投射分解

因为 HomR（C，I）∈AC（R），所以Tor≥1（R∝C，因此我们用R∝C⊗R-作用，得到下列正和列

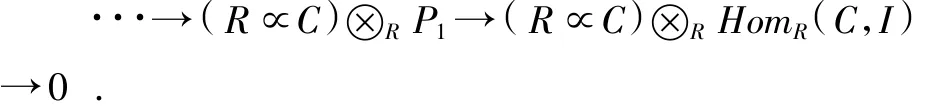
由 Lemma 3.1（3）［3］，对于任意的j≥0，（R∝C）⊗RPj是投射的R∝C-模.因此上述正和列是R∝C-模（R∝C）⊗RHomR（C，I）的投射分解.从而我没有下列同构：

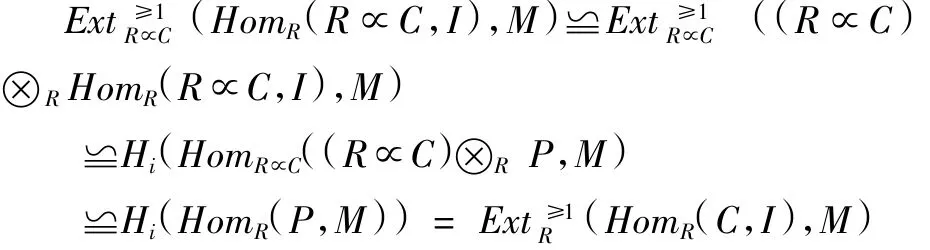
根据定理4.32［3］，我们得到C-GidR（M）=GidR∝C（M）.

注 2.5类似于上述命题的证明，我们得到 CGpdR（M）=GpdR∝C（M），以及C-GfdR（M）=GfdR∝C（M）.

［1］H.Holm，P.J{O}rgensen，Semi-dualizing modules and related Gorenstein homologica dimensions［J］.J.Pure Appl.Algebra.2006，205（2），423-445.

［2］E.E.Enochs and O.M.G.Jenda，Relative homological algebra［M］.（de Gruyter，Exp.Math 30，2000）.

［3］H.Holm，Gorenstein homological dimensions［J］.J.Pure Appl. Algebra 2004，189，167-193.

［4］H.-B.Foxby，Gorenstein modules and related modules［J］. Math.Scand.1972，31，267-284.

［5］H.Holm，P.J{O}rgensen，Cohen-Macaulay injective，projective，and flat dimension［J］.preprint，2004，vailable from http://www.arxiv.org/abs/math.AC/0405523.

［6］E.S.Golod，G-dimension and generalized perfect ideals［J］. Trudy Mat.Inst.Steklov，1984，165，62-66.

［7］W.V.Vasconcelos，Divisor theory in module categories［M］. North-Holland Publishing Co.，Amsterdam：Noth-Holland Math.Stud，（1974）.

［8］R.M.Fossum，P.A.Griffith，I.Reiten，Trivial extensions of abelian CategoriesM］.Berlin,Springerverlag（1975）.

（责任编辑：胡安波）

In this paper，we introduce the trivial extension ring of R by C，where C is a semidualizing module.We find that when R is non-Noetherian，the injective and C-injective R-modules are CGorenstein injective R-modules，flat and C-flat R-modules are C-Gorenstein flat R-modules.Moreover，we get that C-Gorenstein injective R-modules are Gorenstein injective R∝C-modules，C-Gorenstein proj-ective R-modules are Gorenstein projective R∝C-modules.

semidualizing module；trivial extension ring；C-Gorenstein projective module.

0154

A

（2017）01-0045-03

2016-12-07

张珍（1982-），女，山东菏泽人，博士，淄博师范高等专科学校初等教育系教师，主要从事同调代数方向的研究。陶琳琳，女，山东淄博人，淄博师范高等专科学校初等教育系教师。

注：本文系山东省自然科学基金项目“半对偶化模诱导的同调代数的有关研究”［ZR2015PA001］的阶段性研究成果。