激趣生疑 主动建构
——人教版第11册《数与形》的教学设计及反思
■ 武汉市江汉区航空路小学 余 莉
激趣生疑 主动建构
——人教版第11册《数与形》的教学设计及反思
■ 武汉市江汉区航空路小学 余 莉
《数与形》是人教版九年义务教育第十一册P107第八单元《数学广角》的内容。作为教材新增的内容,我考虑最多的还是目标的定位问题。按照传统的教学,例2以及后面编排的几道习题都属于思考题甚至竞赛题,是供学有余力的学生学习的,对普通学生来说要求偏高。现在教材作为例题编写,在教学中究竟该达到怎样的要求还需进一步分析和把握。在以前的学习中,也曾出现过一些有关数与形的练习,如在第一学段要求学生通过观察形,发现其中的一些规律,并解决简单的问题。可以说,学生结合“形”来分析问题还是有一定基础的。但纵观教材,并没有系统地安排教学数与形结合的内容,所涉及的练习也比较分散。因此,我理解这节课的安排是试图通过一道特殊的分数加法的计算,让学生进一步体会数与形之间的内在联系,借助“形”沟通加法与减法的关系,理解“无限接近1”的含义,同时把数形结合的思想迁移应用于解决其他一些实际问题,帮助学生积累相关知识经验。
【教学设计】
教学内容:人教版《义务教育教科书·数学》六年级上册P107例2,练习二。
教学目标:一是让学生经历观察、操作、归纳等活动,帮助学生借助“形”来直观感受与“数”之间的关系,体会有时“形”与“数”能互相解释,并能借助“形”解决一些与“数”有关的问题;二是培养学生通过数与形结合的方法来分析思考问题,从而感悟数形结合的思想,提高解决问题的能力。
教学重点:借助“形”(面积模型、线段图、直角坐标系等)感受与“数”之间的关系,培养学生用“数形结合”的思想解决问题。
教学难点:让学生体会极限思想。
教学用具:多媒体课件,投影仪。
【教学过程】
一、案例分析
人教版《义务教育教科书·数学》六年级上册第107页教学例2(题略)。
(一)沟通分数加减法的联系
师:这个算式的结果是多少?算算看。你是怎么想的?还有不同的想法吗?引出
2.借助图形感受加法与减法的联系

师:这个算式在图中表示什么?(要求的结果就是涂色部分的面积)
(二)渗透极限思想
如果不停地加下去,课件呈现:

2.请用“形”来解释这个结果(学生操作,展示)
3.反馈(看大屏幕)

(三)练习
“0.9+0.09+0.009+…”
结果是多少?能用“形”来解释这个结果吗?
小结:数与形的联系非常紧密。生活中我们有很多问题通过画图来解决会更直观。
二、习题练习
小兰和爸爸、妈妈一起步行到离家800m远的公园健身中心,用时20分钟。妈妈到了健身中心后直接返回家里,还是用了20分钟。小兰和爸爸一起在健身中心锻炼了10分钟。然后,小兰跑步回到家中,用了5分钟,而爸爸是走回家中,用了15分钟。
下面几个图哪个是妈妈离家的时间和离家距离的关系?哪个是描述爸爸的?哪个是描述小兰的?
(一)读题
同学们看懂了吗?题目主要讲了一个什么事情?
(二)课件呈现一张图
提问:你觉得这幅图表示的是谁的行走示意图?(妈妈)
追问:为什么?

(三)课件呈现其余两张图
提问:你觉得下面的两个示意图,哪个是小兰的,哪个是爸爸的?

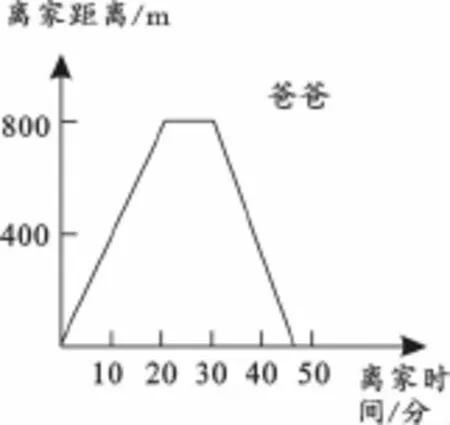
小结:有时候图可以帮助我们直观地解决问题,有时候也能帮助我们分析问题,理清题目意思。
三、拓展与延伸
(一)想一想
为什么“a×b+a×c=a×(b+c)”?请画图来解释。
1.同桌交流
2.独立完成并反馈
(二)习题训练
如下图,正方形的边长是a,如果边长增加b,使它变成一个更大的正方形,现在面积是多少?

四、课堂总结
今天这节课我们主要学习了什么?你有什么收获?
【教学反思】
新课标倡导:“教师在教学过程中应与学生积极互动、共同发展,引导学生质疑、调查、探究,使每个学生都能得到充分的发展。”“数与形”一课,我便紧紧围绕这一新的教学理念,设计了上面所列的教学流程。为达到课前预设的教学目标,我在具体的教学过程中力求做到以下几点。
1.借助图形沟通关系,体验数形结合的好处
在教学中,如果我们只是简单地让学生通过算式本身去发现规律,学生学起来会有一定的困难。因此,要给学生提供一种桥梁来帮助学生理解抽象的教学问题,而图形正是一种有效的桥梁。六年级上册第107页例2的教学就是如此,通过图形直观的表征,让学生更加清晰发现“”和“”求的都是同一个阴影部分的面积,从而让学生直观地看到了加减法算式之间的联系。通过追问,“如果按照这样的规律继续加下去,会怎样?”可以引出:之后,再引导学生通过观察、猜想、操作、验证等继续借助直观图象帮助学生理解越来越接近1,感悟极限思想。
2.借助图形理清思路,提高解决问题的能力
在本课的配套的练习中,题目中蕴含的信息量较大,直接让学生来读懂题意有一定的难度。因此在教学中,我试着引导学生通过结合图形来分析题目意思,理清数量之间的关系,提高解决问题的能力。如:P109练习22第五题“运行图”的教学,就是直接出示题目,先让学生自己自由读题,然后出示图形引导学生从“形”的角度来理解题意,在搜集题目中的关键信息来解释图形的过程中,培养学生利用图形分析问题、解决问题的意识和能力。
3.创设情境,导入新课
高昂的兴趣是学生学习的内动力,情境的创设使学习成为学生自觉的活动,让他们能独立尝试猜想,大胆验证猜想。
(1)情境引入
运用多媒体课件出示第108页例2的情境图,让学生大胆猜测,得出不确定的答案,从而激发学生探究新知的欲望。
(2)大胆猜想
课件出示题目的条件,小组合作,共同找出猜想的方法。
(3)小组汇报
(4)实施验证
对学生提出的猜想方法进行验证,教师要根据学生的回答适时地对解法进行归类并板书。
(5)总结方法
这一环节是教学的关键,首先。要鼓励学生合情合理地猜想,特别是引导学生思考每一小组的猜想是否有道理;其次,在猜想的基础上引导学生进行验证;最后,选择出最适合的方法。经历实践感悟、体验的过程,学生就能掌握计算此类题型的规律。
4.精选学习材料,适度处理和拓展教材内容
与第107页教学例2配套的几道练习题,我们曾对两个班66人进行了前测,在教师不作任何提示的情况下,独立作业40分钟时间,结果如下:
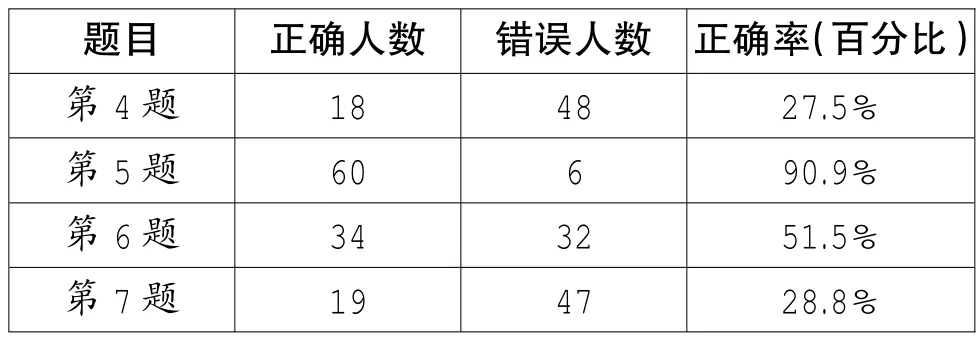
题目 正确人数 错误人数 正确率(百分比)第4题 18 48 27.5%第5题 60 6 90.9%第6题 34 32 51.5%第7题 19 47 28.8%
之所以出现上面的结果,我们认为,是因为这些题目与例2的结构相差较大,题目信息量丰富,给学生审题带来较大的困难,所以我们就补充了一题与第107页教学例2关联度和结构相匹配的题目“0.9+0.09+0.009+…”作为补充练习,同时把以前学过的“乘法分配律公式”和以后要学的“完全平方公式”作为本节课的拓展延伸,让学生再次感受“数形结合”的思想。
责任编辑 廖 林

