基于问题的初中数学复习课设计思考

唐海燕

摘要：本文以九年级《直角三角形的性質复习》为例，细谈如何借用数学例题设计课堂中的问题，用设问来梳理知识，用追问来整理方法，用反问来升华知识，从而实现有效复习的目的。

关键词：问题；有效复习；初中数学

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2017）02-0004

提问在课堂教学中具有独特的作用与功能，设计良好的提问能提示学生学习的重点和难点，能激发学生思维，了解学生听课的质量，培养学生的参与能力等。因此，课堂中的问题设计就显得举足轻重。

目前初中数学复习课还存在很多误区：如只对知识的单纯重复，或盲目拔高，没有明确的教学目标，习题设计鱼目混珠，实效性堪忧。如何走出这些误区，提高复习课的有效性呢？笔者结合自己的教学实践，谈谈对问题的初中数学复习课设计思考。

一、设问梳理知识

现在的数学复习课，教师大都为了节省时间，没有让学生通过自己对知识的回顾和梳理来理解归纳知识点，而过分急于求成，给出通过事先预想好的知识结构框架图，让学生填空或回答，这样的复习梳理不但不能有效地使学生复习知识点，更不能帮助学生提高与发展。

学生的思绪如泉水般涌现，他们争先恐后地举手发言。

本设计中，借用题目进行设问，问题起点低，并且具有一定的灵活性和开放性，学生不仅要通过检索已有的知识，而且还要利用知识解决问题。在问题的解决过程中，从而带动学生梳理知识点，激发学生的认知内驱力。

二、追问整理方法

追问就是教师根据知识的内在联系，设计以疑引疑、环环相扣的一系列问题进行提问。我们必须知道课堂中教师的追问目的是为了更多的思维火花被激发，缺乏了教师的追问，其实就是扼杀了学生自主思考的积极性。

案例：《直角三角形的性质复习》对比复习例题部分的设计：

例1： 如图，已知直角三角形ABC，∠ACB=90°，AC=6，BC=8，现将直角边AC沿直线AD折叠，使点C正好落在斜边AB上（点E），求CD的长。

学生思考片刻，根据折叠的性质，得到CD=DE，AC=AE=6，求解CD的长，马上想到设未知数。

那么，时机来了，教师追问：这样解设的目的是什么呢？

生1：可以利用构造方程的思想来求解。

不一会儿，就有学生举手示意已经解的答案了。

学生：根据已知和解设，可得BE=AB-AE=4，DB=BC-CD=8-x，利用折叠性质，可知∠CEB=90°，根据勾股定理，DE2+BE2=BD2，即x2+42=（8-x）2，解得x=3。

其他同学都点头表示赞许，大家很同意这样的解法过程。

由于这是九年级的复习课，于是教师顺势追问：你是利用方程思想方法解决这个问题，你还能有其他的思想方法吗？谁有不同的解法吗？

教师追问：那么从以上三位同学的方法看来，你有怎么样的反思？

生4：方法一体现了方程的思想，用勾股定理可以构造方程；方法二利用等积法，主要是很好地利用了直角三角形面积求解；方法三则是运用相似三角形的性质，方法不同，但结论相同。

教师再次追问：你觉得各有什么优点？

生5：方法一比较通用，但求解计算比较复杂；方法二需要高线，有一定的局限性；方法三运用相似比，计算简单。

本案例中，教师在例题中设计可以多方法解决的问题，有助于学生理解知识内在联系，由此及彼，拓宽思路。同时，训练巩固学生对方法的应用，特别是数学思想方法的提炼，这对培养优生思维极其有益，另一方面则有意无意地鼓励学生的独特性和多样化。

三、反问升华知识

复习的目的不仅是要使知识系统化，还要对所学的知识有新的认识，对解题的思想方法进行归纳或提炼，使知识升华，让不同层次的学生都有不同程度的提高。通过反问引导学生进行适当的分析和思辨，通过反问使学生经历问题的探究过程，通过反问使学生主动构建新的经验。

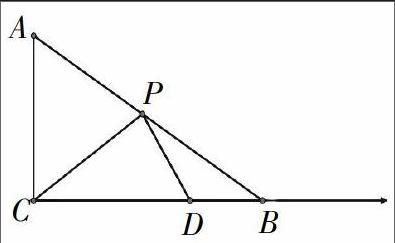
例2：如图，直角三角形ABC，∠ACB=90°，P是斜边AB上的一动点，连结CP，过点P作CP的垂线交CB（也可以是CB所在的直线）于点D。

第（1）问：当点P运动到斜边AB的中点时，求PD的长。

学生都可以准确地利用直角三角形斜边上的中线性质，结合相似三角形的性质列出比例式得到答案。

顺利解决第（1）问时，教师反问：因为点P是运动的，那么点P的运动会引起哪些线段的变化？你会关注哪些线段？

学生你一言我一语发表各自看法，这时候教师的另一个问题就顺理成章了：第（2）问：当AP为何值时，△PDB是等腰三角形。

当第（2）问时，由于惯性思维，学生将△PDB是等腰三角形分为三种情形进行讨论分析。随着分类思想的讨论开展，学生很快就会发现，其实不是按照△PDB是等腰三角形的分类进行，而是对点D的位置进行分类讨论。对△PDB是等腰三角形时，哪两边相等的情形也要进行说明。

生1：当AP为何值时，△PDB的面积是△ABC的1/4。

师：从面积的角度来提问，很不错，那么还有其他的角度吗？

生2：有没有一种可能性使△CPD是等腰直角三角形？

师反问：那么到底有没有这种可能性呢？你能说明理由吗？

生3：如果一开始，△ABC不是直角三角形，那么有没有其他更多的情况呢？

本案例中，学生在 “有问要提、有话可说、有理能辨”的数学课中碰撞着思维，闪耀着智慧的火花，彻底改变“满堂灌”式的“重结果、轻过程”的复习方式，数学课也因此充满了探索性、挑战性。

总之，本课以一个直角三角形贯穿课堂始终，在千变万化中，找寻知识的共性与异性，求同存异间又发现其实知识都是融会贯通的。摆脱简单的重复训练，脱离题海战术，实现了真正的有效复习、有效教学。