基于PSO优化的车辆稳定性研究

陈宇奇，陈家琪

(上海理工大学 光电信息与计算机工程学院，上海 200093)

基于PSO优化的车辆稳定性研究

陈宇奇，陈家琪

(上海理工大学 光电信息与计算机工程学院，上海 200093)

为了改善汽车行驶的稳定性，在基于模糊控制器控制的ESP系统基础上，运用粒子群算法对其进行优化，并运用Adams/Car和Matlab/Simulink在单移线、双移线工况下进行联合仿真，仿真结果证明，优化后的ESP系统解决了车辆系统模型非线性及参数的多变复杂性强等问题，并有效克服了模糊控制器存在的稳态偏差和极限环，提高了汽车行驶安全。

联合仿真；粒子群算法；模糊控制；ESP

汽车电子稳定系统(Electronic Stability Program，ESP)是在汽车自动防抱死系统(Antilock Brake System ABS)和汽车驱动防滑系统(Acceleration Slip Regulation，ASR)的基础上加以系统地控制，拥有对驱动力、制动力进行自动补偿和修正的综合控制能力。ESP通过控制车轮的制动力或发动机的输出力矩，来控制汽车的横摆角速度并将车辆的侧偏角限制在一定范围内，从而在进行高速急转弯、躲避前方突然出现障碍物以及低附湿滑路面等处于附着极限时，帮助驾驶员控制汽车的操纵稳定性[1-2]，防止车辆出现过度转向或转向不足等危险状况，提高驾驶安全。

本文针对某车型建立Adams和Matlab联合仿真系统模型，经粒子群优化的模糊控制器对质心侧偏角、横摆角速度的控制，并对控制结果进行仿真验证，探讨经过粒子群优化的汽车ESP系统的合理性及有效性。

1 ESP系统的组成及原理

电子稳定程序，简称ESP，包含ABS及ASR，是这两种系统功能上的延伸，其区别在于ABS及ASR只能被动地做出反应，而ESP则能够主动探测和分析车况，防止驾驶人员操作错误[3]。ESP工作的基本原理是利用汽车上的制动系统，在允许的范围内，通过控制汽车车轮制动器的工作，保持车辆在不同路况上的稳定行驶。电子稳定系统通过侧向加速度传感器识别车辆实际运动方向并通过横摆角速度传感器检测车辆旋转角度[4-5]，传送到ECU中与标准值进行对比，通过汽车发动机输出力矩和车轮制动力矩的调控对车身稳定进行控制。

2 车辆模型

2.1 整车模型

进行车辆操纵稳定性研究的基础是建立合适的车辆动力学模型。为提高建模效率和保证整车模型的精度，使其尽量接近实际的物理样机，本文选择在机械多体动力学软件Adams/Car中进行整车模型的建立[6]。建模后，为了保证其模型的准确性，通过单移线变道仿真和角阶跃转向仿真两种典型工况，验证车辆模型的有效性和正确性。

2.2 参考模型

本文选取二自由度线性车辆作为参考模型来计算其输出的各理想值。假设车辆的轮胎特性是线性的，且沿x轴的车速恒定，仅有y轴的侧向运动和z轴的横向运动两个方向的自由度[7]。建立线性二自由度整车参考模型的运动微分方程为

(1)

(2)

(3)

3 控制方法

3.1 模糊控制器

模糊控制理论不仅可解决诸多复杂而难以建立精确数学模型的对象或系统问题，也是处理时变和不确定性问题的一种有效方法，在汽车非线性系统中，运用模糊控制器能达到较好的效果。然而在模糊控制器的设计中，首要确定的是其维数和系统变量，然后利用输入输出变量的数目来确定控制器的结构。本文ESP控制器采用较为广泛的二维模糊控制结构，以车辆的质心侧偏角和横摆角速度作为目标控制变量，其输入分别是实际质心侧偏角、实际横摆角速度与理想质心侧偏角、理想横摆角速度的误差e及误差变化率ec，输出是附加的横摆力矩[8]。

3.2 粒子群算法

粒子群优化算法是Kennedy博士和Eberhart教授于1995年提出的并行的优化算法，其算法简单，不要求被优化函数具有可微、可导、连续等性质，收敛速度快。

基本的粒子群算法中，每个粒子代表一个可行的潜在解，所有的粒子组成群体。粒子在解空间中按照自身运动的历史信息和群体信息决定其接下来运动的速度和方向，以此找到最优解。

粒子群算法的邻域函数在每一个迭代周期通过个体速度向量、位置向量、个体运动历史状态、群体状态和扰动来产生新的位置信息，每维的速度与位置更新公式为[9]

vid+1=ω+vid+c1×rand(1)×(pid-xid)+

c2×rand(1)×(gid-xid)

(4)

xid+1=xid+vid+1

(5)

其中，c1和c2为正常数，称为学习因子；rand(·)为[0, 1]之间的随机数；ω称为惯性因子，能始终群扩展搜索空间，获得较好的求解效果，ω较大适于对解空间进行大范围探查，ω较小适于进行小范围探查。粒子群初始位置和速度随机产生，然后根据式(4)和式(5)进行迭代，直至找到最优的解。

3.3 粒子群优化模糊控制器

车辆系统模型非线性及参数的多变复杂性较强，无法建立精确的数学模型。因此，经典的控制方法如PID难以实现，为解决这一问题，需要设计鲁棒性与自适应性较强的控制器[10-11]。本文ESP控制器使用模糊控制算法实现对车身的稳定性控制，模糊控制无需建立被控对象的数学模型，利用人类专家的控制经验，对于非线性系统有很强的鲁棒性。由于模糊控制器的参数对模糊控制器的稳态性能影响较大，因此在参数选择不当时，系统容易产生稳态偏差和极限环，为了克服稳态偏差和极限环，在模糊控制的基础上加入积分环节是较好的方法。但在何时引入纯积分环节以及在什么位置引入积分环节则难以把握。因此本文利用PSO算法来优化模糊控制器的参数E、EC、U[12-14]。

4 联合仿真

4.1 仿真控制器设计

基于Matlab/Simulink和Admas软件环境，控制系统从Admas模型中读出横摆角速度、质心侧偏角，经过控制系统的计算后，得出横摆力矩的大小，输入到Admas车辆模型中，对整车进行控制，联合仿真输入输出结构如图1所示。

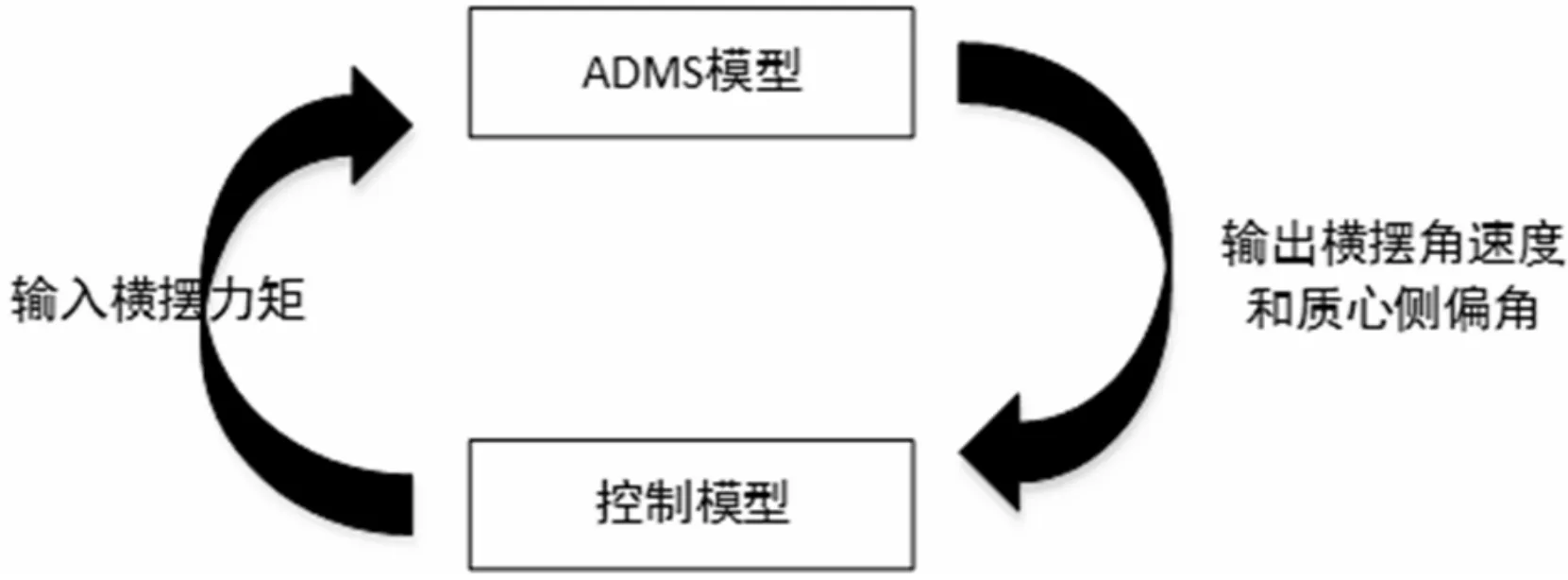
图1 联合仿真输入输出结构

将事先建立好的整车模型导入Simulink中，加入粒子群优化后的模糊控制器，即建立联合仿真控制系统的模型如图2所示。此模型中通过整车模型输出质心侧偏角、横摆角速度、车身速度、和方向盘的转角4个变量，其中车身速度和方向盘转角分别输入到参考模型中，得到参考模型中实际的质心侧偏角和横摆角速度，实际的质心侧偏角、横摆角速度和参考的质心侧偏角、横摆角速度产生误差和误差率作为输入变量输入到经粒子群优化过的模糊控制器中，输出横摆力矩及时反馈到整车模型中，通过控制4个车轮的横摆力矩，及时对驾驶员的操作进行纠正，较好地控制车身的稳定性。

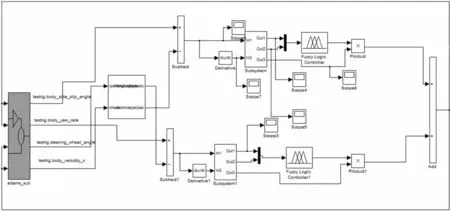
图2 联合仿真控制系统模型

4.2 仿真分析

(1)单移线仿真实验。

单移线工况仿真是指车辆在一定时间内，完成一个S型道路，来模拟车辆高速变道或紧急避障动作，在附着系数0.5的湿滑道路上，初始速度为150 km/h，前轮转向角输入为正弦输入，最大转向角为50°，转向开始时刻2 s，具体仿真结果如图3和图4所示。

图3 横摆角速度输出

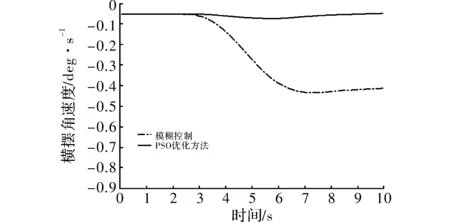
图4 质心侧偏角输出

横摆角速度输出曲线如图3所示和质心侧偏角输出曲线如图4所示。可以看出：模糊控制单独作用的车辆在2 s时，横摆角速度开始逐渐增大，在3 s时质心侧偏角开始逐渐增大，约在8 s趋于稳定。虽然最终车辆也可到达稳定，但时间较长且控制效果也并不理想，当发生转向不足或过度时，要依赖驾驶员的调整，若驾驶员反映迟钝则可能会发生交通事故。当加入经PSO优化模糊控制下，车辆的横摆角速度和质心侧偏角都得到了较好的控制，顺利实现了避障动作，具有良好的瞬态响应能力，显著的提高了车辆的操纵性。因此，在极限速度的工况下，经过PSO优化的模糊控制器比单一的模糊控制更能有效的降低车辆的横摆角速度与质心侧偏角，保证车辆的操纵稳定性。

(2)双移线仿真实验。

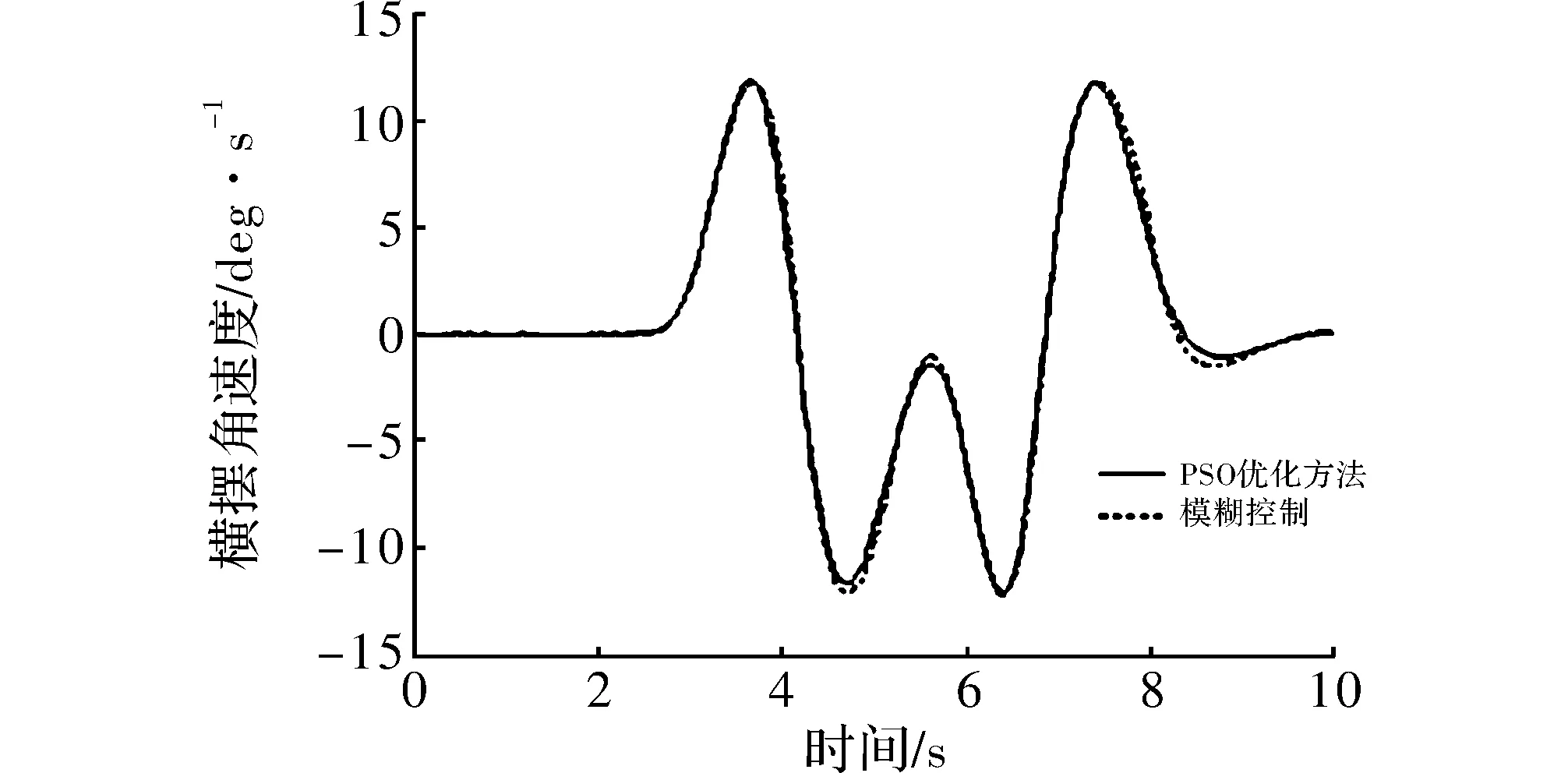
图5 横摆角速度输出

双移线工况仿真是研究车辆紧急避障和检测车辆操纵稳定性的重要实验，在附着系数0.5的道路上，初始速度为150 km/h，最大转向角为40°，转向开始时刻2 s。横摆角速度输出曲线如图7所示和质心侧偏角输出曲线如图8所示，只有模糊控制和经PSO优化的模糊控制作用的车辆在2 s时，横摆角速度开始逐渐增大，在3 s时质心侧偏角开始逐渐增大，但经过粒子群优化后的车辆的横摆角速度和质心侧偏角响应自整定速度加快，最大超调量幅值明显减小，动态控制效果得到改善，显著提高了车辆的操纵性。因此，在极限速度的工况下，经PSO优化的模糊控制和模糊控制都能使车量保持较好的稳定性，而前者的控制效果略优于后者。

图6 质心侧偏角输出

5 结束语

经过PSO算法优化的模糊控制器使汽车的横摆角速度和质心侧偏角得到了良好的改善，而且粒子群算法有求解速度快和鲁棒性强的特点，提高了汽车在高速急转向时的操纵稳定性能，和单一的模糊控制相比，能较好的控制车身的稳定性，增加驾驶员的操纵安全性。粒子群优化算法也存在一些不足，基本的粒子群算法易陷入局部最优，会影响优化效果，在PSO 算法上还有待改进。

[1] 严世榕,严钟辉.基于模糊PID的客车操纵稳定性控制研究[J].机械制造与自动化,2015,44(6):163-166.

[2] 李刚,王超,石晶,等.基于模糊控制的汽车直接横摆力矩研究[J].计算机仿真,2014,31(12): 151-155.

[3] 付燕荣,王国业,关志伟.汽车ABS/ASR/ESP集成控制策略研究[J].机械设计与制造工程,2014, 43(2):35-40.

[4] 李向瑜,高振海,郭建,等.汽车装备电子稳定性程序后的性能评价方法[J].拖拉机与农用运输车,2008,35(4):1-4.

[5] Bosch B. ESP system: 5 years of experience[C].Germany:Automotive Dynamics & Stability Conference,2012.

[6] 赵秋芳.基于ADAMS的汽车操纵稳定性仿真试验初步研究[D].大连:大连理工大学,2006.

[7] Koibuchi K,Yamamoto M,Fukada Y, et al. Vehicle stability control in limit cornering by active brake[J]. Jsae Review, 1995, 16(3):323-323.

[8] 王德平,郭孔辉.车辆动力学稳定性控制的仿真研究[J].汽车技术,1999(2):8-10.

[9] 李宁.粒子群优化算法的理论分析与应用研究[D].武汉:华中科技大学,2006.

[10] 孟庆宽,仇瑞承,张漫,等.基于改进粒子群优化模糊控制的农业车辆导航系统[J].农业机械学报,2015, 46(3):29-36.

[11] 韩璞,王学厚,李剑波,等.粒子群优化的模糊控制器设计[J].动力工程学报,2005,25(5):663-667.

[12] 祁春清,宋正强.基于粒子群优化模糊控制器永磁同步电机控制[J].中国电机工程学报,2006, 26(17):158-162.

[13] 郝万君,强文义,柴庆宣,等.基于粒子群优化的一类模糊控制器设计[J].控制与决策,2007,22(5):585-588.

[14] 姜柏庄.基于PSO算法优化的模糊PID异步电动机控制系统研究[D].湘潭:湖南科技大学,2014.

Research on the PSO to Optimize Vehicle Stability Study

CHEN Yuqi，CHEN Jiaqi

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 20009, China)

In order to improve vehicle stability, use PSO to optimize ESP system which based on fuzzy controller in this paper. Using Adams/Car and Matlab/Simulink to do co-simulation under the conditions of single-lane and double-lane. Simulation results show that the optimized ESP system could solve the vehicle system’s non-linear model and parameters varied highly complex issues.And effectively overcome the steady-state error of fuzzy controllers exist and limit cycles, improve safety cars.

co-simulation; PSO; fuzzy control; ESP

2016- 03- 21

陈宇奇(1991-)，男，硕士研究生。研究方向：控制算法。陈家琪(1957-)，男，教授。研究方向：计算机测控系统等。

10.16180/j.cnki.issn1007-7820.2017.01.023

TP391.9

A

1007-7820(2017)01-083-04