创设数学课堂有效情境的策略探讨

郑丹凤

摘 要：文章以教研活动为契机，立足于数学教学实际，以“勾股定理”一课为例，创设动手实践型的问题情境，发展学生动手能力；创设主动反思型问题情境，激发学生质疑精神；创设生活建模型问题情境，加深学生应用意识；创设类比迁移情境，培养学生类比思想；创设开放探究型问题情境，拓展学生发散思维。

关键词：中学数学；课堂教学；有效情境；互动；体验

中图分类号：G633.63 文献标志码：A 文章编号：1008-3561（2017）08-0030-01

一、背景介紹

本学期学校开展了以“疑难问题教学”为主题的校本教研活动，学校的黄老师开出了一节课“探索勾股定理”。在互相研讨的过程中，教师们发现创设有效的情境，可以调动学生学习的积极性，使学生更加主动地进行观察、猜测、实验、证明与应用，从而进行有效的数学学习。

二、案例描述与评析

黄老师的引入采用如下的情境：

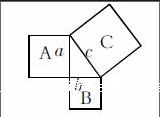
（1）采用几何画板让学生欣赏奇妙的勾股树，改变勾股树的层数，引导学生猜想最外层的小正方形面积之和与底下最大的正方形面积之间的关系。

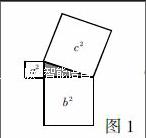
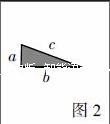
（2）更改勾股树的层数为1，引导学生探究勾股树的基本图形是否具备外层的两个小正方形面积之和与底下的大正方形面积相等的关系。第一，让学生观察左下图。问题1：三个正方形的面积之间有什么关系？问题2：用直角三角形的边长来表示对应的正方形面积。 问题3：直角三角形三条边的长度之间存在什么样的关系？第二，学生在格点图中发现这个特殊图形中两个小的正方形面积之和等于大正方形的面积，即：a2+b2=c2。猜想在一般情况下，是否所有的直角三角形都具备这样的性质。第三，在几何画板中实验：尝试改变直角三角形的形状：在几何画板软件中隐去方形网格，并保持直角不变，改变直角三角形的两条直角边长，通过测量和计算验证所有的直角三角形都具备这样的性质。第四，用面积法证明勾股定理：用勾股树基本图形中的两个小正方形和一个大正方形（图1），同时借助4个全等的直角三角形（图2），拼出了同一个正方形（图3），从而得出定理。第五，验证猜想的正确：由于勾股定理成立，从而得出在勾股树的基本图形中，两个小的正方形面积之和等于大正方形的面积。

（3）推论：不管勾股数的层数是多少，从外向内或者从内向外依此类推，最外围的所有正方形面积之和都等于底下最大的正方形面积，从而得出猜想是正确的。

三、关于案例的反思

从黄老师的这节课可以看出，由于创设了有效的问题情境，学生的学习积极性很高。如何才能创设有效的问题情境呢？

（1）创设动手实践型的问题情境，发展学生的动手能力。创设动手实践型的问题情境，学生可以在问题的解决过程中，自己动手动脑去制作、设计，这样既能发展学生的动手能力，也更加有助于他们发现规律。动手实践型的问题情境，可以让学生亲自动手实验，也可以借助软件平台进行模拟实验。比如在本案例中，黄老师在对勾股定理进行验证时使用了几何画板软件，在用面积法证明勾股定理时采用让学生动手拼一拼的方法，这样设计之后可以让学生主动参与探究问题，体验知识的形成过程，为建构新知识创造条件。

（2）创设主动反思型的问题情境，激发学生的质疑精神。创设主动质疑的问题情境，可以激发学生的质疑精神，从而产生对问题刨根问底的欲望，体会到学习的快乐。

（3）创设生活建模型的问题情境，加深学生的应用意识。创设生活应用型的问题情境，可以让学生体会数学学习的意义，使学生留下更深刻持久的印象。比如本案例中，若像课后某些老师提议的，可以设计一个生活问题情境，例如，在台风“麦莎”的袭击中，一棵大树在离地面9米处断裂，树的顶部落在离树根底部12米处。这棵树折断之前有多高？（篇幅所限，图略）

（4）创设类比迁移型的问题情境，培养学生的类比思想。中学数学中有许多概念、解题方法等具有相似的属性，可以采用类比的方式进行教学。比如学生在学解一元一次不等式时，就可以先回顾一元一次方程的解法，然后把方程中的等号改成不等号，引导学生得出解一元一次不等式的步骤，通过类比解一元一次不等式与一元一次方程的相同和不同之处，使学生把已有的知识转移到新知中去，使学生的知识和能力都得到了提升。

（5）创设开放探究型的问题情境，拓展学生的发散思维。创设开放探究型问题情境，并且由于它的条件不完备、答案不确定等原因，可以使不同的学生在同一问题上有不同的发展，从而让每个学生都有体验成功的机会，在成功的基础上探索更深层次的问题，拓展学生的发散思维。

参考文献：

[1]郑强.初中数学课堂教学的55个细节[M].成都：四川教育出版社，2006.

[2]韩倬.让思维之河自然地流淌——“勾股定理”的教学探索[J].中学数学教学参考，2010（07）.