一道初中数学题的探究式教学

■经桂兰

一道初中数学题的探究式教学

■经桂兰

随着新课程标准的实施，教师的教学理念、教学行为都在悄然变化，一些新的教学方式也应运而生。以“学生活动和问题研究”为中心，引导学生自主探究，挖掘学生创新潜能的探究式教学，倍受大家青睐。可在实际教学中，如何探究、探究的素材从何而来等问题又困扰着一线教师。在这里，笔者拟结合一道课本习题的探究式教学，谈几点个人体会。

一、教学实录

1.问题提出。

苏科版七年级《数学》（下）P42第20题：

（1）如图1，在△ABC中，∠ABC、∠ACB的平分线相交于点O，若∠A＝40°，求∠BOC的度数。

（2）如图2，△A′B′C′两个外角∠C′B′D′、∠B′C′E′的平分线相交于点O′，∠A′＝40°，求∠B′O′C′的度数。

（3）由（1）（2）可发现∠BOC与∠B′O′C′有怎样的数量关系？若∠A＝∠A′＝n°，∠BOC与∠B′O′C′是否还具有这样的关系？为什么？

本题从特殊到一般，由内而外，层层设计，并且解法多样，故有一定的解法探究和问题拓展延伸变化的空间。

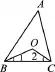
图1

图2

2.问题探究。

探究伊始，先解决前两个问题。

生1利用一般方法求出了∠BOC的度数，而生2则把问题（1）进行转化，用已解决的问题解决新问题，给课堂带来了生机和活力。在座的学生顿时有了精神，个个跃跃欲试，积极举手发言。

初步探究，解决问题（3）。

生3针对本题，得到了“∠BOC与∠B′O′C′互补”的结论。当∠A=∠A′=n°时，生4很快给出了一般问题的解法，让大家体会到了符号意识、从特殊到一般、类比的数学思想。这时，聪明好学的生5着急地举手，迫不及待地说，可将图1中的∠BOC平移到图2中，使B与B′重合，C与C′重合，从而得到∠BOC与∠B′O′C′互补。生5通过平移构造，把两个角集中在了一个图形中，从整体上进行研究，简捷明了，得到了同学们的称赞，同时，课堂也进入了高潮。

深入探究，将问题进行拓展延伸。刚才探究的角平分线同是内角的或同是外角的，让学生试着给出一个不同情形的问题，可小组合作交流。

生6给出了一个关于三角形的内角平分线和外角平分线的夹角的题目：

如图3，在△A′′B′′C′′中，∠A′′=n°，内角∠A′′B′′C′′的平分线与外角∠A′′C′′F的平分线相交于点O′′，∠B′′O′′C′′与∠BOC、∠B′O′C′有怎样的数量关系？

图3

这个问题编得很好，条件、问题说得很清楚，也很全面。生9和生10又运用了生5的构造方法给出了这道题的精彩解法。这种学生之间的互相学习、共同发展，正反映了数学教学是数学活动的教学，是师生之间、学生之间交往互动与共同发展的过程。

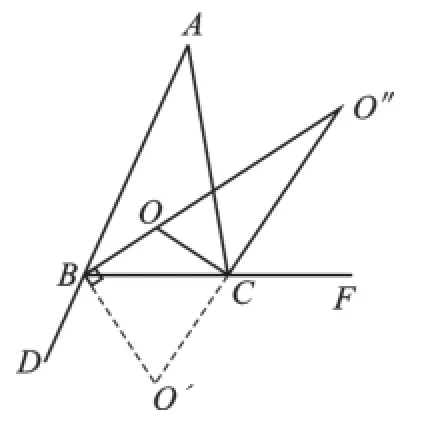
图4

最后，我对这堂课进行了总结，画出了图4，并给出了相应结论。面对总结，学生们表现出极大的兴奋，有些同学甚至说，看似复杂的问题，其实就这么简单。

二、教学反思

回顾本节课，学生的表现，可谓精彩连连。生2出其不意的转化法，初露风采，拉开了探究的序幕；生5突发奇想的平移构造法，精彩至极，把探究直接推向高潮；生6深思熟虑的问题演变，生9、生10学以致用的新平移构造法，让整个课堂始终处于学习气氛之中，学生的探究热情一浪高过一浪。

这次教学，不仅达到了“解一题，会一类，通一片”的效果，而且让学生在问题的探究过程中，体会了从特殊到一般、类比、转化、整体、构造等数学思想方法，积累了观察、操作、思考、探索、合作、交流等活动经验，培养了创新精神，激发了学生的学习热情。反思精彩，让我对习题探究式教学有了更深的认识和体会。

1.探究的素材源自平常的问题。

在日常教学中，我们有些教师苦于没有探究素材，不知探究的素材从何而来。其实，课本中的习题就是丰富的素材。

习题本身就是问题，而围绕这个问题拓展、延伸与变化，就是一类问题。在拓展、延伸或变化中，对问题可进行“一题多解”，又可进行解法探究。本节课正是针对课本中的一道习题，从问题的演变和解法两个方面进行探究。其教学效果超乎想象，是教师讲授灌输所无法企及的。

在实际教学中，我们可结合学生习题，从中选取一些有拓展、延伸空间或解法多样的题目，重点讲评，重点探究，切实提高习题教学的有效性。

2.有效的探究离不开精心的预设。

时常听到教师们的这些声音：生源差，学生不会探究，与其让学生探究花时间，还不如直接讲授。当然，探究式教学不是万能模式，提倡而不能滥用。在日常的教学中，教学方式的使用应视具体的学情、教学内容、教师的能力等情况而有所选择。但无论是哪一种教学方式的使用，教师都应做好精心的预设。

在本课中，精彩不仅来自于生5这样聪明学生的给力表现，也来自于教师事先就设计好的问题拓展、解法探究等活动。若没有出现生5的解法，教学该怎么进行呢？这就要求我们教师首先会这种解法，并做好相应预设。教学中，可采取延迟探究，即先对问题做拓展延伸，看初步探究阶段中是否有学生给出构造法。如果仍然没有，我们教师可做适当启发、引导。比如，启发学生：我们要讨论的∠BOC与∠B'O'C'，在两个图形中，能否将它们集中起来？给学生以适当的启发，引导学生探究，也能明确探究方向，在有限的课堂时间内做有效的探究。

总之，问题探究不在于问题的难易、多少，而在于教师对问题的内涵与外延的研究、把握和使用。精彩探究也不在于学生的素质、能力，全在于课前教师精心的预设、课堂上教师有效的引导和长期的坚持。

(作者为江苏省南京市溧水区高级中学附属初中教师)