激活思考?创新方法

张贺

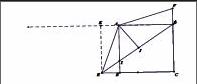
在学习解直角三角形时做了一节习题课，孩子们对网格图中的角转化产生兴趣，明确构建直角三角形的方法，他们觉得有格点可依，便于发现，有利于转化角。但是对于求解三角函数的问题：在正方形ABCD中，BC=3，点E，F分别是CB，CD延长线上的点，DF=BE，连接AE，AF，过点A作AH⊥ED于点H .

（1）求证：△ADF≌△ABD

（2）若PE=1，求tan∠AED

针对该题学生有思考方向，当学生初识此题，思路单一，方向明确要将∠AED构建在直角三角形中，即使构建出直角三角形但也無法求解三角形，甚至觉得该题难度很大。尤其是（2）当时能有思路的同学占总人数的85﹪，进行准确计算的只剩下不足15﹪。经历一段时间后，孩子们的思考经过沉淀，为了激活学生的思考模式，在课堂上采取研讨交流式学习模式，自主讲解组内

突破。

“这道题至少有两种方法，请大家在小组内展示自己的想法，看哪个组率先有方案并能及时展示。”教师的引领下，各小组马上投入交流环节。班级整体交流后展现了以下方法：

1.过点A作AJ⊥DE 垂足为J，在Rt△ADJ和Rt△AEJ中由勾股定理得：AD2-DJ2=AE2-EJ2即：32-（5-EJ）2=（）2-EJ2，解得EJ，再利用勾股定理求解AJ，从而解决tan∠AED.

2.设DE，AB的交点为I，观察△BEI和△ADI的关系，利用相似型求DI，AI ，利用三角形的面积 即：AI*AD=DI*AJ求出AJ从而解决tan∠AED.

3.观察△ADE，过点E作EK⊥DE，垂足为K，该三角形的面积可以利用AD*EK=DE*AJ来解决，因为AD=3，EK=AB=3，DE=5，所以AJ可求，再利用勾股定理解决EJ，即能解决tan∠AED。

4.在该图形中因为Rt△EDC是已知三角形，所以tan∠DEC=3/4，因为∠ADE=∠DEC，所以tan∠DEC= tan∠ADE=3/4Rt△ADJ中已知AD，我们可解△ADJ中的边AJ，DJ，进而得EJ，即能解决tan∠AED。

学生的思维进行了有力的碰撞，激起思维的火花，在热情的交流过程中，即提高了对问题的认知程度，又能锻炼孩子们的语言表达能力，组织能力，在争论中让孩子们相互合作互相有新的认识提升了解程度。师者的引领和及时点拨，给孩子们信心，为问题的提升知识点的应用起到画龙点睛的作用。