初中数学课堂“二次函数”教学的优化策略

胡小茂

[摘 要] 初中生学好二次函数有着非常重要的意义，本文联系实践，探讨了初中数学课堂优化“二次函数”教学的相关策略.

[关键词] 初中数学；二次函数；教学策略；优化策略

“二次函数”是初中数学中最重要的基础知识之一，其对应的知识和方法在生活中有着广泛的应用，更是进行高中阶段数学学习的基础. 因此，初中生学好二次函数有着非常重要的意义. 实际教学中，初中教师应该如何帮助学生学好相应的内容呢？下面，笔者结合教学实践谈谈自己的思考，以供读者参详.

关注概念教学，注重学生知识

的生成过程

数学概念是数学知识框架的基础，二次函数也不例外，教学中二次函数的概念学习对学生理解函数图像与性质，以及对二次函数的应用都有着直接的影响. 现实教学中，教师往往表现得急功近利，即直接讲授二次函数的形式与定义，然后匆匆进入习题讲练，以练习来替代理解. 这样学生只能在直观上对二次函数产生肤浅的认识，而不能从根本上进行理解，更无法深刻体会其实质以及相关数学思想. 而且，如果教师脱离学生的认知基础来灌输二次函数的概念，那么学生的认知将缺乏大量的生活实例作为其理论支撑，这样的处理将导致二次函数无法纳入学生的认知体系，这无助于学生知识系统化的构建.

二次函数概念的学习应该是一个系统的过程，即该过程应该通过以下四个方面的有机整合.

1. 概括

学生对二次函数的概念学习需要结合具体的实例，比如正方形的面积与其边长的关系、多边形的对角线条数与其边数之间的关系、周长确定的矩形面积与其长的关系等，充分依托学生已有的函数基础来引导学生自己写出函数表达式，进而从形式上发现其自变量的最高次项为二次，则二次函数的引入将水到渠成.

2. 表述

根据二次函数的关键性特征，并与学生之前所学的函数类型进行充分对比，由此引导学生自发表述二次函数的概念，即形式上类似于y=ax2+bx+c（a，b，c三项为常数，且a不等于0）的函数为二次函数. 同时鼓励学生讨论a，b，c三项如果分别取0，则可能对函数带来怎样的影响，由此引导学生深入理解二次函数的概念.

3. 识别

完成有关二次函数的概念概括和表述之后，教师应该帮助学生检测自己的理解程度. 可以提供一系列函数表达式给学生，让他们结合其关键特征进行判断，在检测的同时也进一步拓展学生的眼界.

4. 运用

即为学生提供更加复杂的函数形式，让他们结合概念进行判断，也可以创设一些数学情境，让学生自己分析哪些情境下可能会产生二次函数，由此提升学生的建模能力和数学思维.

提升数学教师的专业素养，实

现教学观念的转变

教学中我们也有这样的发现，初中生之所以在二次函数的学习中存在困难，有部分原因是源自于教师. 教师在教学中的讲解模棱两可，抑或是出现错误，再加上无法通过现代教育技术手段来促进学生的理解，这些都将导致学生二次函数学习的困难. 教书育人是教师的天职，教师要在自己的工作中帮助学生习得知识，获得发展. 面对学生在二次函数学习过程中所显露出的困难，教师要积极提升自己的水平，深入钻研数学教育理论，更加充分地进行备课，并积极探索信息技术、多媒体技术等现代化教学手段的使用方法，以进一步优化课堂、提升效率.

初中数学是学生发展的根基所在，无论将来學生是进入高中继续深造，抑或是走向社会，数学都是必备知识. 因此学生的初中数学学习都应该建立在知识正确的前提下，这就要求教师在教学中不能含糊其辞，应该充分关注知识的严谨性和科学性. 比如二次函数的对称轴就一定要明确该对称轴是直线；以及初中阶段涉及的运用二次函数解决实际问题，不能让学生直接将函数形式转化为顶点式寻找顶点以及结合a取值的正负来探求最值，因为实际问题还涉及函数定义域的内容. 因此教学过程中一定要明确相关问题，注重知识的严谨性.

在课堂上，教师不仅要正确地传授知识，也要积极提升课堂教学效果. 比如在引导学生探索二次函数的图像和性质时，传统的做法是在黑板上画出几个具体的二次函数图像，然后通过对函数图像异同点的比较，总结出相应的函数性质. 事实上，有限的时间所绘制函数图像的个数是有限的，这样以点概面的教学所形成的认识稍有牵强，甚至有让学生进行死记硬背的趋势，对学生的数学思维造成了很大的限制.

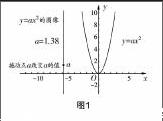
而以信息技术为代表的现代教育手段正在悄悄改变着我们的教学，借助多媒体，我们可以将抽象的数学概念以更加感性的形象呈现给学生，从而帮助学生有效建构认知. 在引导学生探索二次函数的图像及其性质时，教师可以预先运用几何画板画出y=ax2（a≠0）的函数图像，并通过调整a的取值来实现函数图像的动态变化.

如图1所示，通过调整点a可以改变a的具体取值，实现图像的变化. 学生由此可以比较a>0时，函数的相同处与不同处，进而引导学生归纳出对应情形下函数图像的性质. 在此基础上，教师让学生自己探索a<0时，函数图像的变化特点，由此也实现相关性质的总结. 此外，教师还可以类似地引导学生对二次函数y=ax2+k（a≠0）和y=a（x-h）2（a≠0）的图像进行研究，让学生从动态的场景来领会函数图像的变化，由此深刻体会平移的本质，进而掌握图像平移规律. 这不仅能提升学习效率，也能有效降低教师的劳动负荷，让抽象而生涩的数学课堂变得具体而生动.

注重学生学习习惯培养，让其

由“学会”走向“会学”

初中阶段的各门功课中，数学的难度是最大的，也是学生最容易丧失学习兴趣的，他们在遇到抽象问题时，很容易表现出信心不足. 所以积极的情绪状态是数学学习的关键，为此，教师要探索如何让学生由“学会”走向“会学”，并且由此发展为“乐学”.

二次函数体系庞大，包括概念、图像和性质的理解以及应用，整个学习也是一个由浅入深的过程. 学生在初始阶段还是充满兴趣的，但是随着学习的深入，内容越来越抽象，问题越来越难，兴趣也就逐渐消退，如何强化并延续学生的兴趣呢？其关键在于教师要善于发掘教学内容中的趣味元素，将数学史料、数学故事、数学趣闻融入课堂，为枯燥的课堂点缀上亮丽的色彩，这将有助于学生学习兴趣的延续、学习积极性的提高. 此外，教师注重学生主体地位的激发，通过积极的师生互动来带动课堂的氛围，也是激发学生兴趣的手段.

同时，教师在教学中要对学生进行恰当地评价，肯定表现优异的学生，鼓励学习困难的学生，对学习态度存在问题的学生要予以关注和纠正. 客观的评价能让学生明白自己努力的方向是否正确，有助于学习方式的纠正，也有助于他们继续在努力中获得成长.

强化二次函数的综合训练，培

养学生的问题解决能力

二次函数的最大难点还在于其综合性较强，受限于初中生的思维特点和能力发展水平，他们在初次接触二次函数问题时，或多或少在问题处理方面存在一定的问题. 七年级和八年级的数学学习中，学生的数学思维和能力的培养还是极其有限的，因此在九年级开始学习二次函数时，相关矛盾就暴露出来了. 因为二次函数强调数学建模处理，强调数形结合的数学思想，突出对学生创新意识和综合能力的考查，所以学生开始接触时，难免遇到障碍. 这就需要教师予以针对性的指导. 例如围绕动点情形来研究动线段的长度、动三角形的面积，这里就要求教师能够指导学生从具体情境中提炼二次函数的模型，然后再实现问题的解决. 教学实践中我们还发现这样的情况，学生处理二次函数实际问题时，常常审题不清，无法找到等量关系. 这既可以说是建模能力的缺失，也可以说是知识迁移能力的不足. 在此，教师要启发学生联系之前运用方程处理实际问题所采用的思路，仔细阅读问题的情境，提炼其中的数量关系，先写出相应的方程，再以函数思想进行分析和处理，这样将有助于问题的解决.

综上所述，虽然二次函数的教学存在一定的难度，但是只要能够从学生的认知基础出发，按照学生的认知规律，积极转换自己的教学理念，我们就能有效帮助学生克服困难，提升教学质量.