在数学语言转换中深化概念的理解

陆建峰

[摘 要]学习数学知识的过程就是数学语言转换、内化和运用的过程。数学语言包括文字语言、符号语言和图表语言，这三种语言形式各不相同，但在突出数学对象本质特征方面目标一致。在概念教学中，教师可以引导学生在概念形成的不同阶段灵活转换数学语言，促进学生深化理解数学概念。

[关键词]数学语言；转换；概念；分数

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）08-0039-02

数学教学也就是数学语言的教学。小学生学习数学知识的过程就是他们把数学语言进行转换、内化和运用的过程。在概念教学过程中，教师可以引导学生在概念形成的不同阶段灵活转换数学语言，促进学生提高语言转换的能力和表达能力，提升他们的数学素养。

一、在文字语言转换为符号语言中引入概念

概念引入是学生感知概念的初始阶段。引入新概念时，教师要用它的前概念帮助学生进行知识迁移。分数是小学数学的核心概念，它的前概念是除法的意义，根据小学生以形象思维为主的特点，教师要充分利用直观化手段，借助直观模型（如面积模型、数线模型等），让学生感知如何表示一个物体平均分成2份的结果，体会分数表示的是部分与整体的关系。“平均分”是分数产生的根源，表示“一半”的大小是分数产生的内需。引入概念时，教师用文字语言“一半”引导学生操作，让学生充分体会分数产生的必要性。

课始，教师先抓住文字语言“一半”在操作中的含义，创设小明想把所带物品（有8个奶片、4瓶牛奶、1块比萨饼、1张正方形彩纸）分“一半”给小红的现实情境，引导学生分出它们的“一半”。

学生用动作诠释了“一半”的含义——把物品平均分成2份，其中的一份就是它们的“一半”。学生在操作过程中初步感知分数既可以表示多个物品的一半（ 8个奶片的一半是4个，反过来4个奶片是8个奶片的一半），也可以是一个物品的一半。紧接着，一个物体的“一半”的大小如何用一个新的数表示呢？有的学生用[2][1][1] （2分成1和1）表示；有的学生用2|1表示；有的学生用表示；有的学生用表示……学生思维角度不同，反映了分数既可以作为过程性操作的分数（把“1”看作 “2”，平均分成2份，每份都是1），也可以作为一个结果的分数2|1、、。分数作为结果，表征形式上不同，但意义一致——都是把一个物体平均分成2份，表示其中的1份，把“关系”意义作为认识分数的逻辑起点，避免学生形成个（量）等同于（比率）的“糊涂”认识。把文字语言表达的“一半”借助动作表征转换为符号语言“”，能有效帮助学生实现概念感知阶段的初步抽象。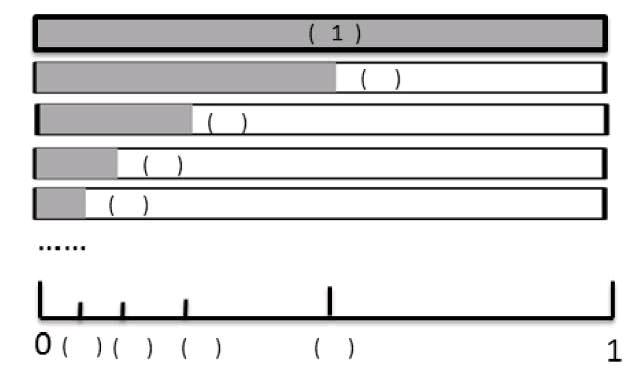

二、在符号语言转换为图表语言中形成概念

概念形成阶段是学生的学习重点，也是学生思维过程中最复杂的部分。概念形成不但要学生从许多事物和情境中抽象并概括出它们的共同特征，而且需要学生能辨別与概念不相关的非本质特征。学生在抽象概括的过程中，需要把符号语言转换成图表语言，借助于图形语言的直观性凸显概念的本质特征。

认识的意义时，教师先提出问题：“谁还能想到什么物体的‘一半？”引导学生先在头脑中建立具象，再提供各种材料（图形、实物）让学生选择，然后带领学生建构“”的现实意义：有的学生选择“切”出实物的“一半”；有的学生选择用图形“对折”出“一半”；有的学生选择在纸上“画”出“一半”……尽管方法不同，但学生在语言转换过程中都反映了“一半”的本质——把一个物体平均分成2份，其中的1份就是它的。接下来，让学生尝试“用图形说话”，结合图形与操作过程解释“”的实际意义，说出其中的“2”表示什么，“1”表示什么，“为什么折法不同，每一部分的形状也不同，但结果都可以用‘表示？”“为什么所选材料不同，创造的方式也不同，但都可以创造出？”最后，教师拿出一个胡萝卜，并将其从中间一分为二，问学生“是否每份都可以用表示”，突出平均分物体的大小所指向的模型意义，有助于学生在反思中识别分数意义的本质特征。

学生在实物操作中的“切”“折”“画”等过程就是把符号语言“”转换成图形语言的过程。这种转换，不但符合学生思维直观性的特征，而且有利于学生理解和掌握分数的意义。通过动作表征，学生能真正找出分数的图示意义；及时追问和引导，有利于学生在反思中把握知识本质；适时应用图形语言进行反例矫正，有助于学生澄清在概念形成过程中可能出现的混淆；非概念图形语言与概念图形语言的比较，有助于凸现概念的本质属性——分数与所分材料和形式无关，但和平均分的份数有关。

三、在图表语言转换为符号语言中深化概念

概念深化是指从已获得的概念中能够联想出与之有联系的新概念，可以是表征形式上的联系，也可以是操作方法上的联系，还可以是本质意义上的联系。分数对小学生而言是学习中的难点：一方面因为分数在生活中应用非常少，学生缺少相关生活经验；另一方面是因为整数运算是数“1”的累加（减），数的组成规则是“满十进一”，而分数由于“平均分”的份数不同，计数单位也不同，学生无法把整数计数规则顺利迁移到分数认识中，造成认知困难。因此，教师要有的放矢地引导学生把图表语言转换为符号语言，使学生体会分数概念的另一层意义——把一个物体平均分成n份，其中的每一份用分数表示就是。

教师首先引导学生自主创造分数。有的学生对折一条毛线创造出，有的学生将长方形纸对折两次，创造了它的，也有的学生选择圆形纸片创造出它的……不同分数的产生，帮助学生初步内化了分数与平均分成的份数之间的关系。教师应重点引导学生体会把1个物体平均分以后，表示其中每一份的数都比1小、比0大。在此基础上，当学生说出一个分数后，教师随即从图上找出对应的分母和分子，帮助学生认识分母表示平均分的份数，分子表示其中的一份，分数整体表示平均分成的份数与其中一份之间的关系。最后，教师出示一组图形（如下图），要求学生用分数表示涂色的部分。

学生通过创造分数，从认识“”的过程获得操作的方法和表征形式的经验，从而培养了自身的创造力和想象力。把直条图变成一条线段，并在线段上标出对应位置的分数的过程就是把图表语言转换为符号语言的过程。学生从认识直条图中的“1”开始，依次认识更多的分数，直观感知每个分数与整体的关系——把直条图“1”平均分成2份，每份是；把平均分成2份相当于把整体平均分成4份……以此类推，学生能逐渐掌握分数之间的大小关系：直条图变成一条线段，线段上每个点都可以对应一个分数，一直平分下去，直至趋近0……用图形语言解释符号语言，能使抽象符号语言变得直观、具体，有助于培养学生对分数的“量”感，促进学生对分数的整体认识，让学生更深刻地理解分数概念的本质意义。

总之，教师要遵循概念理解的层次性，合理使用各种数学语言，使学生在概念形成的过程中顺利构造知识网，从而理清知识的本质。

（责编 童 夏）