用数形结合法巧解“牛吃草”问题

王江平

[摘 要]数形结合既是一个重要的数学思想，又是一种常用的教学方法，在教学中渗透数形结合的思想，可以把抽象的数学概念直观化，可以使算式形象化，可以将复杂问题简单化。教学“牛吃草”问题中，教师只要恰当运用数形结合法，就可以把这类问题化难为易。

[关键词]数形结合；牛吃草问题；化难为易

[中图分类号] G623.5 [文獻标识码] A [文章编号] 1007-9068（2017）08-0081-01

例题1：一片草地每天都在均匀地生长青草，如果供15头牛吃，可以吃8周；如果供16头牛吃，可以吃6周。那么现在要供18头牛吃，可以吃几周？（假设每头牛每周的吃草量相同）

做这类题目，一般要按照以下四个步骤进行解答。

第一步：求出这片草地每周的长草量。

先把每头牛每周的吃草量具体化，设1头牛1周吃的草为1份，则15头牛1周吃的草为15份，15头牛8周吃的草为15×8=120（份）；16头牛1周吃的草为16份，16头牛6周吃的草为16×6=96（份）。可以做出如下线段示意图（如图1）。

120份可以看作是草地上原有的草与8周内新长出来的草；96份可以看作是草地上原有的草与6周内新长出来的草，通过图1学生很容易理解每周的长草量是（120-96）÷（8-6）=12（份）。这时，教师可以引导学生思考：“如果草地上的草每天都在均匀地生长，1头牛不停地吃下去，会不会有一天草地上无草可吃了呢？如果是10头牛、12头牛的情况又会怎样？13头牛呢？”此处也可以用入不敷出、积少成多举例说明，加深学生对每周的长草量的理解。

第二步：求出这片草地的原有草量。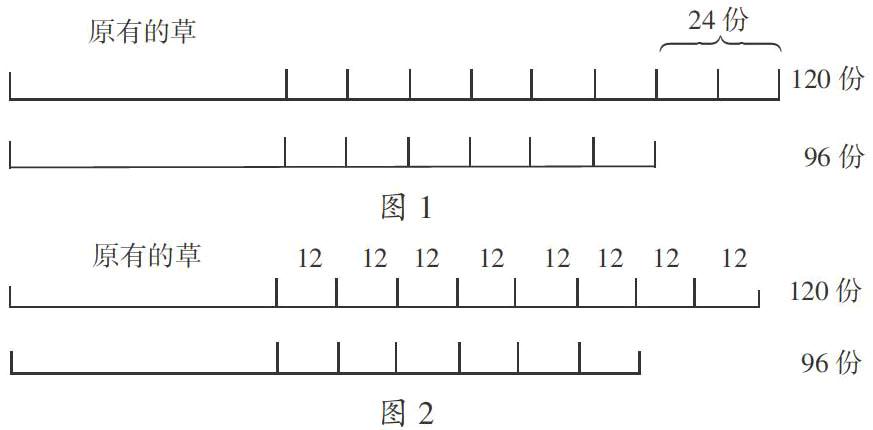

再看线段示意图（如图2）。120份减去8周内新长的草就是原有的草，即120-8×12=24（份），或者用96减去6周内新长的草也是原有的草，即96-12×6=24（份）。

第三步：求出每周实际消耗的原有草量。

对于这个问题，很多书上都是把牛分成两部分，让其中12头吃新长出的草，其余的牛吃原有的草来研究的，多数学生对这种方法在理解上有局限性，甚至有学生提出“让12头牛吃新长出的草，它不吃怎么办？”的问题。这时，教师可以换一种方式引导：18头牛1周吃的草是18份，而1周内新长的草是12份，那么新长的草够不够18头牛吃1周？如果新长的草不够吃，这些牛就要吃草地上原有的草，那草地上原有的草1周减少了多少份？列出算式就是18-12=6（份）。

第四步：求出牛可吃的周数。

这片草地原有的草为24份，每周减少6份，则可以吃24÷6=4（周）。

下面我们再来看看“牛吃草”问题在现实生活中的广泛应用。下列题目都是“牛吃草”问题的变式，解法也基本一样，所以就不再详解，略作说明即可。

例题2：一个水池装有一个进水管和三个同样的出水管。先打开进水管，等水池存了一些水后，再打开出水管。如果同时打开两个出水管，那么8分钟后水池排空；如果同时打开三个出水管，那么4分钟后水池排空。问出水管比进水管晚开多少分钟？

这道题虽然表面上没有“牛吃草”，但因为总的水量在均匀变化，“水”相当于“草”，进水管进的水相当于“新长出的草”，出水管排的水相当于“牛在吃草”，所以也是“牛吃草”问题。

例题3：某车站在检票前若干分钟就开始排队，每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失，同时开4个检票口需30分钟，同时开5个检票口需20分钟，如果同时开7个检票口，则需多少分钟？

这道题中，等候检票的旅客人数在变化，“旅客”相当于“草”，“检票口”相当于“牛”，每分钟来的旅客人数相当于“新长出的草”，开始检票前到的人数相当于“原有的草”，因此该题也可以用“牛吃草”问题的解法来解。

类似这些生活中常常遇到的水管排水、检票口检票、超市排队付款、水库泄洪、小船漏水淘水等问题，虽然从字面上看不一样，但问题的实质都是一样的，都属于“牛吃草”问题，都可以采用数形结合的方法解题。

综上所述，这种先画线段图，再利用数形之间的关系解答“牛吃草”问题的方法，有利于教师的教，有利于学生的学。学生在解疑答难的过程中，知识建构得既生动又深刻，不仅体会到了数学之美，还感受到了数形结合的魅力。对教师来说，教得轻松，教得自然，渗透着教师高超的教学智慧。教师要灵活运用数形结合思想，让数形结合思想走进学生的心灵，使绝大多数学生望而却步的“牛吃草”问题不再成为“问题”。

（责编 李琪琦）