让图像简化教学

摘要：在初中数学函数教学中，应用图像是一种很重要的教学方式，也是初中数学教学中的难点之一，因此探究初中数学函数的图像应用是非常有必要的.教师要认识到图像教学在初中数学函数教学中的重要性，并采取有效的方法，运用图像来简化数学教学.

关键词：初中数学；函数；图像分析

作者简介：姚永华（1978-），男，江苏江都，本科，中学一级教师，主要从事初中数学教学研究.在初中数学函数教学中，应用图像是一种很重要的教学方式，也是初中数学教学中的难点之一，因此探究初中数学函数的图像应用是非常有必要的.在图像教学中，教师把数学函数与图像相结合，有利于吸引学生的学习兴趣，发挥学生的主观能动性，同时，数形结合的教学方式能够加深学生对于数学函数的理解.更重要的是，学生在利用图像分析函数时，能够充分利用自己的智慧，有利于学生创新能力的培养和动手画图能力的提高.因此，教师要认识到图像教学在初中数学函数教学中的重要性，并采取有效的方法，运用图像来简化数学教学.本文针对初中数学函数的图像应用提出一些策略.

一、了解基本知识点

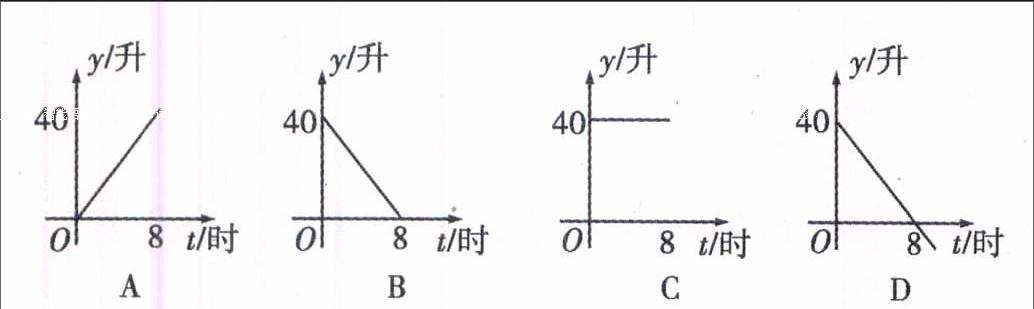
函数的应用范围很广泛，涉及到生活的很多方面.同时， 函数教学不仅是初中数学教学重点，也是中考的重点.可见，教师在初中教学中对函数教学要有很高的重视程度和科学的教学方式.同时，教师如果想让学生能够熟练地掌握并应用图像解决函数问题，必然要先让学生对函数图像的基本知识点有一个深刻地认识.首先，教师要把一次函数及其图像的基本要素介绍给学生：一次函数的基本形式为y=kx+b（k、b均为常数，k≠0）；一次函数的图像为直线形式；直线的倾斜程度表示直线斜率及k值的大小等.同时，在开始学习描绘图像时，教师要让学生遵循：列表、描线、连线的步骤，了解图像各点所代表的意义，学生熟练之后，可根据图像上的两点直接连线画出图像.例如：一辆汽车在开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量y（升）与行驶时间t（时）的函数关系用图像表示应为下图中的（D）.

本题与生活实际紧密相关，看似比较麻烦.学生要学会分析数学模型，选择与解题相关的叙述，就会简单很多.本题主要考查学生对实际生活中相关问题的一次函数的确定，及对函数图像的基本特点的了解.本题的一次函数关系式为：y=-5t+40，-5即为本题的斜率k值，40即为图像与y轴的交点.学生通过简单的函数和图像的分析即可确定答案.同样，教师也要把二次函数及其图像的基本要素介绍给学生.如：二次函数的基本形式为：y=ax2+bx+c（a≠0）；二次函数的图像为一条曲线；图像的对称轴方程为：x=-b2a；及根据a的正负不同，在对称轴两侧，y随x的变化而变化的情况.学生对这些基础知识有了深刻的理解，才能在以后的函数问题解题中更熟练的应用图像解决问题.

二、传授解题方法

为了让学生在做题过程中能够更快更准确地写出答案，教师要将常考的考点，及一些常用的解题方法教授给学生.首先，教师要让学生学会分析图像中一些特定的点所蕴含的解题信息；让学生注意数形结合，将函数及图像中的信息相结合；注意一次、二次函数的结合及转化.其次，教师要让学生学会用待定系数法求解函数方程，用数形结合的方法分析图像和函数之间的关系.

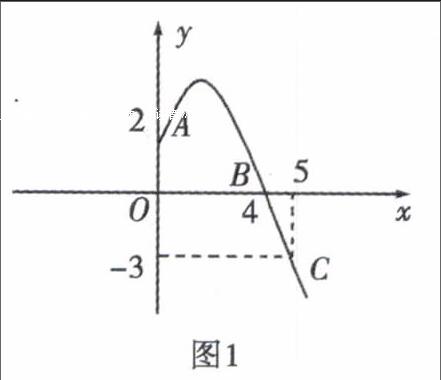
例如已知抛物线y=ax2+bx+c经过A，B，C三点，当x≥0时，其图像如图1所示，求抛物线的解析式，并写出顶点坐标.

解析设所求抛物线的解析式为y=ax2+bx+c（a≠0）

由图像可知A，B，C的坐标分别为（0，2），（4，0），（5，-3）

∵c=2

16a+4b+c=0

25a+5b+c=-3解得a=-12

b=32

c=2

∴抛物线的解析式为y=-12x2+32x+2

y=-12（x-32）2+258

∴该抛物线的顶点坐标为（32，258）

这道题的特点是题中没有直接给出所求抛物线经过的点的坐标，需要学生从图像中观察得出，很好地锻炼了学生从图像中获取有用信息的能力及数形结合的意识.也让学生学会用待定系数法求解二次函数方程，及变换方程的形式：一般式、顶点式等.教师让学生熟练地掌握解题方法，能够帮助学生更好地运用图像这一解题工具，快速答题.同时，在运用图像解决问题时，也能锻炼学生的想象能力和创新能力，有利于促进学生的素质发展.

三、分析典型例题

教师让学生了解了函数的基本知识及解题方法之后，还有一项重要工作，就是与学生一起分析典型例题，让学生更深刻地体会到函数中的典型问题，熟练掌握常考的要点及其常用解题方法.同时，当学生对于函数图像有了一定的了解后，教师可以适当讲解一些较难的函数图像题目，让学生进一步加深对图像的理解.

例如如图2所示，抛物线y=-x2+2x+c与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连接BE交MN于点F，已知点A的坐標为（-1，0），则（1）求该抛物线的解析式及顶点M的坐标；（2）求三角形EMF与BNF的面积之比.

解析（1）∵点A在抛物线y=-x2+2x+c上

∴-（-1）2+2x（-1）+c=0，解得：c=3

∴抛物线的解析式为y=-x2+2x+3

∵y=-x2+2x+3=-（x-1）2+4，

抛物线的顶点M（1，4）

（2）∵A（-1，0），抛物线的对称轴为直线x=1，

∴点B（3，0），EM=1，BN=2

∵EM//BN

∴△EMF与△BNF相似

∴△EMF与△BNF的面积之比为（EMNB）2，

∴三角形EMF与BNF的面积之比14.

本题中出现了抛物线与x轴的交点问题；二次函数的性质；待定系数法的应用；曲线上点的坐标与方程的关系；相似三角形的判定和性质等考点，考察的方面比较综合，可以使学生更加熟练地掌握和运用图像解决问题.

总之，利用图像简化教学是初中数学函数教学中的必然趋势.教师要认清图像教学的发展方向，并且注重图像教学.同时，教师可以采取让学生了解函数和图像的基本知识、传授解题方法、分析典型例题等方式，将图像教学应用到初中函数教学中，加强学生用图像解题的能力，同时，利用图像简化函数教学，提升学生的成绩，提高教师的教学质量.同时，教师在利用图像教学的过程中，也可以培养学生的创新能力，促进学生的全面发展.

参考文献：

[1]王正美.初中数学中“二次函数”的教学策略研究[J].学周刊.2014（22）

[2]赵静.思维导图工具在教学分析中的应用[J].内蒙古师范大学学报（教育科学版）.2013（09）

[3]刘世华.如何提高数学课堂的教学效果[N].伊犁日报（汉）.2011

[4]郑志贵.浅谈初中二次函数的解析式及教学注意事项[A].中华教育理论与实践科研论文成果选编（第三卷）[C].2012