光谱、能级和能级图的理解和应用

■河南省三门峡市外国语高中1 7届一班 焦毓琦

光谱、能级和能级图的理解和应用

■河南省三门峡市外国语高中1 7届一班 焦毓琦

在2 0 1 7年高考中,原子结构相关内容将成为必学必考内容之一,因此同学们应该从现在起就投入更多的精力在学习或复习相关知识上,并从以下三个方面来理解和应用光谱、能级和能级图等。

一、掌握玻尔理论的基本内容

1.轨道量子化:核外电子只能在一些分立的轨道上运动,且这些分立的轨道半径满足关系式rn=n2r1(n=1,2,3,…)。

2.能量量子化:原子只能处于一系列不连续的能量状态,且这些量子化的能量值满足关系式

3.吸收或辐射光子的能量量子化(频率条件,又称辐射条件):原子在两个能级之间跃迁时只能吸收或辐射一定频率的光子,其光子的能量由前后两个能级的能量差决定,即h ν=Em-En。

4.氢原子的能级图如图1所示,图中自上而下原子的能量依次减小,两能级的间隔表示它们的能量差。

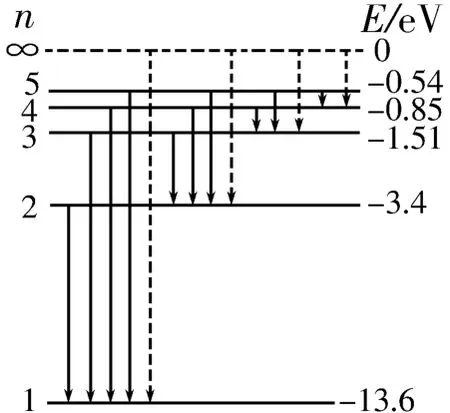
图1

已知氢原子基态的能量为E1(E1＜0),激发态的能量其中n=2, 3,…。用h表示普朗克常量,c表示真空中的光速。氢原子吸收了某光子后从第一激发态电离,电离后电子的动能为Ek,求光子的波长。

解析：氢原子第一激发态的能量是电离相当于把电子“移到”无穷远处,即n→∞,能量E∞=0,并获得动能Ek。由能量守恒定律可知,电子从第一激发态吸收的光子的能量一部分用来电离,一部分用来获得动能。由解得光子的波长

题后反思：求解本题的关键,一是弄清物理情景和能量关系,物理情景如图2所示,其中基态的能量为E1,第一激发态的能量为并非n=1的基态的能量E1;二是明确物理量的正负,基态的能量最高为0,其他能级的能量均为负值,而已知基态的能量为E1(E1＜ 0),那么第一激发态的能量也为负值,不需要再加负号。

图2

二、区别对待原子的能级跃迁规律

在玻尔理论中,原子跃迁的条件h ν= E初-E末只适用于光子和原子作用而使原子在各定态之间跃迁的情况,对于光子和原子作用而使原子电离或实物粒子与原子作用而使原子激发的情况,则不受该跃迁条件的限制。这是因为原子一旦电离,原子结构即被破坏,因而不再遵守原子结构的有关理论。对于氢原子来说,基态氢原子的电离能为1 3.6e V。只要大于或等于1 3.6e V的光子都能被基态的氢原子吸收而发生电离,只不过入射光子的能量越大,原子电离后产生的自由电子的动能就越大;对于实物粒子和原子碰撞的情况来说,因为实物粒子的动能可以全部或部分地被原子吸收,所以只要入射粒子的动能大于或等于原子某两定态能量之差,也可以使原子受激发而向较高能级跃迁。

如图3所示,一群氢原子处于n=4的激发态上,已知普朗克常量h=6.6 3-34J·s,求:

(1)这群氢原子可能释放出几种频率的光子?

(2)这群氢原子发出的光子中波长最短的是多少?

解析：(1)大量的处于某一激发态的原子向低能级跃迁时,在任意两个能级间都能放出一种特定频率的光子,因此由组合规律得C24= 6条。

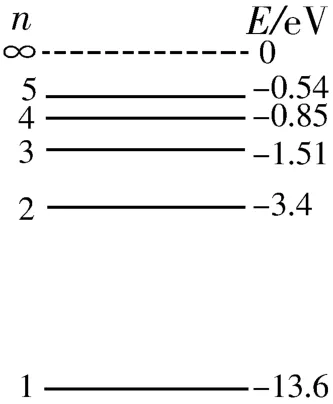
图3

(2)由频率条件h ν=E初-E末得E初-E末,从n=4跃迁到n=1时辐射的光子频率最大,波长最短,所以9.7 5×1 0-8m。

做一做：如果将例2改为一个处于能级n=4的氢原子在向低能级跃迁时,那么最多可以放出( )种频率的光子。

A.3 B.4 C.5 D.6

提示：切忌贸然套用公式C24,计算出6种。这是因为没有看清题目中的条件是“一个氢原子”。一个氢原子在跃迁时,只有按照下列方式跃迁放出的光子才最多,即先从n= 4跃迁到n=3,释放一个光子;再从n=3跃迁到n=2,释放一个光子;最后从n=2跃迁到n=1,释放一个光子。因此总共可释放3个不同频率的光子。

三、重视原子结构与其他知识的联系

氢原子放出一个光子后,根据玻尔理论易知氢原子的( )。

A.核外电子的电势能增大

B.核外电子的动能增大

C.核外电子的转动周期变大

D.氢原子的能量增大

解析：根据玻尔理论可知,氢原子由能量较高的定态跃迁到能量较低的定态要辐射出光子,氢原子的能量减少,选项D错误。氢原子放出一个光子后,核外电子进入较低能级轨道运行,半径变小。由可知,随着r的变小,电子的线速度变大,电子的动能增大,再由可知,r变小,线速度v变大,T变小,选项B正确,C错误。当电子由半径较大的轨道跃迁到半径较小的轨道时,电场力做正功,电子的电势能变小,选项A错误。答案为B。

题后反思：原子结构易与其他内容结合在一起进行考查,同学们在遇到这类问题时,只要认真审题,抓住知识间的联系,顺藤摸瓜,就会很容易地找到突破口。

(责任编辑 张 巧)

(上接第3 1页)

如图4所示,墙角固定着一根轻质弹簧,质量为m的物块与弹簧接触并压缩弹簧,此时弹簧的弹性势能为Ep。质量M= 2m的足够高的光滑圆弧形滑槽静止在光滑水平面上,滑槽底端与水平面相切。现释放弹簧,重力加速度为g,求物块能冲上滑槽的最大高度。

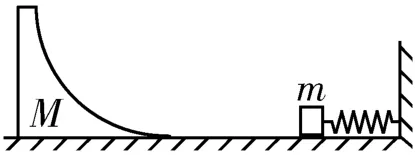
图4

解析：释放弹簧,物块在被弹开的过程中满足物块冲上滑槽,达到和滑槽速度相等时,高度最大,系统在水平方向上的动量守恒有m v0=(M+m)v,系统的机械能守恒有联立以上各式解得

点评:本题虽然涉及物块离开弹簧时的速度v0,但根据可以不必计算v0,而用直接代入,从而大大简化了解题过程。

(责任编辑 张 巧)