数学思想在解三角形中的应用

■广东省信宜砺儒中学 伍玲华

数学思想在解三角形中的应用

■广东省信宜砺儒中学 伍玲华

纵观近几年的高考题,对于解三角形这一考点,往往与三角函数、平面向量、函数性质、不等式性质等知识进行交汇命题。试题的设计主要体现了以下四种数学思想:数形结合思想、函数与方程思想、转化与化归思想和分类讨论思想。下面将详细阐述这四种数学思想在解三角形中的应用。

一、数形结合思想

数形结合思想是数与形之间的对应关系,通过数与形的相互转化,将抽象的数学语言与直观的图形结合起来解决问题的思想方法。数形结合思想是解决许多数学问题的有效思想,利用数形结合能使“数”和“形”统一起来,以形助数,以数辅形,可以使许多数学问题变得简易化。

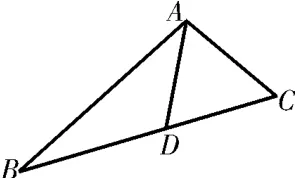
图1

如图1,在△A B C中,D是边B C上的点,且A C=C D,2A C=A D,A B=2A D,则s i nB等于( )。

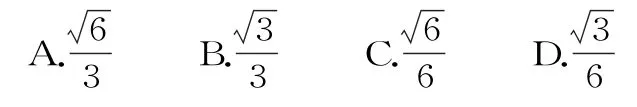
解析：根据题意,设A D=2x,则A C= C D=x,A B=4x。在△A D C中,由余弦定理可得所以s i n∠A D B=s i n∠A D C=在△A D B中,由正弦定理得

点评:本题主要考查解三角形及正余弦定理的应用。先根据2A C=A D,设出A D=2x,从而A C,C D,A B均可用x来表示,达到变量的统一,因此只需列出等式求出x的值即可。由余弦定理求出c o s∠A D C,接下来由∠A D B和∠A D C互补,得出其正弦值相等,再从△A D B中使用正弦定理,从而求出s i nB。

二、函数思想

函数思想是指从题目的已知条件出发,通过联想,构造函数模型,利用函数的性质和图像解决问题。在解三角形中,主要通过与向量、三角函数性质等结合,解决求角或边的问题。

(1)写出c o sA与c o sQ的关系式;

(2)设△P A B和△P Q B的面积分别为S和T,求S2+T2的最大值。

解析：(1)在△P A B中,由余弦定理知P B2=P A2+A B2-2P A·A B·c o sA=4-2c o sA。同理,在△P Q B中,P B2=2-2 c o sQ。所以4-2c o sA=2-2 c o sQ,所以c o sQ=c o sA-1。

点评:本题运用余弦定理、三角形面积公式建立函数模型,运用二次函数性质解决问题。

三、方程思想

方程思想是从分析问题中的数量关系入手,运用数学语言将问题中的条件转化为数学模型(方程、不等式或方程与不等式的混合组),然后通过解方程(组)或不等式(组)来使问题获解。

(1)求角A的值;

解析：(1)由题意知m·n=s i nA+ c o sB=0。

点评:(1)由两向量的坐标及两向量垂直,可得s i nA+c o sB=0,根据C的度数,利用三角形内角和求出B的度数,代入关系式可得A的度数;(2)设,由得由A的度数与C的度数相等,得出在△A B D中,利用余弦定理列出关于x的方程,求出方程的解得到x的值,即可求出A B与B C的长,利用公式可求出△A B C的面积。

四、转化与化归思想

在研究、解决数学问题时,当思维受阻时考虑寻求简单方法或从一种情形转化到另一种情形,从而使问题得到解决,解三角形主要利用正、余弦定理,通过“边化角、角化边、切化弦”的思想对问题进行转化,转化为熟悉的三角恒等变换、三角函数、平面向量等问题,再进行求解。

在△A B C中,角A,B,C所对的边分别是a,b,c。已知(b-2a)c o sC+ cc o sB=0。

(1)求C;

解析：(1)由已知及正弦定理得(s i nB-2 s i nA)· c o sC+s i nCc o sB=0,即s i nBc o sC+ c o sBs i nC=2 s i nAc o sC,即s i n(B+C)= 2 s i nAc o sC,所以s i nA=2 s i nAc o sC。

(2)余弦定理c2=a2+b2-2a bc o sC,联立方程组解得a=1,b=3。

点评:对于解决三角形边角关系的问题,常用转化与化归思想,利用正弦定理和余弦定理将边角混合的式子化为仅有边或角的等式,再根据题意求解。

五、分类讨论思想

当问题所给的对象不能进行统一研究时,我们就需要对研究的对象进行分类,然后对每一类分别研究,最后综合各类的结论得到整个问题的解答。分类讨论时应注意理解和掌握分类的原则、方法与技巧,做到“确定对象的全体,明确分类的标准,不重复、不遗漏地分类讨论”。

在△A B C中,内角A,B,C所对的边长分别是a,b,c。

(2)若s i nC+s i n(B-A)=s i n2A,试判断△A B C的形状。

解析：(1)已知c=2,C=,由余弦定理c2=a2+b2-2a bc o sC,得a2+b2-a b=4。

(2)由s i nC+s i n(B-A)=s i n2A,得s i n(A+B)+s i n(B-A)=2 s i nAc o sA,即2 s i nBc o sA=2 s i nAc o sA,即c o sA· (s i nA-s i nB)=0,所以c o sA=0或s i nA-s i nB=0。

当s i nA-s i nB=0时,得s i nB= s i nA,由正弦定理得a=b,即△A B C为等腰三角形。

故△A B C为等腰三角形或直角三角形。

点评:本题综合考查正弦定理、余弦定理、三角函数、三角形的面积公式,考查同学们的推理和计算能力。在解题过程中要特别注意隐含条件,如三角形中角的取值范围为(0,π),内角和为π;在运算过程中注意分类讨论,如等式两边除以相同的因式要注意因式是否为零,正弦函数在(0,π)上不单调,一个三角函数值对应两个角,但要注意验证是否符合题意。