三角解答题集锦

■江苏省盐城市时杨中学 刘长柏

三角解答题集锦

■江苏省盐城市时杨中学 刘长柏

三角函数具有完备的函数性质,又因其本身具备三角公式及其变换,使三角函数问题层次分明、富于变化。因此,有关三角函数的解答题是历届高考的命题热点,以三角函数为载体的立意新颖的应用问题一直受到命题者的青睐。

考点1：考查三角函数的图像和性质

三角函数的图像和性质是三角函数内容的重要组成部分,主要涉及三角函数的解析式的探求、图像变换、三角函数的性质(如定义域、值域、单调性、奇偶性、周期性、对称性等)。具体可以从两个角度来理解和求解有关的性质问题。一是从“数”的角度,一定要将正弦函数、余弦函数、正切函数的性质记清楚。二是从“形”的角度,即能够通过函数图像来描述相应的函数性质,能够通过图像的运动情况来研究和解决相应的性质问题。

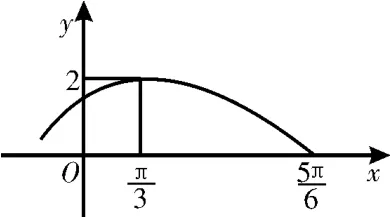
图1

(1)求函数y=f(x)的解析式;

解析：(1)由图像知A=2。

练习题1已知函数f(x)=

(Ⅰ)求f(x)的最大值和最小值;

解析：(Ⅰ)

所以f(x)max=3,f(x)min=2。

故m＞f(x)max-2且m＜f(x)min+2,得1＜m＜4,即m的取值范围是(1,4)。

考点2：三角函数与三角形“接触”以三角函数为载体,考查解三角形的问题,给出边角的三角关系,求角或边的取值范围、最值问题,以及判断三角形的形状等,主要考查三角变换及正弦定理、余弦定理的运用。主要求解思路是利用三角形的基础知识(如内角和定理、大边对大角等)、正(余)弦定理、面积公式等,并结合三角公式进行三角变换,从而获解,注意隐含条件的挖掘。

(2)已知△A B C的内角A,B,C对应的边分别为a,b,c,若且a=4,b+ c=5,求△A B C的面积。

解析：(1)

由余弦定理知a2=b2+c2-2b cc o sA,即1 6=b2+c2-b c,即1 6=(b+c)2-3b c,因为b+c=5,所以b c=3。

点评:三角函数与解三角形的综合性问题,是近几年高考的热点。这类题型难度比较低,一般出现在第1 7或1 8题的位置,属于送分题,估计以后这类题型仍会保留,不会有太大改变。解决此类问题,要根据已知条件,灵活运用正弦定理或余弦定理,求边角或将边角互化。

练习题2在锐角三角形A B C中,角A,B,C的对边分别为a,b,c,已知s i nA=

(1)求t a nB;

(2)若b=5,求c。

解析：(1)在锐角三角形A B C中,由 s i nA=,得

所以s i nC=s i n(A+B)=s i nAc o sB+

点评:处理解三角形的综合性问题时,要根据已知条件,灵活运用正弦定理、余弦定理及三角公式,求边角或将边角互化。

考点3：三角函数与平面向量“牵手”

以平面向量知识为平台考查三角函数问题,是近几年高考题中比较“抢眼”的一种题型。主要涉及平面向量的平行、垂直、数量积、模长等与三角函数相结合,探求三角函数的值、最值、值域、单调性等问题。此类题的解题思路是转化为三角函数问题,其转化途径主要有三种:一是利用向量平行或垂直的充要条件;二是利用向量数量积的公式和性质;三是利用向量模长公式。

已知向量a=(1+s i n2x, s i nx-c o sx),b=(1,s i nx+c o sx),函数f(x)=a·b。

(1)求f(x)的最大值及相应的x的值;

解析：(1)因为a=(1+s i n2x,s i nxc o sx),b=(1,s i nx+c o sx),所以f(x)= a·b=1+s i n2x+s i n2x-c o s2x=1+

(2)由f(θ)=1+s i n2θ-c o s 2θ=,得s i n 2θ-c o s 2θ=,两边平方得1-s i n4θ=,即s i n 4θ=

点评:很多问题中的向量数量积都是“昙花一现”,其实质作用就是构造三角恒等式,为解题提供三角方程。本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明的基本能力。

练习题3 已知两个向量m=(c o sθ, s i nθ),n=(2+s i nθ,2-c o sθ),其中,且满足m·n=1。

解析：(1)依题意,得m·n= c o sθ(2+s i nθ)+s i nθ(2-c o sθ)= 2(s i nθ+c o sθ)=4 s i n =1,则

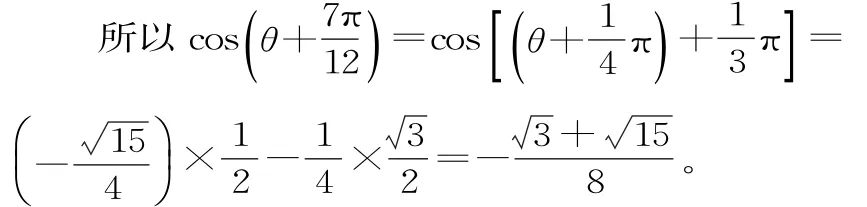
考点4：三角函数与实际应用“共舞”

三角函数应用题是以解三角形、正(余)弦定理、正(余)弦函数等知识为核心,以测量、航海、筑路、天文等为代表的实际应用问题,是高考应用题的热点题型之一。求解这类问题时,应仔细审题,提炼题目信息,恰当引入角作为参变量,将图形语言转化为与三角函数有关的符号语言,构造三角形,借助正弦定理、余弦定理、勾股定理、三角函数、不等式等知识求解。

如图2,某市拟在长为8k m的道路O P的一侧修建一条运动赛道,赛道的前一部分为曲线O S M,该曲线为函数y= As i nω x(A＞0, ω＞0),x∈[0,4]的图像,且图像的最高点为S(3, 2);赛道的后一部分为折线段MN-P,为保证参赛运动员的安全,限定∠MNP=1 2 0°。

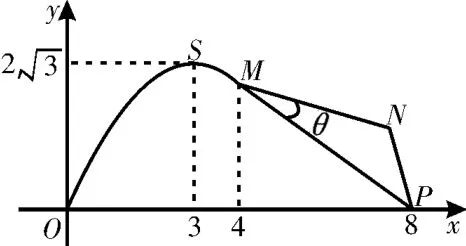
图2

(1)求A,ω的值和M,P两点间的距离;

(2)应如何设计,才能使折线段赛道MN-P最长?

解析：(1)依题意,有又所以

(2)在△MNP中,∠MNP=1 2 0°, MP=5,设∠PMN=θ,则0°＜θ＜6 0°,由正弦定理得,所以

因为0°＜θ＜6 0°,所以当θ=3 0°时,折线段赛道M-N-P最长,即将∠PMN设计为3 0°时,折线段赛道M-N-P最长。

点评:求解应用问题时,应仔细读题,细嚼慢咽,理解重点字词,抓住主干,去伪存真,真正领会条件的内涵。第(2)问中易忽视∠PMN的取值范围为(0°,6 0°),从而出现解题不严密的错误。

练习题4 如图3,游客从某旅游景区的景点A处下山至C处有两种路径。一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C。现有甲、乙两位游客从A处下山,甲沿A C匀速步行,速度为5 0 m/m i n。在甲出发2m i n后,乙从A乘缆车到B,在B处停留1 m i n后,再匀速步行到C。假设缆车匀速直线运动的速度为1 3 0m/m i n,山路A C的长为12 6 0m,经测量,

图3

(1)求索道A B的长。

(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?

(3)为了使两位游客在C处互相等待的时间不超过3m i n,乙步行的速度应控制在什么范围内?

解析：(1)因为所以所以

(2)设乙出发tm i n后,甲、乙的距离为d,则d2=(1 3 0t)2+(1 0 0+5 0t)2-2×5 0)。

乙从B出发时,甲已经走了5 0(2+8+ 1)=5 5 0(m),还需走7 1 0m才能到达C。

为了使两位游客在C处互相等待的时间不超过3m i n,所以乙步行的速度应控制在范围内。

(责任编辑 王福华)