高中数学数列试题考查题型研究

■贵州省黄平县旧州中学 吴定能

■贵州师范大学数学与科学学院 王宽明

高中数学数列试题考查题型研究

■贵州省黄平县旧州中学 吴定能

■贵州师范大学数学与科学学院 王宽明

数列作为高中数学知识的几大模块之一,为数学中离散数据的研究提供了理论支撑。在高中教材中虽然只用了少量篇幅来陈述,但由于它自身的特性功能,在各种类型的考试试题中,占据了一定的比例。为了让同学们清楚地认识高中数列试题的考查方式,本文搜集了具有一定权威性的数列试题,从考查题型的角度来分析研究数列试题。

一、客观题突出基础，重视函数性质迁移

高考关于数列的客观题考查,基本上就是考查考生对a1,d,n,an,q,Sn这五个量之间关系的掌握情况,主要有两种考查方式:一是概念、公式;二是性质。一般来说只要掌握等差(比)数列的定义、通项公式、求和公式及中项公式等,直接套用公式即可求解。若能巧用性质,可以更加快速有效地解决问题。若数列{an}的通项公式为an=k n+m(k,m为常数),是关于正整数变量n的一次表达式;或者an=k qn(k,q为常数),是关于正整数变量n的指数表达式。求数列{an}的前n项和,我们很快可以选用公式法求解。

性质：若{an}是等差(比)数列,且m+ n=p+q,则有am+an=aq+ap(am·an= ap·aq)。

特别地,若m+n=2k,则有am+an= 2ak(am·an=a2k)。

考虑到数列是一种特殊的函数,对于客观题而言,可以适当根据函数的特点进行灵活运用。

等差数列{an}的前n项和为Sn,若a1=2,S11=1 3 2,则a6=____。

解析：因为可得a1+a11=2 4。又{an}是等差数列,所以2a6=a1+a11=2 4,可得a6=1 2。

在等差数列{an}中,已知a3+ a8=1 0,则3a5+a7=____。

解析：因为a3+a8=1 0,所以a5+a6= 1 0。所以3a5+a7=2a5+(a5+a7)=2a5+ 2a6=2(a5+a6)=2 0。

其实,数列的函数性质,在习题中可以充分挖掘出来,进而迅速、直观地解决问题。如等差数列的前n项和Sn是经过原点的二次函数,其具有对称性。实践中,可利用其对称轴解题。

二、主观题突出运算，重视典型解法积累

通项公式是数列的最基本的表达方式,所以与之有关的试题也就成为重点考查题型,主要考查对求解方法的掌握情况,那么涉及的方法主要有:用公式法(待定系数)直接求通项公式;用累加(乘)法求数列的通项公式;由递推关系求通项公式;由Sn与an的关系求通项公式;用猜想归纳证明的方法来求通项公式等。

1.累加法。

累加法是等差数列通项公式的推导方法。若递推关系为an+1-an=f(n)且f(1)+f(2)+…+f(n)是可以化为特殊数列求和的。若f(n)是常数,则{an}为等差数列。

数列{an}满足a1=1,且an+1-an=n+1(n∈N*),则数列的前1 0项和为____。

分析：依据an+1-an=f(n),先用累加法求出数列{an}的通项公式,然后根据通项公式的特点,用裂项相消法求和。

解：由题可得an-a1=(an-an-1)+ (an-1-an-2)+…+(a2-a1)=n+(n-1)+ (n-2)+…+2,所以an=n+(n-1)+可得

2.累乘法。累乘法是等比数列通项公式的推导方法。若且f(1)·f(2)·…·f(n)是容易求积的,可以用累乘法求数列的通项公式。

(Ⅰ)求数列{xn}的通项公式;

(Ⅱ)记Tn=x21x23…x22n-1,证明

分析：第(Ⅰ)问按照题意就可以求解,关键是第(Ⅱ)问,根据已知我们要证需考虑通项由通项直接求积化简运算,所以需要对通项进行放缩建立不等关系。

解：(Ⅰ)过程略。

(Ⅱ)由题意结合(Ⅰ)得Tn=x21·

3.裂项相消法。

若数列{an}的通项公式能够分裂成两项之差,然后在求和表达式中有前后项可以相互抵消,这时候我们就用裂项相消法求和。常见的类型有:

已知{an}是各项均为正数的等差数列,公差为d,对任意的n∈N*,bn是an和an+1的等比中项。

(1)设 ,求证:数列{cn} 是等差数列;

解析：(1)cn==an+1an+2-anan+1=2d·an+1,cn+1-cn=2d(an+2-an+1)=2d2为定值,所以{cn}为等差数列。

(2)Tn= =c1+c3+…+c2n-1=n c1+·4d2=n c1+2d2n(n-1)。

由已知得c1=b22-b21=a2a3-a1a2= 2d a2=2d(a1+d)=4d2,将c1=4d2代入上式得Tn=2d2n(n+1)。

4.定义法。

根据数列的定义,我们可以得到an与Sn的关系为从而求出数列{an}的通项公式,这里主要谈两种类型: (1)Sn=f(n);(2)Sn=f(an)。

设数列{an}的前n项和Sn= 2an-a1,且a1,a2+1,a3成等差数列,求数列{an}的通项公式。

分析：该题属于Sn=f(an)型,利用an与Sn的关系消去Sn,得到an+1与an之间的递推关系,再选择适当方法求解。

解：已知Sn=2an-a1,则an+1=Sn+1-Sn=2an+1-2an,所以an+1=2an,所以a2= 2a1,a3=2a2=4a1。

又a1,a2+1,a3成等差数列,所以a1+ a3=2(a2+1),即a1+4a1=2(2a1+1),解得a1=2。

所以数列{an}是首项为2,公比为2的等比数列,即an=2n。

该题主要考查由Sn与an的关系求通项公式,先根据消去Sn后剩下an与an-1之间的关系或关于n的表达式,即建立新的递推关系进行求解,同时应注意讨论及验证n=1的情况。

5.错位相减法。

设等差数列{an}的公差为d,前n项和为Sn,等比数列{bn}的公比为q。已知b1=a1,b2=2,q=d,S10=1 0 0。

(Ⅰ)求数列{an},{bn}的通项公式;

分析：依据题意,第(Ⅱ)问可用错位相减法求数列{cn}的前n项和。

解：(Ⅰ)由题意知解得或故或

(Ⅱ)由d＞1,可得an=2n-1,bn= 2n-1,即

若数列{cn}的通项公式可表示为cn= an·bn,数列{an}与{bn}分别为等差数列和等比数列,等比数列的公比为q,若求数列{cn}的前n项和Sn,首先把Sn表示出来,然后构造q Sn等式,最后采用错位相减法求和。

三、信息题突出推理，重视阅读素养培养

这类题型由于情境陌生、信息量较大,同学们一般在阅读和理解方面存在某种程度的困难。同时,这类题对信息的提取、选择和知识的综合运用,以及同学们的推理能力有较高的要求。

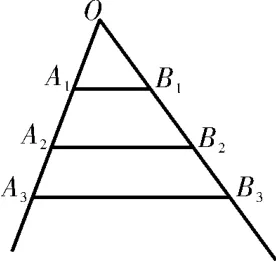
图1

如图1,互不相同的点A1,A2,…,An,…和B1,B2…,Bn,…分别在角O的两条边上,所有AnBn相互平 行,且 所 有 梯 形AnBnBn+1An+1的面积均相等。设O An=an。若a1=1,a2=2,则数列{an}的通项公式是____。

解析：设S△OA1B1=S,由已知得a1= O A1=1,a2=O A2=2,且有△O A1B1∽△O A2B2,所以所以

又所有梯形AnBnBn+1An+1的面积均相等,所以所以所以an=

近几年的高考数列题,有些是直接考查数列知识的,有些是考查有关数列知识综合运用的,有些是考查数列知识迁移的,对数列知识的了解、理解和掌握等层次的要求均有涉及。实践中,需要同学们加强对知识的理解,强调与其他内容的融合,尤其是函数、不等式等方面的内容,同时也需要同学们记住并且掌握典型的方法。如此,同学们方可从容面对高考,面临信息题时,也能处变不惊,充分发挥自己解决问题的能力。

(责任编辑 王福华)