基于小波包样本熵和SVM的水泵机组振动故障诊断

陈英强，陈煜敏，蒋 劲，符向前，肖志怀，赖冠文，张嘉勋

(1.武汉大学 动力与机械学院，武汉 430072；2.武汉大学 电气工程学院，武汉 430072；3. 广东省水利厅，广州 510000)

水泵机组故障诊断是指根据采集到的水泵机组运行信号，判断机组的运行状态，是正常、异常还是故障状态。当机组处于异常或故障状态时，可以根据收集的信息分析故障原因，提取故障的特征；并针对对应的故障给出维修决策[1]。由于水泵机组工作原理和机组结构的复杂性和特殊性，引起机组故障的原因往往错综复杂，因为水泵机组同一台机组各部件间都是紧密耦合且互相关联的，各不同设备间也都存在着紧密的联系，在生产运行中形成一个各部件相互耦合的整体。当故障发生时，其症状和原因之间常表现出很强的随机性和不确定性。因此，如何利用实时的状态信息中的有用信息尽早识别出故障的种类是很有必要的。这种方法可以改变传统的水泵机组检修方式，传统水泵检修方式是定期维护和事后维修[2]，这种检修方式具有很大的被动性，并且经常会造成过度维修，定期维护中很多机组状态良好，但是依然需要检修，这造成不必要的经济损失，有些机组已经出现故障，但直到定期维护时才发现，错过了最佳的维修期。对于状态良好的机组，在检修后反而出现状态不良，如果能够根据机组的实时运行信息，实时监测其运行状态，将被动维修变成主动维修，这样就能够尽早发现故障，降低泵站损失，减少不必要的维修费用，降低运行成本。因此提出一种有效的泵机组振动故障识别方法是很有必要的。

1 样本熵

样本熵[3]是Richman等人提出的一种新的算法，是对近似熵的一种改进，是一种不计自身匹配的统计量。与近似熵相比，样本熵对数据长度的依赖性更小，同时具有更好的抗干扰能力。一般地，对于由N个数据组成的时间序列{x(n) }=x(1),x(2), …,x(N),样本熵的计算方法如下[4]：

(1)按序号组成一组维数为m的向量序列，Xm(1),…,Xm(N-m+1)，其中Xm(i)={x(i),x(i+1),…,x(i+m-1) },1≤i≤N-m+1。这些向量代表从第i点开始的m个连续的x的值。

(2)定义向量Xm(i)与Xm(j)之间的距离d[Xm(i),Xm(j)]为两者对应元素中最大差值的绝对值。即：

d[Xm(i),Xm(j)]=maxk=0,…,m-1[|x(i+k)-x(j+k)|]

(1)

(3)对于给定的Xm(i)，统计Xm(i)与Xm(j)之间距离小于等于r的j(1≤j≤N-m,j≠i)的数目，并记作Bi。对于1≤i≤N-m，定义Bmi(r)=Bi/(N-m-1)。

(4)定义B(m)(r)为：

(2)

(5)增加维数到m+1，计算Xm+1(i)与Xm+1(j)(1≤j≤N-m,j≠i)距离小于等于r的个数，记为Ai。Ami(r)定义为：Ami(r)=Ai/(N-m-1) 。

定义Am(r)为：

(3)

这样，Bm(r)是两个序列在相似容限r下匹配m个点的概率。而Am(r)是两个序列匹配m+1个点的概率。样本熵定义为：

(4)

样本熵的计算过程很明显地反映出m，r取值对于样本熵值的巨大影响。根据Pincus的研究结果[5]，当m=1或2,r=0.1Std～0.25Std(Std是原始数据的标准差)时计算得到的样本熵值具有较为合理的统计特性。本文中，m=1，r=0.1Std。

2 支持向量机理论

支持向量机[6,7](Support Vector Machines，SVM)是在统计学习理论(Statistical Learning Theory，SLT)的基础上发展起来的一种新的机器学习方法。它通过最大化样本的分类间隔，使样本点的区分度最大，最终取得实际风险最小。其基本思想是：当线性可分时在原空间寻找两类样本的最优超平面；当线性不可分时，引入松弛变量，通过非线性映射将低维输入空间的样本映射到高维空间进行线性分析并寻找最优分类超平面。使用结构风险最小化原则在属性空间构建最优分类超平面，使得分类器达到全局最优并在整个样本空间的期望风险以某个概率达到一定上界。

SVM有以下几个优点：

(1)基于结构风险最小化原则和VC维理论，泛化能力强，可由有限的样本训练得到小误差分类器，对独立测试集的训练误差也很小；

(2)求解问题对应的是凸优化问题，局部最优解一定是全局最优解；

(3)应用核函数将非线性问题转化为线性问题；

(4)分类间隔最大化，因而具有较强稳健性。

由于SVM的这些优点，使得它成为模式识别、线性回归等领域强有力的机器学习工具。

SVM的结构如图1所示，它由三层组成：输入层输入并存储样本数据(x1,x2,…,xi)，不参与其他加工运算；中间层接受由输入层传来的数据，并通过核函数将非线性问题的样本变换到高维空间中，将非线性回归变成高维空间的线性回归问题；输出层构造拟合函数f(x)，输出中间节点的线性组合，每一个中间节点对应一个支持向量。

图1 SVM结构Fig.1 Structure of SVM

3 基于小波包样本熵与SVM的故障诊断方法

本文所述的诊断方法是将采集得到的不同振动状态的信号经过小波包分解，以样本熵和SVM进行定性定量的故障识别，具体步骤如下：

(1)利用小波包将降噪后的数据进行2层分解，得到4个不同的频带；

(2)对不同频带进行重构，然后求出不同频带的样本熵值，记作V=[SamEn1,SamEn2,SamEn3,SamEn4]；

(3)选出部分样本熵值作为训练样本，使用SVM对样本进行分类；

(4)以SVM作为模式分类器，识别故障类别。

4 实验验证

4.1 实验台介绍

实验系统由转子实验台、信号采集系统及数据处理软件等构成。其中转子试验台通过电机驱动质量圆盘，在轴承约束下随转轴转动，通过激光传感器测量转子转速，通过电磁传感器测量转轴x、y方向位移。通过人为地制造不对中量、不平衡及定子碰磨，以模拟实际中存在的不对中不平衡及定转子碰磨实验，转子实验台结构如图2所示。其中转速传感器置于电机与最上端轴承之间，位移传感器测量距上端质量圆盘2 cm处转轴x、y两方向振动位移量。两转轴间采用可允许少量不对中量存在的柔性联轴器相连接。单此实验数据采集过程中保证转速及特征故障量不发生改变，信号采集频率1 000 Hz，采集时间为7.2 s。图3～6是4种状态下采集到的原始数据的时域图。

图2 实验系统Fig.2 The experiment system

图3 正常状态Fig.3 The normal condition

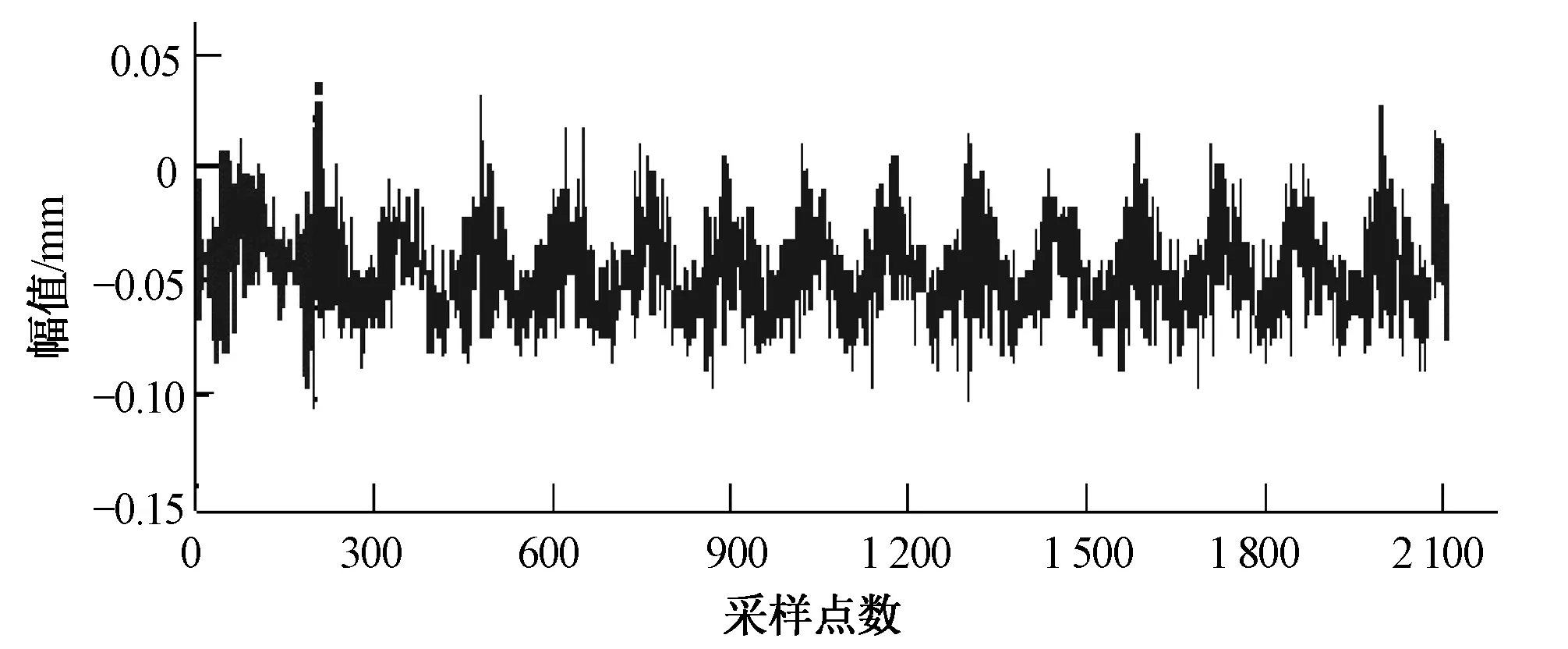
图4 不平衡状态Fig.4 The unbalanced condition

图5 不对中状态Fig.5 The misalignment condition

图6 碰摩状态Fig.6 The rub-impact condition

4.2 提取样本熵值

通过上述的立式转子试验台，模拟立式水泵在实际运行的过程中由于水力、机械、电力[8,9]等原因造成的振动，分别模拟了正常状态、不平衡状态、不对中状态及碰摩状态下泵的振动。并通过本文的方法对采集的信号进行分解，求出样本熵，以下是部分样本熵熵值分布特征。

图7 频带1的样本熵值Fig.7 Sample entropy of band 1

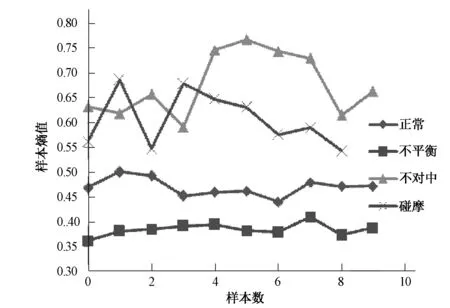
图8 频带2的样本熵值Fig.8 Sample entropy of band 2

图9 频带3 的样本熵值Fig.9 Sample entropy of band 3

图10 频带4的样本熵值Fig.10 Sample entropy of band 4

4.3 基于SVM的振动故障诊断

SVM分类方法根据指导思想可以分成两大类，一类是将多类问题分解成两类可直接解决的问题，然后进行判别；另一类是计算出多类分类决策函数一次的实现多种分类。在实际应用中第二种思想很难实现，基本都是基于第一种思想[10]。基于第一种思想，主要有五种分类方法，分别为一对其余法、一对一、DAG方法、决策树方法以及纠错输出编码法[11,12]。本文采用的方法是“一对一”。“一对一”的思想[13]是在所有训练集中找到不同类别的两两组合然后进行两类问题的求解。

具体做法是针对正常、不对中、不平衡及碰摩这4种状态训练出6种分类器，然后用四种状态的一种作为测试样本，对6种分类器进行测试。本次实验采集的数据，其中60%作为训练样本，40%作为测试样本。首先利用小波包样本熵提取振动故障的特征信息，然后利用分类器识别故障的种类，下表是测试样本诊断结果的准确度。

表1 诊断结果表Tab.1 Table of diagnostic results

从表1中可以看出本故障诊断方法的正确率比较高的，对于不对中和不平衡的识别可以达到100%，而对于碰摩故障的识别不能达到100%，但是，也达到了95%以上。从各个故障的机理中分析可以看到，对于不对中和不平衡两种故障而言属于单一故障，而本实验中的碰摩由于人为制造出的(如图11)，这种人为制造的故障属于耦合故障，其耦合了不平衡和不对中两种故障，因此故障特征提取的过程中与其他状态有一定的重合，所以碰摩故障的故障识别不能达到100%。

图11 碰磨故障设置Fig.11 Rubbing fault setting

水泵机组运行的实际环境中通常故障产生不是单一故障，而是多种因素的耦合结果，即便是这种情况本文所述的研究方法依然能够应用，随着训练样本的增多，分类器会不断地扩充库容量，对于故障识别的准确度会有一定的帮助。

5 结 语

利用小波包样本熵提取故障特征，并求得相应样本熵值，选取部分样本熵值进行支持向量机一对一的故障库训练，以此作为故障库对故障进行识别，本方法对测试数据有较高的识别度，实验结果表明基于小波包样本熵和SVM水泵机组振动故障诊断的方法具有较高的可信度。

□

[1] 刘晓亭, 冯辅周. 水电机组运行设备监测诊断技术及应用[M].北京: 中国水利水电出版社, 2010.

[2] 陈喜阳．水电机组状态检修中若干关键技术研究[D]．武汉：华中科技大学，2005.

[3] Richman J S, Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy [J]. American Journal of Physiology-Heart and Circulatory Physiology, 2002,278(6):2 039-2 049.

[4] R Alcaraz,J J Rieta. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms[J]. Biomedical Signal Processing and Control, 2010.

[5] Raffa F A，Vatta V. The dynamic stiffness method for linear rotor-bearing system[J]. ASME Journal of Vibration and Acoustics,1996,118(7):332-339.

[6] Pincus S M. Assessing serial irregularity and its implications for health [J]. Ann. N. Y. Acad. Sci, 2002,954:245-267.

[7] 平 源. 基于支持向量机的聚类及文本分类研究[D]. 北京：北京邮电大学 2012.

[8] 彭 璐. 支持向量机分类算法研究与应用[D]. 长沙：湖南大学 2007.

[9] 瞿 曌，赖 旭,盛 旺．水电机组状态检修模式探讨[J]．华东电力，2008，(1):109-111.

[10] 王洪杰，刘全忠，季天晶，等. 锅炉给水泵故障机理及诊断技术的研究[J]. 节能技术, 2004, 22(6):30-31.

[11] 丁世飞，齐丙娟，谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011,40(1):2-10.

[12] 吴兴伟，王 雷，迟道才. 基于多分类SVM的水泵故障诊断的研究[J]. 节水灌溉, 2009,(7):37-39.

[13] 张 炜，张 磊，李 亮. 基于GA优化的SVM涡轮泵故障诊断[J].液压与气动, 2009,(1):84-86.

[14] 苟 博，黄贤武. 支持向量机多类分类方法[J]. 数据采集与处理, 2006,21(3):334-339.