基于BA-LSSVM模型的月径流预测方法
武群丽,彭晨阳
(华北电力大学 经济与管理学院,河北 保定 071003)
准确可靠的月径流预测对水资源系统有效运行管理具有重要意义。由于受到气候变化和人类活动等众多因素的影响,河川径流表现出非线性的复杂特性,因此对其未来趋势的预测成为了水资源研究领域的难点问题[1]。近年来,计算机技术的飞速发展极大地丰富了径流预测的研究方法,如人工神经网络模型[2,3],支持向量机[4,5]等非线性方法。神经网络模型存在易陷入局部最优、过学习、泛化能力差等缺点[6]。水文时间序列通常是非线性的小样本数据,支持向量机方法在小样本数据情况下预测效果仍优于传统模型和神经网络模型[7]。但由于SVM算法存在超平面参数选择问题,致使其求解规模过大。为此,Suykens[8]等人提出了最小二乘支持向量机算法。李佳[9]、李彦彬[10]、崔庆[11]、周秀平[12]等基于最小二乘支持向量机的建立径流量预测模型,预测实例表明LSSVM在处理小样本数据预测问题上有效地避免了神经网络方法的易陷入局部最优和过学习现象等问题。
随着人工智能技术的蓬勃发展, LSSVM模型获得广泛地关注。而正则化参数γ和核函数参数σ2对LSSVM模型的学习和适应能力有直接影响,所以一些研究在进行径流预测分析时利用智能算法对LSSVM模型进行参数优化。李文莉等[13]和代兴兰[14]分别使用粒子群算法和遗传算法对LSSVM模型的学习参数进行寻优。然而,这些算法比较容易陷入局部最优,搜索到局部极小值。为了弥补现有算法的不足,Yang[15]提出了一种基于种群的随机寻优算法—蝙蝠算法(BA)。蝙蝠算法完美结合了粒子群算法、遗传算法的主要优点,使得蝙蝠算法具有模型简单、搜索能力强、收敛速度快等优点,因此蝙蝠算法已广泛应用到研究中[16-17]。鉴于蝙蝠算法在准确性和有效性方面较其他算法有很大优势,本文使用BA对LSSVM模型的正则化参数和核函数参数进行选择并获得全局最优解。
1 研究方法与数据来源
1.1 蝙蝠算法
蝙蝠算法(BA)是基于蝙蝠的回声定位理论形成的一种元启发式优化智能算法,为研究便利做出如下假设:
(1) 蝙蝠运用回声定位感应距离,并能以某种方式感知猎物和障碍物的差异;
(2) 蝙蝠在Xi位置以速度Vi随机飞行,以固有频率fmin、可变波长λ和响度A0搜索食物,它们能够自动的根据食物与自身的距离调节发射的脉冲波长(或频率),并在靠近食物时调整脉冲的频度γ∈[0,1];
(3) 假定响度的变化从最大值A0(正值)到最小值Amin。
蝙蝠算法的基本步骤表示如下:
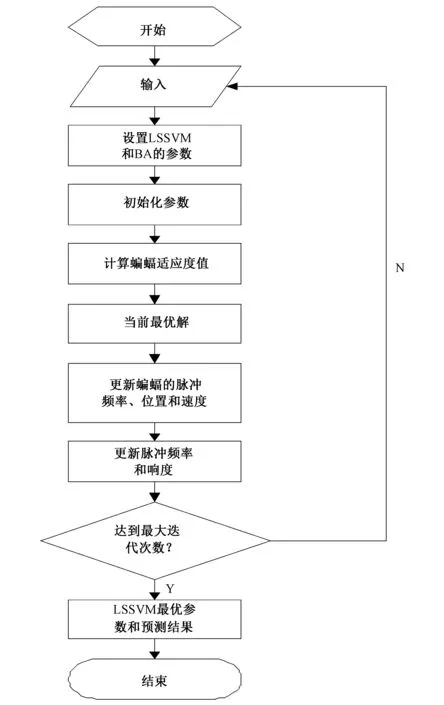
①初始化蝙蝠种群xi和vi(i=1,2,…,n);②初始化频率fi,发射频度ri和响度Ai;③While (t<最大迭代次数);④通过调整频率产生新解;⑤更新速度和位置;⑥If (rand >ri);⑦从最优解集中选择一个解;⑧从选择的这个最优解附近产生一个局部解;⑨End if;⑩通过随机飞行产生一个新解;If [rand 最小二乘支持向量机(LSSVM)是标准支持向量机(SVM)的一种改进算法,采用与SVM不同损失函数,用等式约束代替不等式约束,同时最小化误差的平方项。它将解二次规划问题转化为求解线性方程组的问题,有效提高了标准支持向量机的训练速度和精度。设样本训练集S={(xi,yi)|i=1,2,3,…,t},其中xi∈Rn,yi∈R。最小二乘支持向量机的基本思想是使用一个非线性映射函数将数据映射到一个高维特征空间,然后在高维空间进行线性回归,最后映射回原空间完成输入空间的线性回归,其线性回归函数可以表示为: f(x)=ωTφ(x)+b (1) 式中:φ(x)为核空间映射函数;ω为权向量;b为常数。 根据结构风险最小化原则确定参数ω,b,则有: (2) 式中:‖ω‖2表示模型的复杂程度;γ是正规化参数;Remp为经验风险函数;LSSVM是化目标函数为误差ξi的二次项,故优化问题转化为: (3) s.t.yi=ωφ(xi)+ξi+b,i=1,2,3,…,t 式中:ξi为预测误差,用拉格朗日法求解该问题,则有: (4) 式中:λi(i=1,2,3,…,t) 是拉格朗日乘子。 根据Karush-Kuhn-Tucker(KKT)优化条件,可得: (5) 上述优化问题可转化为求解线性方程: 式中:λ=[λ1,λ2,…,λt]T;I=[1,1,…,1]T为t×1维列向量;y=[y1,y2,…,yt]T,Jij=φ(xi)Tφ(xj)=K(xi,xj),K为满足Mercer条件的核函数,最后得出预测模型的函数为: (7) 这里采用径向基函数(RBF)作为核函数。 (8) 式中:σ2为核函数参数。 在选定核函数之后,LSSVM需要选取正则化参数γ和核参数σ2,在现存的文献中,这两个参数大多还是凭个人经验、实验对比或者网格搜索法及交叉验证等方法进行寻优,这样做耗时,效率低下而且预测结果不佳。而在本文中采用蝙蝠算法(BA)优化这两个参数,可进一步改善了模型的适应性,有效提高预测精度。 基于BA算法的LSSVM的参数优化步骤如下: (1)参数设置。蝙蝠参算法的主要参数:蝙蝠种群大小n,最大迭代次数N,蝙蝠的响度A,脉冲频率r,蝙蝠位置向量x,速度向量v。 (2)种群初始化。初始化蝙蝠种群的位置,每一个蝙蝠位置由LSSVM参数组合(γ,σ)构成,公式如下: x=xmin+rand(1,d)×(xmax-xmin) (9) 式中:种群的维数d=2。 (3)更新参数。计算种群适应度,找出当前最佳解,同时更新蝙蝠的飞行速度、脉冲频率和位置,方法如下: fi=fmin+(fmax-fmin)β (10) vti=vt-1i+(xti-x*)fi (11) xti=xt-1i+vti (12) 式中:β∈[0,1]是均匀分布的随机数;fi∈[fmin,fmax]是蝙蝠 的搜索脉冲频率;vti、vt-1i分别表示蝙蝠i在t和t-1时刻的速度;xti、xt-1i分别表示当前蝙蝠i在t和t-1时刻的位置;x*表示当前所有全局最优解。 (4)更新蝙蝠个体。如果有rand>ri,则对当前种群中最优蝙蝠x*进行随机扰动,产生新的蝙蝠个体;如果rand At+1i=αAti (13) rt+1i=r0i[1-exp(-γt)] (14) 式中:0<α<1,γ>0均为常数。 (5)输出全局最优参数。对种群的所有蝙蝠的适应度值进行排序,找出当前最优解,重复步骤(2)至(4),到最大迭代次数终止,输出全局最优参数,建立月径流预测模型。 综合以上所述步骤,可将BA-LSSVM算法流程用图1表示。本文选择月降水量作为预测月径流的输入变量。首先,利用LSSVM模型训练原始数据,以预测值与真实值的均方误差作为蝙蝠算法的适应度值。然后通过蝙蝠算法(BA)寻找LSSVM的群体最优参数。最后,获取最优化参数的LSSVM模型用来预测月径流。 图1 BA-LSSVM模型流程图Fig.1 Flowchart of BA-LSSVM 本文选取了位于西江流域内的柳州水文站2000-2014年实测月径流资料作为研究对象。西江流域是珠江水系的主干流,上游南盘江发源于云南省沾益县内的马雄山。而珠江流域是我国南方的重要水系,年径流量仅次于长江流域,居全国第2位。西江流域面积为35.21 万km2,占珠江流域总面积的77.8%[18]。西江流域是湿热多雨的热带、亚热带气候,大部分地区的年平均温度在14~22 ℃之间,多年平均湿度在71%~80%,西江流域多年平均降雨量1 200~2 200 mm[19]。西江流域是广东省和广西省的经济、文化和政治中心。对西江流域内的柳州水文站的月径流进行预测,可为西江流域内水资源管理提供科技支撑,更好地实现水资源的可持续发展。本文以2000-2011年各月径流量作为训练样本,以2012-2014年各月径流量为测试样本。研究期内各月径流量如图2所示。 图2 2000-2014年各月径流量Fig.2 Monthly runoff data from 2000 to 2014 本文选用确定性系数(Dy)、均方根相对误差(RMSE)、平均绝对误差百分比(MAPE)3个指标作为评价各种模型预测效果的依据。根据水文情报预报规范[20],确定性系数DY值越大,模型精度越高。各评价指标计算公式如下: (17) 在实际应用中,LSSVM模型的性能依赖于其参数的选择,要建立最优化的预测模型,必须进行参数寻优。BA 作为一种新的群智能优化算法为LSSVM参数的优化提供了新的思路。本文中的LSSVM 模型选用径向基函数(RBF)作为核函数,RBF函数的参数相对较少,且数值限制条件少,可以降低模型的复杂程度,提高训练速度,正则化参数γ和核函数参数σ2由BA自动搜索进行优化。BA的主要参数如表1所示。 表1 BA的主要参数Tab.1 Main parameters of BA 另外,为验证BA-LSSVM模型良好的预测性能,本文同时使用粒子群算法优化LSSVM模型的参数(PSO-LSSVM),网格搜索与交叉验证算法优化的LSSVM模型,以及BP神经网络模型进行对比。BP神经网络的学习速率取0.01,循环次数取300,采用“试错法”确定隐含层节点数为11。PSO-LSSVM模型的最大迭代次数为200,初始粒子群数为30。LSSVM模型的正则化参数γ和核函数参数σ2如表2所示。 表2 LSSVM模型的参数选择结果Tab.2 The related parameters of different LSSVM models 为保证模型的适用性和可靠性,本文分别采用BPNN,LSSVM,PSO-LSSVM和BA-LSSVM 4种方法对2000-2014年的月径流数据进行训练和预测。其训练样本集数为144,测试集样本数为36。测试样本的预测值与实测值如图3所示。为了便于观察和比较,表3给出了不同模型的月径流预测结果。 图3 预测值与实测值对比Fig. 3 Comparison of forecasting values and actual values 评价指标预测模型BALSSVMPSOLSSVMLSSVMBPNNDY0.98910.96680.93110.9278RMSE0.16640.31750.44820.5401MAPE/%15.1329.3141.1148.27 由图3可知,不同预测方法得出的实测值与预测值的绝对误差是不同的,BP神经网络模型的绝对误差较其他模型是最大的,而BA-LSSVM模型在绝大部分月份的预测值均是可以接受的。与使用网格搜索和交叉验证算法进行参数优化的LSSVM模型相比,通过智能算法对LSSVM模型进行参数优化得到的改进模型更适合预测月径流量。另外,与PSO-LSSVM相比,基于BA改进的LSSVM预测模型能够显著提高LSSVM模型的预测性能,表现出更好的泛化能力。 由表3可非常直观的评价不同模型的预测性能,从中可以得出:本文建立了两个改进的LSSVM模型(BA-LSSVM,PSO-LSSVM),就 、RMSE、MAPE三个评价指标而言,BA-LSSVM模型达到的预测效果明显优于PSO-LSSVM混合预测模型,例如,BA-LSSVM模型的RMSE是0.166 4,而PSO-LSSVM模型的RMSE是0.317 5, BA-LSSVM模型的MAPE是15.13%,而PSO-LSSVM模型的MAPE是29.13%。这是因为BA吸收了现有智能算法的优点,同时还结合了蝙蝠惊人的回声定位能力,而粒子群算法实际是简化的蝙蝠算法的特殊情形,所以蝙蝠算法的参数寻优能力明显优于粒子群算法;BA-LSSVM和PSO-LSSVM模型的预测效果优于使用网格搜索和交叉验证进行参数优化的LSSVM模型,原因是改进的LSSVM模型加入了参数自动搜索寻优的过程,使得LSSVM模型具有更强的学习能力和泛化能力,也更易获得全局最优解; BA-LSSVM、PSO-LSSVM和LSSVM模型的预测精度都好于BPNN模型,这是因为BP神经网络具有较强的非线性映射能力,能实现对非线性函数的逼近,但容易陷入局部最优。另外,BPNN不能确保收敛到全局最优解,网络结构也不易确定,从而造成月径流预测精度较低。总体而言,本文提出的基于蝙蝠算法优化最小二乘支持向量机模型适用于非线性的径流序列分析和预测,并能显著提高了对径流序列的预测能力和预测精度,对实际的水文时序具有良好的适用性。 为对月径流量进行有效的预测,本文建立了一个组合智能模型BA-LSSVM。以月降雨量作为输入量,通过蝙蝠算法对LSSVM模型的正则化参数 和核函数参数 进行优化,最终得到具有良好学习和泛化能力的模型对2011-2014年的月径流量进行预测。 与PSO-SSVM 模型,使用网格搜索和交叉验证算法优化LSSVM模型以及BP神经网络模型相比, BA-LSSVM模型的各项精度评价指标值均较为理想,这表明BA-LSSVM具有很强的预测能力和实用性,为月径流预报研究提供了新的思路。 □ [1] 张 楠,夏自强,江 红. 基于多因子量化指标的支持向量机径流预测[J]. 水利学报, 2010,41(11):1 318-1 324. [2] Govindaraju RS. Artificial neural networks in hydrology. I: preliminary concepts[J]. Journal of Hydrologic Engineering, 2000,5(2):115-123. [3] Govindaraju RS. Artificial neural networks in nydrology. II: nydrologic applications[J]. Journal of Hydrologic Engineering, 2000,5(2):124-137. [4] 廖 杰,王文圣,李跃清,等. 支持向量机及其在径流预测中的应用[J]. 四川大学学报(工程科学版), 2006,38(6):24-28. [5] 张兰影,庞 博,徐宗学,等. 基于支持向量机的石羊河流域径流模拟适用性评价[J]. 干旱区资源与环境, 2013,27(7):113-118. [6] 卫太祥,马光文,黄炜斌. 基于惩罚加权支持向量机回归的径流预测模型[J]. 水力发电学报, 2012,31(6):35-38,43. [7] Yoon H,Jun S,Hyun Y, et al. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer[J]. Journal of Hydrology, 2011,396(1):128-138. [8] Suykens J, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999,9(3):293-300. [9] 李 佳,马光文,杨忠伟,等. 基于粒子群最小二乘支持向量机的径流预测[J]. 人民长江, 2012,43(S2):60-62. [10] 李 彦彬,尤 凤,黄 强,等. 多元变量径流预测的最小二乘支持向量机模型[J]. 水力发电学报, 2010,29(3):28-33. [11] 崔 庆,马孝义,陈海涛. 最小二乘支持向量机模型在径流预报中的应用[J]. 中国农村水利水电, 2012,(12):63-65. [12] 周秀平,李天翔,王文圣. 年径流预测的最小二乘支持向量机-马尔可夫链组合模型[J]. 水力发电学报, 2013,32(4):16-19. [13] 李文莉,李郁侠. 基于粒子群最小二乘支持向量机的水文预测[J]. 计算机应用, 2012,32(4):1 188-1 190. [14] 代兴兰. 遗传算法与最小二乘支持向量机在年径流预测中的应用[J]. 水资源与水工程学报, 2014,25(6):231-235. [15] Yang X. Nature inspired cooperative strategies for optimization (NICSO 2010)[M]. Springer, 2010:65-74. [16] Rao BV,Kumar GN. Optimal power flow by bat search algorithm for generation reallocation with unified power flow controller[J]. International Journal of Electrical Power & Energy Systems, 2015,68:81-88. [17] Hafezi R, Shahrabi J, Hadavandi E. A bat-neural network multi-agent system(BNNMAS) for stock price prediction: case study of DAX stock price[J]. Applied Soft Computing, 2015,29:196-210. [18] 袁 媛,雷晓辉,蒋云钟,等. 基于SWAT模型的西江流域径流模拟研究[J]. 中国农村水利水电, 2015,(3):14-17. [19] 童 娟. 珠江流域概况及水文特性分析[J]. 水利科技与经济, 2007,13(1):31-33. [20] GB/T22482-2008. 水文情报预报规范[S].1.2 最小二乘支持向量机
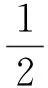
1.3 蝙蝠算法-最小二乘支持向量机模型
1.4 数据来源

2 结果与分析
2.1 模型精度评价

2.2 模型参数选取


2.3 不同模型预测结果分析


3 讨 论
4 结 语

