基于改进粗糙熵的大坝服役性态推理
郭 沂 林
(新疆兵团勘测设计院(集团)有限责任公司石河子分公司,新疆 石河子 832000)
根据大坝多源效应量监测资料,借助一定的数学理论或力学方法将各种效应量监测资料进行有机融合分析是实现大坝服役性态推理的重要手段[1,2]。多源信息融合通常分为经典贝叶斯理论等基于概率论的融合方法和粗糙集理论等非概率的融合方法[3],前者存在依赖先验条件等不足,加之大坝系统本身又存在随机性和不确定性特点,故本文从粗糙集理论改进粗糙熵的角度出发对大坝多源效应量信息进行不确定性描述和融合分析。现有若干粗糙熵研究方法主要在:①对系统不确定性描述不完备;②利用信息熵来刻画系统知识粗糙性或不确定性时,与粗糙集基本概念所描述状况相悖等方面存在的不足[4-6],借鉴已有学者研究成果[7-10],利用粗糙度度量大坝系统集合边界不确定性,利用粗糙熵度量大坝系统知识不确定性,有机结合粗糙度与粗糙熵,利用改进粗糙熵模型完成大坝系统不确定性定量度量和多源效应量权重赋值,并推理大坝服役性态。
1 粗糙集理论的基本概念
自波兰科学家Pawlak于1982年提出粗糙集概念后[11],其作为一种处理不确定性和模糊信息的重要工具,已得到了深入研究[12-14]。基于粗糙集理论,构建大坝安全评价系统(简称大坝系统):
DS=(U,A,V,f)
(1)
式中:U为非空有限论域,由待评价对象x组成,U=∪x,如待评价大坝不同年份安全属性;A为属性集合,A=C∪D,C为条件属性,C={c1,c2,…,cn},如大坝监测变形、渗流及应力应变等效应量,D为决策属性,D={d1,d2,…,dk},如大坝安全等级,借鉴文献[1],取D={正常,基本正常,轻度异常,重度异常,恶性失常},满足C∩D=Φ;V为所有属性值域的并集,V=∪Va,Va为属性a的值域;f为粗糙集理论中的代数观点[4],表示U×A→V的映射函数,对∀xi∈U,∀a∈A,存在f(xi,a)∈Va。
设U为非空有限论域,由大坝不同年份安全属性集成,R为U上的二元等价关系,或称为不可分辨关系,标记为U/ind(R)={R1,…,Ri,…},序对DS=(U,R)定义为近似空间,或大坝系统知识库,原子集Ri表示基本概念或知识模块。对于论域U上的任意子集X,由于其未必能够用知识库中的概念或模块精确的表达,故在粗糙集理论中利用X关于R的上近似集R*(X)和下近似集R*(X)来描述,并令[x]为x所在的R的等价类:
R*(X)={x∈U|[x]∩X≠Φ}
(2)
R*(X)={x∈U|[x]⊆X}
(3)
并定义集合BndR(X)=R*(X)-R*(X)为X关于R的边界域。R*(X)表示根据现有知识库精确判断出属于X的对象组成的最大集合,R*(X)表示根据现有知识库判断可能属于X的对象组成的最小集合,BndR(X)表示判断的对象可能属于X但不能精确判断一定属于X的集合。当且仅当R*(X)=R*(X),即BndR(X)=Φ时,X可由R定义;当且仅当R*(X)≠R*(X),即BndR(X)≠Φ时,X关于R是粗糙的或不确定的。为衡量近似空间的集合边界不确定性,粗糙度概念得以引入[1]。
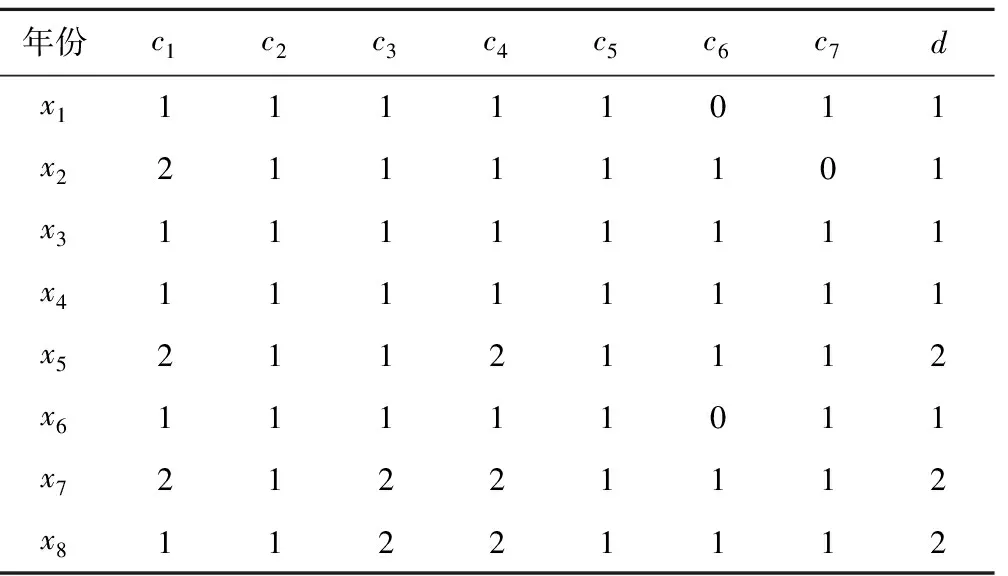
知识库B=(U,R)表示对论域 中对象 进行分类能力的表达,其认为知识是具有粒度的[1]。知识粒度越大,知识越粗糙,所含信息量越少,知识不确定性越大。若存在P,Q⊆R为U上两个不可分辨关系,若P⊃Q,则有U/ind(P)⊂U/ind(Q),记为P 根据上文分析可知,粗糙集理论中的不确定性主要有两方面原因引起:①由近似空间的集合划分引起的粗糙集的边界不确定性称为集合边界不确定性;②基于近似空间二元等价关系引起的概念或知识模块不确定性称之为知识不确定性。 针对大坝系统,在上下近似集的基础上,引入粗糙度度量集合边界不确定性。糙粗度定义为: (4) 式中:αR(X)表示近似精度;‖R‖表示集合R的基数;0≤ρR(X)≤1,当ρR(X)=0时,R*(X)=R*(X),X可由R精确定义;当ρR(X)>0时,X关于R是粗糙的或不确定的。X关于R越不确定,ρR(X)值越大,粗糙度越大。 大坝系统知识不确定性实质上是其所含信息多少更深层次的刻画[7],故处理其不确定性可嫁接香农信息熵理论[16]。设在由大坝不同年份安全属性集成的非空有限论域U上存在U/ind(R)={R1,…,Ri,…},构造其概率分布矩阵: (5) 式中:p(Ri)=‖Ri‖/‖U‖,表示等价类在U中的概率。 根据式(5),可知知识R的信息熵为: (6) (7) 根据大坝系统DS=(U,R)存在的不确定性,基于粗糙度与粗糙熵所具有的性质,利用粗糙度重新定义粗糙熵[8,10]: CR(X)=C(R)ρR(X) (8) 利用CR(X)来描述大坝系统不确定性,概念上更加清晰,且符合粗糙集逻辑规律,但存在当集合边界不确定性刻画量ρR(X)=0时,CR(X)=0,大坝系统知识不确定性无法表达,故对式(8)进行改进: CR(X)=C(R) [1+ρR(X)] (9) 基于改进粗糙熵计算方法,对大坝系统DS=(U,C∪D,V,f),利用属性相对重要程度进行大坝多源效应量赋权,在利用上式进行粗糙熵计算时,其应表达为:去除某一属性{ci}后的系统不确定性度量,即:CR-{ci}(X)。利用粗糙熵值来表达某一属性对于属性集的绝对重要性,利用下式计算属性相对重要程度,实现大坝多源效应量权重计算: (10) 在这里需要注意的是:βR-{ci}实质上是去除{ci}属性后其余属性的权重,故在上式中包含(‖C‖-1)项。 针对大坝系统,为方便建模融合分析,合理推理大坝服役性态,构建建模流程图如图1所示。 图1 基于改进粗糙熵的大坝服役性态推理流程图Fig.1 Flow chart of dam service behavior reasoning based on improved rough set entropy 本文以文献[17]所述工程实例为研究对象,建立基于改进粗糙熵的大坝系统不确定性度量模型,推理大坝服役性态。该混凝土双曲拱坝最大坝高240 m,为监测大坝服役状况,布设了5条坝体正倒垂线以观测坝体水平位移;在坝顶的6个水准点上,以几何水准法观测坝体垂直位移;在坝体间及坝体与基岩间布设20支测缝计测量裂缝开合度;在坝基及两岸分别布设15和22支渗压计进行渗流监测;在基础灌浆廊道布设3个量水堰监测渗流量;在坝体应力集中处埋设若干应变计组进行局部应力监测,利用该拱坝2004-2011年监测资料进行建模分析。首先,构建大坝系统多源效应量初始赋值表1,并对其进行离散化处理,离散手段同文献[4],建立效应量特征集于表2。 表1 大坝系统多源效应量初始赋值表Tab.1 Initial assignment for dam system multi-effect quantities 注:x1~x8分别为该拱坝2004-2011年每年安全属性;c1~c7为条件属性集,分别为水平位移、垂直位移、接缝开合度、坝基扬压力、渗流量、绕坝渗流和局部应力;d为决策属性集,表示大坝安全状况,表2同。 表2 大坝系统多源效应量特征集Tab.2 The characteristic values of dam system multi-effect quantities 依据前文所述建模实现流程,计算可得:CR-{c1}(X)=CR-{c3}(X)=0.283,CR-{ci}(X)=0.227(2,4,5,7),CR-{c6}(X)=0.452。利用式(10)分别计算属性权重,分别为:βR-{c1}=βR-{c3}=0.024 5,βR-{ci}=0.019 6(i=2,4,5,7),βR-{c0}=0.039 1并结合表1计算得到该坝从2004-2011年安全属性值,与表1决策集进行对比,将结果列于表3。 由表3可以明显看出,基于本文方法所推理的大坝服役性态同已知大坝安全评价等级一致,验证了本文方法的可行性。从表3中还可看出,x5、x7和x8推理所得安全属性值判断大坝在2008、2010和2011年服役性态虽处于正常状态,但其值都略大于0.8,接近基本正常状态。 表3 基于改进粗糙熵的大坝历年服役性态推理Tab.3 Dam service behavior reasoning over the years based on improved rough set entropy 结合具体工程实例,本文基于改进粗糙熵对该坝服役性态进行了合理的推理,验证了所建模型的可行性。利用粗糙集理论,将大坝系统不确定性较为全面的分为集合边界不确定性和知识不确定性,并利用粗糙度和粗糙熵进行度量,避免了单一不确定性方法对系统不确定性刻画不全面问题,并且结合已有研究成果,利用粗糙熵代替信息熵,更加符合粗糙集逻辑。为大坝服役性态合理评价提供了新路径。 □ [1] 何金平.大坝安全监测理论与应用[M].北京:中国水利水电出版社,2010. [2] 施玉群,何金平.基于信息熵的大坝多效应量聚类融合诊断模型[J].水力发电学报,2013,32(5):239-243. [3] 杨露菁,余 华.多源信息融合理论与应用[M]. 北京:北京邮电大学出版社, 2006:7-9. [4] 徐昆振,何金平,夏万求.基于粗糙集与条件信息熵的大坝安全融合评价模型[J].武汉大学学报(工学版), 2014,47(1):46-49. [5] 杨 鹏,杨高升,顾浩威.基于粗糙熵理论的平原河网防洪规划方案评估模型[J].水电能源科学, 2015,33(9):69-73. [6] 李文峰,张金春,金 哲.基于粗糙熵的武器系统效能评估方法研究[J].战术导弹技术,2011,(4):8-11. [7] 苗夺谦,王 珏.粗糙集理论中知识粗糙性与信息熵关系的讨论[J].模式识别与人工智能,1998,(1):34-40. [8] 王向阳,蔡 念,杨 杰,等.基于近似精度和条件信息熵的粗糙集不确定性度量方法[J].上海交通大学学报, 2006,40(7):1 130-1 134. [9] 李 健,史开泉.基于条件粗糙熵的粗集不确定性度量[J].系统工程与电子技术,2008,30(3):473-476. [10] 郑 芳,吴云志.粗集理论中知识的粗糙性研究[J].计算机工程与应用,2002,38(4):98-101. [11] Pawlak Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982,11(5):341-356. [12] Pawlak Z. Rough sets: theoretical aspects of reasoning about data[M]. Kluwer Academic Publishers, 1992. [13] 张文修,吴伟志.粗糙集理论介绍和研究综述[J].模糊系统与数学,2000,14(4):1-12. [14] 王国胤,于 洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766. [15] 李 鸿.一种基于粗糙熵的知识约简算法[J].计算机工程与应用,2005, 41(14):78-80. [16] Shannon C E. A mathematical theory of communication[J]. Bell System Technical Journal,1948,27(3):379-423. [17] 夏万求,何金平.基于粗糙集理论的多效应量融合评价模型及应用[J].水电能源科学,2012,30(8):50-52,66.2 基于改进粗糙熵的大坝系统不确定性度量
2.1 基于粗糙度的大坝系统集合边界不确定性度量
2.2 基于粗糙熵的大坝系统知识不确定性度量
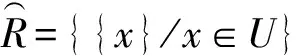
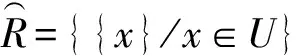
2.3 建立基于改进粗糙熵的大坝系统服役推理模型
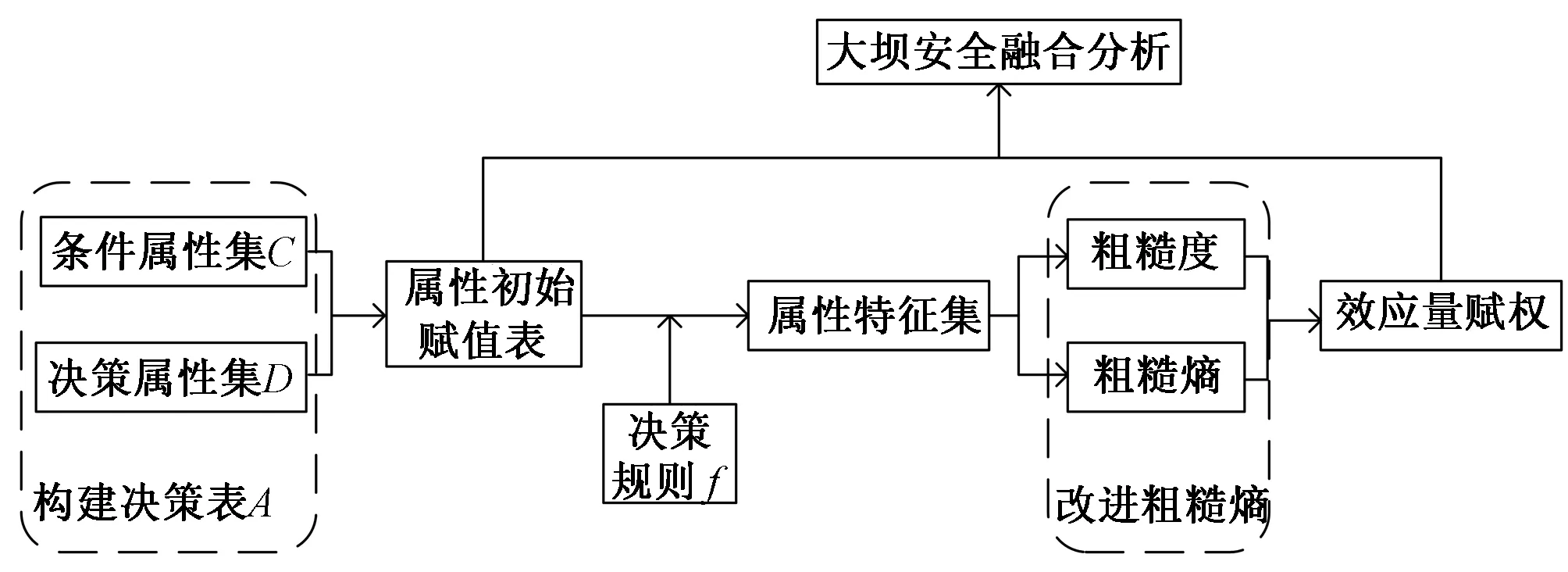
2.4 建模实现流程
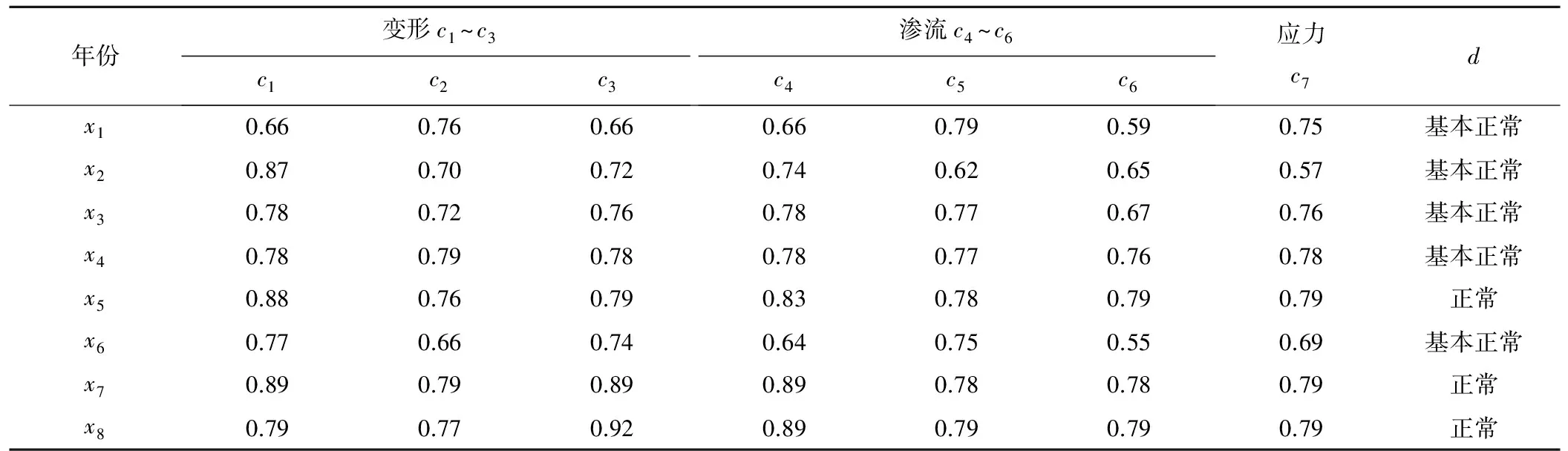
3 实例分析

4 结 语

