投影寻踪法在混凝土热力学参数反演中的应用

宫经伟，唐新军，侍克斌，李双喜，杨力行

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

新疆气候具有严寒、昼夜温差大、年际温差高等特点[1]。随着“丝绸之路经济带核心区”战略的逐步深入，新疆的水利、交通、能源、工业与民用建筑、市政等基础设施建设稳步推进，大量的混凝土结构露置于严寒环境条件下，该环境给混凝土所带来的潜在危害是季节性冻土地区混凝土耐久性方面亟须解决的热点课题[2]。

大量研究表明：低温、昼夜大温差等因素所致混凝土表面形成的较大温度梯度是引起混凝土表面开裂的主要因素，寒区混凝土表现得尤为突出[3]。随着混凝土结构温度场计算理论的日趋成熟和计算机仿真技术的逐步提高，对混凝土结构在各温控措施下的温度场进行仿真计算，以此得到混凝土表面温度梯度，进而确定保温措施是常用的方法。然而，混凝土是热的不良导体，影响混凝土结构温度场仿真计算的因素较多，其中以混凝土热力学参数的影响最为明显。实验室所测试的热力学参数往往与现场混凝土的实际热力学性能有偏差。在实际工程中，根据实测温度值，结合混凝土三维温度场有限元仿真计算技术，采用参数的反演分析是近年来学术界和工程界确定混凝土的热力学参数的有效途径[4]。

随着现代演化算法的逐步发展，近年来，张小飞[5]、李瑞有[6]等采用均匀设计理论、优化算法与温度场三维有限元仿真相结合的方法对大坝混凝土的热力学参数进行反演分析，取得了一定的效果。但有学者[7,8]研究发现，基于均匀设计-神经网络-遗传算法的反演分析方法中，网络模型架构存在很强的经验性。

投影寻踪法[9](Projection Pursuit，简称PP)是一种新兴的EDA多元回归计算方法。近年来，投影寻踪理论以其稳定性和准确性等优点被许多学者应用于水利工程和农业工程等领域[10-13]，但将投影寻踪建模方法结合现代演化算法应用于混凝土热力学参数反演分析中的研究鲜有报道。为此，本文以大尺度混凝土试件温度监测数据为基础，基于均匀设计理论以及混凝土三维温度场仿真计算理论，提出采用投影寻踪建模方法对季节性冻土地区混凝土热力学参数进行反演分析，为混凝土温度应力场的计算提供高精度热力学参数。

1 基本理论

1.1 混凝土温度场计算理论

有热源的均匀、各向同性的固体材料的热传导方程为：

(1)

初始条件：

T(x,y,z,t)=T0(x,y,z),τ=0

(2)

第一类边界条件：

T(τ)=f1(τ),τ>0

(3)

第二类边界条件：

(4)

第三类边界条件：

(5)

式中：τ为时间；a为混凝土的导温系数，m2/h；c为混凝土的比热，kJ/(kg·℃)；ρ为混凝土的密度，kg/m3；λ为导热系数，kJ/(m·h·℃)，λ=acρ；θ为绝热温升，℃；β为表面放热系数，kJ/(m2·h·℃)；Ta为环境温度，℃；n为单位法向量。

1.2 投影寻踪基本理论

投影寻踪是一种用于处理和分析高维试验数据，尤其是非正态、非线性高维数据的新兴统计方法，其优点在于对数据不进行人为假定，具有稳健性好、准确度高、抗干扰性强等特点，文献[14]中有详细阐述，在此不再赘述。设y是因变量，x是p维自变量，PP模型可表示为：

(6)

式中：M、βi、αTi=(αi1,αi1,…,αip)，(‖αi‖=1，i=1, 2,…，M)均为参数；fi(i=1, 2, …，M)是αTix的平滑函数。

2 大尺度混凝土温度监测试验与热力学参数反演分析

混凝土是热的不良导体，在水泥水化热和外界气温的共同作用下，混凝土内部温度分布不均匀，不同部位处的温度变化规律也不尽相同，体现出的热力学性能也有所差异。为了客观反映混凝土内部不同部位处的热力学特性，以确定混凝土的导热系数、不同保温条件下混凝土表面放热系数、混凝土绝热温升、绝热速率等热力学参数，本文选取了距离混凝土结构表面不同距离处多个测点温度作为目标进行反演分析。

2.1 试验方案

试验混凝土配合比如表1所示，大尺度混凝土温度监测试验及具体测点布置如下：大尺度混凝土试件的尺寸为1.5 m×1.5 m×2.0 m(长×宽×高)，为获得不同保温条件下的热力学参数，顶面混凝土裸露在空气中，底面采用钢模板，其余4个面均覆盖10 cm厚保温苯板；如图1所示，测点布置于XY平面上，A1、A2、A3、A4测点分别距离裸露混凝土侧为10、20、50、100 cm；A7、A6、A5、A4测点分别距离覆盖保温苯板侧为10、20、50、75 cm。

表1 混凝土配合比Tab.1 Mix proportions of concrete

2.2 试验过程

(1)采用木质建筑模板使混凝土试件满足图1中的大尺度试件几何尺寸，在典型温度测点处布置横向或纵向细钢筋。

(2)试验采用南京卡尔胜水电科技公司生产的NCT-T系列埋入式铠装铜电阻温度计，将温度计固定于细钢筋上，并将温度计电缆沿细钢筋引出。

(3)进行混凝土浇筑，待振捣后的混凝土完全覆盖电阻式温度计时，开始对各测点温度进行监测。由于铜电阻温度计具有统一的仪器特性参数(0 ℃电阻值为46.60 Ω，电阻温度系数为5 ℃/Ω)，利用铜电阻温度计电阻测值和上述仪器特性参数可方便算出测点的温度。采用此原理，课题组开发了温度自动化监测及分析系统，以此来对试验各测点温度进行连续自动地监测，采集频率设置为2 h，监测时间为120 d。

(4)考虑到浇筑时气温较低(约为8 ℃)，试件浇筑完后7 d拆模，然后按照前述方案中的保温措施进行保温。

2.3 大尺度混凝土热力学参数反演分析

2.3.1 反演分析参数范围确定

采用双曲线模型表征混凝土水化放热过程，如下式所示：

(7)

式中：τ为龄期；n为温升速率。

根据已有研究成果[4]，选取导热系数λ、表面放热系数β、等效表面放热系数(覆盖保温被)β′、绝热温升θ以及温升速率n5个参数作为反演分析参数，其取值范围如表2所示。

2.3.2 训练样本

采用均匀设计理论，按照均匀设计表进行设计，得到30组训练样本，如表3所示；同时按照均匀设计理论生成9组训练样本，用于对建模结果进行检验，检验样本如表4所示。

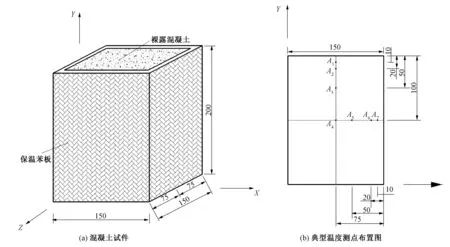
图1 试验布置图(单位：cm)Fig.1 Location of measuring device and arrangement of the concrete specimen

参数λ/(kJ·m-1·d-1·℃-1)β/(kJ·m-2·d-1·℃-1)β′/(kJ·m-2·d-1·℃-1)θ/℃n取值范围120～200300～200020～50025～401．0～3．0

表3 基于均匀设计的30水平训练样本Tab.3 Level of 30 training samples based on uniform design

表4 基于均匀设计的9水平检验样本Tab.4 Level of 9 test samples based on uniform design

2.3.3 热力学参数反演分析

采用课题组开发的混凝土温度场计算子程序，分别将表3和表4中参数代入有限元模型里进行计算，并按下式计算目标函数值：

(8)

式中：i为测点序号，依次代表图1中典型测点A1、A2、A3、A4、A5，A6、A7；Ti(tj)为i测点j时刻计算温度；T*ij为i测点j时刻实测温度。

3 结果与分析

大尺度混凝土试件120 d龄期的温度监测结果如图2所示。依据图2温度监测数据，采用PP建模方法对混凝土热力学参数进行反演分析，分析结果如下：S=0.10，M=3，N=30，P=5，Q=1；函数权重为β=(1.013 7,0.074 2,0.062 2)，投影方向为：

(9)

图2 试验温度监测结果Fig.2 Temperature monitoring results

同时，9水平检验样本实测值与PP建模预报值最大相对误差为-2.6%，合格率100%。据此得出混凝土热力学参数值，如表5所示。将反演分析所得参数作为已知参数代入有限元模型中进行温度场计算，仅列出A1测点实测温度值和计算温度值的历时过程线，如图3所示。

表5 参数反演分析结果Tab.5 Inversion parameters results

图3 测点A1处实测值与计算值对比图Fig.3 Comparison of measured values and calculated values for A1

需要说明的是，由于A1测点距离混凝土试件表面为10 cm，此测点温度受气温影响较大，此测点的温度梯度也较大，这些因素以及网格疏密程度对计算结果均有不同程度的影响，依据PP反演分析方法得出的混凝土热力学参数所得温度计算值与实测值之间会有误差产生，但从长序列监测数据以及计算成果来看，误差基本在2.0 ℃以内，表现出一定的精度。混凝土是热的不良导体，以混凝土内部多测点的温度监测值作为目标，以此进行反演分析所得热力学参数更能客观反映混凝土真实的热力学属性。

4 结 语

(1)本文提出将无假定的投影寻踪建模方法与均匀设计相结合的优化算法用于混凝土热力学参数反演分析中，取得了较为理想的效果。

(2)大尺度混凝土温度监测试验可行性强，同时，设置不同表面覆盖条件，以混凝土内部多测点的温度监测值为目标函数，更能体现混凝土内部温度的时空分布特点，以此进行反演分析所得结果能更真实地反映混凝土热力学性能。

(3)借助投影寻踪方法结合大尺度混凝土温度监测数据确定混凝土热力学参数的方法更可靠，对其他大体积混凝土工程的热力学参数确定有参考价值。

本文提出采用基于均匀设计、投影寻踪算法的方法对混凝土热力学参数进行反演分析。但有待用其他优化算法与本文的方法进行分析与比较，进一步完善本方法在混凝土热力学参数反演分析中的应用。

□

[1] 邓铭江, 于海鸣, 李湘权. 新疆坝工技术进展[J]. 岩土工程学报, 2010,32(11):1 678-1 687.

[2] Burrows R W. The visible and invisible cracking of concrete[M]. 廉慧珍, 覃维祖, 李文伟, 译. 北京: 中国水利水电出版社, 2013.

[3] 杨华全, 李文伟. 水工混凝土研究与应用[M]. 北京:中国水利水电出版社，2005.

[4] 宫经伟. 水工准大体积混凝土分布式光纤温度监测与智能反馈研究[D]. 武汉：武汉大学, 2013.

[5] 张晓飞, 李守义, 陈尧隆, 等. 改进的BP神经网络在碾压混凝土坝温度场反分析中的应用[J]. 西安理工大学学报，2009,(1):95-99.

[6] 李端有, 甘孝清, 周 武. 基于均匀设计及遗传神经网络的大坝力学参数反分析方法[J]. 岩土工程学报，2007,29(1):125-130.

[7] Yu Y Z, Zhang B Y, Yuan H N. An intelligent displacement back-analysis method for earth-rockfill dams[J]. Comp Geotech, 2007,34:423-434.

[8] 向 衍, 苏怀智, 吴中如. 基于大坝安全监测资料的物理力学参数反演[J].水利学报，2004，(8):98-102.

[9] 付 强, 赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.

[10] 付 强, 付 红, 王立坤. 基于加速遗传算法的投影寻踪模型在水质评价中的应用研究[J].地理科学,2003,23(2):236-239.

[11] 郑祖国, 杨力行. 1998年长江三峡年最大洪峰的投影寻踪长期预报与验证[J]新疆农业大学学报,1998,21(4):68-71.

[12] 梁煜峰, 付 建. 投影寻踪法和遗传算法在洪水预报中的应用[J].东北水利水电,2010,28(4):37-40.

[13] 金菊良, 魏一鸣, 丁 晶. 水质综合评价的投影寻踪模型[J].环境科学学报,2001,21(4):431-434.

[14] 李香云, 杨力行. 堡子沟流域农业经济系统投影寻踪回归(PPR)分析[J].新疆农业大学学报,1999,22(2):158-161

[15] 黄 浩, 何建新, 王新忠, 等. 基于投影寻踪回归的河型影响因素分析[J]. 水电能源科学,2010,28(6):83-85.