改进PROMETHEE的城市防洪减灾方案优选模型----以北京市为例

王 征，余顺坤

(华北电力大学经济与管理学院，北京 102206)

城市防洪减灾方案作为解决城市内部洪水、汛期的重要举措越来越受到重视。防洪减灾方案决策作为复杂多属性决策问题，不仅要考虑社会经济、环境问题，还要考虑对水资源的开发、保护和充分利用。由于城市防洪减灾方案决策影响因素多、决策信息存在主观模糊性、评价指标存在补偿问题，导致决策困难。因此，对于城市防洪减灾方案的优选评价非常必要。目前，国内城市防洪减灾方案评价的相关研究较少，黄俊等[1]应用层次分析法的基本决策理论,建立了城市防洪工程方案选择的层次分析模型；吴成国等[2]提出了利用最大信息熵原理构造投影寻踪评价模型中的投影指标函数，并将该耦合模型应用于实际的城市防洪标准方案优选中，得到了较为稳定的结果；唐言明等[3]针对标准集对分析方法(SPA)联系度计算时如何确定差异度系数i的难点，提出了基于集对分析广义联系度函数的复杂系统方案优选模型，能较好表征不同方案不同指标之间的差异情况。可以看出，各种多属性决策方法为多冲突准则方案评价提供了有效的研究框架，然而在当前城市防洪减灾方案决策过程中仍存在许多问题，使得决策精准性降低。本文利用中智集环境下改进的PROMETHEE模型弥补了前述传统多属性决策方法的不足，提高了决策结果的科学、有效性，以期为中国城市防洪减灾优选评价决策提供参考依据。

1 城市防洪减灾方案优选评价指标体系的构建

城市防洪减灾方案优选评价指标体系的构建是方案优选的第一步。指标体系构建的完整程度会直接影响方案优选的准确度。城市防洪减灾方案包含诸多方面，在当前城市政策、经济、城市建设条件下，本文进行了综合考量，构建了包含城建防洪工程、监测预警、抢险救灾、社会基础支持、防洪科普、科技支撑及洪灾管理7个一级指标和18个二级指标的优选评价指标体系，见表1。

表1 城市防洪减灾方案优选评价指标体系

2 基于区间中智集的改进PROMETHEE方法

2.1 备选规划方案识别

本阶段拟进行备选规划方案的筛选。首先由评估专家组成的评审委员会对备选方案集信息进行收集并根据收集信息实施预评估。评审委员会建立备选方案一票否决指标，对不符合规章制度或对自然环境、生态保护、社会有显著影响的方案进行过滤，形成有效备选规划方案集。

2.2 区间中智集定义

设X为一非空集合，x为集合X中的元素，X上的一个区间中智集可以表示为A={TA(x)，IA(x)，FA(x)|x∈X}，其中TA(x)、IA(x)、FA(x)分别表示隶属度、犹豫度、非隶属度，且TA(x)，IA(x)，FA(x)隶属于[0,1]，0≤sup[TA(x)]+sup[IA(x)]+sup[FA(x)]≤3[5]。

设x=([TLx,TUx],[ILx,IUx],[TLx,TUx])和y=([TLy,TUy],[ILy,IUy],[TLy,TUy])是两个区间中智集，则有如下运算规则[6]：

x⊕y=([TLx+TLy-TLxTLy,TUx+TUy-TUxTUy],

[ILxILy,IUxIUy],[FLxFLy,FUxFUy])

(1)

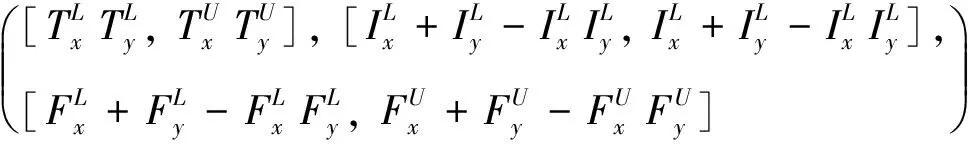
(2)

nx=([1-(1-TLx)n,1-(1-TUx)n],

[(TLx)n,(TLx)n], [(FLx)n,(FLx)n])n>0

(3)

2.3 基于区间中智集的改进PROMETHEE方法

2.3.1 专家群体意见集结

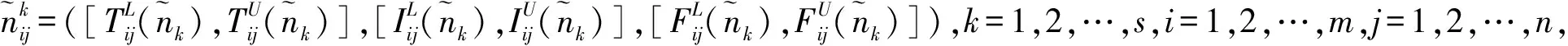
(4)

基于专家信息集结得到的群决策矩阵为：

(5)

2.3.2 基于可能度的优先函数构建

P([ILij,IUij]≥[ILi′j,IUi′j])+P([FLij,FUij]≥(FLi′j,FUi′j])}

(6)

P([TLij,TUij])≥[TLi′j,TUi′j])=

(7)

同理可得P([ILij,IUij]≥[ILi′j,IUi′j])，P([FLij,FUij]≥[FLi′j,FUi′j])。

设p与q分别为严格优于阈值和无差异阈值，基于中智集Nij与Ni′j之间的可能度比较关系，构建方案间关于指标Cj的优先函数y(Nij,Ni′j)：

(8)

优先函数y(Nij,Ni′j)表示中智数得分Nij优于Ni′j的程度。其中，y(Nij,Ni′j)等于1表示方案Ai在指标Cj上的得分Nij强优于和方案Ai′在指标Cj上的得分Ni′j；y(Nij,Ni′j):0.5表示Nij与Ni′j之间的关系为弱优于关系；y(Nij,Ni′j):0表示Nij劣于Ni′j或两者之间无差异。

2.3.3 赋权的级别优先函数构建

(9)

基于赋权的级别优先函数建立方案间的比较关系矩阵如下：

(10)

(12)

3 工程案例

3.1 项目情况

应用本文所建立的城市防洪减灾方案优选模型，选用北京市2015年遭受洪水情况下防洪系统的5个方案集作为本次优选评价防洪方案备选集，下面给出中智集环境下改进的PROMETHEE的优选决策过程及其结果。

3.2 决策过程

(1)计算专家群决策矩阵。在此阶段，由五名专家组成的决策小组分别对各方案的不同指标进行评分，形成专家意见调查表。在此期间，为保证专家评分的独立性，本研究采取背对背的评分方式，经过4轮打分与反馈，各专家的决策意见趋于稳定。在此基础上，通过区间中智集广义加权平均算子[公式(4)]对不同专家的决策信息进行集结，得到专家的群决策信息矩阵，如表2所示。

表2 专家群意见集结

(2)计算赋权的级别优先函数。

步骤一，计算优先函数。在得到专家群决策信息矩阵的基础上，通过公式(6)计算方案间关于不同指标的可能度比较关系。经专家讨论后，确定p与q的值分别为p=0.05，q=0.5。进而利用公式(8)计算优先函数，计算结果如表3所示。

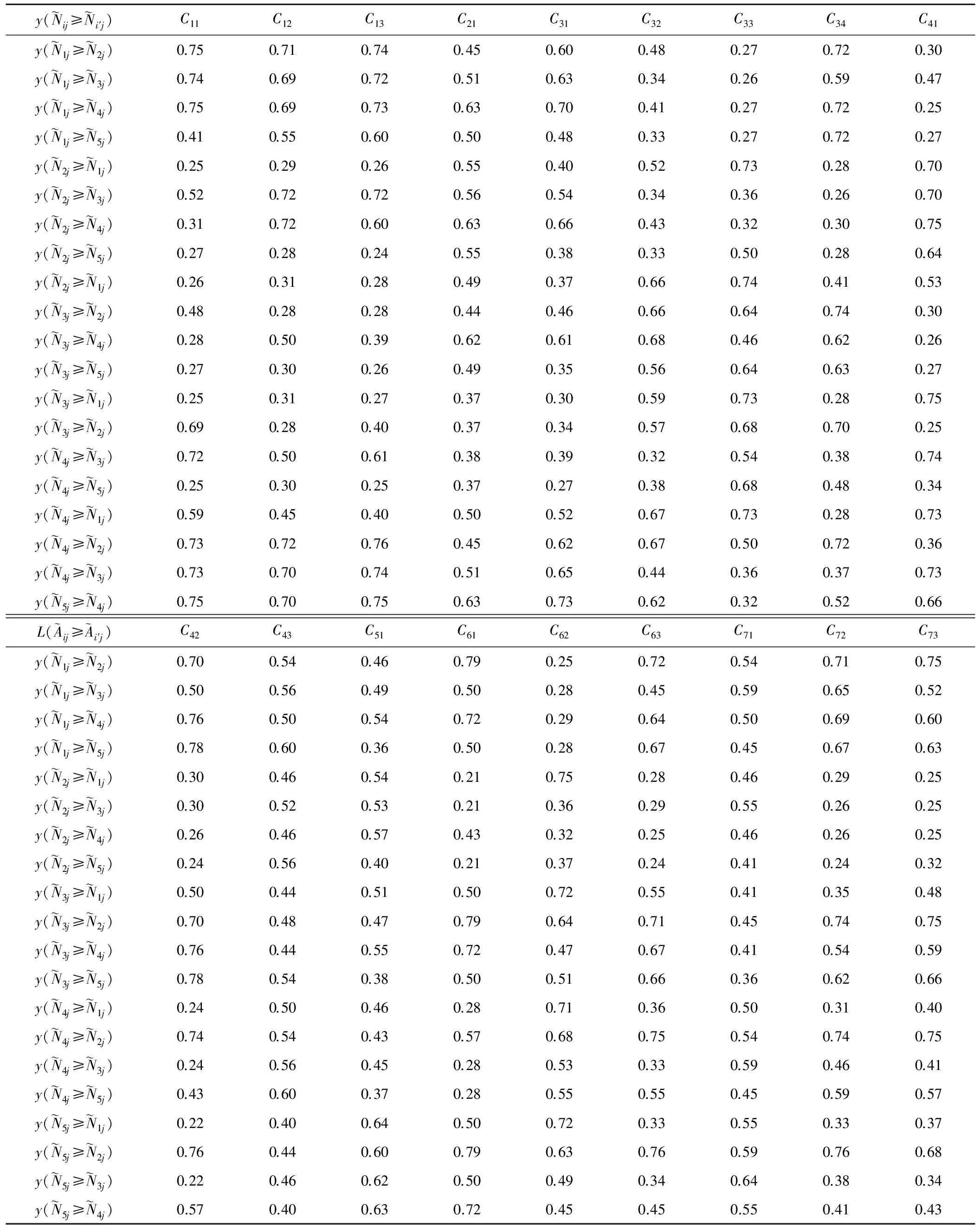
表3 方案比较优先函数计算

步骤二，计算指标权重。专家决策小组对不同指标权重进行独立打分，经过5轮打分与反馈，专家对于指标权重的打分基本趋于稳定。在此基础上利用INULGWA算子对各专家的指标权重信息进行集结，形成指标权重群决策矩阵。

步骤三，计算赋权的级别优先函数。在得到优先函数和指标权重后，利用公式(9)计算赋权的级别优先函数，在此基础上建立方案间的级别优先比较关系矩阵，计算结果如表4所示。

步骤四，计算流入及流出函数。在方案间比较关系矩阵基础上，通过公式(11)及公式(12)计算各个方案的流入及流出函数，计算结果如表5所示。

表4 级别优先比较关系矩阵

表5 流入及流出函数

步骤五，构建方案间的二元比较关系。基于方案地流入及流出比较原则，得到方案间的比较关系排序，为A2>A4>A3>A1>A5。

4 结 语

(1)本文根据城市防洪减灾的实际情况，结合前人的研究成果，综合考虑城市防洪减灾方案评价各个指标影响因素，构建了城市防洪减灾方案评价体系。

(2)结合中智集理论和改进的PROMETHEE法构建了城市防洪减灾方案优选框架，最大化解决了指标间补偿问题及方案之间的排序问题，利用中智集在描述评价结果方面的优势和改进的PROMETHEE方法具有较强实用性的特点，本文在优选过程中为决策存在模糊性和信息不确定等问题提供了可行的解决方法。

(3)本文以北京市为例进行了实证分析，框架的可行性和有效性得以验证，为城市防洪减灾方案决策提供了参考依据。

□

[1] 黄 俊, 付 湘，柯志波. 层次分析法在城市防洪工程方案选择中的应用[J]. 水利与建筑工程学报, 2007,(1):52-55.

[2] 吴成国, 金菊良, 魏一鸣，等. 城市防洪标准方案优选的最大信息熵原理与投影寻踪耦合模型[J]. 中国管理科学, 2008,(S1):1-4.

[3] 唐言明, 白 夏, 卜 松, 等，吴成国. 基于广义联系度函数的城市防洪标准方案优选模型[J]. 水利与建筑工程学报, 2016,(2):178-181.

[4] 刘培德, 李洪刚, 王 鹏，等. 基于区间中智集的ELECTRE方法及其在多属性决策中的应用[J]. 山东财经大学学报, 2016,(2):80-87.

[5] K Govindan, D Kannan, M Shankar. Evaluation of green manufacturing practices using a hybrid MCDM model combining DANP with PROMETHEE[J]. International Journal of Production Research, 2015,53(21):6 344-6 371.

[6] F Samanlioglu, Z Ayag. Fuzzy ANP-based PROMETHEE II approach for evaluation of machine tool alternatives[J]. Journal of Intelligent & Fuzzy Systems, 2016,30(4):2 223-2 235.