提高学生数学应用能力的策略

刘正

新课标指出，要使学生初步学会从数学的角度发现问题和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力。

一、理论联系实际，培养学生的应用能力

数学具有高度的抽象性、严密的逻辑性和应用的广泛性。由于受年龄特点和认识水平的局限，小学生总觉得数学是枯燥的、无味的，远远没有语文科中趣味横生的故事，贴近生活的作文有意思。数学家华罗庚也曾说过，“人们对数学早就产生了干燥无味，神秘难懂的印象，成因之一便是脱离实际。”所以在小学数学教学中要紧密联系学生活实际和他们所熟悉的社会实践，以利于他们理解和掌握抽象的数学知识，把所学的知识与生活实际、社会实践联系起来，解决一些简单的实际问题，达到学以致用的目的。

如在认识常用体积单位时，可让学生从身边去寻找哪些物体的体积接近1立方厘米、1立方分米、1立方米。引导学生认识一节手指头大约1立方厘米，一个粉笔盒大约1立方分米，讲台大约1立方米。又如教学不常用的面积单位“公顷”，因1公顷=10000平方米，引导学生推算，我们的校园的长和宽约100米，校园面积≈100×100=10000平方米，所以1公顷大约相当于我们校园面积的大小。这种结合学生生活实际的教学，使学生对抽象的知识有一个感性的具体认识。

二、加强学具操作，培养学生的应用能力

小学生的思维持点是具体形象思维占优势，他们获取绝大部分数学知识是在形象的感受感知的基础上逐步建立表象，从而形式概念的。因而，教学中加强实际操作十分必要，使学具操作成为学生认知的桥梁。同时也使学生在操作学具中锻炼实践能力。

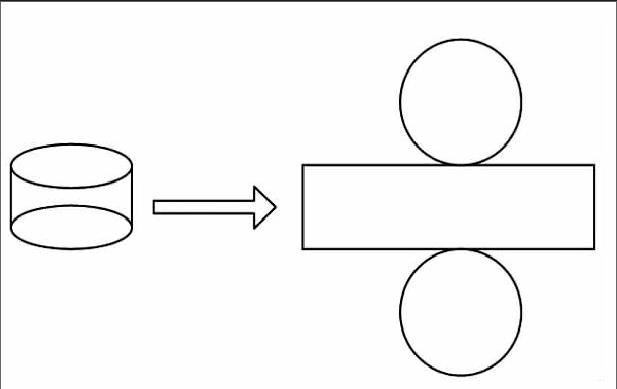
例如，教學圆柱侧面积计算公式，公式本身具有高度的抽象性，教学时，不能仅仅注意公式本身，更重要的是注意公式的形式过程。我在教学中，先让学生拿出课前自制的学具——厚纸片做的圆柱模型，将模形打开如下图：

然后围绕以下问题展开讨论：

（1）圆柱侧面展开后变成什么图形？

（2）展开得到的长方形与圆柱侧面有什么关系？

（3）圆柱的侧面积应怎样计算？

在这个过程中，给学生充裕的时间亲自操作，并通过观察、分析、比较和讨论，发现长方形的长等于圆柱底面周长，长方形的宽等于圆柱的高，从而归纳概括出“圆柱的侧面积=底面周长×高”。在这个过程中，公式完全由学生自己得出。而传统的教法中，往往让学生记住公式，然后把重点放在套用公式计算圆柱的侧面积或表面积上，而忽视了公式的形成过程，把大部分时间放在繁琐的计算上，这不仅不利于学生能力的培养，还浪费了学生的精力和时间。

三、上好实践活动课，培养学生的应用能力

数学实践活动课有别于学习具体知识的探索活动，更有别于课堂上教师的直接讲授，是一类以问题为载体、以学生自主参与为主的学习活动，其教学目标是帮助学生积累数学活动经验、培养学生的应用能力。

案例：教了“比和比例”之后，把学生带到操场上，要求学生测量计算旗杆的高度。如何测量？多数同学摇头，少数窃窃私语：

生a：爬上去量！

生b：爬上去也够不着顶端啊，好危险的！

生c：……

正当同学们议论纷纷的时候，适时取来了一根长1.5米的竹竿，笔直插在球场边。这时阳光灿烂，马上出现了竹竿的影子，量得这影子长1米。

启发学生思考：从竿长是影子的1.5倍，你能想出测旗杆高度的办法吗？

生d：旗杆高也是它的影长的1.5倍。

生e补充：必须要在同一时间内。

这个想法得到肯定后，学生们很快从测量旗杆影子的长，算出了篮球架的高。回到教室后，启发学生用比例写出一个求旗杆高的公式。

这样的实践活动不仅关注结果，更关注学生积累活动经验、展现思考历程、交流收获体会、激发创作潜能的过程，这样的活动形式更利于激发、促进、培养学生的应用意识。

责任编辑韦英哲