圆锥曲线切线的一条性质再探
北京市陈经纶中学 (100020) 张留杰 孙丕训
圆锥曲线切线的一条性质再探
北京市陈经纶中学 (100020) 张留杰 孙丕训
文[1]中结合一道试题探究了过椭圆(双曲线)外一点所引的两条切线的一条性质,并且仅仅局限于焦点在x轴的情况下,我们发现对于焦点在y轴时,相应结论也是正确的,所以可以将文[1]的结论改进如下:
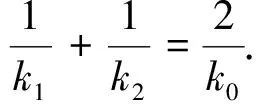
我们发现此优美结论与点M密不可分,即它在曲线W的一条对称轴(y轴)上,如果直线AB与x轴相交于点N,那么k1、k2和直线PN的斜率k′会有何种关系呢?
经过探究,我们得出
结论2 过中心在原点、焦点在坐标轴上的有心圆锥曲线W外一点P引两切线PA、PB,切点弦AB所在直线与x轴交于点N,当直线PA、PB、PN的斜率存在且不为零时,设它们的斜率分别为k1、k2、k′,则k1+k2=2k′.
下面以椭圆为例进行证明,如图1.
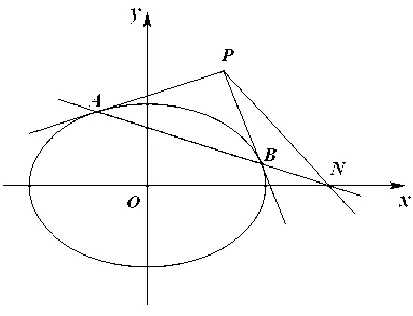
图1
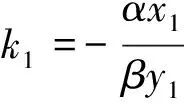
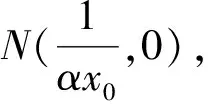
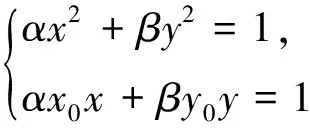
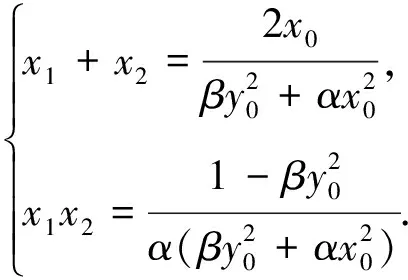
同理,在双曲线中,也不难证明该结论成立.
由结论1和结论2,我们不难得出关于椭圆和双曲线切线的一个性质定理:
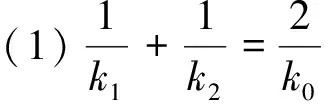
能否将此定理的结论推广到抛物线呢?
由于抛物线可以看作是“另一顶点在无穷远点”的椭圆,所以抛物线的另一条对称轴也可以认为在无穷远处,于是过抛物线外一点引两条切线PA、PB,切点弦AB所在直线与另一条对称轴的交点M(或N)就在无穷远点,所以PM(或PN)应该与AB平行,其斜率k0(或k′)等于直线AB的斜率k.于是我们得出如下定理:
定理2 过顶点在原点的抛物线W外一点P引两条切线PA、PB,切点分别为A、B,直线AB与抛物线的对称轴交于点M,设切线PA、PB的斜率分别为k1、k2,直线AB的斜率为k,直线PM的斜率为k0,当k1、k2、k、k0均不为零时.
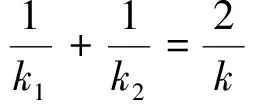
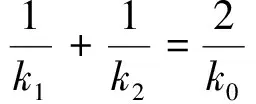
下面以对称轴为x轴的抛物线为例进行证明.
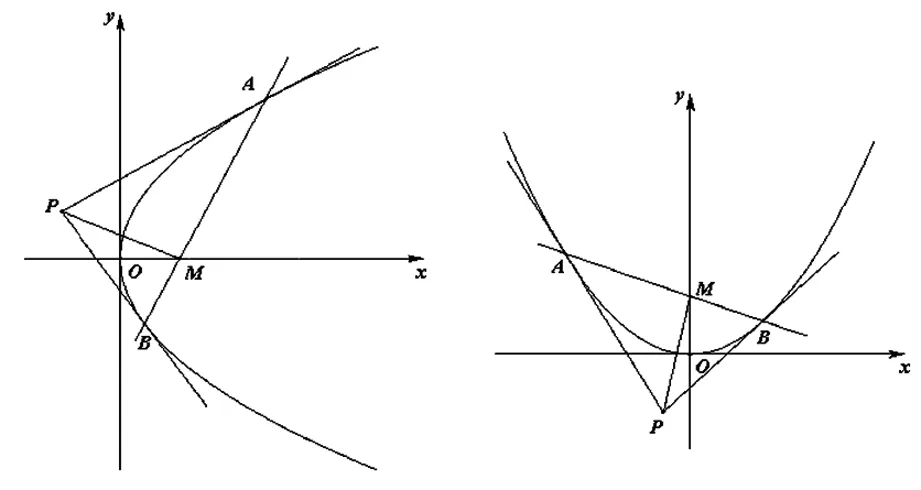
图2 图3
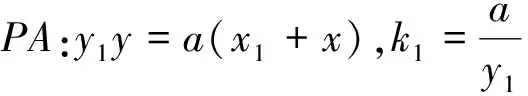
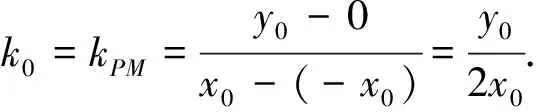
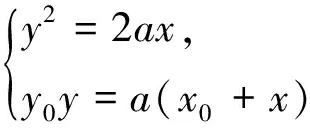
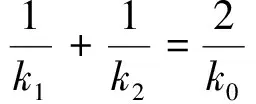
[1]刘宜兵,廖 华.一道高三调研试题的结论推广[J].中学数学研究(江西),2016,7.

