例谈竞赛中的数列问题

安徽省萧县中学(235200) 邱宇 王明坤

例谈竞赛中的数列问题

安徽省萧县中学(235200) 邱宇 王明坤

数列是高中阶段的基础知识也是我们学习的重要内容,在高考及竞赛中也有足够的分量,甚至在大学中还要继续学习数列,怎么提高解题能力呢?下面从4个竞赛试题来研究数列的相关知识.

一、并驾齐驱找主驾——两个数列的复合问题

例1. (2016年浙江省高中数学竞赛试题)已知数列{an}、{bn}满足a1=-1,b1=2,an+1=-bn, bn+1=2an-3bn(n∈N∗),则b2015+b2016=___.

思路: 本题是两个数列的复合,仔细观察要求的结果必然和数列{bn}有关,这就提示我们看能不能求出{bn}的通项,另外2015和2016相差1,或者第二种思路就是采用整体的思想求出{bn+1+bn}的通项.

解: 因为bn+1=2an-3bn,所以bn+2=2an+1-3bn+1,

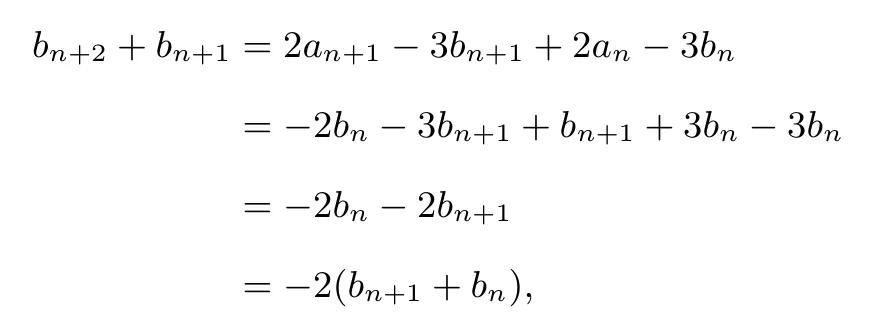
故 {bn+1+bn}可看作公比为 -2的等比数列.从而bn+2+bn+1=(-2)n(b2+b1),注意到b2=2a1-3b1=-8,所以b2015+b2016=(-2)2014×(-6)=-3×22015.

评析: 本题的就是要先消去an,根据条件即可得到只含bn的式子,运用转化的数学思想;然后再把bn+1+bn看作一个整体,运用了整体的数学思想,最后再由一般到特殊即可求解.

二、同根生兄弟一家亲——子数列问题

例2. (2016年全国高中数学联赛江苏赛区初赛试题)已知数列{an}的奇数项依次构成公差为d1的等差数列,偶数项依次构成公差为d2的等差数列,且对任意n∈N∗,都有an＜an+1.若a1=1,a2=2,且数列{an}的前10项和S10=75,则a8=___.

思路: 与例1相比,看起来本题只有一个数列,貌似要简单一些,实则要难,因为一个数列分别有奇偶两个子列,首先n在一般的数列中容易理解,是表示项数,而奇数项和偶数项构成的数列的项数要怎么表示呢,这是一个难点.然后可尝试找出两个数列公差的关系,从两个方面考虑,最后能得到d1=d2,于是问题就变得简单.

由(1)、(2)可知 d1=d2.由 S10=75得 75=5+ 10d1+10+10d2=15+20d1解得d1=d2=3所以a8=a2+3d2=2+3×3=11.

评析: 本题看起来较难打开思路,还是从两个子数列入手,采用分类讨论的数学思想,对于子数列大学中还要进一步学习,这种类型的题目在高考和平时的月考、期末考试中也出现过,因为高考的试卷主要是有大学教授出题目,注重和高中的衔接,要引起我们的重视.另外,因为本题是填空题,不要求写出运算过程,也可以这样考虑: 因为a1=1,a2=2相差不大,两个子数列都是等差数列,并且在整体{an}中始终后项大于前项,从极限逼近的角度来看,只有d1=d2才能符合条件.

三、不解函数,焉得数列——数列与函数的复合

例3. (2016年全国高中数学联赛湖北省预赛试题)已知定义在R上的f(x)满足:且对任意实数x,y,恒有f(x)f(y)=f(x+y)+f(x-y),若数列{an}满足an=3f(n)-f(n-1),n∈N∗

(1)求数列{an}的通项公式;

(2)令bn=是数列{bn}的前n项和,求证Sn＜1.

思路: 本题是数列与函数的复合,要求出{an}的通项公式,根据an与函数的关系,再观察条件,先要把an+1表示出来,恰好得出{an}是等比数列,从而第(1)小题解决问题.第(2)小题求Sn,因为{bn}是复合数列,一般采用放缩、裂项的方法.

评析: 本题是竞赛试题的大题,第(1)小题难度中等,条件要向结论慢慢靠近,两次取特殊值,把f(n+1)表示出来,再凑成条件,即解决问题.运用了由特殊到一般的数学思想.第(2)小题难度偏大,光不等式变形就难以下手,这一难关过去,后面的步骤理解就容易些.其实放缩也就是从一般到特殊的数学思想.

四、上阵父子兵,父亲讲奉献——数列与和的复合问题

例4. (2013年全国高中数学联赛吉林省预赛试题)已知数列{an}的前n项和为Sn,且满足:cn=anbn.

(1)求数列{an}的通项公式;

(2)若2bn-bn-1=0(n≥2,n∈N∗),求数列{cn}的前n项和Tn;

(3)是否存在整数m,M,使得m＜Tn＜M对任意正整数n恒成立,且M-m=4?说明理由.

思路: 在式子中既有an,又有Sn,可把二者形如父子,第(1)小题要求通项,一般要把Sn消去即可,可以用到Sn-Sn-1=an,然后在得到的式子中想法求出an.第(2)小题类型比较常见,是等差和等比的复合数列.第(3)小题考虑利用不等式去解.

所以Tn+1≥Tn=1.故存在整数M=4,m=0.

评析: 此题第(1)、(2)小题采用常规数学思维方法即可,第(3)小题两次利用不等式,难度较大,一般同学不易想到,在以后的学习中,要强化经常用到的不等式思想,使同学们能顺利解决问题.

竞赛中出现的数列问题要引起同学们的重视,在高考中数列的问题也可采用类似的解题技巧.在学习中,要善于归纳、总结,找到解决问题的好办法,逐步提高中学数学的核心素养.