正弦扫频试验振动台与负载界面力获取方法*

张 忠， 张正平， 李海波， 任 方， 韩 丽

(北京强度环境研究所可靠性与环境工程技术重点实验室 北京，100076)

正弦扫频试验振动台与负载界面力获取方法*

张 忠， 张正平， 李海波， 任 方， 韩 丽

(北京强度环境研究所可靠性与环境工程技术重点实验室 北京，100076)

针对传统的基于加速度控制的振动试验中极易出现的“过试验”现象，结合振动台结构动力学和电磁动力学方程，建立了振动台系统的机电耦合模型，获得了振动台输入电流、电压与界面力的映射关系，并通过试验验证了该方法给出的界面力结果与直接测力结果吻合较好，精度满足工程要求。界面力获取方法实施较为方便，与传统振动试验相比，无需改变界面条件，可作为力测量设备直接测力法的有益补充。

振动台机电耦合模型； 界面力； 正弦扫频振动试验； 力限

引 言

在航天飞行器验证和鉴定试验过程中，振动试验起着至关重要的作用[1-2]。在传统振动试验中，工程上都是采用加速度控制的方法，但是由于试验振动台的机械阻抗与星箭对接面的阻抗存在很大的差异,导致利用加速度作为控制曲线会在反共振点处产生严重的“过试验”现象。为了解决系统级及大部件在振动试验过程中出现的“过试验”问题，一般采取关键点响应限幅控制或主动(手动)带谷的方法，这种方法需要根据试验现场测试情况人为地调整试验条件，具有很大的保守性，因而地面模拟试验的有效性有时得不到保证[3]。目前，NASA、欧空局均采用力限控制试验技术来缓解“过试验”现象[4-6]。

力限控制振动试验技术是在传统加速度控制振动试验技术的基础上，引入力响应限幅控制技术，试验中要求夹具与试验件界面同时满足加速度试验条件和力响应限幅控制条件[7]。界面力的获取是力限振动试验实施的基础，一般是在试验件与夹具结构界面间串入力测量设备(force measurement devices，简称FMD)来直接获取界面力[8]。这种方式测量精度较高，但也存在一定的局限性：a.串入的力传感器需施加一定的预紧力，导致传感器的灵敏度发生改变，需要进行复杂的现场标定工作[4]，即使采用预载型传感器，对测力平台的设计和制造工艺要求也较高；b.与传统振动试验方法相比，需在试验件与夹具之间串入力测量设备，这样会破坏结构的刚度连续性[9]。

目前，对于大型航天器系统级动力学环境试验，主要采用噪声试验模拟随机振动环境，采用正弦扫频试验模拟低频瞬态环境。笔者主要开展正弦扫频试验下负载与振动台界面动态力试验获取方法研究，通过建立振动台系统的机电耦合模型获得了界面力和电流电压的映射关系，并通过试验验证了方法的有效性。笔者研究的界面力获取方法实施较为方便，与传统振动试验相比，无需改变界面条件，可作为力测量设备直接测力法的有益补充。

1 振动台系统机电耦合建模

图1为振动台结构示意图。航天产品正弦扫频振动试验关注的频段为5～100 Hz，在此频段下可认为动圈与台面组合体为刚体。根据振动台的示意图可将振动台简化为二自由度系统，在低频段内建立振动台结构的动力学方程为

(1)

其中：ma为动圈和台面组合体的刚体质量；mb为振动台静圈的刚体质量；ka，kb为板簧和空气弹簧的刚度；ca，cb为板簧和空气弹簧的阻尼；f为电磁力。

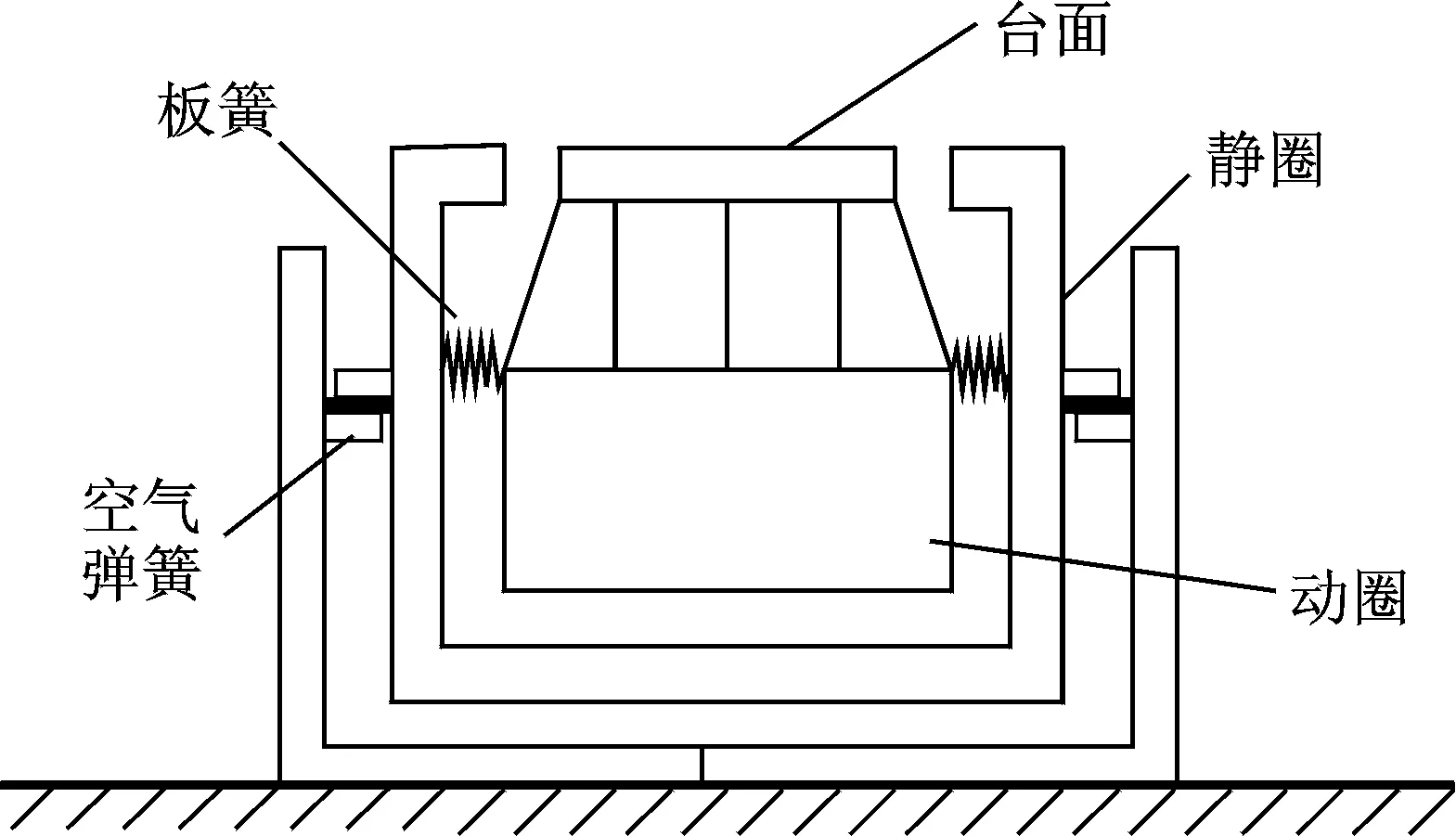
图1 振动台结构示意图Fig.1 Structure diagram of shaker

电磁力满足下式[10]

f=BlnI=KfI

(2)

其中：B为磁场强度；l为单匝线圈的长度；n为线圈匝数；I为输入的电流。

振动台驱动线圈的电流、电压的动力学方程为

(3)

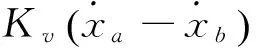
联立式(1)和(3)可得振动台的机电耦合模型为

(4)

文献[11-12]对振动台系统的模态特征进行了研究，分析认为振动台在工作频段外的低频段存在隔振模态。由于隔振模态的特征频率远低于工作频段，可以忽略隔振空气弹簧的影响。经过简化后得到的振动台机电耦合系统模型为

(5)

空台状态下，振动台系统动力学方程的频域形式可以写为

(6)

根据式(6)，振动台的导纳为

(7)

下面分析振动台系统负载情况下的动力学方程。在振动试验状态下，负载结构的动力学方程为

(8)

其中：下标m，s分别代表振动台与负载的界面自由度和非界面自由度；Fm为振动台对负载界面自由度的作用力。

这里需要注意的是，在进行振动试验状态建模时，负载界面仅包含振动台振动方向自由度。

在振动试验状态下，振动台的动力学方程为

(9)

其中：Fa为负载对振动台的反作用力。

考虑交界面的位移和力双协调条件

Xm=Xa

(10a)

Fm+Fa= 0

(10b)

负载状态下振动台的机电耦合系统动力学方程为

(11)

由式(11)的第2行可得

KmsXs+KmmXa-ω2maXa+ jωcaXa+

kaXa-KfI= 0

(12)

由式(8)的第2行可得

KmsXs+KmmXm=Fm

(13)

考虑式(10)中Xm=Xa, 将式(13)代入式(12)，可得

-ω2maXa+ jωcaXa+kaXa=KfI-Fm

(14)

由式(11)的第3行可得

jωKvXa+jωLI+RI=U

(15)

将式(14)代入式(15)，得到

(16)

通过式(7)和式(6)可以看出，振动台的导纳是振动台系统的固有属性，与振动台的机械和电磁学特性相关，即空台状态下的电流与电压之比、负载状态下总电流减去驱动负载所需电流与电压之比，两者是恒定值。

2 基于振动台电流电压的振动台界面力获取方法

振动试验时，负载受到的激励力(即界面力)等于振动台受到的合力减去驱动振动台动圈和台面等刚性质量块所需的力，如图2所示。在电路模拟中，电流正比于力，驱动负载所需的电流等于总电流减去驱动振动台动圈和台面等刚性质量块所需的电流。如图3所示。振动试验时，若已知振动台的输入电压，即可根据振动台的导纳得到驱动动圈和台面等刚性质量所需的电流，进而得到驱动负载运动的电流，最后根据电流与力的关系获得界面力。

图2 振动台力的传递路径Fig.2 Force transfer path of shaker

图3 振动台力传递电路Fig.3 Electro-mechanical analogy of shaker

在频域下通过振动台输入电流电压获得界面力，基本步骤如下。

1) 进行空台正弦扫频振动试验，测量振动台的输入电流Ie、电压Ue等数据，以确定振动台系统的导纳Ye

(17)

2) 安装刚性质量块进行正弦扫频振动试验，质量块质量为m，测量振动台输入电流I和电压U，并测量质量块的加速度响应a，计算Kf

(18)

3) 安装真实试验件进行正弦扫频试验，测量振动台的输入电流I′和电压U′，获得界面力为

Fm=Kf(I′-YeU′)

(19)

需要注意的是，为了消除非线性，刚性质量块的质量最好与真实试验件的质量一致，三次正弦扫频振动试验的量级也应均选取实际试验的量级。

3 试验验证

3.1 负载为刚性质量块的试验验证

为了验证通过电流电压测力方案的正确性，在20t振动台上开展了试验验证。开展空台正弦扫频试验、带525kg质量块的正弦扫频试验、带940kg质量块的正弦扫频试验，三次试验条件一致，试验量级为1.5g，试验条件如图4所示，扫频速度为4 oct/min，然后采集电流和电压等数据。

空台振动试验频域下的电流和电压数据如图5所示。按照式(17)得到振动台的导纳，如图6所示。

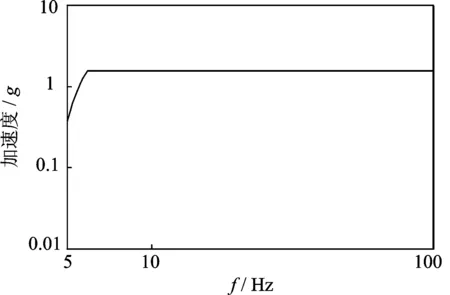
图4 正弦扫频振动试验条件Fig.4 Condition of swept sine vibration test

图5 空台正弦扫频振动试验实测数据Fig.5 Measurement data of swept sine vibration test without load

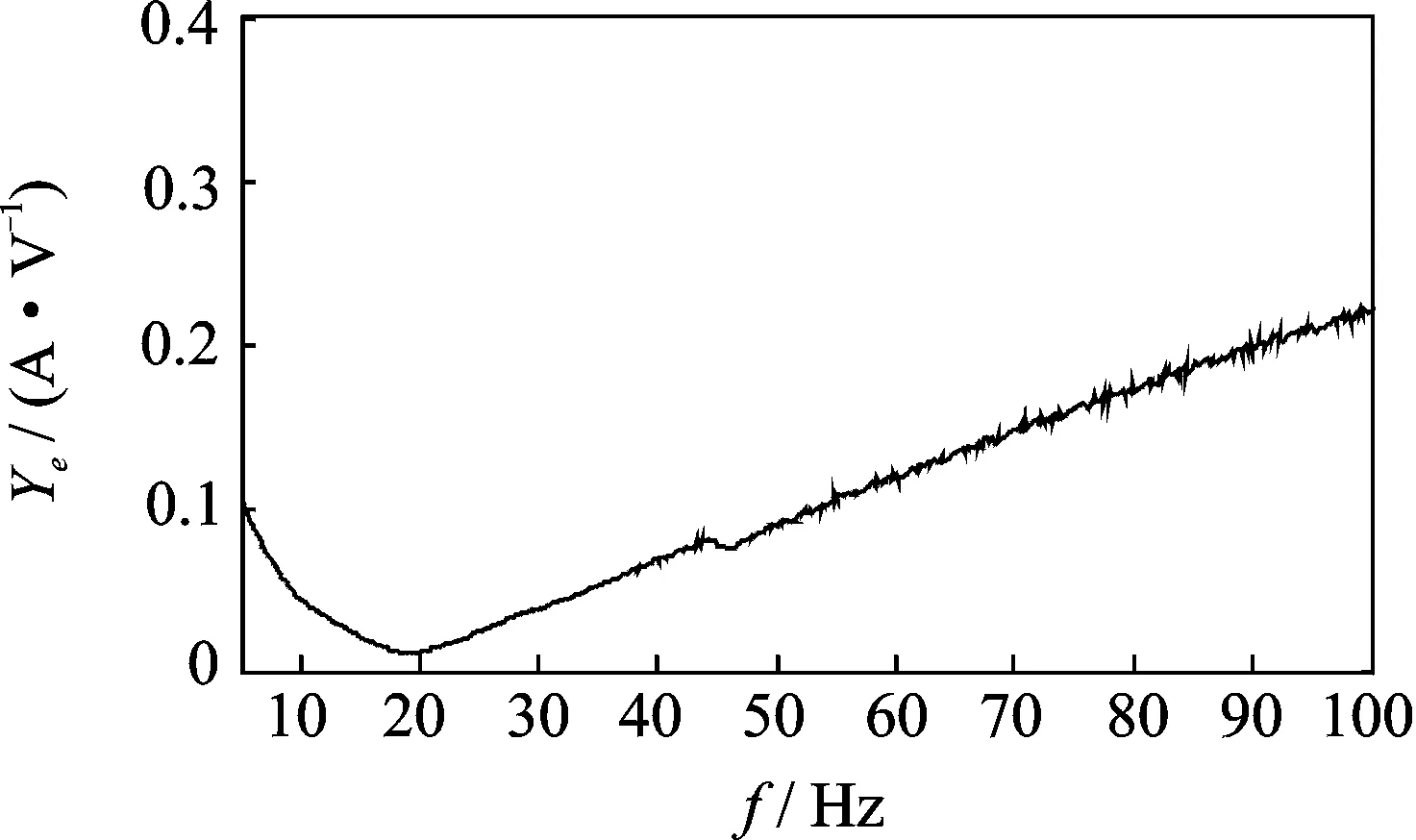
图6 空台导纳幅值Fig.6 Admittance amplitude of shaker without load

开展带525 kg质量块负载的正弦振动试验，按照式获得Kf，计算得到的曲线如图7所示。需要注意的是，振动台磁场受动圈交变电流和运动等因素的影响，导致振动台的Kf随频率变化。因此在频域进行界面力计算时，需采用对应频率点的Kf值。

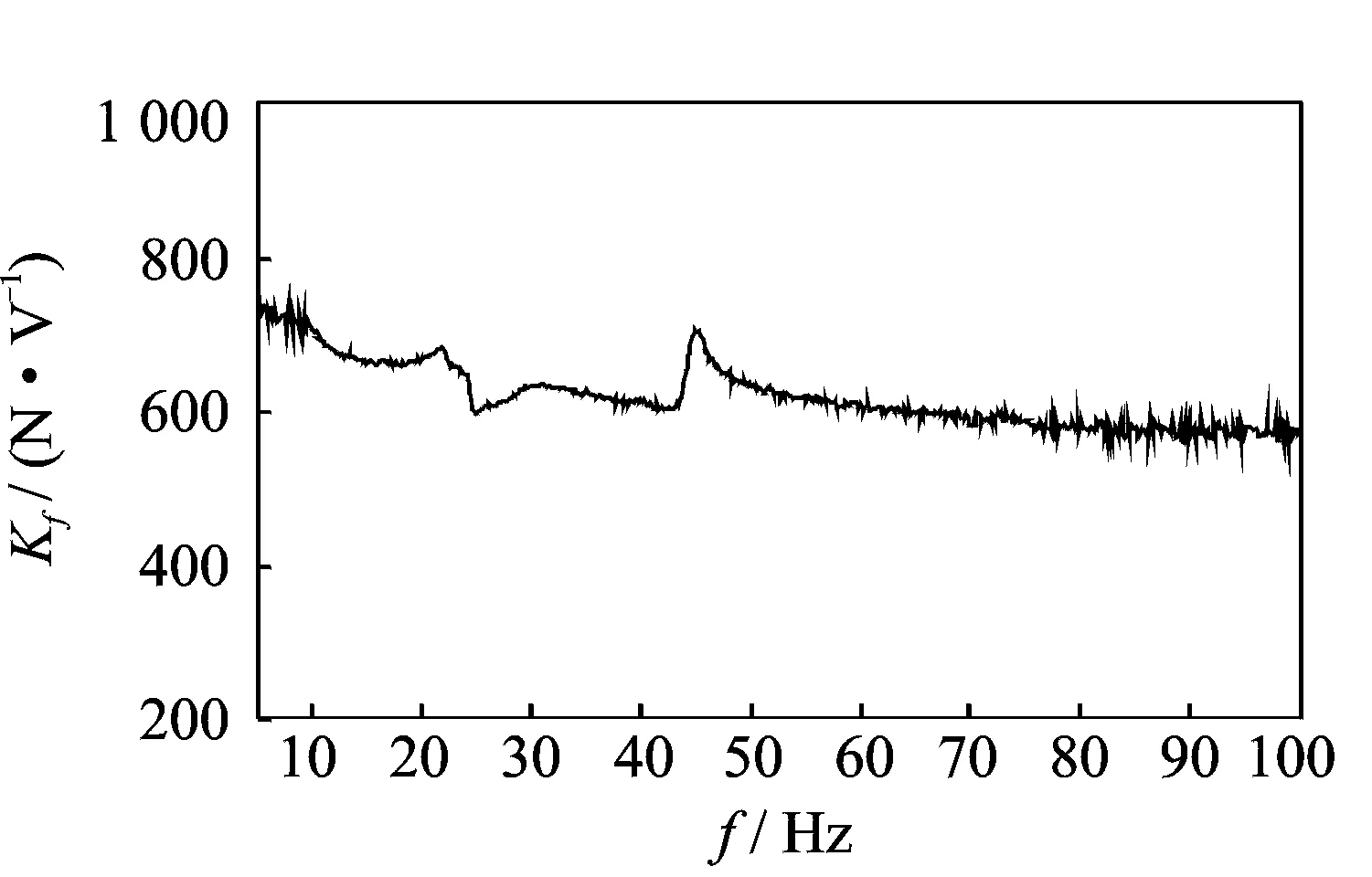
图7 力与电流的比值KfFig.7 The ratio of force and current Kf

最后，开展940 kg质量块的正弦扫频试验获取电流和电压，根据式(18)得到界面力的大小。根据牛顿第二定律Fr=Mrar计算得到力的大小并将其作为参考值，其中：Mr为质量块的质量；ar为实测的质量块加速度。将式(19)计算得到的力与参考值进行比较，如图8所示。可以看出，计算力与参考值的误差小于10%，满足工程要求，这也验证了方法的正确性。

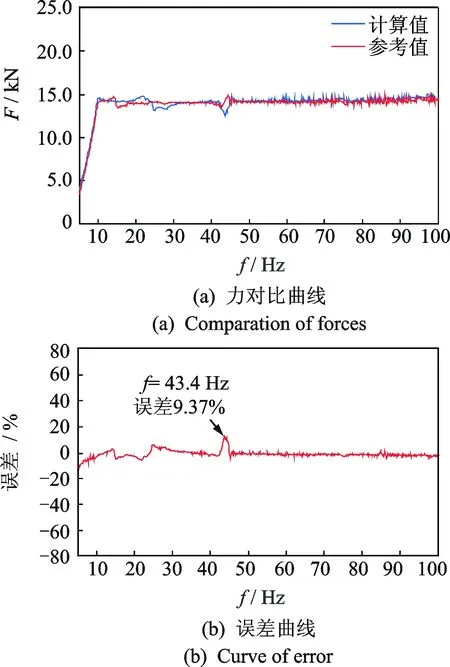
图8 计算值与参考值对比Fig.8 Comparation between calculation and reference value

3.2 负载为真实试验件的试验验证

一般的试验件均为柔性体，为了验证柔性体界面力获取方法，开展了真实试验件的正弦扫频试验。此试验可认为安装夹具的状态为空台状态，即夹具、台面和动圈组成一个刚体质量系统。选取的质量块与真实试件件质量相近，为5 500 kg质量块，如图9所示，上部环形区域为质量块，下部为夹具。

图9 试验夹具与质量块Fig.9 Photo of fixture and mass

试验是在35 t振动台上进行的，分别开展了3个正弦扫频试验，空台状态(含夹具)、刚性质量块状态和真实试验件状态。同上，空台试验用于确定振动台导纳，刚性质量块状态用于确定Kf, 真实试验件状态用于计算界面力。为了验证笔者提出方法的正确性，进行真实试验件振动试验时，在夹具与真实试验件之间串入了力测量设备。基于振动台输入电流电压获取的界面力与力测量设备直接测量得到的界面力对比，如图10所示。

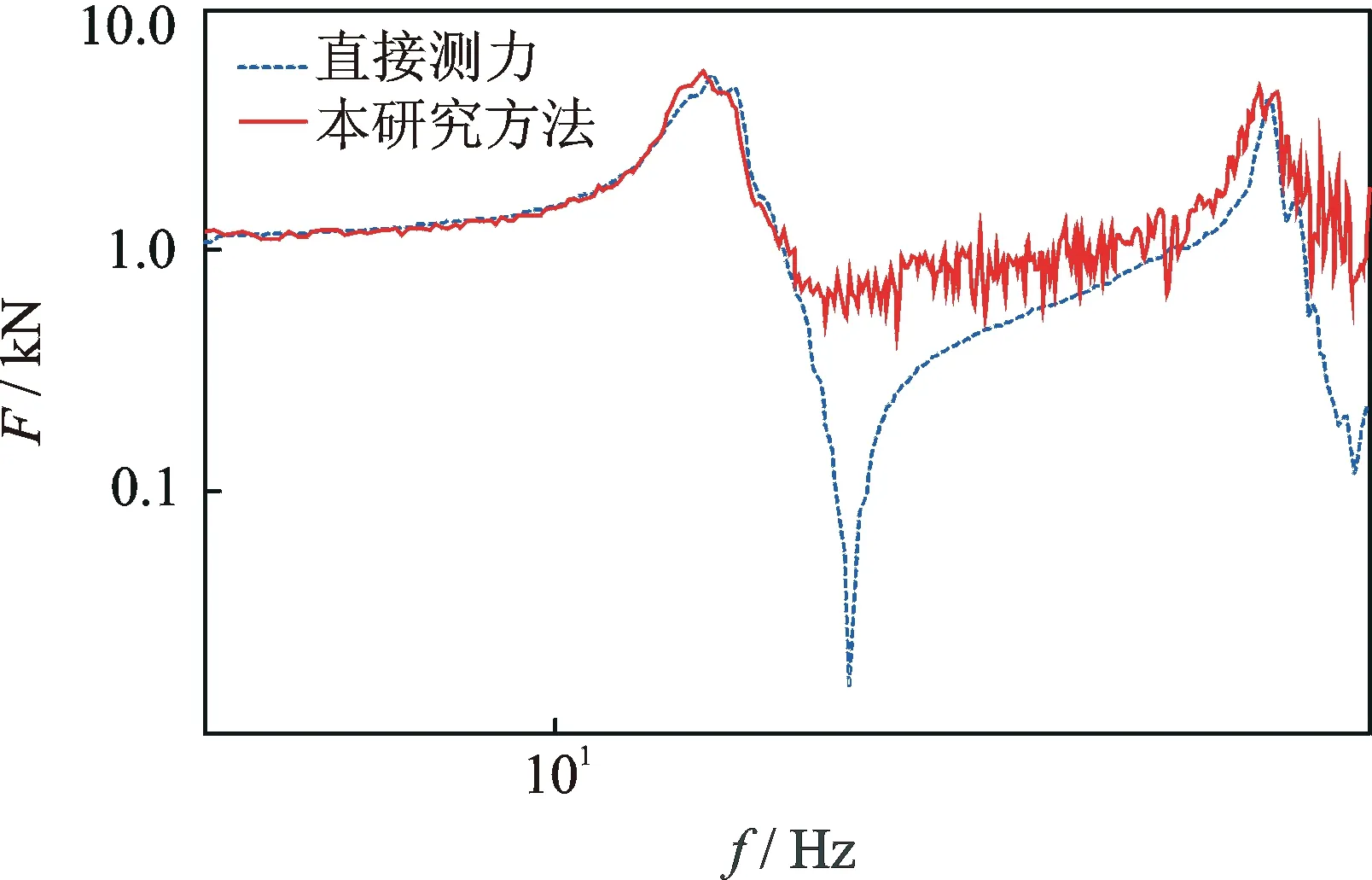
图 10 电流电压间接测力与力传感器直接测力对比Fig.10 Comparation of results obtained by current-voltage of shaker and force transducer

表1 力的峰值误差

Tab.1 Peak error of force

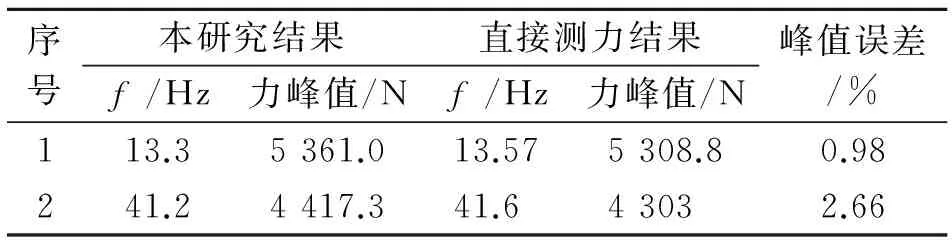
序号本研究结果直接测力结果f/Hz力峰值/Nf/Hz力峰值/N峰值误差/%113.35361.013.575308.80.98241.24417.341.643032.66

从图10和表1可以看出，两者峰值频率和力的峰值吻合较好(反共振点处)。但是在曲线的下凹段存在较大误差，这是由于在进行电流电压测量时存在测量噪声，导致对信号的小值有所掩盖，这种测量误差对力限振动试验的影响可以忽略。因为在力限振动试验中，力是作为限幅引入的，起主要作用的是力的峰值部分，凹谷在力限振动试验时不起作用，笔者提出的方法可以满足工程要求。

4 结束语

力限振动试验可有效缓解传统加速度控制中存在的“过试验”现象，而界面力的获取是力限振动试验实施的基础。笔者给出了一种正弦扫频振动试验的负载/振动台界面力间接获取方法，经过试验验证本方法给出的界面力结果与直接测力结果吻合较好，精度满足工程要求。该方法操作简单且无需改变试验件的安装状态，具有较好的工程应用价值，可为航天飞行器力限振动试验技术提供重要支撑。

[1] NASA-HDBK-7005. Dynamic environmental criteria[S]. Washington: NASA Technical Publication, 2001.

[2] 陈章位, 文祥, 周建川, 等. 力限控制在振动试验中的应用研究[J]. 振动与冲击, 2013, 32(6): 105-108.

Chen Zhangwei, Wen Xiang, Zhou Jianchuan, et al. Application of force limited control in vibration test[J]. Journal of Vibration and Shock, 2013, 32(6): 105-108.(in Chinese)

[3] Marchand P, Singhal R. Evaluation of the force limited vibration semi-empirical constant for a two-degree-of-freedom system[J]. AIAA Journal, 2010, 48(6):1251-1256.

[4] NASA-HDBK-7004C. Force limited vibration testing[S]. Washington: NASA Technical Publication, 2012.

[5] NASA-HDBK-7008. Spacecraft dynamic environments testing [S]. Washington: NASA Technical Publication, 2014.

[6] ECSS-E-HB-32-26A. Spacecraft mechanical loads analysis handbook[S]. Noordwijk: ESA-ESTEC Requirements & Standards Division, 2013.

[7] NASA-RP-1403. Force limited vibration testing monograph[R]. Washington: NASA Reference Publication, 1997.

[8] 李新明, 岳志勇, 张俊刚. 新型力限三向FMD的设计[J]. 航天器环境工程, 2011, 28(3): 251-254.

Li Xinming, Yue Zhiyong, Zhang Jungang. Design of a new type three dimensional FMD for force limited studies[J]. Spacecraft Environment Engineering, 2011, 28(3): 251-254.(in Chinese)

[9] Laine B, Salvignol J C, Ngan I, et al. Force limited vibration testing of JWST NIRSpec instrument using strain gages[C]∥Space Simulation Conference. Annapolis, USA: [s. n.], 2010.

[10]杨毅青，龚继文. 基于电磁感应原理的薄壁件铣削振动抑制[J]. 振动、测试与诊断，2015, 35(3): 429-433.

Yang Yiqing, Gong Jiwen. Milling vibration suppression of thin-walled structure based on electromagnetic induction[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 429-433.(in Chinese)

[11]刘源，董立珉，孔宪仁，等. 飞行器虚拟振动试验平台构建[J]. 光学精密工程, 2013, 21(5): 1258-1264.

Liu Yuan, Dong Limin, Kong Xianren,et al. Construction of virtual vibration testing platform for spacecraft[J]. Optics and Precision Engineering, 2013, 21(5): 1258-1264. (in Chinese)

[12]Ricci S, Peeters B, Fetter R, et al. Virtual shaker testing for predicting and improving vibration test performance[C]∥Proceedings of the IMAC-XXVII. Florida,USA: [s. n.], 2009: 1-16.

10.16450/j.cnki.issn.1004-6801.2017.01.025

*国家自然科学基金资助项目(11502023)

2016-03-21；

2016-06-14

V416.5； TH823

张忠，男，1983年3月生，博士、高级工程师。主要研究方向为结构动力学和振动试验技术。曾发表《动态子结构方法在全箭动特性分析中的应用研究》(《载人航天》2014年第20卷第3期)等论文。 E-mail: zhangzhong8866@163.com