微振动测试平台及其标定方法*
陈江攀, 程 伟, 董家俊, 李 名
(北京航空航天大学航空科学与工程学院 北京,100191)
微振动测试平台及其标定方法*
陈江攀, 程 伟, 董家俊, 李 名
(北京航空航天大学航空科学与工程学院 北京,100191)
由于航天器在轨运行时产生的微振动会对其成像质量和指向精度等关键工作性能产生较大影响,通过地面试验测试航天器各活动部件的微振动特性对航天器的减振/隔振设计至关重要,为此研制了两种微振动测试平台:应变式微振动测试平台(strain micro-vibrations testing platform,简称SMTP)和压电式微振动测试平台(piezoelectric micro-vibrations testing platform,简称PMTP)。为了获得高精度的测试结果,分别针对SMTP和PMTP开发了高精度的标定方法,并通过试验测试对两种测试平台的工作性能进行检验。结果表明,SMTP和PMTP的测试误差分别在±1.10%和±4.94%以内,且二者对同一微振动的振动幅值的测试误差在±4.36%以内。
微振动; 应变式微振动测试平台; 压电式微振动测试平台; 标定方法; 测试误差
引 言
航天器的活动部件在轨工作时产生的振动具有振动幅值低、振动频率小于1 kHz的特性,这类振动通常被称为微振动[1]。活动部件的微振动会对航天器的成像质量和指向精度等关键性能产生较大影响。航天器上存在较多的活动部件,如动量轮、控制力矩陀螺、太阳翼驱动机构、数传天线、制冷机以及相机快门组件等[2-5]。因此,通过地面试验测试各活动部件的微振动特性对航天器的减振/隔振设计至关重要。
近年来,国内外学者对动量轮和控制力矩陀螺的微振动特性进行了大量研究,并取得了大量研究成果。动量轮和控制力矩陀螺的微振动处于中高频区,然而随着高轨遥感卫星的发展,相机的曝光时间显著延长,其工作性能对太阳翼驱动机构驱动真实太阳翼和相机快门组件等在轨运行时产生的低频微振动更为敏感,低频微振动也成为热门研究对象。因此,开发一套全频段的微振动测试设备十分必要。应变式力传感器和压电式力传感器广泛应用于测力领域。应变式力传感器多用于静态力(0 Hz)测试领域,基于应变式力传感器研制的测试平台适用于中低频区微振动的测试。压电式力传感器具有高灵敏度、高分辨率、宽频响和宽测试范围等优点,多用于动态力测试领域[6]。近年来,国内外学者对动量轮和控制力矩陀螺微振动特性的测试使用的都是由瑞士Kistler公司研发的基于压电式力传感器的压电式微振动测试平台[7-12]。然而,由于电荷泄露,压电式力传感器在低频区的工作性能较差[6],因此基于压电式力传感器研制的测试平台适用于中高频区微振动的测试。
为了实现全频段微振动的测试,笔者分别基于应变式力传感器和压电式力传感器研制了两种微振动测试平台,即SMTP和PMTP。为了获得高精度的测试结果,针对两种测试平台分别开发了高精度的标定方法,并通过试验测试对两种测试平台的工作性能进行了检验。
1 工作原理
当被测活动部件安装在微振动测试平台上工作时,活动部件产生的微振动以空间正交的3个力(Fx,Fy和Fz)和3个力矩(Mx,My和Mz)的形式作用在活动部件与测试平台安装平面的等效中心点,测试平台的任务就是实现对6个分量的动态测试。图1为SMTP和PMTP的实物照片。由图1可知,SMTP和PMTP的接口灵活,其内部是一个空腔,被测活动部件既可以安装在测试平台内部,又可以安装在测试平台外部,适用于多种活动部件微振动特性的测试试验,克服了Kistler压电式微振动测试平台接口不够灵活的缺点。

图1 SMTP和PMTP照片Fig.1 Pictures of SMTP and PMTP
1.1 SMTP工作原理
SMTP主要由8个双孔梁应变式力传感器(S1~S8)和负载盘组成,图2为其内部示意图。双孔梁应变式力传感器具有结构刚度高、灵敏度高、稳定性好以及滞后小等优点,广泛应用于称重领域[13-14]。此外,为了结构对称和便于安装,S1~S4均为一个双孔梁,S5~S8由两个双孔梁组成,如图2所示。图3为双孔梁应变式力传感器上应变片的粘贴位置。
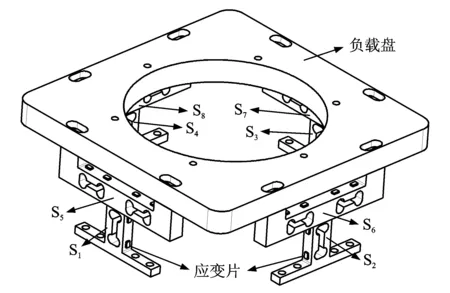
图2 SMTP内部示意图Fig.2 Inner sketch of SMTP

图3 应变片粘贴位置示意图Fig.3 Schematic of the pasting location of strain gauge
如图2和图3所示,竖直双孔梁力传感器S1~S4在4个半圆孔对应的平面上粘贴应变片,即应变片A~D;水平双孔梁力传感器S5~S8只在靠近负载盘的4个半圆孔对应的平面上粘贴应变片,即应变片E~H。每个双孔梁力传感器上的4片应变片组成一个等臂对称全桥电路,其中:应变片A和C接入相对桥臂,应变片B和D则接入该全桥电路的另一对相对桥臂;应变片E和H接入相对桥臂,应变片F和G则接入该全桥电路另一对相对桥臂。双孔梁力传感器S1~S4负责测试Fx,Fy和Mz3个分量,双孔梁力传感器S5~S8负责测试Fz,Mx和My3个分量。因此,SMTP可实现对6个微振动分量的动态测试。
1.2 PMTP工作原理
PMTP主要由8个单向的压电式力传感器(S1~S8)和负载盘组成,图4为其内部示意图。8个压电式力传感器均由4片P5H压电陶瓷片并联组成,以提高PMTP的信噪比。图5为压电式力传感器的结构示意图。
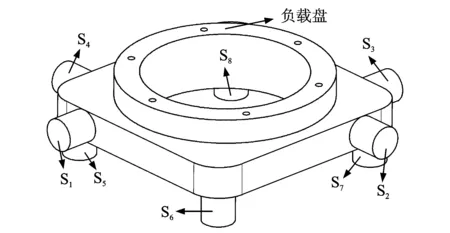
图4 PMTP内部示意图Fig.4 Inner sketch of PMTP
如图4所示,压电式力传感器的一端与负载盘连接,另一端则与固定底座连接。由于PMTP所使用的P5H压电陶瓷片的极化方向为沿压电片的拉压方向,因此压电式力传感器S1~S4负责测试Fx,Fy和Mz3个分量,压电式力传感器S5~S8负责测试Fz,Mx和My3个分量。因此,PMTP可实现对6个微振动分量的动态测试。
2 标定方法
当被测活动部件安装在测试平台上工作时,活动部件所产生的微振动会以6分量扰振力/力矩(Fx,Fy,Fz,Mx,My和Mz)的形式作用在活动部件与测试平台安装平面的等效中心点,此时测试平台的8个单向力传感器将会有8个电压信号输出,标定过程的目的就是确定 8个电压信号和6分量扰振力/力矩之间的转换关系,该转换关系是一个矩阵,称为标定矩阵W。获得了测试平台的标定矩阵W后,6分量扰振力/力矩与8个电压信号之间的转换关系为
F6×1=W6×8U8×1
(1)
标定过程是通过对测试平台的等效中心点施加已知的6分量力/力矩激励并对8个输出电压信号进行测试来实现的。等效中心点是被测活动部件与测试平台安装平面的几何中心点。然而,在此中心点直接施加已知的6分量力/力矩难以实现。为了解决这一问题,笔者在测试平台上安装了一个刚度很高的标定装置,如图6所示。根据空间力系简化原理可知,对图6所示的标定装置的12个加载点施加单向已知力,可简化出作用在等效中心点已知的6分量力/力矩[15]。图6中,O为等效中心点;Lx,Ly和Lz分别为加载点到等效中心点O的力臂,且三者均为0.09 m。

图6 标定装置示意图Fig.6 Schematic diagram of the calibration device
标定过程中,按照图6所示加载点的顺序依次对标定装置施加单向已知力,共12个,记为F′。根据空间力系简化原理可知,将F′简化至等效中心点O需乘以一个转换矩阵C,则F′和C的表达式分别为
简化至等效中心点O的已知6分量力/力矩F的表达式为
(4)
将式(4)代入式(1),可得
(5)
将式(5)两端同时右乘矩阵U的转置矩阵UT,可得
(6)
由于UUT为一个满秩矩阵,将式(6)两端同时右乘它的逆矩阵可得
(7)
其中:W为测试平台的标定矩阵;矩阵C和F′为已知矩阵;矩阵U可通过数据采集系统测试获得。
2.1 SMTP标定方法
SMTP的标定过程是在时域上完成的,它是通过特定的加载装置对标定装置施加已知的阶跃载荷来实现。加载装置由磁力座、两根铝梁、双轴平移台、滑轮、细线以及砝码组成,图7为其实物照片。

图7 加载装置照片Fig.7 Picture of the loading device
该加载装置的作用是将砝码的重力通过细线垂直地施加在标定装置的某个加载点上,待砝码停止摆动后,将细线突然烧断则会对该加载点施加一个阶跃载荷。其中:磁力座的作用是将加载装置固定在刚性底台上;双轴平移台的作用是对细线与加载点所处平面的夹角进行微调,以保证二者垂直;滑轮的作用是减小摩擦。
在标定过程中,对标定装置施加的12个单向已知力均为阶跃载荷,则式(7)中的矩阵F′可写为
(8)
其中:G为砝码及其附属装置的重力。
在阶跃载荷的作用下,SMTP的8个力传感器的输出电压为阶跃信号。将标定过程中SMTP在12个已知阶跃载荷作用下输出电压的阶跃幅值记为Uij,其中:i=1,2, …,8,为8个单向力传感器的编号;j=1,2, …,12,为标定装置12个加载点的编号。Uij的物理意义为:在标定装置的第j个加载点上施加已知阶跃载荷时,SMTP第i个传感器输出电压的阶跃幅值,其具体数值可通过数据采集系统测试获得。式(7)中的矩阵U可写为
(9)
将式(3)、式(8)和式(9)代入式(7),可获得SMTP的标定矩阵W,它是一个6行8列的常数矩阵。当被测活动部件安装在SMTP上工作时,通过数据采集系统可测得SMTP的输出电压U(t),则活动部件6分量的扰振力/力矩为
F6×1(t)=W6×8U8×1(t)
(10)
2.2PMTP标定方法
PMTP的标定过程是在频域上完成的,它是通过力锤敲击对标定装置施加已知的冲激载荷来实现的。冲击载荷的傅里叶变换是一个宽频激励[16]。图8为力锤敲击冲激载荷的傅里叶变换形式。
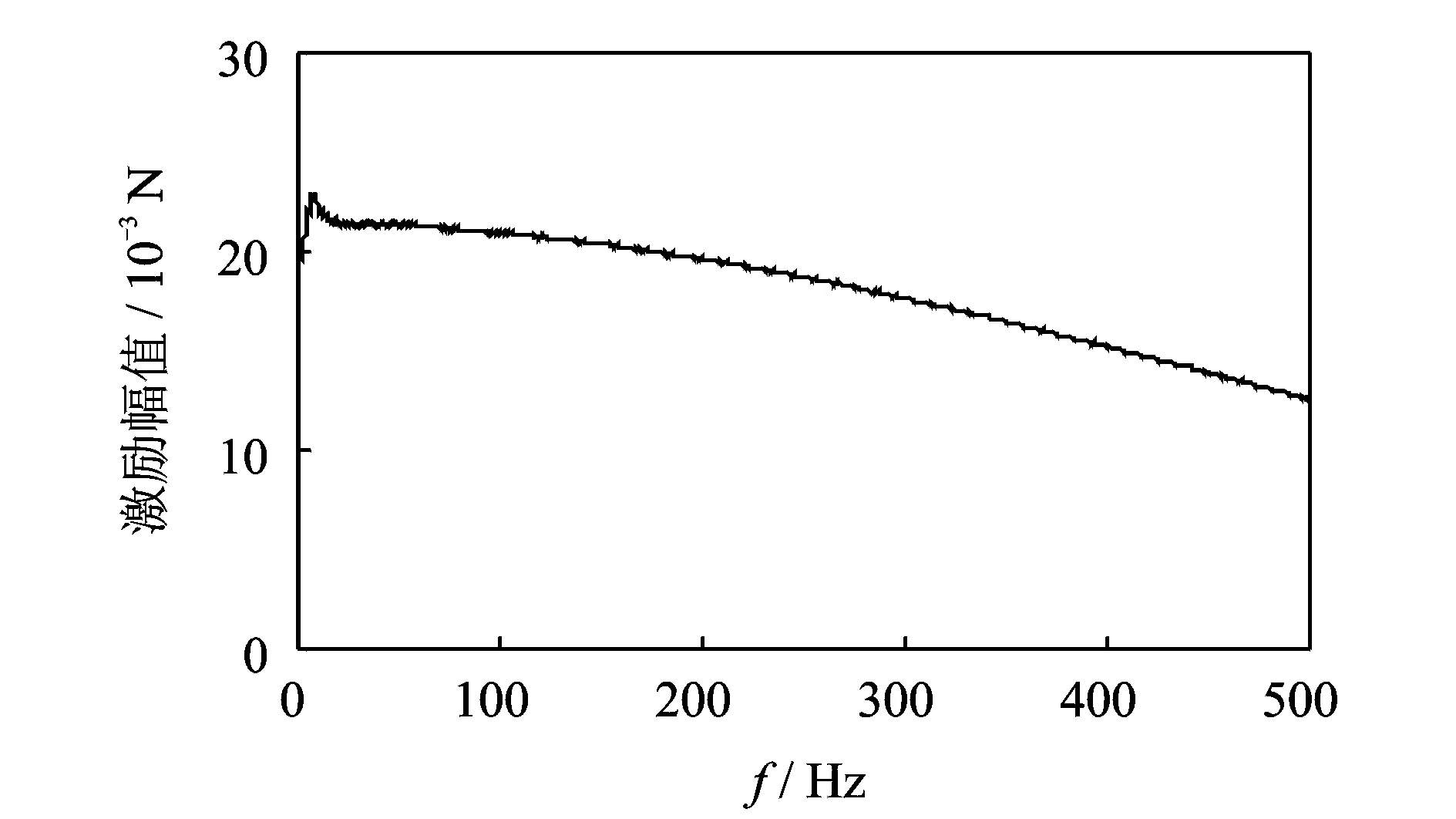
图8 冲激载荷的傅里叶变换Fig.8 Fourier transform of impulse force
在标定过程中,利用数据采集系统对12个已知冲激载荷的频域信号和PMTP输出电压的频域信号进行测试。式(7)中的矩阵F′和U分别为
其中:ω为角频率。
将式(3)、式(11)和式(12)代入式(7),获得PMTP的标定矩阵W(ω),它在每个频点处均为一个6行8列的矩阵。当被测活动部件安装在PMTP上工作时,通过数据采集系统可测得PMTP输出电压的频域信号U(ω),则活动部件6分量的扰振力/力矩为
F6×1(ω)=W6×8(ω)U8×1(ω)
(13)
3 测试误差
由图6和式(3)可知,对标定装置的加载点2,4和9施加单向已知力时,简化至等效中心点O可分别等效出Fy,Mx和Mz分量;Fx,My和Mz分量以及Fz,Mx和My分量。因此在获得了测试平台的标定矩阵后,分别对标定装置的加载点2,4和9再次施加单向已知力,通过对比已知激励和测试结果可获得测试平台的测试误差。
3.1SMTP测试误差
在获得了SMTP的标定矩阵后,使用图7所示的加载装置再次对标定装置的加载点2,4和9施加阶跃载荷。由于砝码及其附属装置的质量m为2.06 kg,则阶跃载荷的阶跃幅值为
G=mg=2.06×9.8=20.188 N
(14)
表1为3个已知的阶跃载荷简化至等效中心点O处的6分量力/力矩结果。
图9~11分别为对标定装置的加载点2,4和9施加阶跃载荷时,SMTP对6分量力/力矩的测试结果。

表1 阶跃载荷简化结果
对比表1和图9~图11可知,SMTP可对6分量力/力矩实现高精度地测试。表2为SMTP对6分量力/力矩的测试误差。由表2可知,SMTP对6分量力/力矩的测试误差在±1.10%以内。

表2 SMTP测试误差

图9 加载点2施加阶跃载荷时SMTP测试结果Fig.9 Testing results of SMTP under the action of step force acting on loading point No.2

图10 加载点4施加阶跃载荷时SMTP测试结果Fig.10 Testing results of SMTP under the action of step force acting on loading point No.4
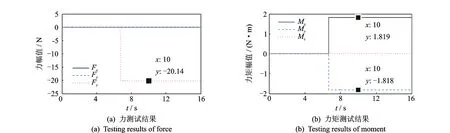
图11 加载点9施加阶跃载荷时SMTP测试结果Fig.11 Testing results of SMTP under the action of step force acting on loading point No.9
3.2 PMTP测试误差
在获得了PMTP的标定矩阵后,使用力锤再次对标定装置的加载点2,4和9施加宽频激励,并将3个宽频激励简化至等效中心点O。笔者选取加载点2处的Fy分量,加载点4处的Fx和Mz分量以及加载点9处的Fz,Mx和My分量,通过对比选取6个分量的简化结果和测试结果来检验PMTP对6分量力/力矩的测试误差。图12为选取的6个分量的简化结果与测试结果的对比图。由图12可知,6个分量的简化结果与测试结果吻合程度良好,即PMTP可对6分量力/力矩实现高精度测试。不考虑PMTP的低频性能,表3为PMTP在10~500 Hz的范围内对6分量力/力矩在不同频点处测试误差的最大值。由表3可知,PMTP对6分量力/力矩的测试误差在±4.94%以内。
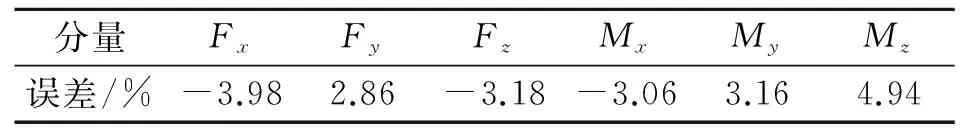
表3 PMTP测试误差最大值

图12 6个分量简化结果与测试结果的对比图Fig.12 Comparative results of simplified results and testing results of 6-component force/moment
4 工作性能
为了进一步检验两种测试平台的工作性能,分别利用SMTP和PMTP对太阳翼驱动机构(solar array drive assembly,简称SADA)驱动同一刚性负载运行时的扰振力矩Mz进行测试。在测试过程中,设计了一套重力卸载装置,它由卸载支架和气浮轴承组成,其工作原理为:通过气浮轴承和卸载支架将刚性负载的重力传递到地面上,使刚性负载对SADA只有转动惯量的作用,与SADA在轨的工作条件一致,消除了负载重力对测试结果的影响。图13为测试设备照片。
图14为SMTP和PMTP对SADA驱动同一刚性负载运行时扰振力矩Mz的测试结果。由图14可知,SMTP和PMTP对扰振频率(处于中频区)的测试结果一致,但二者对同一扰振频率处扰振幅值的测试结果存在偏差。表4为SMTP和PMTP对同一扰振频率处扰振幅值的测试误差。由表4可知,SMTP和PMTP对同一微振动振动幅值的测试误差在±4.36%以内。

图13 测试设备照片Fig.13 Pictures of testing equipment
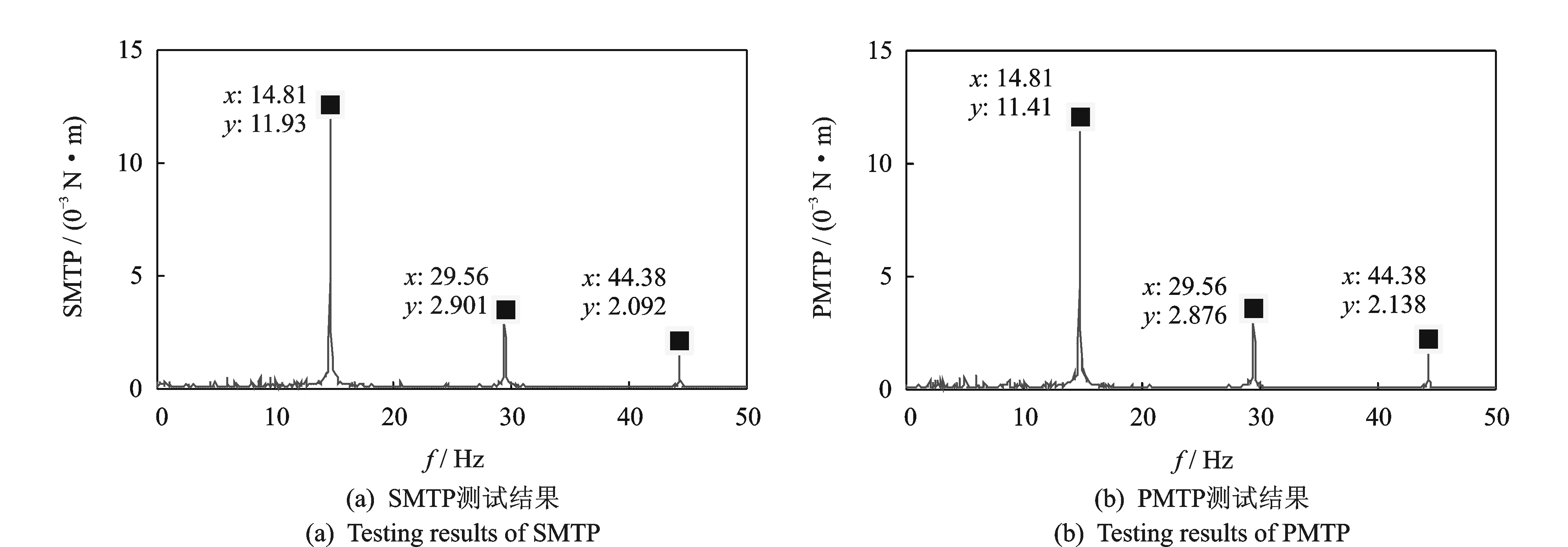
图14 SADA驱动刚性负载扰振力矩的测试结果Fig.14 Testing results of SADA disturbance torque driving a rigid load
表4 扰振幅值的测试误差
Tab.4 Testing errors of disturbance amplitude
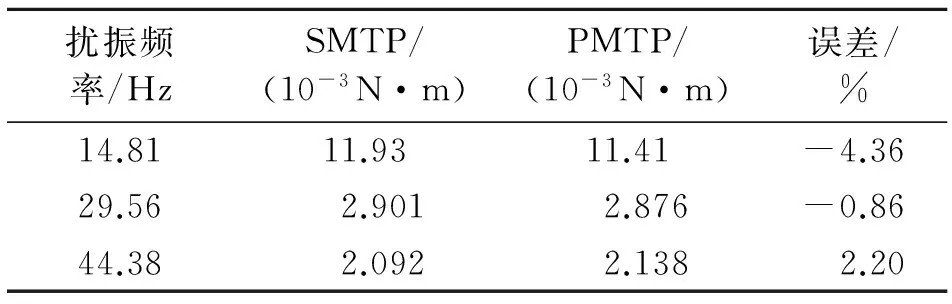
扰振频率/HzSMTP/(10-3N·m)PMTP/(10-3N·m)误差/%14.8111.9311.41-4.3629.562.9012.876-0.8644.382.0922.1382.20
5 结束语
研制了应变式和压电式两种微振动测试平台(SMTP和PMTP),并分别针对两种测试平台开发了高精度的标定方法。通过试验测试对两种测试平台的测试误差进行检验,结果表明:SMTP和PMTP对6分量力/力矩的测试误差分别在±1.10%和±4.94%以内。为了进一步检验两种测试平台的工作性能,分别利用SMTP和PMTP对SADA驱动同一刚性负载运行时的扰振力矩进行测试,结果表明:二者对同一微振动扰振频率的测试结果一致,对扰振幅值的测试误差在±4.36%以内。该结论为航天器活动部件微振动特性的地面测试试验奠定了基础。
[1] Kamesh D, Pandiyan R, Ghosal A. Modeling, design and analysis of low frequency platform for attenuating micro-vibration in spacecraft[J]. Journal of Sound and Vibration, 2010,329(17):3431-3450.
[2] 张鹏飞, 程伟, 赵煜. 考虑耦合效应的动量轮扰动测量[J]. 北京航空航天大学学报, 2011,37(8):948-952.
Zhang Pengfei, Cheng Wei, Zhao Yu. Measure of reaction wheels disturbance considering coupling effect[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011,37(8):948-952. (in Chinese)
[3] 徐赵东,翁沉卉,朱俊涛.航天器中反作用轮干扰力仿真研究[J].振动、测试与诊断,2013,33(5):881-885.
Xu Zhaodong, Weng Chenhui, Zhu Juntao. Method for reaction wheel assembly simulation on spacecraft[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(5):881-885. (in Chinese)
[4] Chen Jiangpan, Cheng Wei, Han Wei. Analysis and simulation of stepper motor disturbance considering structural coupling[J]. Applied Mechanics and Materials, 2014,526:103-108.
[5] Chen Jiangpan, Cheng Wei, Wang Yunfeng. Modeling and simulation of solar array drive assembly disturbance driving a flexible load[J]. Applied Mechanics and Materials, 2014,565:67-73.
[6] 程啟华, 李永新. 压电传感器低频动态补偿数字滤波器设计[J]. 电子测量技术, 2007,30(8):143-146.
Cheng Qihua, Li Yongxin. Design for low-frequency compensation of piezoelectric sensor based on digital filter[J]. Electronic Measurement Technology, 2007,30(8):143-146. (in Chinese)
[7] Masterson R A. Development and validation of empirical and analytical reaction wheel disturbance models[D]. Boston: Massachusetts Institute of Technology, 1999.
[8] Masterson R A, Miller D W, Grogan R L. Development and validation of reaction wheel disturbance models: empirical model[J]. Journal of Sound and Vibration, 2002,249(3):575-598.
[9] Kamesh D, Pandiyan R, Ghosal A. Passive vibration isolation of reaction wheel disturbances using a low frequency flexible space platform[J]. Journal of Sound and Vibration, 2012,331(6):1310-1330.
[10]Zhou Weiyong, Li Dongxu, Luo Qing, et al. Analysis and testing of microvibrations produced by momentum wheel assemblies[J]. Chinese Journal of Aeronautics, 2012,25(4):640-649.
[11]Luo Qing, Li Dongxu, Zhou Weiyong, et al. Dynamic modelling and observation of micro-vibrations generated by a single gimbal control moment gyro[J]. Journal of Sound and Vibration, 2013,332(19):4496-4516.
[12]Zhou Weiyong, Li Dongxu. Experimental research on a vibration isolation platform for momentum wheel assembly[J]. Journal of Sound and Vibration, 2013,332(5):1157-1171.
[13]何芝仙, 常小强, 李震. 双孔平行梁式传感器设计的理论分析与实验研究[J]. 试验技术与试验机, 2006,46(1):14-17.
He Zhixian, Chang Xiaoqiang, Li Zhen. Theoretical analysis and experimental research on the beam sensor with two parallel holes[J]. Test Technology and the Testing Machine, 2006,46(1):14-17. (in Chinese)
[14]谢永华, 孟凡虎. 双孔平行梁式称重传感器非线性校正研究[J]. 现代科学仪器, 2010(6):64-66.
Xie Yonghua, Meng Fanhu. Nonlinear correction study of double parallel beam weighing transducer[J]. Modern Scientific Instruments, 2010(6):64-66. (in Chinese)
[15]陈江攀, 程伟, 夏明一. 一种应变式超低频微振动测试台[J]. 振动与冲击, 2014,33(24):77-81.
Chen Jiangpan, Cheng Wei, Xia Mingyi. An ultra-low frequency micro-vibration testing platform based on strain-resistance effect[J]. Journal of Vibration and Shock, 2014,33(24):77-81. (in Chinese)
[16]宋爱国, 刘文波, 王爱民. 测试信号分析与处理[M]. 北京: 机械工业出版社, 2007:21-30.

10.16450/j.cnki.issn.1004-6801.2017.01.013
*航天国防科研资助项目
2015-03-16;
2015-07-02
TH823; V416
陈江攀,男,1988年4月生,博士生。主要研究方向为航天器活动部件的微振动特性、微振动信号测试与处理及结构动力学。曾发表《一种应变式超低频微振动测试台》(《振动与冲击》2014年第33卷第24期)等论文。 E-mail:chenjiangpan@hotmail.com

